УДК 51
Лекция
ГРУППЫ И СИММЕТРИИ
© 1996 г. Е. П. Емельченков, Р. Е. Кристалинский
Математика двадцать первого века может сильно отличаться от нашей;
возможно школьник начнет изучение алгебры с теории групп подстановок,
что он мог бы сделать и сейчас, если бы не установившиеся традиции.
Саймон Ньюкомб, 1893
Три источника теории групп
Не следует думать, что определение группы целиком и полностью сложилось в уме какого-то одного математика. Понадобилась работа нескольких поколений математиков, занявшая в общей сложности около 100 лет, прежде чем идея группы сформировалась с ее сегодняшней ясностью. Истоки понятия группы обнаруживаются в трех дисциплинах: теории решения алгебраических уравнений; геометрии и теории чисел.
Основной задачей алгебры до XIX века было решение алгебра-ических уравнений. После того как в эпоху Возрождения были найдены формулы для решения уравнений третьей и четвертой степени, математики приложили много усилий к отысканию аналогичных формул для решения уравнений пятой степени и выше. Однако работа в этом направлении в течении нескольких столетий не давала положительных результатов. Это поставило перед математикой вопрос: существуют ли вообще такие формулы?
В 1771 году Ж. Лагранж и А. Вандермонд заметили, что вопрос о разрешимости каждого уравнения сводится к изучению подстановок из его корней. Затем в ряде работ П. Руффини (в 1799 году и позднее), посвященных разрешимости уравнения 5-й степени в радикалах, по существу описал группу подстановок из пяти символов. В 1824 году норвежский математик Н. Х. Абель доказал теорему: ни для какого n>5 нельзя указать формулу, которая выражала бы корни любого алгебраического уравнения n-й степени через его коэффициенты при помощи радикалов (т.е. при помощи действий сложения, вычитания, умножения, деления и извлечения корня с целым показателем степени). Доказательство теоремы основывалось на глубоких связях между свойствами групп подстановок и свойствами корней алгебраических уравнений. Общее исследование проблем разрешимости алгебраических уравнений в радикалах было выполнено французским математиком Э. Галуа в 1830 году. В теории Галуа уже достаточно сознательно использовалась идея группы, им же впервые был введен и сам термин "группа".
Независимо и из других соображений идея группы возникла в геометрии, когда в середине XIX века на смену единой античной геометрии пришли многочисленные "геометрии" и остро встал вопрос об установлении связей и родства между ними. Выход из создавшегося положения был намечен исследованиями по проективной геометрии, посвященными изучению поведения фигур при различных преобразованиях. Постепенно интерес в этих исследованиях перешел на изучение самих преобразований и поиск их классификации. Таким "изучением геометрического родства" много занимался А. Мебиус. На более сознательном уровне классификацию геометрий дал А. Кэли (1854), он явно пользовался термином "группа", систематически использовал таблицы умножения, ныне называемые таблицами Кэли, и доказал представимость всякой конечной группы подстановками. Заключительным этапом на этом пути явилась "Эрлангенская программа" Ф. Клейна (1872), положившая в основу классификации геометрий понятие группы преобразований: каждая геометрия определяется некоторой группой преобразований пространства, и только те свойства фигур принадлежат к данной геометрии, которые инвариантны относительно преобразований соответствующей группы.
Третий источник понятия группы - теория чисел. Здесь основные на: Л. Эйлер, изучавший "вычеты, остающиеся при делении степеней" (1761), К. Гаусс с его "композицией двоичных квадратичных форм" (1801) и Кронекер, по существу описавший конечные абелевы группы на языке теории чисел (1870).
Осознание в конце XIX века принципиального единства теоретико-групповых идей, существовавших к тому времени независимо в разных областях математики, привело к выработке современного абстрактного понятия группы (С. Ли, Г. Фробениус и др.). Это был один из самых ранних примеров абстрактной алгебраической системы. Он послужил во многих отношениях образцом при перестройке других областей алгебры и всей математики на рубеже XX века - их путь уже не был столь извилистым и трудным. Изучение групп без предположения их конечности и без каких бы то ни было предположений о природе элементов впервые оформилось в самостоятельную область математики с выходом в 1916 году книги О. Ю. Шмидта "Абстрактная теория групп".
Прежде чем дать определение группы,
сформулируем определение бинарной
алгебраической операции.
Определение 1. Бинарной алгебраической
операцией, заданной на множестве M, называется
отображение *, сопоставляющее каждой
упорядоченной паре элементов a и b из M некоторый
элемент с из M, называемый композицией элементов a
и b. Для обозначения композиции элементов a и b
используется запись a * b.
Пример 1. Операция сложения (+) на множестве N
натуральных чисел является бинарной
алгебраической операцией.
Пример 2. Операция вычитания (-) на множестве N
натуральных чисел не является бинарной
алгебраической операцией, так как результат
вычитания двух натуральных чисел не всегда
принадлежит множеству N. Однако на множестве Z
целых чисел операция вычитания является
бинарной алгебраической операцией.
Пример 3. Операция деления (:) на множестве
действительных чисел не всегда выполнима,
поэтому деление не является бинарной
алгебраической операцией на R. В то же время на
множестве R \ {0} действительных чисел без нуля
операция деления является бинарной
алгебраической операцией.
Определение 2. Бинарная алгебраическая
операция *, определенная на множестве M,
называется ассоциативной, если для любых
элементов a, b, c из множества M выполняется
равенство:
(a * b) * c = a * (b * c)
Пример 4. Операция сложения на
множестве R действительных чисел является
ассоциативной.
Пример 5. Операция вычитания на множестве R
действительных чисел ассоциативной не является,
так как, например:
(9 - 4) - 3 9 - (4 - 3)
Свойство ассоциативности позволяет
однозначным образом определить композицию для
любого конечного числа элементов множества M, то
есть позволяет доказать независимость
композиции любых n элементов от расстановки
скобок. Например:
4 * ((5 * 2) * 3) = (4 * 5) * (2 * 3)
Определение 3. Бинарная
алгебраическая операция *, опреде-ленная на
множестве M, называется коммутативной, если для
любых элементов a, b из множества M выполняется
равенство:
a * b = b * a
Пример 6. Операция сложения на
множестве R действительных чисел является
коммутативной.
Пример 7. Операция вычитания на
множестве R действительных чисел коммутативной
не является, так как, например:
9 - 4 4 -
9
Определение 4. Множество G вместе с
определенной на нем бинарной алгебраической
операцией * называется группоидом. Группоид G с
операцией * будем обозначать <G; *>. Множество G
при этом называется носителем группоида.
Сформулируем теперь формальное
определение группы.
Определение 5. Множество G с
заданной на нем бинарной алгебраической
операцией * называется группой, если выполняются
условия:
1) операция * ассоциативна;
2) в G существует такой элемент e (называемый нейтральным элементом), что для любого элемента a из G
a * e = e * a = a;
3) для любого элемента a из G существует такой элемент a' (называемый симметричным к элементу a), что
a * a' = a' * a = e.
Замечание 1. Если в группе операция * обозначается знаком "·" или знаком "x", то говорят о мультипликативной записи операции. При этом нейтральный элемент обозначают 1 и называют единицей, а симметричный элементу a обозначают a-1 и называют обратным.
Если в группе операция * обозначается
знаком +, то говорят об аддитивной записи
операции. При этом нейтральный элемент
обозначают 0 и называют нулем, а симметричный
элементу a обозначают a-1 и называют противоположным.
Пример 8. Множество целых чисел относительно
операции сложения <Z; +> образует группу.
Пример 9. Множество положительных
действительных чисел относительно операции
умножения <R+; x> образует группу.
Пример 11. Множество {1, -1}, состоящее из целых
чисел 1 и -1 относительно операции умножения также
образует группу.
Пример 12 (группа переключателей). Назовем
переключателем электрическую схему, имеющую три
входа и три выхода, соединенные попарно в
некотором порядке. Таких переключателей всего
шесть (рис.1).
Рис. 1. Шесть переключателей
На множестве переключателей определим операцию * соединения переключателей. Например, в результате соединения переключателей П2 и П4 (рис. 2) вход 1 будет соединен с выходом 3, вход 2 - с выходом 2, вход 3 - с выходом 1. Точно такое же соответствие между входами и выходами осуществляет переключатель П5. Поэтому можно записать
П2 * П4 = П5.
Рис.2. Результат соединения
двух переключателей
Из определения операции соединения переключателей следует, что на множестве переключателей эта операция является бинарной алгебраической. Очевидно также, что операция соединения перек-лючателей ассоциативна. Нейтральным элементом во множестве переключателей является переключатель П1.
Результаты различных соединений
переключателей удобно собрать в одну квадратную
таблицу (рис. 3), в которой слева стоят левые
переключатели, сверху - правые, а на пересечении
соответствующих строк и столбцов - их соединения.
| П1 | П2 | П3 | П4 | П5 | П6 |
|
| П1 | П1 | П2 | П3 | П4 | П5 | П6 |
| П2 | П2 | П1 | П4 | П3 | П6 | П5 |
| П3 | П3 | П5 | П1 | П6 | П2 | П4 |
| П4 | П4 | П6 | П2 | П5 | П1 | П3 |
| П5 | П5 | П3 | П6 | П1 | П4 | П2 |
| П6 | П6 | П4 | П5 | П2 | П3 | П1 |
Рис.
3. Таблица соединений переключателей
Из таблицы соединений на рисунке 3
определяем, что
П1 * П1 = П1, П2 * П2 = П1, П3 * П3 = П1,
П6 * П6 = П1, П4
* П5 = П5 * П4 = П1.
Следовательно, для каждого
переключателя П существует симмет-ричный ему
переключатель П':
П1' = П1, П2' = П2, П3' = П3, П4' = П5, П5' = П4, П6' = П6.
Таким образом, множество переключателей
относительно опера-ции соединения
переключателей образует группу.
Определение 6. Группа с коммутативной
бинарной алгебраической операцией называется абелевой
группой.
Все приведенные выше примеры групп, кроме группы
переключа-телей, являются абелевыми группами.
Группа переключателей абелевой
не является, так как, например,
П3 * П4 = П6, П4
* П3 = П2 (рис. 4).
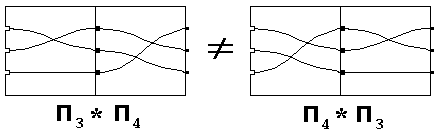
Рис. 4. Соединение двух пар
переключателей
Рассмотрим одну занимательную задачу,
связанную со свойствами бинарных алгебраических
операций.
Пример 13. Задача о наследовании признака.
Пусть имеется конечное множество M простейших
существ, каждое из которых обладает одним из
признаков A, B, C. Пусть, например, эти признаки
характеризуют форму глаз соответственно
круглые, квадратные и треугольные. Известно, что
в результате слияния двух существ X и Y получается
одно новое существо Z. При этом наследование
формы глаз осуществляется по закону * описанному
таблицей на рисунке 5.
Рис. 5. Таблица для операции
наследования
В результате эволюции существ остается одно существо. Требуется доказать, что форма глаз оставшегося существа не зависит от того, в каком порядке сливаются существа.
Из таблицы на рисунке 5 видно, что операция слияния признаков существ ассоциативна и коммутативна. Поэтому наследуемый признак результата слияния всех существ с признаками s1, s2, ... , s3 не зависит от порядка их попарного слияния и совпадает с композицией s1*s2*...*s3.
Например, если в исходном множестве содержатся существа с признаками a, b, c, d и слияние существ происходит в следующем порядке: сначала сливаются a и d, затем b и c и, наконец, оставшиеся два существа, то признак результата слияния существ выражается формулой:
(a*d)*(b*c) = a*(d*(b*c)) = a*((b*c)*d) = (a*(b*c))*d = ((a*b)*c)*d = a*b*c*d.
Так, если в исходном множестве содержатся два существа с треугольными глазами и по одному существу с квадратными и круглыми глазами, то в результате эволюции останется существо с треугольными глазами.
Пусть каждому элементу x некоторого
множества X ставится в соответствие по
определенному правилу элемент y множества Y;
тогда говорят, что задано отображение
множества X в множество Y. Элемент y называют образом
элемента x, а элемент x - прообразом элемента y.
Зависимость между образом и его прообразом
выражают следующей записью:
y = (x),
где обозначает данное отображение.
На рисунке 6 дано стрелочное представление некоторого отображения a из множества X = {x1, x2, x3, x4, x5} во множество Y = {y1, y2, y3, y4}.
Рис. 6. Стрелочное
представление отображения
Если при отображении каждый элемент множества Y является образом хотя бы одного элемента множества X, то называют отображением множества X на множество Y или (сюръекцией X на Y). На рисунке 7 приведен пример отображения множества X на множество Y.
Рис. 7. Отображение множества X
на множество Y
Отображение множества X на множество Y называется взаимно однозначным (или биекцией множества X на множество Y), если для каждого элемента множества Y во множестве X найдется ровно один прообраз.
Таким образом, если - биекция множества X на множество Y, то для
любых элементов y1 и y2 из множества Y
(y1)
=
(y2) => y1 = y2.
При стрелочном представлении отображения это означает, что на рисунке отсутствуют точки, в которых сходятся две или более стрелок.
На рисунке 8 приведен пример взаимно
однозначного отображения множества X на
множество Y.
Рис. 8. Взаимно однозначное
отображение
Для всякого взаимно однозначного
отображения множества X на множество Y существует
обратное отображение множества Y на
множество X. Обратное отображение определяется
тем, что каждому элементу y множества Y ставится в
соответствие его прообраз x из множества X. Если
исходное отображение обозначается буквой , то обратное отображение
обозначают символом
-1
и пишут
x = -1(y).
Очевидно, обратное отображение также является взаимно однозначным.
Взаимно однозначное отображение множества на себя называется преобразованием этого множества.
Два преобразования и
одного и того
же множества M называются равными, если они
одинаково действуют на элементы множества M, то
есть для любого элемента x из множества M
(x) =
(x).
Определим теперь композицию
(произведение) двух отображений. Пусть - отображение множества X
во множество Y и
-
отображение множества Y во множество Z.
Последовательное выполнение отображений
и
, сопоставляющее каждому элементу x из
множества X некоторый элемент z из множества Z по
закону z =
(
(x)) (рис. 9), является
отображением множества X во множество Z. Это
отображение называется композицией отображений
и
и обозначается
.
Рис. 9. Стрелочное
представление композиции отображений
Очевидно, если и
являются
преобразованиями множества M, то и их композиция
также является
преобразованием множества M. Таким образом,
композиция двух преобразований множества M
является бинарной алгебраической операцией на
совокупности всех преобразований заданного
множества M.
Выясним теперь свойства композиции преобразований. Оказывается, совокупность всех преобразований фиксированного множества M относительно композиции преобразований образует группу.
Докажем сначала, что операция
композиции преобразований ассоциативна. Пусть x -
произвольный элемент множества M и ,
,
- преобразования этого
множества и пусть
(x) = x1,
(x) = x2,
(x2) = x3,
тогда
(x) =
x2,
(x1) = x3,
следовательно,
(
)(x)
=
(x2) = x3, (
)
(x) =
(x1) = x3.
Поэтому для любого элемента x из
множества M
(
)(x)
= (
)
(x) (рис. 10),
Таким образом, по определению
равенства преобразований
(
)
= (
)
.
Рис. 10. Ассоциативность
произведения преобразований
Нейтральным элементом во множестве преобразований служит тождественно преобразование e, переводящее каждый элемент x из M в себя:
(x) = x.
Докажем это. Пусть
(x) = x1,
тогда
(x)
=
(x1) = x1 =
(x) =
(
(x)) =
(x).
Поэтому
=
=
,
то есть
является нейтральным элементом относительно
композиции преобразований.
Симметричным элементом для
преобразования
является обратное преобразование
-1.
Действительно, если (x) = x1, то
-1
(x) =
-1(x1) = x =
(x)
и
-1(x1)
=
(x) = x1 =
(x1).
Следовательно,
-1
=
-1 =
,
что и требовалось доказать. Таким образом, совокупность всех преобразований множества M относительно композиции преобразований образует группу.
Группа всех преобразований
произвольного множества M не является абелевой.
Для того, чтобы это доказать, достаточно указать
хотя бы два преобразования и
множества M и
хотя бы один элемент x из M, на который
преобразования
и
действуют по
разному. Пусть, например,
и
- два
преобразования множества M = {a, b, c}, стрелочные
представления которых приведены на рисунке 11.

Рис. 11. Два преобразования
Тогда
(b)
=
(c) = b и
(b) =
(c) = a,
поэтому
.
Группа подстановок
Определение 7. Преобразования конечного множества M называ-ются подстановками множества M. Если множество M содержит n элементов, то группа преобразований множества M называется груп-пой подстановок n-й степени или симметрической группой n-й степени и обозначается Sn.
Пример 14. Рассмотрим
симметрическую группу 3-ей степени множества M = {a,
b, c}. Число подстановок множества M равно шести.
Подстановки удобно описывать с помощью
специальных схем, в которых под каждым элементом
указывается его образ. На рисунке 12 перечислены
все подстановки симметрической группы S3.
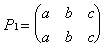
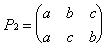
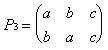
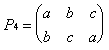
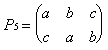
Рис. 12. Подстановки
симметрической группы S3
Здесь, например, подстановка
это преобразование множества M такое,
что a b, b
a, c
c.
Схемы, отличающиеся только порядком
столбцов, определяют одну и ту же подстановку и
поэтому не считаются различными, например:
При таком представлении подстановок
легко находится их произведение (следует только
помнить, что сначала выполняется правый
сомножитель, затем левый):
При таком определении умножения подстановок роль единицы выполняет тождественная подстановка P1. Для нахождения обратной подстановки достаточно переставить местами верхнюю и нижнюю строки подстановки, например:
Произведение подстановок удобно представлять с помощью квадратной таблицы (рис. 13), в которой слева стоят левые множители, сверху - правые, а на пересечении соответствующих строк и столбцов - их произведения.
P1 |
P2 |
P3 |
P4 |
P5 |
P6 | |
P1 |
P1 |
P2 |
P3 |
P4 |
P5 |
P6 |
P2 |
P2 |
P1 |
P5 |
P6 |
P3 |
P4 |
P3 |
P3 |
P4 |
P1 |
P2 |
P6 |
P5 |
P4 |
P4 |
P3 |
P6 |
P5 |
P1 |
P2 |
P5 |
P5 |
P6 |
P2 |
P1 |
P4 |
P3 |
P6 |
P6 |
P5 |
P4 |
P3 |
P2 |
P1 |
Рис. 13. Таблица Кэли симметрической
группы S3
Таблицы такого рода можно составить для любой конечной группы, их называют таблицами Кэли.
Таблицы Кэли являются удобным способом
представления груп-овых операций для конечных
групп. Этими таблицами довольно легко
пользоваться. Например, чтобы найти по таблице
группы S3 (рис. 13) обратную данной
подстановке, надо в строчке, отмеченной слева
данной подстановкой, найти нейтральный элемент P1;
в заголовке столбца, в котором находится этот
элемент, и стоит подстановка симметричная
данной. Как легко видеть, для группы S3
имеем:
P1-1 = P1, P2-1
= P2, P3-1 = P3, P4-1 =
P5, P5-1 = P4, P6-1 = P6.
Элементами множества M, на котором выполняются подстановки, могут быть любые предметы, а не только буквы a, b, c. В таком смысле можно говорить о подстановках любых предметов. Так как при этом природа предметов значения не имеет, то эти предметы обычно обозначаются числами, и речь идет о подстановках чисел.
Естественно возникает вопрос: нельзя ли получить группу, взяв не все, а только некоторые из элементов группы и сохранив для них ту же алгебраическую операцию? Нетрудно убедиться, что ответ на этот вопрос утвердительный.
В самом деле, рассмотрим, например, подмножество {P1, P2} симметрической группы S3. Для этого множества таблица Кэли выглядит так, как показано на рисунке 14.
П1 |
П2 |
|
П1 |
П1 |
П2 |
П2 |
П2 |
P1 |
Рис. 14. Таблица Кэли
Очевидно, операция, соответствующая
приведенной таблице, является бинарной
алгебраической операцией на множестве {P1, P2}.
Нетрудно также проверить, что все групповые
аксиомы выполнены. Следовательно, группоид <{P1,
P2}; > является
группой.
Точно также можно убедиться, что подмножество {P1, P3} в свою очередь образует группу, как и подмножество {P1, P6}.
Что же касается подмножества {P1, P5},
то оно подгруппы не образует, так как P5P5 = P4. Эти простые
рассуждения оправдывают введение следующего
общего определения.
Определение. Пусть задана какая-нибудь
группа <G; *>; тогда, если множество H, состоящее
из некоторых элементов множества G, образует
группу относительно операции *, то группа <H; *>
называется подгруппой группы <G; *>.
Таким образом, структуры <{P1, P3}; > и <{P1, P6};
> являются подгруппами
симметрической группы S3.
Теорема (критерий подгруппы). Непустое
подмножество H группы G = <G; *> образует
подгруппу группы G, тогда и только тогда, когда:
1) для любых двух элементов a, b из H их композиция a * b принадлежит H;
2) для любого элемента a из H
симметричный ему элемент a' также принадлежит H.
Действительно, условие 1 означает что операция *
будет также бинарной алгебраической операцией
на множестве H. Это условие также называется
условием замкнутости множества H относительно
данной операции. Ассоциативность операции * на H
вытекает из ее ассоциативности на G. Наконец, из
условий 1 и 2 следует, что Н содержит нейтральный
элемент e: взяв какой-нибудь элемент a из H, по
условию 2 мы найдем в H симметричный ему элемент a',
а по условию 1 получим, что нейтральный элемент e =
a * a' также содержится в H.
Воспользовавшись критерием подгруппы, нетрудно
проверить, что множество {P1, P4, P5}
является подгруппой (порядка 3) симметрической
группы S3. Таблица Кэли для этой подгруппы
приведена на рисунке 15. Эта таблица легко
получается из таблицы Кэли группы S3 (рис. 13)
удалением лишних строк и столбцов.
П1 |
П4 |
П5 |
|
П1 |
П1 |
П4 |
П5 |
П4 |
П4 |
П5 |
П1 |
П5 |
П5 |
П1 |
П4 |
Рис. 15. Таблица Кэли для подгруппы
порядка 3
Других подгрупп порядка 3 в симметрической
группе S3 нет. Читателю предлагается самому
убедиться в этом. Подгрупп порядка 4 и 5 в группе S3
не имеется вовсе.
Итак, симметрическая группа S3
имеет всего три подгруппы порядка 2 <{P1, P2};
>, <{P1, P3};
> и <{P1, P6};
>, одну подгруппу порядка
3 <{P1, P4, P5};
> и две тривиальных подгруппы порядка 1
<{P1;
> и порядка
6 <{P1, P2, P3, P4, P5, P6};
>.
Интересно отметить, что все нетривиальные
подгруппы симметрической группы S3
оказались абелевыми, хотя сама группа S3
таковой не является.
Определение 9. Пусть G1 = <G1;
*> и G2 = <G2; > - два группоида. Гомоморфизмом
группоида G1 на группоид G2 называется
сюръекция
: G1
G2 множества G1
на множество G2, сохраняющая групповую
операцию:
(a * b) =
(a)
(b).
Если для группоидов G1 и G2
такая сюръекция существует, то говорят, что
группоид G1 гомоморфно отображается на
группоид G2.
Изоморфизмом группоида G1 на
группоид G2 называется биекция : G1
G2 множества G1 на
множество G2, сохраняющая групповую
операцию:
(a * b) =
(a)
(b).
Если между двумя группоидами G1 и
G2 можно установить изоморфизм, то
группоиды G1 и G2 называют
изоморфными. Факт изоморфизма группоидов G1
и G2 обозначают: G1 G2.
Так как группа является группоидом, то можно
говорить и о гомоморфизме и изоморфизме групп.
Пример 15. Пусть G1 = <Z; +> и G2
= <{1, -1}; > - две группы.
Отображение
,
сопоставляющее каждому целому четному числу
число 1, а каждому целому нечетному числу - число
-1, является гомоморфизмом группы G1 на
группу G2.
Пример 16. Пусть G1 = <Z; +> -
аддитивная группа целых чисел, G2 = <{5k | k
Z}; +> - аддитивная группа целых чисел,
кратных 5. Отображение
(a) = 5
a является
изоморфизмом группы G1 на группу G2.
Пример 17. Аддитивная группа действительных
чисел <R; +> изоморфна мультипликативной группе
положительных действительных чисел <R+; >. Изоморфизм этих групп
устанавливается, например, биекцией
(a) = 2a. Действительно,
(a + b) =
2a+b = 2a
2b
=
(a)
(b).
Этот пример показывает, что между
группами можно установить иногда несколько
изоморфизмов (в данном случае бесконечно много,
так как для любого положительного отличного от 1
числа x отображение (a) =
xa устанавливает изоморфизм между
группами).
Изоморфные группы отличаются друг от друга по
сути дела лишь обозначениями и с точки зрения
теории групп считаются одинаковыми.
Пусть G1 = <G1; *> -
группа, G2 = <G2; > - группоид и существует гомоморфизм
группы G1 на
группу G2. Возникает вопрос: какие
свойства операции * группы G1 переносятся
на операцию
группы G2?
Ответ на этот вопрос содержится в следующей
теореме.
Теорема 2. Если группа G1 = <G1;
*> гомоморфно отображается на группоид G2
= <G2; >, то
группоид G2 является группой.
Доказательство. Пусть -
гомоморфизм группы G1 на группоид G2.
Рассмотрим три элемента a2, b2, c2
из множества G2. Так как
- сюръекция, то во множестве G1
существуют прообразы этих элементов a1, b1,
c1: a2 =
(a1),
b2 =
(b1), c2
=
(c1). Так как для
элементов a2, b2, c2 выполняется
равенство:
(a2b2)
c2 = (
(a1)
(b1))
(c1) =
(a1*b1)
(c1) =
(a1*b1)*c1)=
=
(a1*(b1*c1))
=
(a1)
(b1*c1)
=
(a1)
(
(b1)
(c1))
= a2
(b2
c2),
то операция в
группоиде G2 ассоциативна.
Элемент (e1)
= e2 (образ нейтрального элемента группы G1)
является нейтральным элементом группоида G2,
так как
e2a2
=
(e1*a1) =
(a1) = a2
и
a2e2
= a2
(доказывается аналогично).
Симметричным для элемента a2 = (a1) группоида G2
является элемент
(a 1')
- образ элемента симметричного a1 в группе G1.
Проверка предоставляется читателю.
По ходу доказательства теоремы мы установили еще
один важный факт. При гомоморфизме группы G1
на группу G2 нейтральный элемент группы G1
отображается в нейтральный элемент группы G2,
а взаимно симметричные элементы из G1
отображаются во взаимно симметричные элементы
из G2.
Выше были рассмотрены группы подстановок.
Важность этих групп определяется тем, что их
подгруппами в известном смысле исчерпываются
все конечные группы. Именно справедливо
следующее предложение, открытое английским
математиком Кэли.
Теорема Кэли. Любая конечная группа G порядка
n изоморфна некоторой подгруппе группы
подстановок.
Доказательство теоремы Кэли несложно и его можно
найти в любой книге по теории групп.
Пусть даны множество произвольных элементов M и некоторая группа его преобразований G. Условимся называть множество M пространством, элементы его - точками, а каждую совокупность точек - фигурой. Фигуру A назовем равной (или эквивалентной), фигуре B, если в группе G существует преобразование, переводящее фигуру A в фигуру B.
Из условий, характеризующих группу преобразований, тотчас следует, что:
1) если фигура A равна фигуре B, то фигура B равна фигуре B (симметричность отношения равенства фигур).
В самом деле, если фигура A равна фигуре B, то некоторое преобразование g группы G преобразует A в B; тогда обратное преобразование g-1 преобразует B в A. Так как по определению группы преобразование g-1 входит в группу G, то в группе G есть преобразование, переводящее B в A, следовательно, фигура B равна фигуре A.
2) если фигура A равна фигуре B и фигура B равна фигуре C, то фигура A равна фигуре C (транзитивность отношения равенства фигур).
Действительно, если A равна B, то в
группе G существует преобразование g, переводящее
A в B; и если B равна C, то в группе G существует
преобразование h, превращающее B в C. Так как
композиция элементов группы также принадлежит
группе, то в G имеется преобразование hg, переводящее фигуру A в
фигуру C. Следовательно, фигура A равна фигуре C.
3) каждая фигура A равна сама себе (рефлексивность отношения равенства фигур).
Это следует из того, что тождественное преобразование принадлежит любой группе преобразований.
Следуя Ф. Клейну, назовем геометрическими такие свойства фигур пространства M и такие связанные с фигурами величины, которые инвариантны относительно любого преобразования из данной группы G и которые, следовательно, одинаковы у всех эквивалентных фигур. Систему предложений о свойствах фигур и величин, инвариантных относительно всех преобразований группы G, мы будем называть геометрией группы G.
Идея Клейна рассматривать различные геометрии как теории инвариантов соответствующих групп, позволила раскрыть глубокие связи между геометриями, открытыми и исследованными к восьмидесятым годам XIX столетия. Эта идея была изложена Клейном в лекции, которую он прочел при вступлении на должность профессора Эрлангенского университета в 1872 году. В этой лекции Клейн призывал переосмыслить все отдельные "геометрии" на основе групповой точки зрения. С тех пор эту точку зрения математики называют "Эрлангенской программой".
Ниже мы собираемся рассмотреть группы симметрий различных плоских фигур. Для понимания этого материала необходимо вспомнить некоторые определения и факты из курса элементарной геометрии, касающиеся геометрических преобразований плоскости.
Подобием называется такое
преобразование на множестве точек плоскости,
которое изменяет расстояния между произвольными
точками плоскости в постоянное число раз k (k>0),
то есть, какие бы две точки M и N мы не взяли, в
результате преобразования подобия они перейдут
в такие точки M' и N', что
M'N' = kMN,
где через MN обозначено расстояние между точками M и N.
В преобразовании подобия точки,
лежащие на одной прямой, преобразуются в точки,
также лежащие на одной прямой с сохранением
порядка их следования. Действительно,
соотношение AB + BC = AC выполняется только для трех
точек одной прямой, таких что B лежит между A и C. Но
из справедливости этого соотношения для точек A,
B, C следует, что A'B' + B'C' = k AB
+ k
BC = k
(AB + BC) = k
AC =
A'C', то есть точки A', B', C' также лежат на одной
прямой и B' - находится между A' и C'.
Таким образом, подобия переводят прямые в прямые. При этом углы между прямыми сохраняются.
Так как композиция подобий является подобием и преобразование обратное подобию также является подобием, то множество всех подобий плоскости образует подгруппу группы всех преобразований плоскости.
Различают подобия первого и второго рода в зависимости от того, имеют ли данная и преобразованная фигуры одинаковые или противоположные ориентации.
Каждое подобие однозначно определяется заданием образов A', B', C' трех точек A, B, C, не принадлежащих одной прямой. На рисунке 16 упомянутые тройки точек задают подобие второго рода.
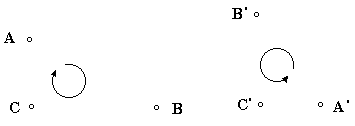
Рис. 16. Преобразование подобия
второго рода
Если известен род подобия, то для его задания достаточно задать образы двух различных точек.
Подобия плоскости с коэффициентом k = 1 образуют важный класс преобразований, сохраняющих расстояния между произвольными точками плоскости. Элементы этого класса называются движениями (или перемещениями) плоскости.
Множество всех движений плоскости образует подгруппу группы подобий этой плоскости.
Также как и подобия, движения делятся на движения первого рода и второго рода. Простейшим движением второго рода является осевая симметрия.
Осевой симметрией (или отражением) относительно прямой l называется движение плоскости, в котором неподвижными являются те и только те точки, которые лежат на прямой l. Прямая l называется осью симметрии. При этом оказывается, что для любой точки M, не лежащей на прямой l, ее образом является такая точка M', что отрезок MM' перпендикулярен прямой l и делится ею пополам.
Осевая симметрия однозначно определяется осью симметрии или парой соответственных точек A и A' (A - A').
Параллельным переносом называется движение плоскости такое, что для любых двух пар соответственных точек A и A', B и B' вектор AA' равен вектору BB'. Другими словами, для любой точки A вектор AA' равен одному и тому же вектору a - вектору переноса.
Параллельный перенос определяется парой соответственных точек A, A' или вектором AA'.
Множество всех параллельных переносов плоскости образует подгруппу группы движений плоскости.
Любой параллельный перенос может быть представлен в виде композиции двух отражений от параллельных прямых.
Центральной симметрией (отражением от точки) называется движение, при котором середины отрезков, соединяющих пары соответственных точек A и A' совпадают с некоторой фиксированной точкой O - центром симметрии.
Центральная симметрия однозначно определяется центром симметрии или парой соответственных точек.
Композиция двух симметрий является переносом (в частности, тождественным преобразованием).
Вращением (или поворотом) на
угол a вокруг точки O называется движение, при
котором точка O остается на месте и каждой точке A
отличной от O ставится в соответствие точка A'
такая, что угол MOM' равен углу .
Вращение является движением первого
рода. Множество всех вращений вокруг
фиксированной точки O образует подгруппу группы
движений плоскости. Композиция двух вращений с
произвольными центрами является либо вращением,
либо параллельным переносом. Отражение от точки
является частным случаем поворота (поворотом с
углом ). Каждое вращение
можно представить в виде композиции двух
отражений от прямых, проходящих через центр
поворота.
Скользящим отражением называется композиция отражения от прямой s и параллельного переноса на вектор параллельный прямой s.
Последовательность выполнения движений, упомянутых в определении скользящего отражения, безразлична.
Любое скользящее отражение может быть представлено в виде композиции трех отражений от прямых.
Теорема о классификации движений плоскости.
Всякое движение плоскости представляет собой одно из трех: а) перенос; б) вращение; в) скользящее отражение, в частности, одно отражение относительно прямой.
Доказательство теоремы можно найти в книге [1, с. 296-310].
Это значит, что любые две равные фигуры на плоскости могут быть переведены одна в другую одним из указанных преобразований. Или еще: каким бы движениям мы не подвергли фигуру, как бы ее ни переносили, ни поворачивали, ни отражали от прямых, результатом будет одно из указанных движений.
Из теоремы о классификации движений плоскости, в частности, следует:
а) всякое движение первого рода является либо параллельным переносом, либо вращением;
б) всякое движение второго рода является либо отражением от прямой, либо скользящим отражением;
в) любое движение может быть представлено в виде композиции не более чем трех отражений от прямых.
Для того, чтобы произвести классификацию всех преобразований подобия, рассмотрим один частный случай подобия - гомотетию.
Гомотетией с центром O и
коэффициентом k отличным от 0 называется такое
подобие плоскости, которое каждой точке M
сопоставляет точку M' такую, что выполняется
равенство: OM'= k OM. Если k
> 0, то точки M и M' лежат по одну сторону от центра
O, при k < 0 - по разные стороны от O.
При k = -1 гомотетия совпадает с центральной симметрией, при k = 1 - с тождественным преобразованием. Соответственные прямые в гомотетии либо параллельны, либо совпадают.
Множество всевозможных гомотетий относительно фиксирован-ного центра O образует подгруппу группы подобий плоскости.
Теорема о классификации подобий плоскости.
Любое преобразование подобия можно представить в виде композиции движения и гомотетии.
На этом мы завершаем обзор преобразований плоскости и переходим к рассмотрению групп симметрий различных плоских фигур.
Симметрия является той идеей, посредством которой
человек на протяжении веков пытался постичь и
создать порядок, красоту и совершенство.
Герман Вейль
Понятие группы позволяет в точных терминах охарактеризовать симметричность той или иной геометрической фигуры. Каждой фигуре F можно сопоставить множество DF всех преобразований плоскости, оставляющих фигуру F инвариантной. Множество преобразований DF образует группу относительно композиции преобразований. Она и характеризует симметричность фигуры. Чем больше преобразований содержится в этой группе, тем более симметричной является фигура F. Так, например, круг более симметричен по сравнению с квадратом.
Если группа DF всех преобразований, оставляющих фигуру F инвариантной, содержит более одного элемента, то она называется группой симметрий фигуры F, а ее элементы - симметриями фигуры F. Если же группа DF состоит из одного тождественного преобразования, то говорят, что фигура F не имеет симметрий. Ниже при изучении симметрий фигур мы ограничимся движениями плоскости.
Если при отражении от точки O фигура F переходит сама в себя, то точка O называется центром симметрии фигуры F. При этом говорят также, что фигура F обладает центральной симметрией.
Например, центром симметрии отрезка является его середина, центром симметрии прямой является каждая точка этой прямой, центром симметрии окружности является ее центр.
Если при отражении от прямой p фигура F переходит сама в себя, то прямая p называется осью симметрии фигуры F. При этом говорят также, что фигура F обладает осевой симметрией.
Например, каждая прямая, проходящая через центр окружности, является ее осью симметрии, осью симметрии равнобедренного треугольника является его высота.
Точку O называют центром поворотной
симметрии порядка n (n - натуральное число, n > 1)
фигуры F, если фигура F остается инвариантной при
повороте вокруг точки O на угол 2/n, и не существует натурального
числа m (m>n) такого, что при повороте вокруг точки
O на угол 2
/m фигура
остается инвариантной. При этом говорят, что
фигура F обладает поворотной симметрией порядка
n.
Например, правильный пятиугольник не
обладает центральной симметрией, но обладает
поворотной симметрией порядка 5, так как при
повороте вокруг точки O на угол 2/5 он отобразится на себя и угол 2
/5 - наименьший из углов,
обладающих таким свойством.
В принципе возможны пять симметрий плоской фигуры: 1) пара-ллельный перенос; 2) центральная симметрия; 3) поворот на угол
0 и
;
4) скользящая симметрия; 5) осевая симметрия.
Но для ограниченной фигуры
параллельный перенос и скользящая симметрия не
являются ее симметриями. В частности, для
многоугольников возможны только три вида
симметрий фигуры: 1) по-ворот на угол (
0,
); 2) центральная симметрия; 3) осевая
симметрия.
Отсюда следует, что всякая симметрия ограниченной фигуры имеет хотя бы одну инвариантную точку.
Наибольший теоретический и прикладной
интерес представляет группа симметрий
правильного n-угольника, называемая диэдричес-кой
группой Dn или группой диэдра. Элементами Dn
являются, во-первых, n поворотов вокруг центра
многоугольника на углы k
= k
(2
/n), где k = 0,1, ..., (n-1), во-вторых, n осевых
симметрий. Осями симметрии служат: в случае
четного n - n/2 диагоналей, соединяющих
противоположные вершины, и (n/2) прямых,
соединяющих середины противоположных сторон; в
случае нечетного n - n высот многоугольника (рис.
17). Других симметрий у многоугольника нет.
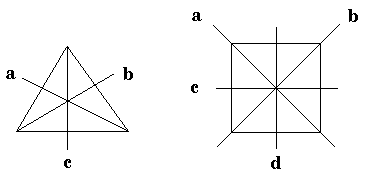
Рис. 17. Оси симметрий
правильных многоугольников
Используя группы симметрий Е. С. Федоров в 1890 году решил задачу классификации правильных пространственных систем точек, являющуюся одной из основных задач кристаллографии. Существует всего 17 плоских федоровских групп, они были найдены непосредственно; пространственных федоровских групп - 230, и только теория групп позволила провести их исчерпывающую классификацию. Это был исторически первый случай применения теории групп непосредственно в естествознании.
Симметрия обозначает тот вид согласованности
отдельных частей, который объединяет их в единое целое.
Красота тесно связана с симметрией.
Г. Вейль. Симметрия
У неограниченных фигур могут быть
элементы симметрии, связанные с переносами.
Такими фигурами, например, являются точки на
прямой, расположенные на равных расстояниях одна
от другой, или квадратная решетка на плоскости
(рис. 18).
Рис. 18. Две фигуры, имеющие в
качестве симметрий параллельные переносы
Фигура, имеющая в качестве симметрии
скользящее отражение, изображена на рисунке 19.
Рис. 19. Фигура, имеющая в
качестве симметрии скользящее отражение
Особый интерес представляют правильные системы фигур на плоскости такие, в которых каждая фигура может быть совмещена с любой другой с помощью некоторого движения, совмещающего всю систему саму с собой. Особое значение правильных систем состоит в том, что они служат геометрическими моделями расположения атомов в кристаллах.
На плоскости примером правильной
системы может служить "паркет" - система
равных многоугольников, покрывающих всю
плоскость, прилегая друг к другу по сторонам.
Паркеты из правильных многоугольников
составляются только из треугольников, квадратов
и шестиугольников (рис. 20) (доказывается,
например, с помощью подсчета углов).
Рис. 20. Паркеты из правильных
многоугольников
Помимо кристаллов симметрия в природе
наблюдается у живых организмов. Подавляющее
число животных, по крайней мере со стороны
внешнего строения, имеет вертикальную плоскость
симметрии; поворотную симметрию имеют морские
звезды (рис. 20). У растений наблюдается симметрия
цветов и симметрия листьев (рис. 21).

Рис. 20. Морская звезда
Рис. 21. Растение
Отражение в воде дает еще один пример
симметрии (рис. 22).
Рис. 22. Отражение в воде
В архитектуре симметрия зданий и
фасадов играет существенную роль, как
геометрическая основа прекрасного (рис. 23).

Рис. 23. Симметричное здание
Решетка сада на рисунке 24 обладает
переносной симметрией.
Рис. 24. Решетка сада
В культурах всех народов мира большую роль играют символы. На рисунках 25-28 приведены изображения некоторых древнейших символов, каждый из которых, как минимум, обладает осевой симметрией.

Рис. 25. Китайский символ Рис. 26. Зонт- азиатский символ Инь-Янь господства
Рис.27.Земной круг индейцев хопи Аризоны
Рис. 28. Символ троицы как эл мент
украшения церковных окон
Читатель легко приведет десятки других
примеров симметрии. Мы же закончим этот раздел
интересным орнаментом (рис. 29), известным под
названием "Куры Пенроуза".
Рис. 29. Куры Пенроуза
Ниже приводится список книг, по которым можно подробнее познакомиться с затронутыми в статье понятиями.
Литература
1. Александров А. Д., Нецветаев Н. Ю. Геометрия. Учебное пособие. - М.: Наука, 1990.
2. Александров П. С. Введение в теорию групп. -М.: Наука, 1980.
3. Дужин С. В. От орнаментов до дифференциальных уравнений: Популярное введение в теорию групп преобразований. - Минск: Вышейшая школа, 1988.
4. Калужнин Л. В., Сущанский В. И. Преобразования и перестановки. - М.: Наука, 1985.
5. Курош А. Г. Теория групп. - М.: Наука, 1967.
Кафедра вычислительной техники
Смоленский государственный педагогический институт им. К. Маркса
Поступила в редакцию 1.06.96.