УДК 611.13/.16+611.423]:616-006-092.9

ПРИНЦИП СИММЕТРИИ КЮРИ И КОНФИГУРАЦИИ МИКРОСОСУДИСТЫХ УЗЛОВ, ИХ СИММЕТРИЯ И АСИММЕТРИЯ, КЛАССИФИКАЦИЯ, ЭНАНТИОМОРФИЗМ МИКРОСОСУДИСТЫХ СЕТЕЙ

© 1996 г. В. А. Глотов

При помощи принципа симметрии Кюри установлена группа симметрии конфигураций микрососудистых узлов и дано объяснение феномена их асимметрии. Предлагается классификация конфигураций микрососудистых узлов по виду отношения "больше-меньше-равно" между параметрами узлов. Установлено 52 класса конфигураций и внутри них 26 зеркально-симметричных пар. Предлагается гипотеза о существовании энантиоморфизма микрососудистых сетей.

В данной работе автор предпринимает попытку при помощи принципа симметрии Кюри и элементов теории симметрии реконст-руировать некотрые закономерности ангиогенеза, отличающиеся влиянием движения крови на развитие конфигурации примитивного микрососудистого узла, возникающего при акте неоангиогенеза, при-водящие к оптималной конфигурации последнего.

Пьер Кюри (1894) сформулировал принцип симметрии так: "При наложении нескольких явлений различной природы в одной и той же системе их диссимметрии складываются. Элементами симметрии системы остаются только те, которые являются общими для каждого явления, взятого отдельно.

Когда некоторые действия проявляют некоторую диссимметрию, то эта диссимметрия должна обнаруживаться и в причинах, их порож-дающих.

Положение, обратное этим двум, несправедливо, по крайней мере практически, т.е. произведенные действия могут быть более симмет- ричными, чем причины"[1].

Формулировку этого принципа для гетерогенных систем в виде:

,(1)

где G_i - группа симметрии i-го явления, взаимодействующего в системе, Gсист. - группа симметрии системы; А. В. Шубников и В. А. Копцик предложили назвать принципом Неймана-Миннигероде-Кюри [2]. В литературе этот принцип еще называют универсальным принципом симметрии, или принципом суперпозиции, или же просто принципом Кюри [3,4,5].

Принцип симметрии Кюри может быть применен при анализе симметрии и асимметрии конфигураций микрососудистых узлов [6]. Для этого микрососудистый узел будем рассматривать как гетерогенную систему, в которой происходит взаимодействие или "наложение" трех потоков крови или трех "явлений", отграниченых друг от друга, т. е., имеющих "различную природу". При этом не имеет значения распадается один из потоков на два других или два потока сливаются в один. Каждый из потоков крови будет оказывать на микрососудистый узел "некоторые действия" , которые будут являться одними из "причин" , "порождающих" его конфигурацию.

Если предположить, что поток крови, движущийся по микрососуду, лежащему в физически изотропной тканевой среде, не испытывает со стороны сосудистой стенки анизотропного конфигурирующего влияния, то под действием сил давления и поверхностного натяжения крови он будет стремиться к оптимальному сокращению своей боковой поверхности, приобретая конфигурацию, характеризующуюся группой симметрии конуса G_кон. :

  (2)

где, в соответствии с правилами, принятыми для записи формул симметрии [3,4], L - одна ось симметрии бесконечного порядка, P - бесконечное число плоскостей симметрии.

Взаимодействие потока крови и эндотелиальной стенки микрососуда порождает конфигурацию просвета последнего конгруэнтную конфигурации потока.

В узле происходит взаимодействие или "наложение" трех потоков или "трех явлений", имеющих конфигурацию с симметрией (2). В соответствии с формулами (1) и (2) устанавливаем группу симметрии G_биф. конфигурации потока крови в бифуркации:

  (3)

где G₁ , G₂ , G₃ - группы симметрии потоков, P - одна плоскость симметрии.

Из (3) следует, что оси симметрии микрососудов в области узла лежат в одной плоскости P.

Взаимодействие потока крови и эндотелиальной стенки узла порождает конфигурацию просвета последнего конгруэнтную конфигурации потока.

Таким образом, узел можно определить как область соединения трех микрососудов, имеющую конфигурацию с симметрией P.

Так как длина микрососуда в реальных микрососудистых сетях, как правило, во много раз больше диаметра просвета, то не смотря на незначительную разницу последнего на его концах будем допускать, что на достаточно малом участке l_i просвет микрососуда имеет круглую цилиндрическую конфигурацию:

    (4)

На рис.1, где d₁ , d₂ , d₃ - диаметры микрососудов, j₁,j ₂,j ₃ - углы между осями симметрии L₁ , L₂ , L₃ микрососудов, эта область обведена толстой линией.

При анализе конфигураций микрососудистых узлов с приме-нением закона сохранения импульса [7,8] установлено,что оси симметрии микрососудов и их продолжения в области узла лежат в одной плоскости и пересекаются в одной точке,

    (5)

при этом

  (6)

При условии: d₁=d₂=d₃ , j₁=j ₂=j ₃ ; конфигурация узла имеет сим-метрию G'_биф. :

(7)

где L₃ - одна ось симметрии 3-го порядка, 3L₂ - три оси симметрии 2-го порядка, 4P - четыре плоскости симметрии.

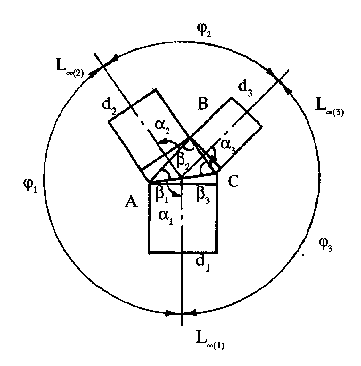
Рис. 1.

При условиях:

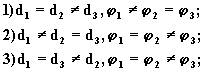
конфигурации узлов имеют симметрию G"_биф.:

    (8)

где L₂ - одна ось симметрии 2-го порядка, 2P - две плоскости симметрии.

Известно, что в реальных микрососудистых сетях практически не встречаются узлы с симметрией конфигураций (7) и (8) [9,10]. Конфигурации микрососудистых узлов всегда асимметричны в плоскости P. Автор предлагает следующее объяснение этого феномена.

В соответствием с принципом симметрии Кюри, при взаимодействии трех потоков крови в узле, последний принимает конфигурацию, группа симметрии (3) которой является наибольшей общей подгруппой групп симметрии конфигураций потоков. Сравнивая конфигурации с симметрией (3), (7) и (8), устанавливаем:

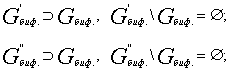
Следовательно, симметрия конфигураций (7) и (8) выше возможной в данном случае, поэтому она не может реализоваться в реальных узлах практически.

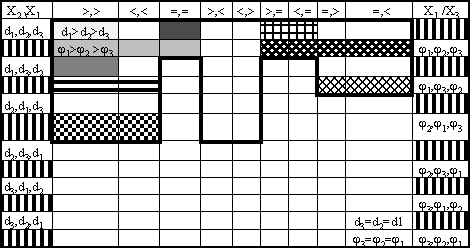
Таблица 1. X₁ x X₂ и X₁ x X₃

Таким образом, принцип симметрии Кюри ограничивает многообразие конфигураций микрососудистых узлов в реальных микрососудистых сетях, "запрещая" существование в них конфигураций с симметрией (7) и (8). По-видимому, процесс конфигурирования микрососудистых узлов имеет стохастический характер, при этом вероятность появления конфигураций с симметрией (7) и (8) - бес-конечно малая величина, а конфигураций с симметрией (3) - величина, бесконечно мало отличающаяся от 1.

Опираясь на универсальные структурные свойства (3)-(6), автор предлагает классификацию конфигураций микрососудистых узлов по виду отношения "больше-меньше-равно" между параметрами d₁, d₂, d₃ и j₁,j ₂,j ₃.

В табл.1 приведено 54 теоретически возможные комбинации элементов множества E {>, <, =} между элеметами множества D{d₁, d₂ , d₃} и F{j₁,j ₂,j ₃ }, где X₁ x X₂ и X₁ x X₃ - декартовы произведения множеств соответственно X₁, X₂ и X₁, X₃ [11], X₁ - множество размещений с повторениями элементов множества E по 2, X₂ и X₃ - множества перестановок соответственно из элементов множества D и F без повторений.

Среди элементов множества X₁ x X₂ и X₁ x X₃ находим все подмножества тождественных и эквивалентных соотношений [12]. Для анализа оставляем по одному их элементу, которые выбираем произвольно, остальные исключаем из дальнейшего рассмотрения. В табл.1 клетки, в которых расположены оставшиеся элементы, обведены общей толстой линией. Плоскость симметрии P конфигурации микрососудистого узла образует с плоскостью поля зрения наблюдателя угол , для которого в общем случае справедливо нестрогое неравенство:

Введем правила индексации параметров d_i и j_i :

1. Если плоскость P образует с плоскостью поля зрения угол  

узел поворачивают на величину угла таким образом, чтобы плоскость P стала параллельной плоскости поля зрения.

2. Если все три микрососуда в узле имеют разные диаметры, то параметру d_i большего микрососуда присваивают индекс i=1, параметрам di следующих по ходу часовой стрелки микрососудов присваивают соответственно индексы i=2 и i=3 (рис. 1).

3. Если все три микрососуда в узле имеют равные диаметры, то параметру d_i случайно выбранного микрососуда присваивают индекс i=1, параметрам d_i следующих по ходу часовой стрелки микрососудов присваивают соответственно индексы i=2 и i=3.

4. Если два из трех микрососудов в узле имеют равные диаметры, то параметру d_i третьего микрососуда присваивают индекс i=1, параметрам d_i следующих по ходу часовой стрелки микрососудов присваивают соответственно индексы i=2 и i=3.

5.Параметру угла j_i между осями микрососудов с параметрами d₁ и d₂ присваивают индекс i=1, параметрам следующих по ходу часовой стрелки углов присваивают соответственно индексы i=2 и i=3 (рис.1).

6. Если плоскость P образует с плоскостью поля зрения угол , то такой узел исключается из рассмотрения, так как ее невозможно индексировать однозначно.

После индексации параметров d_i и j_i среди оставшихся элементов множества X₁ x X₂ и X₁ x X₃ находим все подмножества тождественных и эквивалентных соотношений. Для анализа оставляем по одному их элементу, которые выбираем произвольно, остальные исключаем из дальнейшего рассмотрения. В табл.1 клетки, в которых расположены оставшиеся элементы, выделены различными видами штриховок. В результате этих операций остается 5 видов отношений между элементами множества D - множество (X₁ x X₂ )' и 13 видов отношений между элементами множества F - множество (X₁ x X₃ )'.

В табл.2 приведено 65 теоретически возможных классов конфигураций микрососудистых узлов, где (X₁xX₂)'x(X₁xX₃)' - декартово произведение множеств (X₁xX₂)' и (X₁xX₃)'. Так как в природе не могут существовать конфигурации с симметрией (7) и (8), исключаем из дальнейшего рассмотрения все классы, имеющие эту симметрию. Всего таких классов 13. В табл.2 клетки, в которых они расположены, обведены общей толстой линией. Таким образом, конфигурации реальных микрососудистых узлов принадлежат к одному из 52 классов.

Таблица 2. (X₁ x X₂ )' и (X₁ x X₃ )'

Для одного и того же узла, в зависимости от ее ориентации по отношению к плоскости поля зрения, наблюдатель может регистрировать одну из двух конфигураций, относящиеся к двум разным классам. Назовем такие два класса зеркальной парой. Всего существует 26 зеркальных пар. В табл.2 эти пары соединены между собой двусторонними стрелками. Обозначим зеркальную пару соответственно A_j и A'_j , где j=1,2,3,...,26.

Полученный результат инвариантен по отношению к правилам индексации параметров d_i и _i, приводящим к таблице 5х13 теоретически возможных классов.

Известно, что представители шести классов группы позвоночных: бесчелюстные, рыбы, амфибии, рептилии, птицы и млекопитающие имеют билатерально-симметричную конфигурацию тела и его внутренних систем, характеризующуюся группой симметрии G_m. :

(9)

где P - одна плоскость симметрии [3,13].

Если предположить, что конфигурирование микрососудистых узлов происходит в изотропной тканевой среде, характеризующейся группой симметрии шара G_шар. :

(10)

где L - бесконечное число осей симметрии бесконечного порядка, P - бесконечное число плоскостей симметрии, C - центр симметрии [3], то многообразие ориентаций конфигураций по отношению к плоскости поля зрения также должно характеризоваться симметрией (10). При этом

где P(A_j) и P(A'_j) - вероятности того, что конфигурация случайно выбранного узла принадлежит соответственно к A_j и A'_j классам j-й зеркальной пары.

Назовем микрососудистую сеть ориентированной по отношению к наблюдателю, если известно: 1) в каком органе или образовании и в какой половине тела она локализована; 2) каким образом она ориентирована в этом органе или образовании по отношению к их поверхностям, стандартным осям и плоскостям тела; 3) каким образом она ориентирована в микроскопическом препарате по отношению к предметному и покровному стеклам.

При изучении микрососудистых сетей в каждом отдельном случае правила ориентирования могут быть различными, но предварительно они должны быть обязательно оговорены.

В табл.3 приведено 9 теоретически возможных комбинаций отношений вида "больше-меньше-равно" между параметрами P(A_j) и P(A'_j) в одинаково ориентированных микрососудистых сетях из правой (r) и левой (l) половины тела.

В результате "наложения" в онтогенезе в одной и той же системе процесса конфигурирования тела животного и его внутренних систем, конечным результатом которого является конфигурация с симметрией (9), и процесса конфигурирования микрососудистых узлов при ангиогенезе, конечным результатом которого в потенции в изотропной тканевой среде является ориентация конфигураций, имеющая симметрию (10), в соответствии с принципом симметрии Кюри (1), устанавливаем группу симметрии системы такого "наложения":

где P - одна плоскость симметрии, наибольшая общая подгруппа двух рассматриваемых групп симметрии.

Из табл.3 исключаем все асимметричные по отношению к плоскости P комбинации и комбинации с симметрией (10). В табл.3 клетки, в которых находятся оставшиеся комбинации, обводим общей толстой линией. Таким образом, в реальных микрососудистых сетях правой и левой половины тела возможны только два вида комбинаций отношений между параметрами P(A_j) и P(A'_j).

Таблица 3

Принцип симметрии Кюри ограничивает многообразие ориентаций конфигураций микрососудистых узлов в микрососудистых сетях правой и левой половины тела.

Структурное свойство микрососудистых сетей, являющееся следствием этого ограничения, не тождественное своему зеркальному отражению и которое не может с ним быть совмещено путем перед-вижений и вращения, автор предлагает назвать энантиоморфизмом микрососудистых сетей.

Термин "энантиоморфизм" применяется в кристаллографии для обозначения свойства некоторых веществ кристаллизоваться в "левой" и "правой" модификациях [3,4]. Известно, что энантиоморфные конфигурации могут иметь лишь те объекты, у которых присутствуют только простые оси симметрии и полностью исключены любые инверсионные оси, в том числе плоскости и центр симметрии [3]. Произвольный фрагмент микрососудистой сети имеет L₂ - бесконечное число простых осей симметрии 1-го порядка, т. е. он может быть самосовмещен только после поворота вокруг любой из них на 2p .

Экспериментальная проверка существования энантиоморфизма микрососудистых сетей позволит глубже понять закономерности регуляции ангиогенеза и становления микроангиоархитектоники в системах тела в онтогенезе.

ЛИТЕРАТУРА

1. Кюри П. Избранные труды. - М.-Л.: Наука, 1966. - С. 95-113.

2. Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. -М.: Наука, 1972. - С. 277-285.

3. Шафрановский И. И. Симметрия в природе. - Л.: Недра, 1968.- С. 17-38, 51-63, 84, 100, 104, 153.

4. Шаскольская М. П. Кристаллография. - М.: Высшая школа, 1984. - С. 51-53, 64, 181-182.

5. Белоусов Л. В. Введение в общую эмбриологию. - М.: МГУ, 1980. - С. 187-190.

6. Глотов В. А. Применение универсального принципа симметрии П. Кюри к анализу формы внутреннего просвета сосудов микро-циркуляторного русла и области их разветвлений. //Ишемическая болезнь сердца. - Смоленск: СГМИ, 1993. - С.98-101.

7.Глотов В. А. Правила Ру и конфигурации микрососудистых бифуркаций. //Биофизика, 1992. - Т. 37. - №2. - С. 341-343. [Glotov V.A. The Roux rules and the configurations of microvascular bifurcations. // Bio-physics, 1992. Vol. 37. No.2. Pp. 265-268. Printed in Great Britain].

8. Глотов В. А. Способ определения кинематической вязкости крови в сосудах микроциркуляторного модуля. Патент №1767424. Патентообладатель автор. // Изобретения. - 1992. - №37. - С. 163.

9. Голубь А. С. Асимметричность артериальных микрососудистых разветвлений. //Физиологический журнал СССР им. И. М. Сеченова, 1978. - Т. 64. - №10. - С.1493-1497.

10. Шошенко К. А., Голубь А. С., Брод В. И. и др. //Архитектоника кровеносного русла. - Новосибирск: Наука, 1982. - С. 26-31.

11. Виленкин Н. Я. Индукция. Комбинаторика. - М.: Просвещение, 1976. - С. 24-30.

12. Блох А. Ш., Трухан Т. Л. Неравенства. - Минск: Народная асвета, 1972.

13.Стюарт Я. Концепции современной математики. - Минск: Вышэйшая школа, 1980. - С. 122-144.

Исследование выполнено при поддержке Российского фонда фундаментальных исследований

(проекты РФФИ № 94-04-13544 и №96-04-50991).

Кафедра анатомии человека

Смоленской государственной медицинской академии

Поступила в редакцию 1.03.96.