УДК 611.13/.16+611.423]:616-006-092.9
На практике часто приходится встречаться с ситуациями, когда необходимо вычислить те или иные параметры заданных геометрических объектов или их конфигураций. В ряде случаев бывает удобно произвести преобразование плоскости или пространства, при которых форма рассматриваемых объектов упрощается, произвести необходимые вычисления для образов этих объектов, а затем используя свойства преобразования, получить нужные результаты для оригинала.
Для указанных целей наиболее подходят аффинные преобразования и их разновидности.
Прежде, чем дать определение аффинного преобразования, рассмотрим более общий объект: геометрическое отображение.
Одним из основных понятий современной математики является понятие функции. Переменная y называется функцией переменной x (этот факт записывается следующим образом: y=f(x), если каждому значению x, взятому из какого-то прямые. Пересекающиеся прямые переходят в пересекающиеся допустимого множества значений (область определения функции) отвечает единственное значение y.
Отметим, что в определении функции вовсе не требуется, чтобы x и y представляли собой действительные числа. Напротив, в современной математике принимают, что x и y могут быть элементами произвольной (возможно различной!) природы: точками плоскости и пространства, какими-либо геометрическими фигурами, прямыми или произвольными линиями.
В геометрии особо важную роль играют функции y=Ф(x), где как x, так и y являются точками плоскости или пространства. В таком случае слово “функция” заменяют термином “геометрическое (точечное) отображение. Таким образом, геометрическое отображение представляет собой не что иное, как определённый вид функциональной зависимости y=f(x), где как “аргумент” x, так и “значение функции” y являются точками.
Итак, для задания геометрического (точечного) отображения Ф надо указать:1) некоторую фигуру (точечное множество) А, называемую областью определения отображения Ф; 2) некоторую фигуру А', называемую областью значений отображения Ф и 3) некоторое правило, сопоставляющее с каждой точкой М области А определённую точку M'=Ф(М) области A'.
Если данное отображение Ф переводит точку М в точку M' (т.е. M'=Ф(М)), то точку M' называют образом точки М при отображении Ф. Пусть теперь L - некоторая линия или фигура, целиком расположенная в области А. Если точка М пробегает линию (или фигуру) L, то образ M'=Ф(М) этой точки также пробегает некоторое множество точек L', расположенное в области A'. Это множество L' называется образом множества L при отображении Ф, что записывается следующим образом: L'=Ф(L).
Отображение Ф с областью определения А и областью значений A' называется взаимно однозначным, если, во-первых, ни для каких двух различных точек M и N области А их образы Ф(M) и Ф(N) не совпадают, и, во-вторых, каждая точка области A' является образом некоторой точки при отображении Ф.
Иначе говоря, взаимно однозначное отображение Ф можно охарактеризовать тем, что никакие две различные точки не “склеиваются” в результате отображения Ф и, кроме того, Ф отображает область А не на часть области A', а на всю эту область.
Наибольшую роль в геометрии играют такие взаимно-однозначные отображения, для которых область определения А совпадает с областью значений. Такие отображения называют преобразованиями множества А. Само множество А называется при этом областью действия преобразования Ф.
Таким образом, преобразованием множества А (или, иначе, преобразование с областью действия А) называется всякое взаимно однозначное отображение Ф, для которого область определения и область значений совпадает с А.
Мы ограничимся здесь рассмотрением преобразований, областью действий которых является плоскость, или пространство.
Преобразование плоскости называется аффинным, если при этом преобразовании всякие три точки, расположенные на одной прямой, переходят в три точки, также расположенные на одной прямой.
Укажем основные свойства.
Свойство 1. При аффинном преобразовании всякие три точки, не лежащие на одной прямой, переходят в три точки, также не лежащие на одной прямой.
Свойство 2. Преобразование, обратное к аффинному, является аффинным.
Свойство 3. При аффинном преобразовании плоскости образом всякой прямой является прямая.
Свойство 4. При аффинном преобразовании параллельные прямые переходят в параллельные прямые. при этом точка пересечения прямых переходит в точку пересечения образов этих прямых.
Свойство 5. При аффинном преобразовании внутренние точки треугольника переходят во внутренние точки образа этого треугольника.
Свойство 6. При аффинном преобразовании точка с, делящая отрезок AB в отношении переходит в точку c', делящую отрезок A'B', соединяющий образы A' и B' точек A и B, в том же отношении .
Свойство 7. Пусть A, B, C - три произвольные точки плоскости, не лежащие на одной прямой, а A',B',C' - три другие произвольные точки, также не лежащие на одной прямой. Тогда существует и притом только одно аффинное преобразование плоскости, которое точки A, B, C переводит соответственно в точки A', B', C'.
Введём на плоскости прямоугольную систему координат xOy с началом в точке О.
Рассмотрим аффинное преобразование на этой плоскости. Пусть М - точка с координатами (x,y), а M' - образ этой точки с координатами (x',y').
Свойство 8. Координаты (x,y) точки М и
координаты (x',y') образа этой точки M' при аффинном
преобразовании связаны соотношением:
где
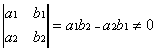
Если при рассматриваемом преобразовании образом треугольника ABC является треугольник A'B'C', то отношение площадей этих треугольников равно
Аффинное преобразование пространства определяется так же, как и аффинное преобразование плоскости.
Для аффинных преобразований пространства выполняются следующие свойства.
При аффинном преобразовании пространства прямая переходит в прямую.
При аффинном преобразовании пространства плоскость отображается на плоскость и это отображение является аффинным преобразованием.
При аффинных преобразованиях пространства сохраняется параллельность прямых и плоскостей.
При аффинных преобразованиях пространства сохраняется порядок точек на прямой и отношение отрезков. лежащих на одной прямой или двух параллельных прямых.
Существует и притом только одно
аффинное преобразование пространства,
которое четыре данные точки A, B, C, D, не лежащие
в одной плоскости переводит в произвольно
заданные четыре точки A', B', C', D' , также не лежащие
в одной плоскости [1-3].
1
Начиная с классических работ W. Roux [4], в поле зрения исследователей, изучающих сердечно-сосудистую систему, появился новый объект - сосудистый узел, морфологическое образование, возникающее в месте разделения или соединения сосудов, отличающееся от сосудистой трубки в морфологическом и функциональном плане.
Конфигурация микрососудистого узла характеризуется сле-дующими параметрами: диаметрами просветов микрососудов, образующих узел, углами между осями этих микрососудов; которые в свою очередь зависят от гемодинамических параметров (динамическая вязкость и плотность крови, скорость потока крови и др.) [4].
Просвет микрососудистого узла имеет плоскость симметрии P. Оси симметрии микрососудов лежат в плоскости симметрии P и пересекаются в одной точке внутри треугольника ABC (рис. 1),
Рис. 1.
где di (i=1,2,3) - диаметры микрососудов, ji - углы между осями симметрии L (i) этих микрососудов, ai - углы между осями симетрии этих микрососудов и соответствующими сторонами треугольника ABC , которые есть большие оси эллипсов, образующихся при сечениях микрососудистого узла тремя плоскостями, перпендикулярными плоскости симметрии и проходящими через стороны треугольника ABC. Эти сечения есть границы перехода внутрених просветов микрососудов во внутренний просвет микрососудистого узла. Малые оси эллипсов есть диаметры соответствующих микрососудов. Три эллиптические сечения соприкасаются в вершинах треугольника ABC [4].
Что представляет из себя форма внутреннего просвета микрососудистого узла?
Единственное геометрическое тело, которое идеально соответствует установленным для формы внутреннего просвета микрососудистого узла геометрическим свойствам, есть фрагмент, отсеченный тремя секущими плоскостями, перпендикулярными плоскости симметрии P и проходящими через стороны треугольника ABC, от вещественного эллипсоида (в дальнейшем просто "эллипсоида"), который имеет следующее каноническое уравнение:
где a, b, c - полуоси эллипсоида. Линии
пересечения эллипсоида с плоскостями
представляют собой эллипсы. Симметрия
эллипсоида имеет следующую формулу:
L23PC ,
где L2 - ось симметрии 2-го порядка,
P - плоскость симметрии, C - центр симметрии. Одна
из плоскостей симметрии эллипсоида совпадает с
плоскостью симметрии P микрососудистого узла.
Теорема. Около каждого треугольника можно описать бесконечно много эллипсов.
Доказательство. а) Рассмотрим
треугольник (рис. 2), вершины которого A'B'C'
находятся в точках с координатами (-1,0), (0,1), (1,0).
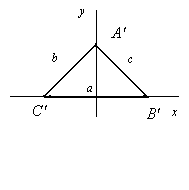
Рис. 2.
Эллипс, описанный около этого
треугольника, будем искать в виде
Точка (0,C) - центр эллипса. Соотношения
между параметрами эллипса найдем подставляя
вместо (x, y) в уравнение эллипса координаты точек
B' и C'
.
Отсюда находим:
.
Параметр c определяем из условия
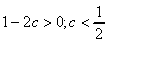
Таким образом, каждый из эллипсов
семейства
описан около рассмотренного треугольника.
Пусть теперь ABC - произвольный треугольник. Рассмотрим аффинное преобразование, отображающее A'B'C' в ABC. Это преобразование отобразит семейство эллипсов, описанных около A'B'C' в семейство эллипсов, описанных около ABC.
Пусть d1'/2, d2'/2, d3'/2 - полуоси эллипсов перпендикулярных плоскости симметрии искомого эллипсоида. Построим в этой плос-кости треугольник со сторонами d1',d2',d3' (рис.3).
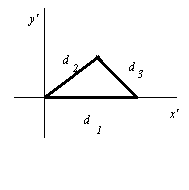
Рис. 3.
Опишем около этого треугольника
окружность, а затем построим сферу с центром в
центре построенной окружности и радиусом, равным
радиусу окружности. Через стороны треугольника
проведем сечения, перпендикулярные плоскости
треугольника. Получим 3 круга. Рассмотрим
аффинное преобразование пространства в себя, при
котором аппликата точки не меняется, а
построенный треугольник переходит в данный. При
этом круговые сечения перейдут в заданные
эллипсы, а рассматриваемая сфера перейдет в
искомый эллипсоид.
Лемма. Форме внутреннего просвета микрососудистого узла, имеющей параметры di, ji, ai может соответствовать только фрагмент единственного эллипсоида, имеющего полуоси a, b, c [4].
Доказательство. Уравнение
поверхности второго порядка имеет вид:
Так как плоскость Z=0 является плоскостью симметрии поверх-ности, то коэффициенты при z обращаются в 0. Следовательно a13=0, a23=0, a3=0.
Остается 7 параметров. Разделив на параметр, отличный от нуля, получаем 6 параметров. Отсюда следует, что поскольку исходные данные содержат 9 параметров и рассматриваемая поверхность существует, то она единственна.
Либо иными словами: Уравнение
эллипсоида, плоскостью симметрии которого
является плоскость xOy, зависит от 9 параметров. В
условии задачи задается 9 параметров.
Следовательно эллипсоид один, т. е. определяется
единственным образом.
2
Аффинным преобразованием плоскости в
себя называется преоб-разование, задаваемое
соотношениями
где
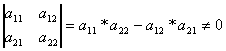
При этом преобразовании точка M c координатами (x,y) переходит в точку M' с координатами (x',y').
Если выполнены соотношения
,
то начало координат при таком преобразовании остается непод-вижным. В дальнейшем будем рассматривать только такие преоб-разования.
Матрица
называется матрицей аффинного
преобразования. Если задано преобразование
то точка с координатами (1,0) перейдет в точку с координатами (a11, a21), а точка с координатами (0,1) перейдет в точку с координатами (а12, а22).
Отметим следующие свойства аффинных преобразований, которые потребуются нам в дальнейшем:
Свойство 1. При аффинном преобразовании параллельные прямые переходят в параллельные прямые.
Свойство 2. При аффинном преобразовании сохраняется отношение отрезков, лежащих на одной прямой или на параллельных прямых.
Свойство 3. Существует одно и только одно аффинное преоб-разование плоскости, переводящее данные три точки, не лежащие на одной прямой в три другие заданные точки, также не лежащие на одной прямой.
Свойство 4. При аффинном преобразовании эллипс переходит в эллипс.
системы координат выберем в вершине A, ось x направим вдоль стороны с длиной a, ось y в сторону вершины b. Найдем координаты Пусть дан треугольник со сторонами а, b, c (рис. 3). Начало прямоугольной вершин этого треугольника.
Вершина A имеет координаты (0,0), c - (a,0). Для нахождения координат вершины B найдем сначала cos(A). Воспользуемся с этой целью соотношением
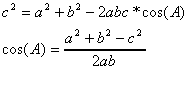
Находим теперь sin (A):
.
Теперь мы можем найти координаты
вершины B. Они соответственно равны
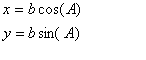
Пусть дан треугольник со сторонами a, b, c. Предположим, что система координат на плоскости выбрана, как описано в п. 2. Найдем координаты центра описанной окружности для рассматриваемого треугольника.
Уравнение перпендикуляра,
проведенного к середине стороны AC имеет вид
.
Найдем уравнение перпендикуляра,
проведенного к середине сто-роны AB. Координаты
середины стороны AB равны
.
Угловой коэффициент стороны AB равен tg(A). Угловой коэффициент перпендикуляра к AB будет равен - ctg (A).
Уравнение перпендикуляра имеет вид
.
В результате получим
.
Пусть имеются два треугольника с общей вершиной O в начале координат. Координаты остальных двух вершин первого треугольника обозначим через (x1, y1), (x2, x2), а второго треугольника через (x1', y1'), (x2', y2). Найдем аффинное преобразование, переводящее первый треугольник во второй.
Аффинное преобразование с матрицей
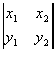
переводит точку с координатами (1, 0) в точку (x1, y1), а точку с координатами (0, 1) в точку (x2, y2).
Аффинное преобразование с матрицей
переводит точку с координатами (1, 0) в точку (x1', y1'), а точку с координатами (0, 1) в точку (x2', y2').
Тогда аффинное преобразование с
матрицей
переведет точку (x1,y1) в точку (x1',y1'), а точку (x2, y2) в точку (x2',y2').
Пусть в плоскости XOY задан треугольник со сторонами a, b, c, одна из вершин которого совпадает с началом координат. Имеются три эллипса, плоскости которых, перпендикулярны плоскости XOY, стороны данного треугольника являются осями этих эллипсов. Оси эллипсов, перпендикулярные плоскости XOY, равны соответственно d1', d2', d3'. Требуется найти эллипсоид для которого эти эллипсы будут сечениями.
Строим треугольник со сторонами d1', d2', d3' в плоскости XOY таким образом, что одна из вершин этого треугольника, принад-лежащая стороне с длиной d1', совпадает с началом координат, ось OX направлена по этой стороне, третья вершина лежит в той же полуплоскости, что и положительная полуось OY.
Строим сферу, центр которой находится в центре описанной окружности этого треугольника, радиус равен радиусу этой окружности.
Строим сечения этой сферы плоскостями, проходящими через стороны рассматриваемого треугольника и перпендикулярные плоскости XOY. Эти сечения представляют собой окружности, диаметры которых соответственно равны d1', d2', d3'.
Рассмотри теперь аффинное
преобразование пространства, за-данное
следующим образом
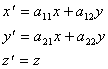
где
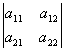
матрица аффинного преобразования, переводящего рассматриваемый треугольник со сторонами d1', d2', d3' в заданный треугольник со сторонами a, b, c. При этом построении сфера перейдет в требуемый эллипсоид.
Найдем уравнение этого эллипсоида. По
формуле Герона площадь треугольника со
сторонами d1', d2', d3' равна
.
Радиус описанной окружности равен
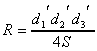
Координаты центра описанной
окружности для рассматриваемого треугольника
равны
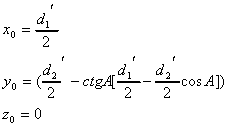
где
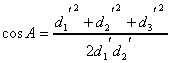
.
Уравнение сферы
.
Уравнение эллипсоида
.
Матрица
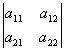
¦
обратна матрице
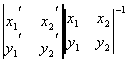
где
,
,
,
,
,
,
,
,
,
,
,
.
Преобразуя уравнение эллипсоида
получим
.
Введем в рассмотрение матрицу C,
определяемую соотношением
,
где - матрица,
транспонированная к матрице A. Тогда уравнение эллипсоида
имеет вид
Рассмотрим сечение этого эллипсоида плоскостью XOY и найдем параметры полученного эллипса.
Углы, образуемые этими осями с осями
координат, определятся из соотношения
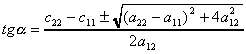
Полуоси:
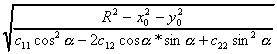
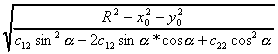
Центр эллипсоида находится в точке с
координатами
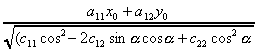
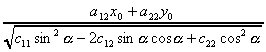
Введем обозначения
Положим
,
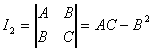
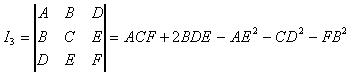
Тогда полуоси рассматриваемого
эллипсоида будут соответственно равны
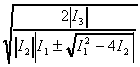
Угол, образуемый одной из этих осей с
осью OX, определяется из соотношения
,
где - корень уравнения
.
Координаты центра эллипсоида
удовлетворяют системе уравнений
т. е. ¦
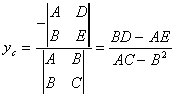
Построение
характеристического треугольника по параметрам
микрососудистого узла
Найдем стороны треугольника АВС (рис. 1) по параметрам микрососудистого узла.
1). Уравнение прямой на плоскости,
проходящей через точку с координатами (x0,y0)
имеет вид
.
Это уравнение можно переписать в виде
, (1)
где
.
Вектор n(a,b) перпендикулярен данной прямой.
2). Уравнения прямых, параллельных
прямой (1) и отстоящих от нее на расстояния d/2
имеют вид
,
.
3). Прямая, проходящая через начало координат задается уравнением
.
4). Пусть вектор n(a,b) образует с осью 0y
острый угол (b>0), прямая задана уравнением
.
Прямая, которая получается из данной
прямой поворотом на угол против часовой стрелки
относительно начала координат имеет уравнение
. (2)
5). Две прямых, заданных уравнениями
и не параллельных между собой,
пересекаются в точке с координатами
(3)
.
6). Рассмотрим прямую, проходящую через
начало координат
,
(b>0).
Проведем пару прямых, параллельных
данной и отстоящих от нее на расстоянии d1/2:
, (4)
. (5)
Повернем эту прямую на угол1
против часовой стрелки. Получим прямую
,
где a2, b2 определяются
соотношением (2). Проводим пару прямых, отстоящих
от этой прямой на расстоянии d2/2
, (6)
. (7)
Повернем теперь исходную прямую на угол j=j1 + j2 против часовой стрелки относительно начала координат.
Получим прямую
,
где 3, b3
определяются из соотношения (2).
Проводим пару прямых, параллельных
этой прямой и отстоящих от нее на расстоянии d3/2:
, (8)
. (9)
Пользуясь формулами (3) находим
координаты точек пересечения прямых (4,7), (6,9), (8,5).
Обозначим эти точки через A, B, C . После этого
находим длины сторон треугольника ABC.
3
ПРОГРАММА ДЛЯ ВЫЧИСЛЕНИЯ ОБЪЕМА И ПЛОЩАДИ ПОВЕРХНОСТИ ФРАГМЕНТА ЭЛЛИПСОИДА , ОБРАЗУЮЩЕГОСЯ В ОБЛАСТИ СТЫКА МИКРОСОСУДОВ В МИКРОСОСУДИСТОМ УЗЛЕ
НА АЛГОРИТМИЧЕСКОМ ЯЗЫКЕ
СВЕРХВЫСОКОГО УРОВНЯ MATHCAD 3.0
The parameters of bifurcation
d1:=35
d2:=16
d3:=28
The computation of the coordinates of the characteristic triangle
The normal vectors to the bifurcation axis
n1:=cos[]+isin[]
n2:=n1(cos(-f1)+isin(-f1))
n3:=n2(cos(-f2)+isin(-f2))
The conclusion of the equations of straight lines, parallel to the
bifurcation axis.
a1:=Re(n1) b1:=Im(n1)
a2:=Re(n1) b2:=Im(n2)
a3:=Re(n3) b3:=Im(n3)
a1*x+b1*y=d1/2
a1*x+b1*y=-d1/2
a2*x+b2*y=d2/2
a2*x+b2*y=-d2/2
a3*x+b3*y=d3/2
a3*x+b3*y=-d3/2
The coordinates of the summits of characteristic triangle (x1,y1), (x2,y2), (x3,y3) in the plane x', y', let us consider the help triangle with the summits in the points (120*tg(pi/6),-30), (0,90), (120*tg(pi/6),-30)
The affin mapping maps the summits of the characteristic triangle in the summits of the help triangle let us write so:x'=a*x+b*y+c, y'=d*x+e*y+f. Let us compute the parameters
of the mapping.
Let us compute the parameters of the reverse mapping.
In the space x'y'z' let us consider the sphere x'^2+y'^2+z'^2=8100. The
searched ellipsoid has the equation (a'x+b*y+c)^2+(d*x+e*y+f)^2+z^2=8100. Let us compute
its parameters.
A:=a2+d2
B:=ab+de
C:=b2+e2
D:=ac+df
E:=bc+ef
F:=c2+f2-8100
The center of the ellipsoid is situated at the point
xc:=c1
yc:=d1
xc:=0
Let us compute the halfaxis of ellipsoid p1,p2,p3
I1:=A+C
I2:=AC-B2
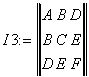
p3:=90
The angle between one of the axis and 0x is determined so:
The volume of the ellipsoid upon the characteristic triangle
v:=4.666104
ЛИТЕРАТУРА
1. Яглом И. М., Атанасян Л. С. Геометрические преобразования. Энциклопедия элементарной математики. Книга 4. - М.: Государ-твенное издательство физико-математической литературы, 1963.
2. Яглом И. М., Ашкинузе В. Г. Идеи и методы аффинной и проективной геометрии. Часть 1. - М.: Учпедгиз, 1962.
3. Моденов П. С., Пархоменко А. С. Геометрические преобразования. - М.: Издательство МГУ, 1961.
4. Глотов В. А. Структурный анализ микрососудистых бифуркаций. (Микрососудистый узел и гемодинамический фактор). - Смоленск: АО "Амипресс", 1995.
5. Воднев В. Т., Наумович А. Ф., Наумович Н.
Ф. Основные математические формулы. - Минск:
Вышейшая школа, 1988.
Исследование выполнено при поддержке Российского фонда фундаментальных исследований
(проекты РФФИ №94-04-13544 и
№96-04-50991).
Кафедра алгебры и геометрии
Кафедра вычислительной техники
Смоленский государственный педагогический институт им К. Маркса
Кафедра анатомии человека
Смоленская государственная медицинская академия
Поступила в редакцию 1.05.96.