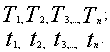
УДК 51

МЕТОДИКА РАСЧЕТА И ПРОГРАММНОЕ ОБЕСПЕЧЕИЕ ДЛЯ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ ПРИ АППРОКСИМАЦИИ НЕЛИНЕЙНЫХ ХАРАКТЕРИСТИК ЭКСПОНЕНЦИАЛЬМИ ПОЛИНОМАМИ

© 1996 г.   Л.  Л.  Лямец

В статье изложена математическая методика аппроксимации экспериментальных графиков экспоненциальными полиномами. Предлагаемый способ математической обработки позволяет рассматривать реакцию исследуемой системы как сумму экспоненциальных процессов и может эффективно применяться для анализа свойств систем и объектов, подчиняющихся законам пропорционального роста.

Для аналитического исследования свойств систем, содержащих нелинейные элементы, необходимо экспериментальные кривые, характеризующие нелинейную зависимость между входным воздействием и реакцией, представить в виде непрерывных аналитических функций в заданном интервале значений аргумента.

Как правило, точное представление экспериментальной кривой в виде некоторой аналитической зависимости невозможно, да и в этом практически нет необходимости, так как сама экспериментальная кривая, подлежащая аппроксимированию, содержит неточности, вызванные погрешностью измерительной аппаратуры, и, кроме того, различные экземпляры нелинейных элементов одного и того же типа имеют заметный разброс по характеристикам. Поэтому необходимо осуществлять аппроксимирование экспериментальных кривых с помощью непрерывных аналитических функций, которые давали бы приближение к экспериментальной кривой с погрешностью, не превышающей заданную.

В работе [3] описан способ аппроксимации экспериментальных кривых экспоненциальными полиномами и изложена методика расчета коэффициентов аппроксимации интерполяционным методом. Особен-ностью интерполяционного метода приближения является то, что количество экспоненциальных составляющих вдвое меньше числа экспериментальных точек. Если число экспериментальных точек значительно, то применение этого метода приводит к полиному очень высокого порядка, практически бесполезному.

Одним из методов, позволяющих повысить качество аппроксимации, является метод наименьших квадратов (или регрессия). При этом методе число отсчетов экспериментальных значений функции и ее аргумента может быть намного больше степени аппроксимирующего экспоненциального полинома. При реализации данного метода объединяются статистическая обработка данных и полиномиальная аппроксимация. Полученный экспоненциальный полином дает наилучшее приближение, при котором среднеквадратическая погрешность по всем точкам минимальна. При этом кривая аппроксимирующей функции проходит через облако точек исходной зависимости, а требование о равенстве ее значений ординатам узловых точек снимается.

Основные положения методики вычисления коэффициентов аппроксимации экспоненциального полинома по методу наименьших квадратов изложены в работе [1]. Пусть заданы соответственные значения функции T и независимого переменного t

Необходимо аппроксимировать данную, экспериментально установленную зависимость, полиномом вида

(1)

Полином (1) содержит m членов, причем 2m<n. На основании имеющихся экспериментальных данных можно составить систему уравнений

(2)

где h - значение шага независимой переменной t.

Введем обозначения

После подстановки принятых обозначений в выражение (2) получим

(3)

Для решения системы (3) предположим, что z₁, z₂, z₃, ..., zm являются корнями некоторого полинома вида

(4)

Умножим первое из уравнений системы (3) на S_m, второе уравнение на S_(m-1) , m-е уравнение на S_(m-(m-1)) и сложим первые (m+1) уравнений. Выполняя данную процедуру, начиная со второго, затем с третьего и последующих уравнений, применяя к полученным выражениям метод приведения, получим систему из (n-m) уравнений

(4)

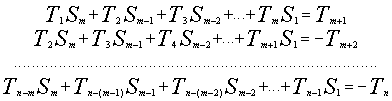
Решение системы (5) относительно S₁, S₂,..., S_m с использованием метода наименьших квадратов, описанного в [1], позволяет получить систему нормальных уравнений

(5)

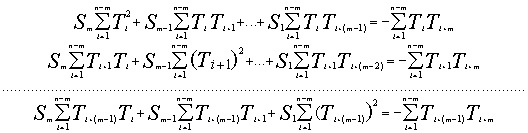
Коэффициенты перед величинами S_i вычисляются по имеющимся значениям функции T_i , измеренным в дискретные моменты времени t_i. Решение данной системы определит значения S₁, S₂,..., S_m. Задачи на решение систем линейных уравнений относятся к задачам линейной алгебры. Эти задачи настолько распространены и важны, что для их реализации предложены многие десятки алгоритмов. Один из самых простых - алгоритм Гаусса. Для проведения вычислений может быть использована программа на языке Паскаль, описанная в работе [2] .

Последующие расчеты связаны с вычислением корней полинома (4). Программа на языке Паскаль, описанная в работе [2], полностью автоматизирует процесс нахождения всех m корней полинома с действительными коэффициентами. Алгоритм программы реализует метод Хичкока. В его основе лежит итерационный процесс выделения из полинома квадратичного множителя, корни которого (как корни квадратного уравнения) легко вычисляются аналитически. Затем полином делится на этот множитель, что понижает на 2 его порядок, и этот процесс повторяется до нахождения оставшихся корней. При этом использование аппарата комплексной арифметики позволяет найти комплексные корни.

Вычисление корней полинома (4) даст значения z₁, z₂, ..., z_m. Любой корень z_m записывается в виде

Определенность значений z₁, z₂, ... , z_m позволит рассчитать значения a₁, a₂, ..., a_m из выражения

по формуле

Для действительных положительных корней _m 0. Для определения коэффициентов E_i можно использовать алгоритм вычисления коэффициентов регрессии общего вида, при которой экспериментальные точки графических зависимостей приближаются выражением

(7)

где f_i(t) - экспоненциальные функции вида

с известными коэффициентами a_i. Для вычисления коэффициентов регрессии надо решить систему линейных уравнений

(8)

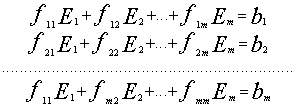
где

причем j = 1, 2, ..., m и k = 1, 2, ..., m.

Этот метод реализует программа, описанная в работе [2]. Перед ее использованием необходимо задать константу N (число функций) и уточнить процедуру F_i, вписав в нее экспоненциальные функции с известными коэффициентами a_i.

Качество аппроксимации экспериментальных данных выражением (1) можно оценить сравнением средней квадратичной относительной погрешности аппроксимации с относительной погрешностью метода измерения. Средняя квадратичная погрешность аппроксимации Ф определяется по формуле:

(9)

где T_iаппр - численные значения функции согласно аппроксимации; T_iэксп - экспериментальные значения; n - количество экспериментальных точек. Предполагается, что точность аппрок-симации экспериментальных результатов достаточна, если средняя квадратичная погрешность аппроксимации не превышает по величине значение относительной погрешности измерения в эксперименте.

Применение данной математической методики позволяет опре-делить численные значения коэффициентов аппроксимации и опти-мальное количество экспоненциальных составляющих в полиноме (1). Коэффициенты аппроксимации E_i и a_i можно рассматривать как параметры, характеризующие передаточную функцию нелинейной системы и определяющие всю экспериментальную кривую.

При анализе нелинейных систем аппроксимирующий полином определяет структуру уравнений, подлежащих решению. В случае электрических схем под аргументом t понимают сумму гармонических составляющих. Аппроксимирование полиномом (1) представляет значительный интерес, так как в общем случае показательная функция может быть разложена в ряд Лорана с коэффициентами разложения, представляющими функции Бесселя. В результате все промежуточные выкладки для получения искомых уравнений, подлежащих решению, опускаются и получается система уравнений, решение которой не представляет принципиальных затруднений.

Литература

1. Безикович Я. С. Приближенные вычисления. - М.: Гостехиздат, 1949. - 463 С.

2. Дьяконов В. П., Круглов В. В. Научно-технические расчеты на Турбо-Паскале. Справочное пособие. - М.: Наука, 1993. - 242 C.

3. Лямец Л. Л., Аппроксимация нелинейных характеристик экспо-ненциальными полиномами. // Вторая военно-научная конференция ВА ПВО СВ РФ. Ч. 2. - Смоленск: СВА ПВО СВ РФ, 1995. - С. 146 - 150.

Смоленская Военная академия ПВО СВ РФ.

Поступила в редакцию 1.04.96.