УДК 577.3+611.13/.16
Адвентиция стенки кровеносного
сосуда может быть представлена в виде
каркаса из эластино-коллагеновых элементов,
заполненного рыхлой соединительной тканью. В
статье рассматривается модель вязко-упругого
эластино-коллагенового элемента, представляющая
собой видоиэмененную сдвоенную модель Максвелла
с введением элемента, учитывающего особенности
поведения коллагеновых волокон при растяжении.
Приведены закономерности деформаций
вязко-упругого элемента и расчетных напряжений в
нем в зависимости от скорости приложения
нагрузки.
При изучении строения стенки кровеносных сосудов вполне определенно установлено, что их наружная оболочка (adventia) в рыхлом слое соединительной ткани содержит большое количество косых и продольных толстых эластитновых и коллагеновых волокон, которые и обусловливают необходимую жесткость стенки сосуда для неизменности формы просвета сосуда при его деформации (изгибе) [1,2,3]. Эластиновые и коллагеновые волокна в совокупности образуют в адвентиции своеобразный жесткий (по сравнению с окружением) каркас, расположение и количество отдельных элементов которого вариабельно в зависимости от многих факторов: вида сосуда, его локализации, возраста, патологии и пр. Каждый такой эластиново-коллагеновый элемент обладает вполне определенными механическими свойствами. Для описания закономерности напряженно-деформированного состояния эластиново-коллагенового элемента при приложении к нему нагрузки в данной работе предлагается к рассмотрению его механическая модель.
Результаты механических испытаний кровеносных сосудов показывают, что их материал является вязко-упругим и обладает всеми свойствами, характерными для таких тел - последействием и релаксацией напряжений [1]. Эти данные о характере деформации стенки сосуда как единого целого справедливы и для наружного слоя в частности, поскольку упругие эластиновые и коллагеновые волокна находятся в вязкой среде соединительной ткани.
В механике для описания деформационных процессов таких тел применяются модели Максвелла, Фойгта, Кельвина и более сложные их сочетания [4, 5]. Предлагаемая автором модель вязко-упругого эластино-коллагенового элемента (рис. 1) представляет собой видоизмененную сдвоенную модель Максвелла с введенеим дополнительного элемента, учитывающего особенности поведения коллагеновых волокон при их растяжении. Упругие свойства эластина здесь представлены элементом Е1, а коллагена - элементами Е0 и Е2. Вязкие свойства композитного материала адвентиции обусловлены наличием в ней рыхлой соединительной ткани и воды "связанной" полимерами, а также "свободной" воды и представлены в модели элементом .
При приложении к
эластино-коллагеновому элементу в начально
расслабленном состоянии растягивающего усилия Q
его - деформация (удлинение) определяется
жесткостью E1F1 волокон эластина,
поскольку в это время происходит выпрямление
спиральности полипептидных цепей молекул
коллагена без включения в работу
непосредственно коллагеновых фибрил. Это
свойство коллагеновых волокон отмечено, в
частности, в [6] и на предлагаемой модели
представлено элементом Е0. Поскольку Е0<<Е1,
то практически, до достижения удлинения
вязко-упругого элемента 
вся нагрузка воспринимается волокнами эластина.
На следующей стадии процесса растяжения стенки
сосуда (l > a) растягивающая нагрузка Q
воспринимается совместно волокнами эластина
(элемент Е1 ) и коллагена (элемент Е2).
Модули упругости эластина и коллагена
отличаются в конечное число раз Е2 > Е1
и Е2=kE1. По данным разных авторов
значение k колеблется от 10 до 333 [2,4,6].
Относительная деформация (удлинение)
cтенки сосуда в
некоторый момент времени будет определяться
напряжениями
s
1 иs 2, возникающими в эластиновых и коллагеновых волокнах при их совместной работе (рис. 2).
В свою очередь напряжения растяжения s1 и s 2 определяются из выражений
где F1 и F2 - площади
поперечных сечений эластиновых и коллагеновых
волокон в вязкоупругом элементе, а q1 и q2
- усилия, приложенные к эластиновым и
коллагеновым волокнам.
Таким образом
или
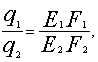
т. е. распределение элементарных растягивающих усилий, приложенных к эластиновым и коллагеновым волокнам пропорционально их жесткостям (E1F1 и E2F2).
Вязкоупругое тело, соединяющее свойства упругого тела и вязкой жидкости, характерно тем, что на величину его деформации и возникающих при этом напряжений существенное влияние оказывает скорость деформации de/dt. При линейно напряженном состоянии s=lde/dt , где l=3h- линейная вязкость жидкости, а h- коэффициент вязкости жидкости [7].
В целом линейную деформацию вязко-упругого тела
можно представить как сумму деформаций упругого и вязкого элементов e0=eу +e в . eу =s/e, где Е - некий обобщенный модуль упругости эластино-коллагенового элемента, определяемый соотношением содержания в нем волокон эластина и коллагена, а - расчетное значение напряжений в эластино-коллагеновом элементе при этом Е. Учитывая, что скорость изменения деформации вязкого элемента
общая скорость изменения деформации
эластино-коллагенового элемента будет
Введя в рассмотрение коэффициент n =l/E имеем
При достижении вязко-упругим элементом
в некоторый момент времени t0 постоянной
деформации e=e0
напряжение в нем
т.е. убывают с течением времени, наблюдается явление релаксации. Постоянная n имеет размерность времени и является временем релаксации.
При описании быстропротекающих процессов в кровеносных со-суах в рассмотрение необходимо вводить мгновенный (динамический) модуль упругости В для рассматриваемого материала [4,7]. Всегда В> Е.
Уравнение, описывающее изменение
деформаций и напряжений в вязко-упругом элементе
с учетом скорости изменения деформаций
приведены в [7].
,
по которому деформации и напряжения
будут определяться выраже-ниями:
На рисунке 3 показана зависимость
напряжений в вязко-упругом элементе от его
деформации (удлинения). Прямые s1=E1e и s1=B1e отображают
случаи упругой деформации отдельно эластинового
во-локна в элементе при скоростях деформации de/dt ®0 и 
, а прямые s=Ee и s=Be- такие
же процессы для совместной работы эластиновых и
коллагеновых волокон. В реальности, при конечных
скоростях деформаций de/dt
процесс должен отображаться экспоненциальными
кривой 1 для эластинового волокна и кривой 2 для
эластино-коллагенового элемента. При деформации
эластино-коллагенового элемента из начально
расслабленного состояния по достижениии
значения ea=a/l происходит
включение в работу коллагеновых волокон, что на
рисунке 3 соответствует участку перехода 3 на
кривой s=f(e),
а в экспериментальных наблюдениях
сопровождается резким ростом модуля упругости
испытываемой стенки сосуда [1].
При функционировании стенки сосуда деформация эластиново-коллагеновых элементов ее адвентиции при стабильной нагрузке зависит от ее (нагрузки) динамичности.
При de/dt= 0 , т.е. при стабилизации нагрузки, деформация будет
экспоненциально возрастать по кривой 1
(рис.4) до значения e= s0/e , что отображает процесс ползучести
эластино-коллагенового элемента. Если в
некоторый момент времени нагрузка снимается, то
начальная деформация вязко-упругого элемента
будет также убывать по экспоненциальному закону
до нуля (кривая 2, рис.4), т.е. наблюдается явление
последействия.
Выводы
1. При расчетах напряжений и деформаций в наружной оболочке кровеносного сосуда ее возможно рассматривать как каркас из отдельных эластино-коллагеновых вязко-упругих элементов, основные механические характеристики которых обусловлены соотношением содержания (площадей сечений) эластиновых и коллагеновых волокон в адвентиции, а также степенью гидратации рыхлой соединительной ткани.
2. Определенные закономерности деформирования эластино-коллагенового элемента позволяют включить его в математические модели функционирования кровеносного сосуда с учетом различных скоростей (динамики) приложения внешних нагрузок к адвентиции.
Рис.1. Модель вязко-упругого
эластино-колагенового элемента
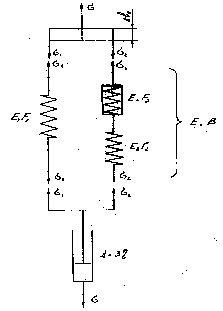
Рис.2. Распределение напряжений между
эластиновыми и колаге-новыми волокнами при их
совместной работе.
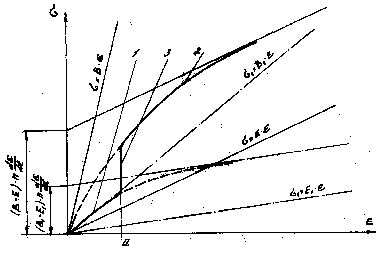
Рис. 3. Изменение напряжений в вязко-упругом элементе в зависимости от его деформации.
1 - изменение напряжений в эластиновых волокнах;
2 - изменение расчетного значения напряжений в вязко-упругом элементе при совместной работе эластинового и коллагенового волокон;
3 - включение в работу коллагеновых волокон, a .
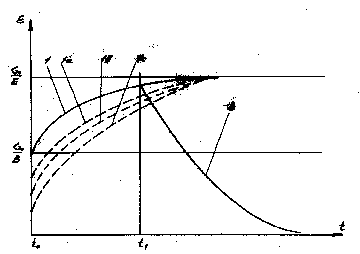
Рис. 4. Зависимость деформации вязко-упругого элемента после ста-билизации нагрузки в момент времеи t0.
1 - рост деформации при стабильной нагрузке. 1a, 1b, 1c - нарастание деформации после стабилизации нагрузки (ползучесть), приложенной с различными скоростями
.
2 - уменьшение деформации после снятия
нагрузки в момент времени t1 .
Литература
1. Пуриня Б. Я., Касьянов В. А. Биомеханика крупных кровеносных сосудов человека. - Рига. :"Зинатне", 1980.
2. Никулин А. А., Петров В. К. Кровеносные сосуды.-Тула.:Приокское книжное издательство, 1981.
3. Ванков В. Н. Строение вен. - М.: "Медицина", 1974.
4. Владимиров Ю. А. и др. Биофизика. - М. :"Медицина", 1983.
5. Варданян Г. С. и др. Сопротивление материалов с основами теории упругости и пластичности. - М.: Издательство ассоциации строительных вузов, 1995.
6. Каро К. и др. Механика кровообращения. - М.: "Мир", 1981.
7. Гастев В. А. Краткий курс сопротивления материалов. - М.: "Наука", 1977.
Исследование выполнено при поддержке Российского фонда фундаментальных исследований
(Проекты РФФИ 94-04-50544 и 96-04-50991).
Смоленский областной институт патологии
Кафедра анатомии человека
Смоленская государственная медицинская академия
Поступила в редакцию 1.04.96.