ИССЛЕДОВАНИЕ ПРИЛОЖИМОСТИ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДЛЯ ОПИСАНИЯ ВОЗРАСТНЫХ ИЗМЕНЕНИЙ СТРУКТУРЫ ОРГАНОВ

Доклад на Всесоюзной конференции по возрастной морфологии. (Самарканд, осень 1972 г.)

Придерживаясь этой точки зрения, следует a priori наделить объекты изучения некоторыми свойствами, т.е. попытаться определить эти объекты с наибольшей доступной строгостью, как это обычно делается в математике. Такой подход даст возможность и в морфологической науке строить те же цепи безупречных рассуждений, что и в математике, потому что законы, по которым разрешается делать непротиворечивые выводы, одинаковы независимо от природы объекта, к которому они применяются. К этому имеет отношение только природа нашего разума, а она одинакова и у математика и у морфолога.

Рассмотрим, прежде всего, возрастные изменения сосудистой стенки. Здесь, как в каждой морфологической теории, quot homines, tot sententiae (сколько людей - столько мнений), в полном сответствии с известной латинской поговорке. Строя свою теорию развития возрастных изменений сосудов, L. Jores (1924), оперирует такими морфологическими данными:

1) у эмбриона нет возрастных изменений интимы;

2) возрастные изменения развиваются неравномерно и неодновременно в разных отделах артериальной системы;

3) существуют постепенные переходы от возрастных изменений к патологическим;

4) у животных отсутствуют возрастные утолщения внутренней оболочки.

Н. Н. Аничков (1940) полагает, что доводы L. Jores "не соответствуют фактическому материалу", потому что, опираясь на свой собственный опыт исследования возрастных изменений сосудов, он в каждом случае, когда L. Jores делает отрицательное утверждение, берется сделать положительное.

Мы с самого начала должны принять, что такая различная трактовка одного и того же материала является прямым следствием своеобразия этого материала, а не вызвана тем, что тот или иной исследователь чего-то недосмотрел или что-то преувеличил. Говоря более определенно, следует допустить. что природа возрастных изменений сосудистой стенки достаточно сложна, так что самая естественная альтернативная трактовка ее, как у L. Jores и Н. Н. Аничкова, должна быть изменена. Весь вопрос в том, каким образом это сделать? Основная трудность - отсутствие необходимых и достаточных формальных критериев, на которые можно было бы оперться. Стреллер, например, предлагает учитывать такие особенности старения:

1) эндогенность, т.е. свойство, присущее организму вне зависимости от окружающей среды. Организм должен состариться при самых благоприятных внешних условиях;

2) универсальность, т.е. свойство, характерное для целой группы животных (иначе оно было бы результатом мутации);

3) постепенность развития;

4) разрушительность.

Как видно, все это сугубо качественные характеристики, и их формализация очень трудна, если вообще возможна. Пойдем по иному пути.

На международном конгрессе анатомов, гистологов и эмбриологов, проходившем в Ленинграде в 1970 г, И. Шарф предложил использовать для описания возрастных изменений дифференциальные уравнения. Сам он проанализировал ряд конкретных примеров возрастных изменений в нервной системе и, привлекши самую современную вычислительную технику, получил необходимые уравнения эмпирически. Отвлекаясь несколько в сторону, заметим, что дифференциальные уравнения действительно представляют собой превосходный аппарат для описания морфологических изменений в возрастном аспекте. Имея дифференциальное уравнение и задав некоторые условия, в которых проводились наблюдения, прежде всего исходные значения тех морфологических признаков, изменение которых хочется проследить во времени, мы вправе считать, что будем точно знать значение этого морфологического признака то или иное время спустя, уже не выполняя измерений в соответствующие сроки.

Так теоретически и должно обстоять дело при анализе возрастных изменений и в нервной системе, и в любых других структурах. В самом деле, коль скоро задано дифференциальное уравнение, вместе с ним задано и его фазовое пространство, т.е. множество всех состояний процесса - настоящих, прошедших и будущих. Кривые, которые описывают течение таких различных процессов, как количество нейронов в коре больших полушарий, или число кровоизлияний в головной мозг, или, наконец, потребление мозгом кислорода, весьма сходны между собой, и это убедительно показано И. Шарфом. Можно считать, следовательно, что все эти процессы, несмотря на явное отличие их по природе друг от друга, являются элементами одного и того же фазового пространства.

Продолжая эти рассуждения, естественно допустить, что элементами того же фазового пространства являются возрастные изменения в сосудистой и пищеварительной системах. Но если наделить такое фазовое пространство только теми свойствами, которые оно уже получило благодаря исследованиям И. Шарфа, то оказывается, что нельзя понять многие возрастные изменения сосудов, например, те, о которых сказано выше в связи с работами L. Jores и Н. Н. Аничкова. Требуется дополнительный анализ данных И. Шарфа. Оставляя в стороне собственно математическую сторону дела, ограничимся некоторыми итогами.

Оказалось, что дифференциальное уравнение, описывающее возрастные изменения в нервной системе, имеет решение колебательного характера. Это значит, что изображая, например, количество нервных клеток в коре полушарий в зависимости от возраста, мы получим не монотонно убывающую кривую, как это думал И. Шарф, а волнообразную кривую типа синусоиды. Выходит, что даже если пользоваться только качественными критериями оценки, мы не в праве говорить, например, так: с возрастом количество нейронов в коре уменьшается. Коль скоро взять для исследования такой промежуток времени, как пятое десятилетие жизни, найдутся последующие годы, в которые количество нейронов в коре будет больше, чем в предыдущие, и наоборот.

По аналогии можно заключить, что так же дело обстоит с сосудистой и пищеварительной системой. Эта аналогия имеет достаточно веские основания, потому что периодический характер жизненных процессов - известное явление. Не приходится специально говорить, например, о биологических ритмах, изученных биохимиками и физиологами. Изменения морфологических структур являются следствием таких ритмов, и было бы странным, если бы периодических колебаний количества морфологических структур не существовало.

Таким образом, пытаясь наиболее полно понять, какими должны быть возрастные изменения в органах и тканях, мы прежде всего должны взглянуть на них как на колебательный процесс. Это - первое требование, которое надо предъявить к рассматриваемому нами фазовому пространству; изучаем ли мы возрастные изменения в нервной, сосудистой или пищеварительной системах, - все равно надо уже a priori допустить, что мы получим ту или иную периодическую функцию.

Анализ морфологических изменений в возрастном аспекте может представить интерес лишь в том случае, когда в итоге будет получена не одна отдельная кривая, суммирующая результат данных конкретных наблюдений, а выявлена некая общая закономерность, которую можно будет проследить во всех последующих наблюдениях, произвольно выбирая те или иные условия их проведения. В связи с этим необходимо обсудить некоторые детали, налагающие определенные ограничения на использование в данной ситуации общих методов обработки экспериментальных данных, - те ограничения, что продиктованы колебательным характером возрастных изменений.

Пусть дан набор эмпирически найденных точек – результаты измерений того или иного морфологического признака в разных возрастных группах. По ним надо провести кривую, описывающую изучаемый процесс. Обычно мы делаем следующее допущение. Мы считаем, что несовпадение результатов отдельных наблюдений – следствие случайных ошибок измерений.

При этом допущении становится возможным использовать метод наименьших квадратов, позволяющий найти кривую, наиболее удовлетворительно описывающую результаты измерений.

Иными словами мы допускаем, что результаты измерений в разных случаях данной возрастной группы – это то же самое, как если бы измерения проводились повторно в одном и том же случае.

Все это имеет смысл, когда речь идет о монотонно возрастающих или убывающих функциях (кривых). В нашем же случае ситуация сложнее. Если считать, что изучается колебательный процесс, надо искать кривую также среди волнообразных кривых, так что использование метода наименьших квадратов в его классической, наиболее привычной форме исключается. И далее, при нашем подходе требуется вначале "угадать" характер кривой, к которой ищется приближение. Имея в виду периодический процесс, это почти невозможно сделать. Более того, необходимым условием использования метода наименьших квадратов является требование, чтобы отдельные измерения были выполнены в один и тот же момент времени. Этому требованию никак нельзя удовлетворить, рассматривая общепринятое деление на возрастные группы, например, по десятилетиям.

Учитывая все сказанное, откажемся, по крайней мере, на этот раз, от того взгляда, что различные значения морфологического признака в одной и той же возрастной группе суть следствия случайных ошибок.

Именно, определяя, например, число нервных клеток в коре мозга в двух случаях данной возрастной группы, будем считать, что разница между ними реально существует, а не является следствием случайного процесса, появляясь в результате ошибки измерений. Проводя измерения тщательно, мы уже в силу одного этого гарантированы от того, что случайная ошибка существенным образом исказит результат измерения. Иными словами, само исследование и в особенности проведение измерений планируется таким образом, чтобы сделать случайную ошибку меньше известной постоянной величины.

Тогда можно видеть в различии результатов отдельных измерений то, как ведет себя функция в окрестности данной точки в данный возрастной период. Более подробно такой подход можно описать следующим образом. Пусть мы произвели измерения количества старчески измененных нервных клеток в возрастной группе 40-60 лет у 10 человек и получили соответствующие 10 точек. Мы полагаем тогда, что эти измерения выполнены на одном человеке в разное время на протяжении 20 лет, так что, упорядочивая соответствующим образом результаты измерений во времени, мы получим данные о характере поведения искомой функции.

Задача сводится, следовательно, к тому, чтобы упорядочить результаты измерений. органах.

Пусть требуется определить, в каких отделах происходит более обширный возрастной фиброз - в аорте или коронарных артериях сердца.

Исследуя развитие соединительной ткани в этих сосудах у одного и того же человека в один и тот же срок (по паспортным данным), мы имеем основание производить сравнение лишь в том случае, если уверены, что сравниваем в один и тот же момент, т.е. если нет оснований усомниться в том, что развитие изменений в различных отделах происходят синхронно. Поскольку таких оснований, вообще говоря, нет, необходимо добиться синхронизации с помощью некоторых математических преобразований найденных величин и тогда уже проводить сравнения.

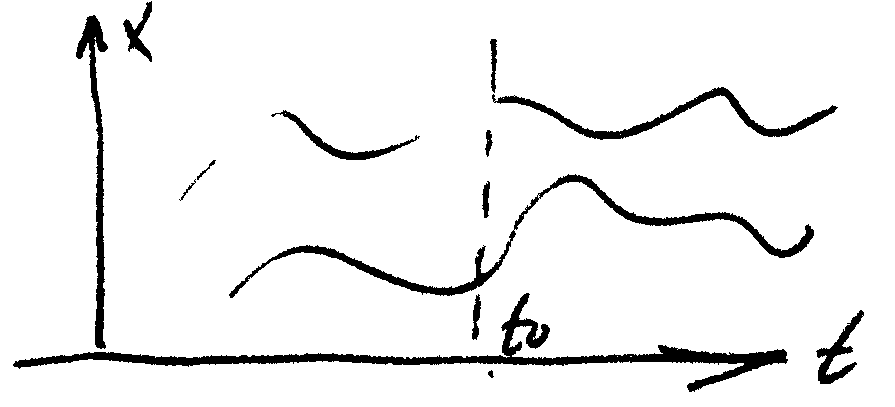
Как же проводить эти преобразования? Надо, вообще говоря, эмпирически найденные функции заменить другими, однозначно им соответствующими, и провести замену всех функций по одному и тому же правилу. После такой замены мы получим вполне однородные по своим свойствам элементы, которые имеют, например, такой вид (Рис. 1).

Рис. 1.

Восстанавливая в любой точке оси абсцисс (resp. временной оси) перпендикуляр, мы чисто формально находим точки его пересечения с кривыми х(t).

Очевидно, теперь сравнение можно проводить с полным основанием, сопоставляя результаты, соответствующие одному и тому же моменту времени.