УДК 519.21: 621.396.969.1

 

СОВМЕСТНЫЕ  ПЛОТНОСТИ  ВЕРОЯТНОСТЕЙ  ОГИБАЮЩИХ
И  ФАЗ  СМЕСИ  ДЕТЕРМИНИРОВАННОГО  ГАРМОНИЧЕСКОГО
СИГНАЛА  И  КВАЗИГАРМОНИЧЕСКОГО  ШУМА
В  СУММАРНОМ  И  РАЗНОСТНОМ  КАНАЛАХ  ПРИЕМНОГО
ТРАКТА  ОБЗОРНОЙ  МОНОИМПУЛЬСНОЙ  РЛС

 

© 2003 г. С.  А. Вашкевич, С. Н. Деркач

 

После выхода статьи [1] в редакцию поступило несколько отзывов с просьбой обосновать предположение о независимости плотностей вероятностей огибающих и фаз смеси детерминированного гармонического сигнала и квазигармонических шумов в суммарном и разностном каналах приемного тракта обзорной моноимпульсной (МИ) РЛС. В большинстве отзывов ставится под сомнение данный факт ввиду того, что полезный сигнал в обоих каналах от одного и того же источника (цели).

 

Цель данной статьи – проверить указанное предположение при условии, что шумы в каналах независимы.

В качестве модели квазигармонических шумов в каналах тракта обработки обзорной МИ РЛС целесообразно использовать модели независимых узкополосных стационарных случайных процессов с симметричной спектральной плотностью, которые, как известно [2], наиболее полно отражают характеристики шумов приемного тракта РЛС.

Данные процессы достаточно полно изучены [2] и в дальнейшем будут использованы только результаты их анализа.

Представим смесь детерминированного гармонического сигнала и квазигармонического шума в каждом из каналов в виде:

 

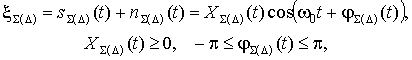    (1)

 

где ;  – амплитуда детерминированного гармонического сигнала;  – промежуточная частота приемного тракта;  – коэффициент, учитывающий ослабление сигнала в разностном канале приемного тракта;  – огибающие смеси сигнала и шума в соответствующем канале;  – результирующие фазы смеси сигнала и шума в каналах;  – шумы в соответствующих каналах тракта обработки.

Воспользовавшись представлением узкополосных процессов в виде квадратурных составляющих, используемым в [2], запишем выражения для  и :

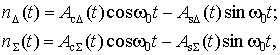      (2)

где ,  – соответствующие квадратурные составляющие шумов в суммарном и разностном каналах.

Тогда квадратурные составляющие для огибающей смеси детерминированного сигнала и шума в каждом из каналов с учетом выражений (1) и (2) (предполагая, что начальная фаза детерминированного сигнала равна 0), можно записать в виде

 

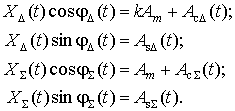     (3)

 

В векторной форме данные выражения поясняются на рис. 1, а и б в прямоугольной системе координат (пунктиром обозначены случайные изменения векторов во времени).

 

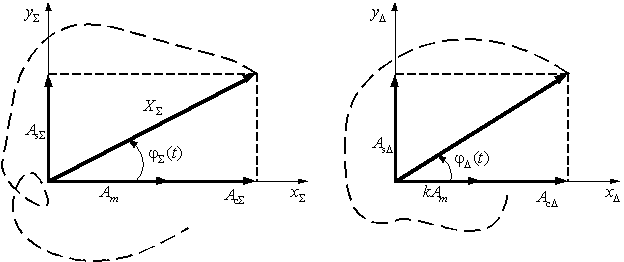
а                                                              б

 

Рис. 1. Геометрическое представление смеси детерминированного

сигнала и квазигармонического шума

 

Перепишем выражения (3) в виде

 

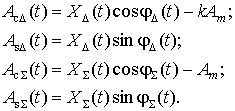      (4)

 

Найдем совместную плотность вероятностей для случайных величин (СВ), стоящих в левых частях выражений (4).

В [2] доказывается, что квадратурные составляющие узкополосного случайного процесса, взятые в один и тот же момент времени, всегда некоррелированные, а для гауссовых процессов и независимы. Их дисперсии равны .

Поэтому, используя выражение для многомерного нормального распределения [3]:

 

,

 

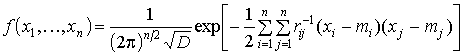где  – определитель ковариационной матрицы;

 – элементы матрицы, обратной по отношению к ковариационной матрице  системы СВ (x1, …, xn);

mi – математические ожидания,

и, рассчитав определитель ковариационной матрицы и элементы обратной ей матрицы:

 

,          ,

 

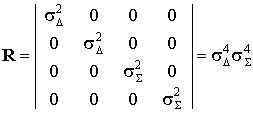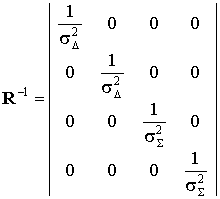запишем совместную плотность для квадратурных составляющих , , ,

 

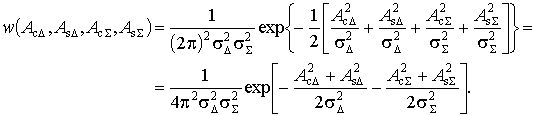     (5)

 

Перейдем от переменных , , ,  к новым переменным  ,  , используя выражения (4).

Нетрудно убедиться, что модуль якобиана преобразования переменных

 

 

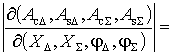
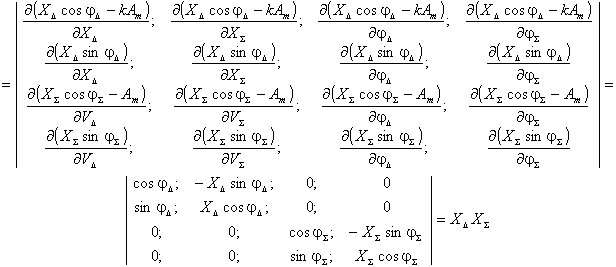
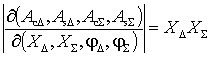.    (6)

 

Подставив выражения (4) в формулу (5), с учетом значения якобиана преобразования (6), получим

 

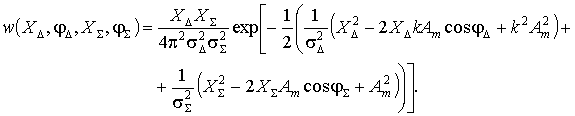 (7)

 

Воспользовавшись свойством согласованности плотностей вероятностей, путем интегрирования по независимым переменным, получим совместные плотности вероятностей для огибающих и фаз в суммарном и разностном каналах приемного тракта обзорной МИ РЛС, взятых в один и тот же момент времени:

 

,

,

 

 

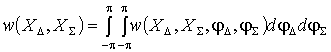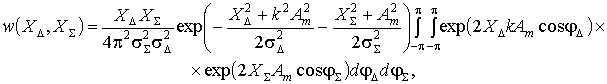
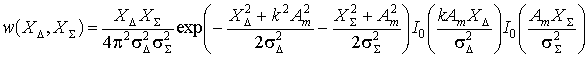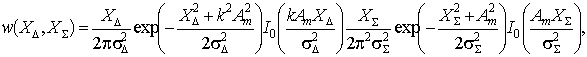
(8)

 

где  – модифицированная функция Бесселя нулевого порядка от мнимого аргумента.

Из выражения (8) очевидно, что совместная плотность вероятностей огибающих в суммарном и разностном каналах представляет собой произведение одномерных плотностей вероятностей огибающих в суммарном и разностном каналах, распределенных по закону Райса. Как известно [3], если возможно представить совместную плотность вероятностей системы СВ в виде произведения одномерных плотностей вероятностей, то данная система состоит из независимых СВ.

Выполнив интегрирование выражения (7) по  и , получим

 

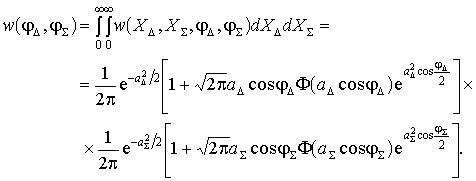  (9)

 

где ,  – отношение сигнал/шум по напряжению в соответствующих каналах обработки;

 – интеграл вероятности.

Из выражения (9), как и из (8), очевидно, что совместная плотность вероятностей для фаз также представляет собой произведение двух одномерных плотностей вероятностей, свидетельствуя о независимости распределения фаз в каналах приемного тракта обзорной МИ РЛС.

Таким образом, проведенные исследования подтверждают предположение о независимости плотностей вероятностей огибающих и фаз смеси детерминированного гармонического сигнала и квазигармонических шумов в суммарном и разностном каналах приемного тракта обзорной МИ РЛС.

Литература

 

1. Вашкевич С. А. Нахождение плотности вероятности оценки углового рассогласования для обзорной амплитудной суммарно-разностной моноимпульсной системы. – Математическая морфология. Электронный математический и медико-биологический журнал. – Т. 5, вып. 1. – 2003. – URL:http://www.smolensk.ru/user/sgma/MMORPH/N-9-html/vashkevich/VASHKE~1.html

2. Статистическая радиотехника: Примеры и задачи / Под ред. В. И. Тихонова. М., Сов. радио, 1980. 544 с.

3. Вентцель Е. С., Овчаров Л. А. Теория вероятностей и ее инженерные приложения. М., Наука, 1988. 480 с.

 

 

JOINT  DENSITIES  of  PROBABILITIES  of  ENVELOPES  And PHASES  of  a  combine  DETERMINED  HARMONIC

SIGNAL  And  ALMOST  HARMONIC  NOISE  In  TOTAL  And INCREMENTAL  CANALS  of  a  RECEIVING  СHANNEL  of  the SURVEY  MONOPULSE  radar  station

 

S. A. Vashkevich, S. N. Derkach

 

After an exit of the article [1] in edition some recalls with the request have acted to justify the conjecture of independence of densities of probabilities of envelopes and phases of a combine of the determined harmonic signal and almost harmonic noises in total and incremental canals of a receiving channels of the survey monopulse radar station. In the majority of the recalls the given fact whereas a desired signal in both canals from the same source is put under doubt.

 

Кафедра радиоэлектроники

Военный университет войсковой ПВО ВС РФ

Поступила в редакцию 5.11.2003.