УДК 681.518.2

Многие задачи, связанные с управлением сложными системами и поддержкой принятия решений, такие как выработка оптимальной стратегии управления, поиск рациональных решений и т.д., могут быть сведены к задачам поиска оптимальных путей в направленных графах, в которых вершинами являются элементы пространства состояний системы (элементы дерева решений). При этом специфика предметной области вносит ряд дополнительных особенностей.

Во-первых, в подавляющем большинстве случаев оценка процессов управления и принятия решений носит многокритериальный характер, причем частные критерии оценки, как правило, взаимозависимы.

Следующей особенностью является наличие неопределенности, обусловленной, с одной стороны, неточностью исходных данных, а с другой тем фактом, что в качестве источника информации выступает человек (лицо, принимающее решения), при этом информация имеет явно выраженный качественный характер.

Основные методы учета неопределенности информации могут быть отнесены к следующим трем категориям: вероятностные, эмпирические и нечеткие.

Использование вероятностного подхода к задачам управления и поддержки принятия решений затрудняется тем, что требования, налагаемые на входные данные и промежуточные величины, часто оказываются невыполнимыми. Вероятностное пространство событий состоит из элементарных событий, считающихся несовместными. Это обусловливает ту особую роль, которую играют в статистической теории независимые случайные величины. В реальной же ситуации исходные данные, а также частные критерии выбора и оценки решений почти всегда взаимозависимы. Часто бывает трудным или невозможным получение выборки достаточного объема для того, чтобы статистические оценки были достоверными. Кроме того, при вероятностном подходе очень сложно описать факт отсутствия информации.

Что касается эмпирических методов, таких как использование “факторов уверенности” [1, 2], или байесовский подход оценки свидетельств [2], и т.п., то не известны теоретически обоснованные границы их применимости.

С другой стороны, теория нечетких множеств, сформулированная Л. Заде [3], позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы, что оказывается особенно полезным, когда рассматриваемые процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. При этом согласно теореме FAT (Fuzzy Approximation Theorem) [4], доказанной Б. Коско, любая математическая система может быть аппроксимирована системой, основанной на нечеткой логике. Следовательно, формализация неопределенности в виде нечеткости обладает целым рядом преимуществ применительно к задачам управления и поддержки принятия решений.

Таким образом, задача поиска оптимальных путей в направленных графах является весьма актуальной в рамках проблематики управления сложными системами и поддержки принятия решений. При этом специфика предметной области обуславливает дополнительные требования, а именно наличие нечеткости (неопределенности) исходной информации и многокритериальный характер оценки процессов управления и принятия решений.

Для дальнейшего изложения целесообразно привести определение базового математического объекта – направленного нечеткого графа. Направленным нечетким графом называется пара множеств, в которой – множество вершин графа; , – нечеткое множество направленных ребер графа, вершина является началом, – концом ребра ; – значение функции принадлежности для ребра [5]. Причем вершины являются инцидентными в том и только в том случае, если . Кроме того, .

Использование данного математического объекта в задачах управления и принятия решений требует решения следующих проблем. Во-первых, необходимо определить множество вершин нечеткого графа. В общем виде данное множество будет соответствовать множеству элементов пространства состояний системы, под которым, в частности, можно понимать множество элементов дерева решений. Во-вторых, для задания направленного нечеткого графа требуется определить значения функций принадлежности ребер графа .

Ребро направленного нечеткого графа в рассматриваем контексте описывает некоторое изменение состояния системы или процесса принятия решения. Данное изменение может быть определено набором частных нечетких показателей , в качестве которых выступают нечеткие множества. Кроме того, так как имеет место многокритериальность, должна быть определена система частных критериев оценки . При этом, естественно, мощность множеств и совпадает.

Последовательность построения функции принадлежности состоит из следующих шагов. Во-первых, формируется нечеткое отношение предпочтения на множестве частных критериев оценки . Во-вторых, формируются нечеткие отношения предпочтения на всех множествах локальных вершин . Под множеством локальных вершин будем понимать множество всех вершин, связанных с k-й исходящими ребрами, то есть множество всех j-х вершин, для которых . В-третьих, формируется нечеткое множество недоминируемых локальных вершин , функция принадлежности которого и будет определять значения функции принадлежности ребер, связывающих k-ю вершину со всеми, принадлежащими множеству . После этого направленный нечеткий граф можно считать построенным.

Формирование нечеткого отношения предпочтения на множестве частных критериев оценки осуществляется следующим образом. Лицо, принимающее решения задает матрицу парных сравнений степеней важности частных критериев . При этом используются оценки, приведенные в таблице 1 [5].

, (1)

где , .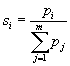

Данный подход к формированию системы предпочтений лица, принимающего решения позволяет учитывать неопределенность индивидуальных предпочтений, а также взаимную зависимость критериев оценки решения. Он может быть эффективно реализован в виде опроса, при этом требуемая информация задается в простой лингвистической форме.

Для формирования нечетких отношений предпочтения на множествах локальных вершин необходима процедура, обеспечивающая оценку степени оптимальности частного нечеткого показателя . В том случае, если частные нечеткие показатели являются нечеткими числами, нормированными таким образом, что их оптимальные значения стремятся к нулю, данная процедура может иметь следующий вид.

Вводится в рассмотрение нечеткое число специального вида – нечеткий ноль с функцией принадлежности

(2)

где h – положительная константа. При этом степень оптимальности частного нечеткого показателя может быть определена как

, (3)

где – множество положительных действительных чисел;

– операция пересечения нечетких множеств.

Тогда функция принадлежности нечеткого отношения предпочтения по частному критерию оценки h^t на множестве локальных вершин будет иметь вид

, (4)

(5)

где 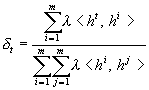– коэффициент важности t-го частного критерия оценки.

Таким образом, сформировав нечеткие отношения предпочтения на всех множествах локальных вершин, можно перейти к построению нечеткого множества недоминируемых локальных вершин. Функция принадлежности данного нечеткого множества определяется выражением

. (6)

Поиск оптимального пути в построенном таким образом направленном нечетком графе может быть осуществлен с помощью алгоритма Дейкстры [6]. При этом аддитивные веса вершин, используемые в данном алгоритме, будут определяться суммированием величин, равных для соответствующих ребер графа.

Литература.

1. Брукинг А., Джонс П., Кокс Ф. и др.; под ред. Форсайта Р. Экспертные системы. Принципы работы и примеры / Пер.с англ. – М.:Радио и связь, 1987. – 224с.
2. Уотермен Д. Руководство по экспертным системам / Пер. с англ. – М.:Мир, 1989. – 388с.
3. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений / Пер. с англ. – М.: Мир, 1976. – 165 с.
4. Круглов В.В., Борисов В.В. Гибридные нейронные сети. – Смоленск: Русич, 2001. – 224 с.
5. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. – М.: Наука. Гл. ред. физ.-мат. лит., 1990. – 272 с.
6. Кристофидес Н. Теория графов. Алгоритмический подход / Пер. с англ. – М.: Мир, 1978. – 432 с.

Golubev Igor V.

   This article describes the approach for realization of optimal routes finding procedure applicable to directed fuzzy graphs. Given approach enables to perform optimal routes finding under multicriterial route costs’ evaluation conditions.

СМПО НИЦ ВА ВПВО ВС РФ

Поступила в редакцию 23.09.2006.