МЕТОДЫ ПРОГНОЗИРОВАНИЯ МНОГОМЕРНЫХ РЯДОВ

УДК 519.6

МОДЕЛИ ПРОГНОЗИРОВАНИЯ
МНОГОМЕРНЫХ СЛУЧАЙНЫХ ПРОЦЕССОВ

Ó2006 г. Петрова Е. В.

Анализируется опыт применения различных видов моделей для прогнозирования многомерных случайных процессов. Выявляются наиболее перспективные модели: модель векторной авторегрессии и нейросетевая модель.

Актуальность задач прогнозирования в современных условиях достаточно высока. Качество их решения может в значительной степени повлиять на принятие того или иного решения в различных сферах деятельности.

Часто для решения задач прогнозирования применяется статистический аппарат корреляционного анализа, который строится на предыдущих значениях одномерного случайного процесса. Это обстоятельство не позволяет устанавливать причинно-следственные связи параметров прогнозируемой системы в целом. Очевидно, для повышения качества прогноза необходимо проводить одновременный анализ сразу нескольких доступных показателей. Следовательно, задача прогнозирования должна быть сведена к прогнозированию многомерного временного ряда, каждый элемент которого будет являться одним из связанных параметров системы.

Было показано [1], что для решения таких задач наиболее перспективными с точки зрения эффективности прогноза являются модели векторной авторегрессии (VAR) и нейронной сети.

Базовая модель VAR основана на статистическом подходе к прогнозированию и является обобщением метода авторегрессии для многомерного случая. В работе [2] имеется математическое описание данной модели.

Пусть имеется m процессов y_it, i = 1,…,m и t = 1,…,N (число временных отсчетов). Тогда в матричной форме модель векторной авторегрессии имеет вид:

. (1)

Базовой предпосылкой для модели (1) являются предположение, что вектор остатков e_t представляет собой вектор белого шума, то есть:

, .

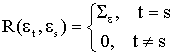Кроме того, матричные коэффициенты должны удовлетворять условиям стационарности VAR-модели:

. (2)

Корни уравнения (2) должны лежать за пределами единичной окружности для стационарной модели. Для нахождения коэффициентов модели используют метод наименьших квадратов.

Эта модель достаточно широко применяется в многомерных прогнозах макроэкономики как достаточно мощный и надежный инструмент. Сильной стороной VAR-модели является возможность отражения глубоких динамических свойств многомерных временных рядов. Известны результаты [2–4] использования данной модели, разработан математический аппарат, имеются программные реализации [5]. Исследования подтверждают, что существуют ограничения использования данного вида модели, которое заключается в требовании стационарности процесса y_t. Кроме того, VAR-модель плохо моделирует нелинейные структуры.

Нейросетевая модель основана на использовании аппарата искусственных нейронных сетей. По имеющимся выборкам данных строится и обучается нейронная сеть определенной архитектуры [6, 7]. Обученная нейронная сеть используется для прогнозирования будущих значений многомерного процесса [7].

Для построения прогнозирующей модели на нейронной сети не предъявляется требование стационарности процесса. Утверждается [8], что нейросети, являясь универсальным инструментом, способны выявлять нелинейные закономерности и взаимосвязи между компонентами многомерных случайных процессов. Экспериментальные исследования показывают перспективность данного вида моделей прогнозирования. Получены положительные практические результаты [9, 10]. Однако выбор структуры нейросетевой модели носит рекомендательный характер, что объясняется отсутствием строгой теории. Могут появляться проблемы при обучении сети. Поэтому существует необходимость проведения дополнительных исследований, сравнительного анализа прогнозирующих способностей различных нейросетевых структур.

ЛИТЕРАТУРА

1. Кругов В. В. Методы прогнозирования многомерных временных рядов / В.В.Круглов // Приборы и системы. Управление, контроль, диагностика. – 2005. - № 2. – С. 62-66.

2. Швайко П. Эконометрические модели анализа и прогнозирования емкости первичного рынка ГКО / П.Швайко // Эковест. – 2002. - № 2. – С. 111 – 153.

3. Стрижов В. В. Прогноз и управление в авторегрессионных моделях /
В. В. Стрижов, В. В. Шакин http://www.ccas.ru [Электронный ресурс].

4. Проблемы прогнозирования некоторых макроэкономических показателей / Р.М. Энтов [и др.] 28.11.2002 http://www.ie t.ru/publication.php [Электронный ресурс].

5. Карпов В. Э. Интеллектуальная система анализа макроэкономических показателей / В.Э.Карпов // Научная сессия МИФИ-2004: сб. науч. тр. - М, 2004. http://www.raai.org/about/persons/karpov/ [Электронный ресурс].

6. Заенцев И. В. Нейронные сети: основные модели / И.В.Заенцев. – Воронеж: Воронежский государственный университет, 1999.

7. Круглов В. В. Искусственные нейронные сети. Теория и практика / В. В. Круглов, В. В. Борисов. – М.: Горячая линия – Телеком, 2001.

8. Зубков А. В. Предсказание многомерных временных рядов с помощью нейросетей / А.В. Зубков // Информационные технологии - 2002. - № 2.

9. Пустарнакова Ю. А. Искусственная нейронная сеть как инструмент прогнозирования геологических параметров по сейсмическим атрибутам и данным бурения / Ю. А. Пустарнакова, Э.Р.Ахметова // Геофизика. – 2002. – С. 75-80.

10. Кащеев Д. Е. Построение трехмерной модели коллекторских свойств на основе стохастического анализа данных ГИС и сейсморазведки / Д. Е. Кащеев, Д. Г. Кирнос http://cge.ru/main/document/ [Электронный ресурс].

MODELS USED FOR MULTIVARIATE
STOCHASTIC FORECASTING

Petrova E. V.

The paper includes experience analysis of different models for multivariate stochastic forecasting. It discovers most perspective models – vectorial autoregression and neuronet model.

Кафедра информатики и электорадиотехники

Смоленский государственный университет

Поступила в редакцию 10.11.2006.