УДК 681.518

О ВЫБОРЕ МЕТОДОВ ПОСТРОЕНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ ДЛЯ ФОРМАЛИЗАЦИИ

ЗАДАЧ ПРИНЯТИЯ РЕШЕНИЙ

(zakharov.rar)

Ó 2006 г. Захаров В. А.

В статье рассмотрена проблема формализации задач принятия решений в условиях неопределенности. Одним из возможных путей решения указанной проблемы предлагается использование методического аппарата теории нечетких множеств, в частности – методов построения функций принадлежности. Приводятся правила обоснованного выбора конкретного метода (группы методов) построения функций принадлежности, адекватно представляющих формализуемую задачу принятия решений.

В общем случае принятие решения заключается [1]: в генерации возможных альтернатив решений {А}, их оценке и выборе лучшей («правильной») альтернативы А*. В результате оценки из исходного множества {А} выделяют подмножество альтернатив, допустимых по качеству {А^доп}, из которого по определенным критериям качества и выбирается лучший вариант. Часто уже при выработке исходного множества альтернатив, особенно при решении сложных задач при многих критериях, в исследуемом процессе могут принимать активное участие эксперты, как правило, это специалисты в данной предметной области, либо, при необходимости, в смежных (“критериальных”) областях. Структурное представление процесса принятия решений, включающего указанные этапы, показано на рисунке 1.

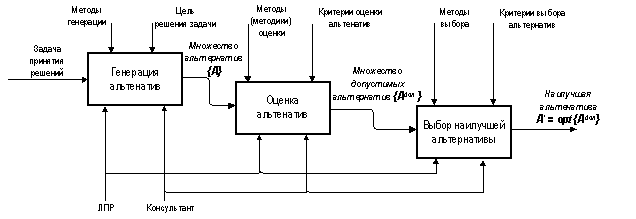
Рисунок 1 – Структурное представление процесса принятия решения

Принять «правильное» решение – значит, выбрать такую альтернативу из числа возможных, которая с учетом всех разнообразных факторов и противоречивых требований будет в максимальной степени способствовать достижению поставленной цели. Оптимальные решения позволяют достигать цели при минимальных затратах ресурсов [1].

Следовательно, в целях обеспечения оптимизации выбора лучшего варианта из имеющихся альтернатив их оценка должна учитывать влияние как отдельно каждого из указанных факторов на качество принимаемых решений, так и их комплексный/интегрированный учет в целом.

Однако, условия выработки и принятия решений, принимаемых должностными лицами органов управления, объективно усложняются необходимостью переработки постоянно возрастающих объемов информации в ограниченное время в условиях неопределенности обстановки. Используемая при этом исходная информация характеризуется неточностью, неполнотой и противоречивостью, что затрудняет принятие оперативных и обоснованных решений на управление.

В тоже время, принимаемые в процессе планирования решения и разрабатываемые планы должны быть обоснованными и обеспечивать наиболее полную реализацию возможностей подчиненных в текущих условиях обстановки.

Налицо противоречие между требуемыми качеством и оперативностью принимаемых решений, а также сроками и условиями их выработки и принятия и реализации.

Одним из путей повышения оперативности и качества принимаемых решений является автоматизация процесса выработки и принятия решений на основе методов и средств искусственного интеллекта в составе соответствующих экспертных систем и систем поддержки принятия решений. Построение моделей автоматизации процесса принятия решений для задач управления на основе экспертной информации, имеющих нечеткое описание, в составе систем поддержки принятия решения оказалось возможным благодаря введению понятий нечеткого множества и лингвистической переменной. В данных моделях результаты принятия управленческих решений могут приближаться по качеству к решениям, принятым человеком, а по скорости их получения существенно превышать время реакции человека (особенно в непредсказуемых и непредвиденных ситуациях) [2-5].

Для использования в моделях принятия решений информации, формализованной на основе теории нечетких множеств, необходимы процедуры построения соответствующих функций принадлежности. Построение последних является важным компонентом в формализации задач принятия решений. От того, насколько адекватно построенная функция отражает знания эксперта или экспертов, во многом зависит качество принимаемых решений.

Исходя из этого, для обработки и представления экспертной информации необходимо использовать специальные методы теории нечетких множеств и нечеткой логики. Для обеспечения обоснованного выбора конкретного метода (группы методов), адекватно представляющих формализуемую задачу принятия решений, необходимо провести их сравнительный анализ.

Следует отметить, что обработка и представление извлеченной экспертной информации о технологии решения задач принятия решений применительно к этапам рассматриваемого процесса может осуществляться посредством функций принадлежности и построения логико-лингвистических шкал различными способами, выбор которых зависит от того, какие цели преследуются данным процессом и в зависимости от вида задачи принятия решения. К таким способам относят две группы методов построения функций принадлежности: прямые и косвенные методы (рисунок 2) [5-6].

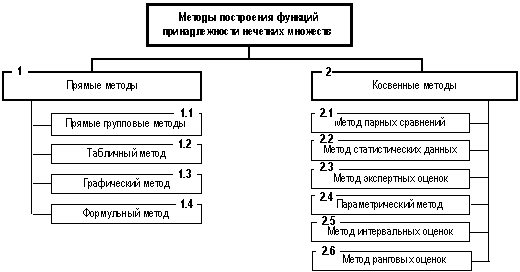
Рисунок 2 – Классификация методов построения функций принадлежности

нечетких множеств

Прямые методы характеризуются тем, что эксперт непосредственно задает правила определения значений функции принадлежности μ_А(х), характеризующей элемент х.

Эти значения согласуются с его предпочтениями на множестве элементов Х следующим образом [5, 6]:

1. Для любых х₁, х₂ Î Х μ_А(х₁) < μ_А(х₂) тогда и только тогда, когда х₂ предпочтительнее х₁, т.е. в большей степени характеризуется свойством А;

2. Для любых х₁, х₂ Î Х μ_А(х₁) = μ_А(х₂) тогда и только тогда, когда х₁ и х₂ безразличны относительно свойства А.

Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давление, температура и т.д., или когда выделяются полярные значения.

Разновидностями прямых методов являются прямые групповые методы, когда, например, группе экспертов предъявляют конкретный объект, и каждый должен дать один из двух ответов: принадлежит или нет этот объект к заданному множеству. Тогда число утвердительных ответов, деленное на общее число экспертов, дает значение функции принадлежности объекта к данному нечеткому множеству.

Прямыми методами являются также непосредственное задание функции принадлежности таблицей, графиком или формулой.

Из анализа результатов исследований и решения практических задач, связанных с необходимостью обрабатывать информацию, известно, что прямые методы в основном используются в качестве вспомогательных, т. к. характеризуются большой долей субъективизма [1, 4-5].

Косвенные методы построения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяются нечеткие множества.

В косвенных методах значения функции принадлежности выбираются таким образом, чтобы удовлетворить заранее сформулированным условиям. Экспертная информация является только исходной информацией для дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру ее обработки. К таким методам относятся статистический метод, метод парных сравнений, метод экспертных оценок и ряд других. Далее рассмотрены наиболее часто используемые методы.

Метод построения функции принадлежности на основе парных сравнений основан на обработке матриц оценок, отражающих мнение эксперта об относительной принадлежности элементов множеству или степени выраженности у них свойства, формализуемого множеством [5].

Степень принадлежности элементов множеству определяется посредством парных сравнений. Для сравнения элементов используются оценки, приведенные в таблице 1.

Из результатов анализа различных источников [1-5] следует, что рассмотренный метод может использоваться как для решения задач выработки альтернатив, так и для их сравнения и выбора лучшей из них.

Таблица 1 – Шкала для определения матрицы суждения

Оценка важности	Качественная оценка	Примечание
1	Одинаковая значимость	По данному критерию альтернативы имеют одинаковый ранг
3	Слабое превосходство	Соображения о предпочтении одной альтернативы перед другой малоубедительной
5	Сильное (или существенное) превосходство	Имеются надежные доказательства существенного превосходства одной альтернативы
7	Очевидное превосходство	Существуют убедительные свидетельства в пользу одной альтернативы
9	Абсолютное превосходство	Свидетельство в пользу предпочтения одной альтернативы перед другой в высшей степени убедительно
2, 4, 6, 8	Промежуточные значения между соседними оценками	Используются, когда необходим компромисс

Метод статистических данных основан на обработке статистической информации. В качестве степени принадлежности элемента множеству принимается оценка частоты использования понятия, задаваемого нечетким множеством, для характеристики элемента. При использовании специальных матриц подсказок получаются функции принадлежности [5].

На универсальной шкале [0, 1] необходимо разместить значения лингвистической переменной: ОЧЕНЬ МАЛО, МАЛО, СРЕДНЕ, МНОГО, ОЧЕНЬ МНОГО. Тогда степень принадлежности некоторого значения вычисляется как отношение числа экспериментов, в которых оно встречалось в определенном интервале шкалы, к максимальному для этого значения числу экспериментов по всем интервалам. Метод основывается на условии, что в каждый интервал шкалы попадает одинаковое число экспериментов. Это условие часто не соблюдается. В реальных случаях составляется эмпирическая таблица, в которой эксперименты могут быть распределены неравномерно по интервалам, а в некоторые интервалы могут вообще не попасть.

Данный метод может быть использован для формализации задачи выбора альтернатив, т. к. эксперты могут определить конкретное множество допустимых альтернатив и удалить не нужные. В данном случае оценки отдельных экспертов можно рассматривать как независимые реализации случайной величины.

Построение функции принадлежности на основе экспертных оценок [5].

Данный метод построения функций принадлежности основан на использовании нечетких чисел, приблизительно равных некоторому четкому числу, и приближенных интервальных оценок, отражающих мнения экспертов по рассматриваемому вопросу. Задача сводится к отысканию параметров заранее заданной (экспоненциальной) функции, при решении которой используются результаты экспертного опроса.

Из анализа различных источников [1-5], посвященных методам построения функций принадлежности, данный метод целесообразнее всего использовать при решении задач выработки и оценки альтернатив.

Построение функций принадлежности на основе интервальных оценок. Данный метод применяется для формализованного представления задач выбора, в которых отсутствует четкая грань между допустимым и недопустимым (в пространстве неуправляемых параметров) и между идеальным и неудовлетворительным состояниями (в пространстве критериев) [5].

Исходя из анализа сущности и содержания рассмотренных методов, могут быть сформулированы общие рекомендации по их практическому использованию при построении функций принадлежности нечетких множеств, отражающих формализованное представление рассмотренных задач принятия решений.

Таким образом, можно установить соответствие между методами построения функций принадлежности и задачами принятия решений.

Основой для решения задачи определения соответствия между указанными методами и задачами принятия решений являются групповые мнения экспертов в области теории принятия решений.

Для практической проверки выдвинутой идеи был проведен опрос десяти экспертов с задачей, в интервале от 0 до 1, указать степень соответствия каждого метода – каждой задаче рассматриваемого процесса.

Выборочные результаты опроса представлены в таблице 2.

Таблица 2 – Фрагмент результатов экспертных оценок соответствия между методами построения функций принадлежности и задачами принятия решения

методы построения функций принадлежности/ задачи принятия решений	Задача выработки альтернатив	Задача оценки альтернатив	Задача выбора альтернатив
Метод парных сравнений	0,85	0,5	0,9
Метод статистических данных	0,6	0,5	0,85
…	…	…	…
Метод ранговых оценок	0,45	0,75	0,68

Полученные соответствия позволяют сформулировать правила выбора методов построения функций принадлежности применительно к рассматриваемым задачам принятия решений.

Для выбора методов для формализованного представления рассмотренных задач правила должны иметь вид:

П^ФПЗ: если х₁ есть Z_n, то у₁ есть М = {M_k}, n = 1, …, N,

где	П^ФПЗ	–	правило выбора методы при решении соответствующей задачи;
	х1	–	входная переменная (наименование задачи);
	у1	–	переменная вывода (перечень методов построения функций принадлежности);
	Zn	–	задача принятия решений;
	М^О	–	множество методов построения функций принадлежности, отобранных по условию предпочтения и со значением уровня соответствия большем или равным 0,5.

Таким образом, проблема выбора методов построения функций принадлежности для формализации рассматриваемых задач решается с помощью предложенных правил, что позволяет учитывать, как правило, вид решаемой задачи, сложность получения экспертной информации для ее решения, достоверность экспертной информации, а также трудоемкость алгоритма обработки информации при построении функции принадлежности.

Литература

1. Вилкас Э. Й., Майминас Е. З. Решения: теория, информация, моделирование. – М., Радио и связь, 1981.

2. Борисов А.Н., Алексеев А.В., Меркурьев Г.В. и др. Обработка нечеткой информации в системах принятия решений. – М., Радио и связь, 1989.

3. Аверкин А. Н., Батыршин И. З., Блишун А. Ф. и др. Нечеткие множества в моделях управления и искусственного интеллекта. – М., Наука, 1986.

4. Кофман А. Введение в теорию нечетких множеств. – М., Радио и связь, 1982.

5. Борисов А.Н., Крумберг О.А., Федоров И.П. Принятие решения на основе нечетких моделей: примеры использования. – Рига, ”Знание”, 1990, 184 с.

6. Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теория и практика. – М., Горячая линия – Телеком, 2001.

MEMBERSHIP FUNCTIONS CONSTRUCTION CHOICE FOR DECISION

PROBLEMS FORMALIZATION

Zakharov V. A.

This article consider problem of decision-making tasks formalization in conditions of uncertainty. As a basis for specified problem solution the fuzzy-set theory methodical apparatus are proposed, in particular. The rules membership functions construction methods (group of methods) choice adequately representing a formalization task of acceptance of decisions are considered.

Лаборатория специального математического и программного обеспечения (СМПО)

Научно-исследовательский центр (НИЦ) ВА В ПВО ВС РФ

Поступила в редакцию 15.09.2006.