УДК 681.3

Решение задачи согласования критериев при построении нечёткой оценочной модели

(zernov.rar)

Ó 2006 г. Зернов М. М. (Photo)

В данной статье предлагается способ построения многокритериальной оценочной модели некоторой системы на основе нечёткого подхода. Описывается процедура формализации предметной области, позволяющая учесть и согласовать различные критерии качества – цели функционирования системы. Предлагается гибкий алгоритм получения обобщённой оценки состояния системы на основе оценок по частным критериям, адаптируемый под различные трактовки согласованности критериев. В основу алгоритма положен поиск полного подграфа максимальной величины в отображении общего графового представления совокупности критериев на некоторую степень согласованности.

1. Постановка задачи нечёткого многокритериального оценивания

Для большого класса задач управления необходимо оценивать возможное состояние управляемой системы. При этом выбор управленческого решения или последовательности решений зависит от оценки текущего состояния системы и его прогноза.

Задача оценивания состояния системы требует построения оценочной модели, позволяющей получить обобщённую оценку состояния на основе ряда разнородных критериев и показателей качества – целей функционирования системы. Обобщение показателей качества возможно различными способами, каждый из которых имеет свои преимущества и недостатки.

В настоящее время все более широкое распространение получают способы оценки, основанные на нечётком подходе. Основными достоинствами нечётких оценочных моделей являются:

· возможность гибкого объединения разнородных критериев;

· возможность формулировать правила оценки в терминах естественного языка.

Последнее обстоятельство позволяет описывать практически бесконечное число состояний системы конечным множеством термов.

В соответствии с нечётким подходом, в общем виде задача ставится следующим образом. Имеется набор критериев качества , каждый из которых отражает некоторую цель функционирования системы. Применяя каждый из критериев к оцениваемому объекту, получаем частную оценку объекта по данному критерию . При нечётком подходе данная оценка выражается числом в диапазоне [0, 1] и характеризует степень выполнения критерия. Степень выполнения критерия по каждому объекту можно трактовать как значение функции принадлежности рассматриваемого объекта множеству объектов, совместимых с указанной частной целью (удовлетворяющих рассматриваемому критерию): ,где – общее множество объектов. Требуется на основании совокупности , получить некоторое значение – степень выполнения обобщённого критерия [2]. К отображению h предъявляются требования нормировки, неубывания, непрерывности. Часто к требованиям добавляют свойство ассоциативности, зачастую невыполнимое на практике, и заменяемое требованием бисимметричности.

Таким образом, описанную задачу условно можно разделить на два этапа: получение оценок степени выполнения частных критериев и получение обобщённой оценки объекта.

Первый этап реализуется обычно за счёт известных систем нечёткого продукционного вывода и достаточно хорошо изучен [1]. Второй этап обладает рядом специфических особенностей.

К оценочным моделям сложных систем предъявляются следующие требования:

· возможность формирования общего критерия на основе изменяющихся наборов частных критериев;

· простая перенастройка модели при добавлении нового критерия;

· учёт согласованности частных критериев;

· учёт различной значимости частных критериев в обобщённой оценке и обеспечение её перенастройки.

Проблема согласованности частных критериев заключатся в том, что на практике одновременное достижение двух и более целей обычно невозможно, ввиду их противоречивости. Эксперт, предоставляющий сведения о системе, при оценке объекта, характеризующегося противоречивыми критериями, руководствуется некоторой стратегией оценки, экстремальными вариантами которой в 2-местном случае являются: одновременное достижение целей (соответствует операция ) и достижение одной цели (соответствует операция ).

Существует большое множество двуместных операций h, реализующих стратегии, характеризующие различные степени одновременного достижения целей. Связка h может быть представлена как некоторой аналитической свёрткой (min, max, med), так и некоторой системой нечёткого вывода. Определение стратегии попарного объединения критериев проводится, прежде всего, на основе экспертного опроса. При этом говорят, что пары целей, для которых эксперт применяет одинаковые стратегии оценки, согласованы с некоторой одинаковой степенью согласованности.

Значимость критериев может многократно меняться с течением времени, её учёт, как правило, осуществляется путём настройки весов критериев и введения их в отображение h , определённое для равнозначных критериев как параметров на этапе функционирования модели [2]. Процедуры определения весовых коэффициентов известны [1].

2. Способ формализации предметной области при формировании
нечёткой оценочной модели

Модель оценки строится на основе информации о предметной области, получаемой от эксперта или других достаточно достоверных источников. Ниже предложен вариант способа формализации информации о предметной области при построении нечёткой многокритериальной оценочной модели.

Весь процесс формализации предметной области можно разделить на следующие основные этапы.

1. Построение максимально полного списка всех возможных частных целей и выделение, в случае необходимости, наиболее значимых из них.

2. Определение согласованности целей из списка между собой.

Данный этап можно реализовывать, как определяя степени попарной согласованности частных целей непосредственно, так и описывая уровни согласованности для пар абстрактных целей с последующим указанием уровня согласованности для каждой пары целей из списка. Второй вариант повышает нагрузку на эксперта, но увеличивает гибкость системы при появлении непредусмотренных целей. Компромиссный вариант предусматривает описание уровней согласованности на примере одной или нескольких пар критериев из списка и распространение данного описания на остальные пары критериев.

В зависимости от предметной области и точки зрения эксперта на проблему, согласованность может пониматься по-разному (“корреляция”, “взаимовлияние”, “одновременная достижимость”). Практически любую трактовку согласованности можно свести к ответу на вопрос о возможности одновременного принятия критериями характерных значений (“низкий”, “средний”, “высокий” и т.д.), соответствующих чётким (точечным) или нечётким (интервальным) значениям на отрезке [0, 1]. В результате описание некоторой степени согласованности даётся в виде таблицы, в которой отмечены возможные сочетания значений критериев. Указание же степеней согласованности для пар критериев предполагается осуществлять с помощью матрицы согласованности, содержащей цифровые обозначения степеней согласованности для каждой пары; при этом вид матрицы (симметричная/несимметричная) зависит от принятой трактовки согласованности. Примеры матрицы согласованности и таблицы сочетаний представлены в таблицах 1 и 2.

Таблица 1

Пример матрицы согласованности

	1	2	3	4	5
Критерий 1	-	3	3	2	3
Критерий 2	3	-	3	1	2
Критерий 3	3	3	-	2	2
Критерий 4	2	1	2	-	1
Критерий 5	3	2	2	1	-

1 – “плохая согласованность”, 2 – “средняя согласованность”, 3 – “хорошая согласованность”

Таблица 2

Пример таблицы сочетаний значений критериев

“хорошая согласованность”	отл	хор	уд	пл
Отл	x	x	x
Хор	x	x	x
Уд		x	x	x
Пл			x	x

3. Определение стратегий, принятых экспертом для различных уровней согласованности (цели считаются условно равнозначными) и построение связок, их реализующих.

Опрос на данном этапе, как и на предыдущем, может проводиться как на абстрактных, так и на предметных критериях (или по компромиссному варианту). При этом следует избегать установления различной значимости критериев экспертом в ситуации их условной равнозначности.

В идеальном случае эксперт прямо указывает свёртку, соответствующую некоторой степени согласованности. Однако в большинстве случаев связку приходится идентифицировать [3]. Исходным материалом для идентификации служит оценочная таблица, составляемая следующим образом: берётся соответствующая таблица сочетаний значений критериев и для каждого отмеченного возможного сочетания значений проставляется его оценка. Пример оценочной таблицы приведен в таблице 3. Вид оценочных таблиц определяет характер операций попарного объединения оценок, а значит и всего алгоритма получения обобщённой оценки. В том случае, если таблица имеет пустые элементы (неполная таблица), она считается несимметричной, когда в ней присутствует пара симметричных относительно главной диагонали непустых элементов, значения которых отличны друг от друга.

Возможны следующие варианты:

· таблица симметрична относительно главной диагонали – тогда порядок следования операндов в связке не важен;

· таблица несимметрична – в данном случае приходится учитывать порядок следования операндов.

Практически все аналитические свёртки – симметричны. Поэтому в случае несимметричных таблиц связку h приходится строить в виде некоторой системы нечёткого логического вывода на основе оценочной таблицы.

Связки можно определять не только для пар критериев, но и для большего их числа.

В результате для каждой степени согласованности определяется операция-связка, позволяющая объединить значения оценок по частным критериям, которая может быть представлена как некоторой аналитической свёрткой, идентифицированной по оценочной таблице, так и системой нечёткого логического вывода.

Таблица 3

Пример оценочной таблицы (соответствует свёртке min)

“хорошая согласованность”	Отл	Хор	Уд	Пл
Отл	Отл	Хор	Уд
Хор	Хор	Хор	Уд
Уд		Уд	Уд	Пл
Пл			Пл	Пл

4. Проверка полученных описаний на ошибки. Поиск конфликтов в матрице согласованности. Устранение ошибок и конфликтов.

Как на этапе определения согласованности, так и на этапе определения стратегии оценивания, принятой экспертом, следует проводить контроль данных, предоставляемых экспертом. Такой контроль можно провести как за счёт анализа сформированных описаний, так и с использованием проверочных примеров. Признаками ошибки могут служить:

· одинаковые таблицы для различных степеней согласованности,

· различные результаты по парам критериев, для которых указаны одинаковые степени согласованности;

· несимметричность оценочных таблиц (если данная несимметричность не обусловлена сознательным представлением о характере операции объединения значений);

· несоответствие смысловой трактовки степени согласованности и результата опроса – примером может служить усиление требований к одновременному достижению целей по мере ухудшения их согласованности.

Также поможет найти противоречия перебор всех всевозможных значений критериев, используемых при составлении описания. Второй этап формализации предметной области естественным образом накладывает ограничения на возможные сочетания значений частных критериев. Признаком ошибки может служить отсутствие какого-либо значения любого из критериев среди разрешённых сочетаний значений. В случае обнаружения ошибки возможен возврат к любому из предшествующих этапов с целью её устранения.

Конфликтом будем называть ситуацию, при которой для некоторой пары критериев эксперт указывает различные степени согласованности в зависимости от порядка следования критериев. Данной ситуации соответствует такое отклонение от симметрии матрицы согласованности, при котором значения симметричных относительно главной диагонали элементов отличны от 0 и друг от друга. В этом случае возможно два решения проблемы:

· если оценочные таблицы симметричны – следует выбрать один из элементов и приравнять к нему другой;

· в противном случае следует выбрать один из элементов, а другой приравнять к нулю, установив, таким образом, направление связи, соответствующее порядку следования операндов в парной связке.

Результатами процедуры формализации предметной области являются:

· список частных критериев;

· матрица согласованности критериев (соответствующая ненаправленной или направленной интерпретации согласованности);

· набор операций – связок, соответствующих степеням согласованности и позволяющих проводить попарное (или многоместное) объединение значений оценок критериев.

В случае внезапного возникновения новых частных целей, предложенная процедура формализации предметной области позволяет быстро перенастроить модель, увеличив размерность матрицы согласованности критериев и указав ссылки на степени согласованности нового критерия с уже имеющимися.

3. Алгоритм получения обобщённой оценки состояния системы

Наиболее сложной задачей является определение на основе частных операций (для 2-местного варианта) и весовых коэффициентов критериев общей операции обобщения оценки .

Для её решения предлагается следующий алгоритм.

Итак, пусть имеем набор степеней согласованности критериев, обозначенных натуральными числами и упорядоченными в порядке возрастания согласованности критериев:

Предположим, что удалось указать попарные степени согласованности частных критериев и интерпретировать их в виде некоторых операций , удовлетворяющих представленным выше требованиям. Поскольку операции определялись для случая равнозначных критериев, с целью получения корректной оценки входные данные следует дополнить вектором весовых коэффициентов:

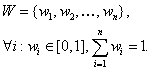
Таким образом, исходные данные можно представить в виде графа размера n:

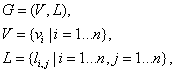
вершины которого характеризуются тройкой:,

а дуги взвешены значениями степеней согласованности .

Если из рассмотрения исключаются некоторые критерии качества, то соответствующие им вершины просто не включаются в граф V.

В случае если все операции (для 2-х аргументов) симметричны, т.е. , имеем дело с взвешенным неориентированным графом, в противном случае граф ориентированный. Рассмотрим вначале случай ненаправленного графа. Граф, соответствующий матрице согласованности, представленной в таблице 1, и вектору весовых коэффициентов изображён на рисунке 1.

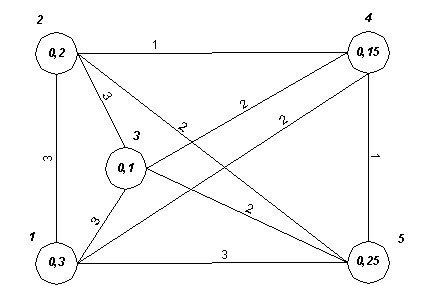
Рисунок 1 – Пример графа, соответствующего матрице согласованности, представленной в таблице 1

Предлагаемый алгоритм получения обобщённой оценки состояния системы основан на поиске полного подграфа максимальной величины, в котором все дуги взвешены одинаковым значением: .

Общая структура алгоритма получения обобщённой оценки включает следующие основные этапы.

1. Определение порядка просмотра степеней согласованности критериев (по возрастанию/убыванию), выбор начальной рассматриваемой степени согласованности . Пусть для определённости выбран обратный порядок рассмотрения степеней согласованности, тогда номер текущей степени согласованности и .

2. Получение отображения графа G на степень согласованности – из множества рёбер оставляем только те, которые взвешены значением :

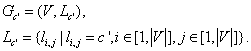
Отображение графа рассматриваемого примера на степень согласованности “3 – хорошая согласованность” представлено на рисунке 2.

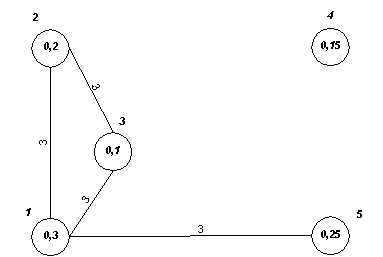
Рисунок 2 – Отображение графа примера на степень согласованности

“3 – хорошая согласованность” (вершины-кандидаты на объединение: 1, 2, 3)

3. Устанавливаем начальную величину искомого подграфа по числу вершин общего графа.

4. Формируем все всевозможные подграфы размерности M: .

5. Если среди подграфов нет ни одного удовлетворяющих условию полноты: ,

то уменьшаем размер искомого подграфа , и если он более единицы, то возвращаемся к 4-му этапу.

Если , переходим к этапу 7.

Если же среди полученных подграфов есть полные, переходим к этапу 5.

6. Сортируем полные подграфы размерности M в порядке убывания суммарного веса, входящих в них вершин (можно установить и иной порядок просмотра подграфов). Последовательно проходя данные подграфы, сворачиваем их вершины в одну посредством операции , соответствующей рассматриваемой степени согласованности . Пусть рассматривается полный подграф . Тогда из общего множества вершин удаляются сворачиваемые вершины: и добавляется некоторая новая сформированная вершина , ассоциируемая с некоторым объединённым критерием , получающая некоторый свободный номер r:. Из множества рёбер подграфа удаляются все, связанные с удаляемыми вершинами и определяются веса дуг, связанных с новой вершиной: . Вершины объединяются только один раз и в том случае, если множества вершин полных подграфов пересекаются – сворачивается тот, суммарный вес которого больше. Подробнее данный этап алгоритма будет рассмотрен ниже. По завершении обработки уменьшаем размер искомых подграфов с учётом нового количества вершин и если он больше единицы переходим к этапу 4. Если , то переходим к этапу 7. На рисунке 3 представлен результат объединения вершин единственного полного подграфа размерности 3 для рассматриваемого примера (рассматривается степень согласованности “3 – хорошая согласованность”).

7. Проверяем условие прекращения работы алгоритма: . Если оно выполняется, то возвращаем в качестве итоговой оценки величину единственной вершины . Иначе – изменяем номер текущей степени согласованности и , после чего возвращаемся ко 2-му этапу алгоритма.

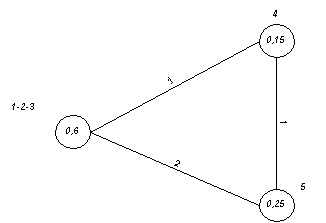
Рисунок 3 – Результат первого объединения вершин графа

Рассмотрим подробнее способы формирования вершины из некоторого подграфа размерности M и определения её связей с другими вершинами .

Как уже упоминалось, – некоторый абстрактный объединённый критерий, дающий имя вершине, и образуемый перечислением объединяемых критериев . Вес новой вершины является суммарным весом объединяемых вершин: .

Наибольший интерес вызывает получение значения оценки по объединённому критерию . Способ получения данного значения зависит от трактовки степени согласованности в виде операции . Для удобства переобозначим вершины: .

Операция это некоторая функция от 2-х переменных с областью определения и областью значений , позволяющая учитывать веса сворачиваемых значений. В дальнейшем для краткости в качестве аргументов будем указывать только оценки по критериям, подразумевая при этом, что веса критериев также являются аргументами операции .

Проще всего определяется в случае, если – операция, расширяемая на M аргументов. В этом случае . В том случае, если операция не ассоциативна, то следует установить порядок перечисления аргументов, например, по убыванию весов.

В том случае, если операция не расширяется на большее число аргументов, следует определить порядок попарного сворачивания вершин. Опять же можно начинать с вершин, обладающих наибольшим весом. Тогда полагая, что , получим для случая симметричной операции :

.

Пусть нам нужно определить связи вершины с некоторой вершиной :. Учитывая неориентированный характер графа: , связь определяется как некоторая целочисленная функция от всех связей между объединяемыми вершиной и . Вид функции f – определяется предпочтениями эксперта и является ещё одним настраиваемым параметром алгоритма, позволяющим варьировать желаемую степень одновременного достижения целей, вошедших в объединённую вершину и не вошедших в неё. Для рассматриваемого примера в качестве f будем использовать: .

Ситуация значительно усложняется, если – двуместная несимметричная операция. Тогда граф становится ориентированным. При этом условие полноты подграфа, заменяется условием: (наличие связи по указанной степени согласованности хотя бы в одну сторону).

Возникает проблема определения как направления связи между объединённой вершиной и некоторой вершиной , так и порядка следования аргументов при объединении вершин. Предлагаются следующие варианты разрешения данных проблем.

При определении направления указанной связи вначале определяем значение степени согласованности, отвечающей за данную связь. Как и ранее будем использовать функцию min, но вести подсчёт по входящим и исходящим дугам: . Далее считаем количество дуг, взвешенных степенью , входящих в вершину из вершин множества и исходящих из неё в вершины того же множества – и . В зависимости от соотношения принимаем направление результирующей дуги, как это показано на рисунках 4–6.

В случае равенства количества входящих-исходящих дуг направление определяем по соотношению весов и. Если дуга входит в , то принимаем , а и наоборот.

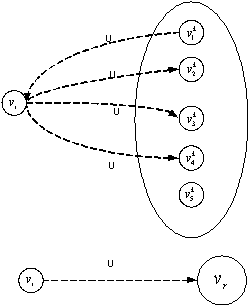
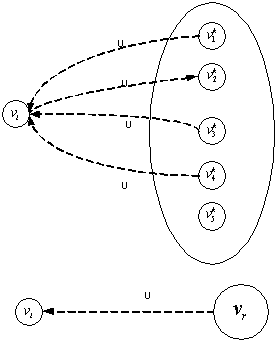
Рисунок 4 – Определение направления Рисунок 5 – Определение направления связи для случая связи для случая

Подобным образом определяется и порядок следования аргументов в попарных свёртках.

В результате предложенный алгоритм получения обобщённой оценки состояния системы позволяет сочетать различные операции объединения оценок частных критериев, гибко адаптируясь к условиям конкретной предметной области.

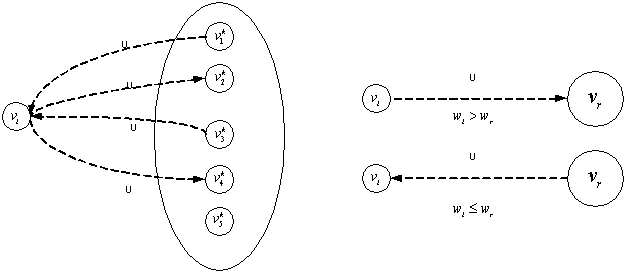
Рисунок 6 – Определение направления связи для случая

4. Заключение

Предложенный способ построения нечёткой многокритериальной оценочной модели позволяет построить гибкую оценочную модель, учитывающую как неравнозначность и противоречивость частных целей, так и трактовку согласованности целей, соответствующую предметной области.

Предложенный алгоритм получения обобщённой оценки состояния системы конструирует операцию обобщения оценки системы на основе ряда более простых операций, соответствующих степеням согласованности частных целей.

Способ формализации предметной области и алгоритм получения обобщенной оценки обеспечивают гибкую перенастройку модели как при изменении состава критериев качества, так и их значимости.

Литература

1. Андрейчиков А.В., Андрейчикова О.Н. Анализ, синтез, планирование решений в экономике. – М.: Финансы и статистика, 2001.

2. Борисов В.В., Бычков И.А., Деменьтьев А.В., Соловьёв А.П., Федулов А.С. Компьютерная поддержка сложных организационно-технических систем. – М.: Горячая линия – Телеком, 2002.

3. Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний и информатике: Пер. с фр. – М.: Радио и связь, 1990.

solution of the problem of the criterion

co-ordination upon fuzzy estimate MODEL CONSTRUCTION

Zernov M. M.

The kind of fuzzy based multicriteria estimate model construction procedure is offered in this article. The way of subject model formalization, which allows taking into account and coordinating different quality criteria – the system operating purposes, is described. The flexible algorithm of generalized estimate obtaining, adaptable for different criteria consensus interpretations, is offered. The algorithm is based on searching of a full subgraph of maximum size in a projection of criteria set generalized graph representation on some consensus degree.

Кафедра вычислительной техники

Филиал ГОУВПО «Московский энергетический институт (технический университет)» в г. Смоленске

Поступила в редакцию 15.09.2006.