УДК 611(081)

Суставы поддаются такому точному и всестороннему исследованию, механизм деятельности, связанный с их строением, имеет такое широкое и существенное значение при изучении строения организма человека и позвоночных животных вообще, что приходится удивляться, как могут анатомы до сих пор придерживаться описательного метода преподавания. Спрашивается, какую пользу приносит описательное преподавание для выяснения формы и строения человеческого организма? Ответ на этот вопрос дает нам современное состояние медицины, педагогики и других прикладных предметов. Страшная за новыми фармацевтическими средствами лечения, отсутствие всякого анатомического анализа, а вместе с этим полное невнимание к выяснению форм и их связи с нормальными отправлениями организма показывают, как трудно развиваются прикладные предметы, если предметы, служащие их основанием, не изучаются научным путем и не имеют никакого отношения к выяснению жизненных явлений. Что может дать описание мертвых форм, обозначенных разнообразными названиями, чуждыми изучающему? Между тем изучение форм, как, например, суставов, уже в настоящее время поддается такому точному, логическому изучению и последовательному анализу, что является возможность говорить о теории, или философии, суставов. Действительно, геометрические формы суставных поверхностей так логически связаны с отправлениями суставов, что по анализу формы можно определить все существующие в суставе движения, и обратно, по движениям, наблюдаемым у живого, можно с математической точностью определить форму, лежащую в основании этого движения.

При изучении суставов приходится постоянно убеждаться, что существующие в них движения соответствуют движению образовательной линии для данной геометрической формы суставной поверхности [2]. Неподвижная линия, вокруг которой образовательная движется, составляет ось сустава. В связи с расположением данной оси расположены связки, окружающие сустав. Каждую ось пересекает под прямым углом равнодействующая расположенных здесь мышц, тип которых находится в прямой зависимости от формы и величины движения; в логической связи с типичной формой мышц находятся существующие здесь сосуды и нервы. Все это так тесно и логически связано и прямо определяется из наблюдений над жизнью организма, что приходится поражаться, каким образом преподаватели анатомии могут оставлять без внимания все эти строго научно выработанные выводы относительно деятельности суставов и ограничиваться одним описанием, не имеющим научного значения и не выясняющим жизненных проявлений.

Приступая в настоящее время к выяснению теории простых суставов, необходимо отличить: 1) наблюдение деятельности сустава в живом организме, исследование и проверку при посредстве опыта и 2) математический анализ, выясняющий значение существующих здесь форм и величину оказываемого ими сопротивления.

Разработку последнего отдела любезно взял на себя профессор И. П. Долбня, исследования которого приведены ниже.

Простые суставы могут быть только двух видов: 1) с поверхностью вращения, образованной около одной оси, и 2) с поверхностью, образованной движением вокруг всевозможных осей, проложенных через один общий центр.

Они бывают цилиндрическими, конусовидными, эллиптическими, параболическими, гиперболическими поверхностями или с поверхностями, образованными различными кривыми при их вращении вокруг одной оси. Все эти поверхности в связи с различием геометрической формы различаются между собой еще тем, что при одинаковых линейных размерах представляют поверхности различной величины; таким образом, различные геометрические формы представляют собой при одинаковых линейных размерах опору различной величины, а вместе с этим различие в степени проявления сил. В этом легко убедиться, приняв во внимание качество образовательной линии; так, тело с цилиндрической поверхностью, образовательная которой представляет прямую линию, составляющую кратчайшее расстояние между двумя точками, вместе с этим представляет также и наименьшую опору для данного размера. Поверхность опоры несколько увеличивается, если образовательная наклонная линия и, следовательно, форма поверхности конусообразная. Еще более увеличивается поверхность опоры, если образовательная полуэллипсис; увеличение будет прогрессировать при движении образовательной в виде полупараболы, далее - полукруга или полугиперболы. Соотношения между этими поверхностями были первоначально установлены наблюдениями над суставами с движением вокруг оси. Оказывается, что так называемые блоковидные суставы всего чаще являются у тех животных, у которых движения наименее разнообразны, т. е. у которых существуют только сгибание и разгибание. Эти движения на самом деле таковы, что при производстве их принимает участие наибольшее число мышечных групп, окружающих сустав; так что, если через центр сустава проложить фронтальную плоскость, то все мышечные группы, лежащие с вогнутой стороны такого сустава, будут участвовать при сгибании, точно также, как все группы, расположенные по другую сторону этой плоскости, т. е. с выпуклой стороны сустава, будут мышцами разгибающими.

Для проверки приведенного положения проф. И. П. Долбня подверг математическому анализу поверхности эллипсоида, параболоида и гипперболоида вращения, а также поверхности шара, заданных определенными сходными условиями. Исследования эти заключаются в следующем.

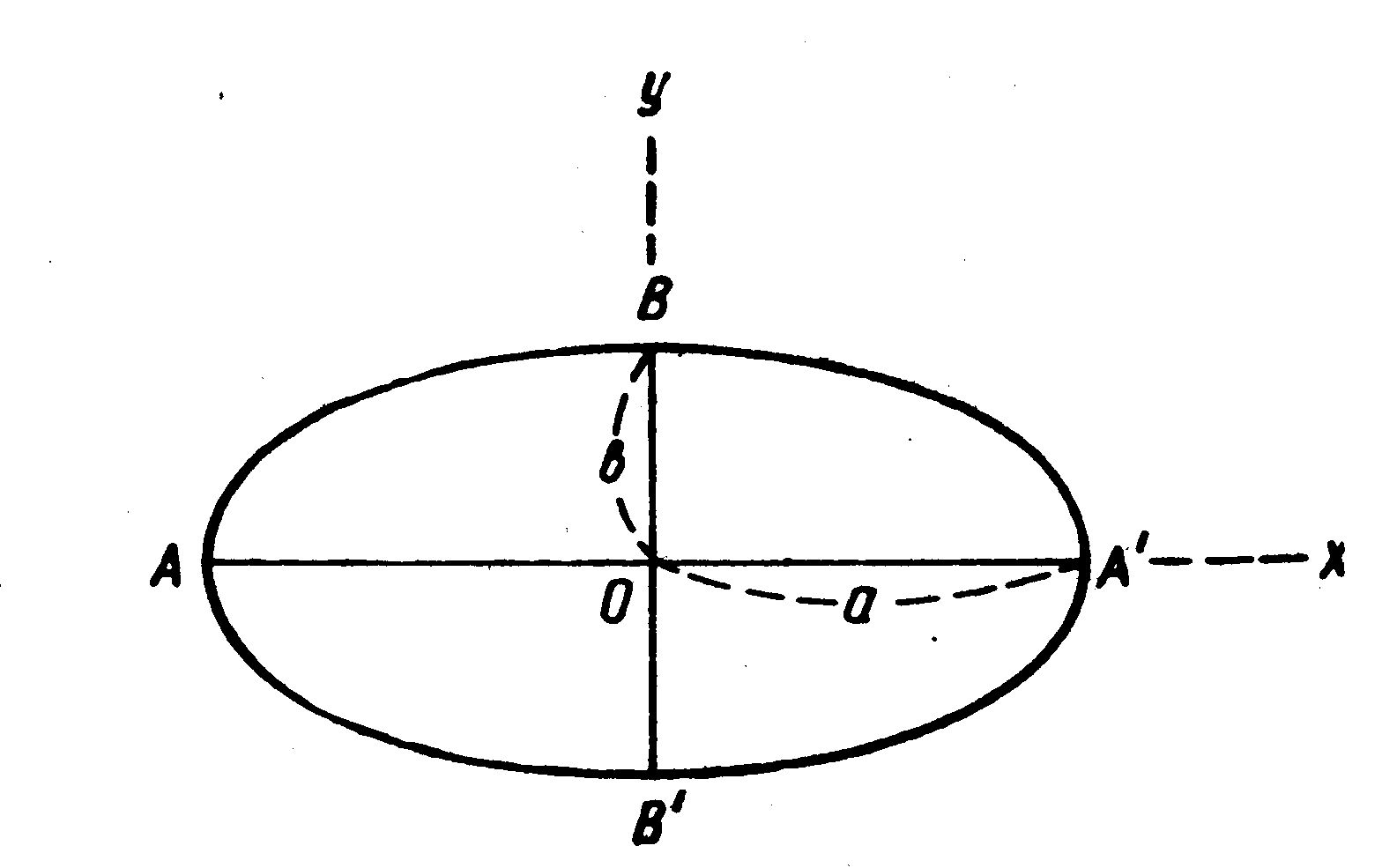
В этой статье предстоит подвергнуть численной оценке поверхности вращения, обладающие одинаковыми линейными размерами. Для сравнения берутся следующие поверхности: 1) эллипсоид вращения (рис. 1), оси которого AA' и BB' находятся в отношении 2:1; 2) гиперболоид вращения (рис. 2), главные размеры которого AO и AB находятся с горлом Og в том же отношении 2:1; 3) параболоид вращения (рис. 3), обладающий такими же главными размерами и таким же горлом, как и гиперболоид; наконец, 4) шар, радиус которого есть средняя арифметическая между главными размерами эллипсоида. Упомянутые здесь поверхности вычислены по обычным правилам начал интегрального исчисления. Автор совершенно устранил общие формулы и все вычисления довел до конца, пользуясь логарифмическими таблицами Вега. Имея в виду, что для научных целей, для которых предназначалась выкладка, не нужна очень большая точность, автор ограничился вычислением трех десятичных знаков; но легко понять, что степень точности выкладки может быть увеличена по произволу.

§I. Эллипсоид вращения

Дается эллипс (рис. 1)

        или

Называя эксцентриситет

Искомая поверхность выразится интегралом

Поэтому

и мы получим

§II. Гипербола вращения

Дается гипербола (рис. 2)

Рис. 1. Объяснение в тексте

Гипербола вращения около мнимой оси 0y. Требуется вычеслить поверхность вращения GDCD по следующим данным: b=OD=1; k=AO=AB=2.

Элемент поверхности будет

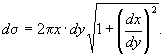
Из уравнения (4)

поэтому

Поверхность S_h выразится интегралом

где

Найдем теперь интеграл

Имеем:

Следовательно

Поэтому

В этой формуле имеем b=1, k=AB=2.

Точка B (2,2) лежит на гиперболе

поэтому

§III. Параболоид вращения

Дается парабола (рис. 3)

Рис. 3. Объяснения в тексте.

на которой лежит точка А (1,2); следовательно: 2p=4, p=2; y² =4x..

Перенесем начало координат в точку O(-1,0).

Уравнение параболы будет

Парабола вращается около оси y.

Элемент поверхности вращения выразится формулой

Из уравнения параболы имеем

Следовательно:

или

или

Поверхность параболоида вращения будет

Полагая

имеем

или

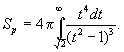
Разлагая дробь

на элементы, получим

Следовательно:

или

На этом основании

или

§IV.

Для сравнения с найденными кривыми поверхностями берется шар, радиус которого есть средняя арифметическая между главными размерами эллипсоида, гиперболоида; другими словами, радиус шара

Поверхность его будет

Таким образом, искомые поверхности пропорциональны числам

Из только, что приведенной работы проф. И. П. Долбни следует, что отношение поверхностей эллипсоида, параболоида, шара и гиперболоида вращения выражается следующими числовыми данными:

1,7092:1,893:2,2500:3,1855

Действительно, оказывается, что поверхность гиперболоида вращения представляет наибольшую поверхность опоры при определенных линейных размерах. Изучение суставов животных подтверждает, что при движении вокруг одной оси, перекрещивающей ось тела или конечности под прямым углом, суставные поверхности всегда имеют форму поверхности гиперболоида; они поэтому и называются блоковидными суставами. Движения в таких суставах - сгибание и разгибание, при посредстве которых можно, в самом деле, проявлять наибольшую силу, т.е. массовые действия, но менее выгодно приспособляться к препятствиям, которые приходится преодолевать.

При суставах с гиперболическими поверхностями, ось которых пересекает ось тела или конечности под прямым углом, всегда существуют боковые веерообразные связки, волокна которых одними концами сходятся по направлению к концам предполагаемого места расположения оси, а другими расходятся по направлению к боковым частям подвижного отдела конечности. В таких случаях, кроме фиброзной и синовиальной сумок, только такие боковые связки и встречаются.

Если дуги движений в таких суставах не велики и ямка не превышает по своим размерам 90° , то они могут быть простыми, т. е. поверхности ямки и головки будут находиться в тесном соприкосновении между собой. При увеличении ямки толчки и сотрясения сильнее передаются, хрящевая поверхность посередине ямки разъединяется, и появляющиеся вследствие этого бороздки или промежутки выполняются синовией, синовиальными отростками и складками. Примером только что сказанного может служить локтевой сустав человека. У новорожденного и до 14-летнего возраста, когда суставные концы еще в хрящевом состоянии, суставы являются простыми, даже в том случае, если величина ямки доходит до 160° . Как только хрящевые концы соприкасающихся костей окостеневают, хрящ посередине суставной поверхности ямки разъединяется, являются прослойки, и сустав из простого переходит в сложный. Локтевой сустав может, таким образом, служить очень наглядным примером замены тканей одного вида тканями другого вида (в настоящем случае гиалинового хряща синовией, синовиальными ворсинками, складками, отростками) под влиянием измененного питания и механических условий.

С определенной геометрической поверхностью, образованной движением вокруг поперечно расположенной оси, связано определенное расположение мышц; они всегда лежат с вогнутой и выпуклой стороны конечности; равнодействующая существующих здесь мышечных тел пересекает непременно ось движения под прямым углом и прикладывает свои силы к кости, пересекая ту же ось под таким же углом. Мышцы, расположенные около такого сустава, всегда отличаются большой поверхностью своей опоры и большой поверхностью приложения сил, которая всегда удаляется от опоры рычага, над которым действует, приближаясь к его сопротивлению. Мышечных пучков в таких мышцах относительно мало. Так, например, в локтевом суставе человека опора всех действующих сгибателей равна 69,07 см², поверхность приложения сил 7,14 см², а физиологический поперечник 20,3 см². У разгибающих мышц этого сустава опора составляет 63,39 см², поверхность приложения сил 14,03 см², а физиологический поперечник - 31,8 см².

Вместе с определением типа мышц, действующих вокруг сустава с гиперболической поверхностью, определяется также степень развития существующих здесь сосудов. В самом деле, чем больше поверхность опоры и приложения сил, тем относительно меньше количество волокон данной мышцы, а с уменьшением количества волокон уменьшается так же как калибр сосудов, так и толщина их стенок; это видно по исследованиям мышц конечностей верхних и нижних, причем на нижней конечности преобладают мышцы с большой опорой, с большой поверхностью приложения сил и относительно малым поперечником, между тем как мышцы верхней конечности представляют противоположные условия опоры и приложения сил; физиологический же поперечник их относительно велик. Калибр плечевых артерий, по отношению к весу конечности, в 2 или 3 раза превосходит калибр бедренных артерий, по отношению их к весу конечностей (И. Никифоров [3]). При среднем весе верхней конечности 3,594 г общая окружность плечевых артерий равна 24,7, а окружность артерий в процентах к весу верхней конечности 0,7, между тем как при среднем весе нижних конечностей 10482 г общая окружность бедренных артерий - 32,1 мм, а окружность артерий в процентах к весу нижней конечности - 0,31. Относительная толщина стенок плечевых артерий оказывается часто больше толщины стенок бедренных артерий, если сравнить их по весу 1 см² артериальных стенок; в процентах окружности в возрасте от 18 до 35 лет, средним числом, абсолютный вес тех и других артерий может относиться к весу питаемых ими конечностей, как 3,3-1,8. Как сосуды, так и нервы видоизменяются в своем количестве, смотря по типу действующих мышц. Уже Саппей [4] полагал, что количество нервных волокон обратно пропорционально количеству мышечной ткани, в которой они разветвляются. На этом основании, например, такая мышца, как большая ягодичная или как большая приводящая мышца бедра получают тоненькие нервные стволы, между тем как мышцы кисти, лица и в особенности глаз, получают относительно очень толстые стволы. Исследования (И. Войшвилли) [5] показали, что количество нервных волокон мышц глаза относится к мышечным волокнам последних, как 1:14,9 или как 1:18,9, между тем как ветви локтевого нерва относятся к мышцам, в которых они разветвляются, как 1:235,9. В мышцах нижних конечностей эти отношения выступают еще более резко; так, например, большеберцовый нерв дает нервные нити глубоким мышцам на задней поверхности голени в отношении 1:428,8, а мышечные пучки трехглавого разгибателя стопы получают нервные нити в отношении 1:2273. Все эти отношения наглядно показывают ту тесную связь, которая существует между формой суставной поверхности, типом действующих мышц, калибром, ходом и расположением сосудов, питающих эти мышцы, а также калибром, ходом и расположением нервов, идущих к этим мышцам.

Все это относится к простым суставам с гиперболической поверхностью и с движением вокруг одной оси, пересекающей ось тела или конечности под прямым углом. Могут быть, однако же, и сложные суставы с гиперболическими поверхностями; они описываются обыкновенно под названием седлообразных суставов (pedarthrodie). В таких суставах движение бывает всегда вокруг двух осей, лежащих в одной или в двух параллельных плоскостях, пересекающих друг друга под прямым углом. Движение вокруг второй оси в таких случаях возможно вследствие существования прослойки, состоящей из синовии, синовиальных отростков, синовиальных складок, волокнистых, хрящевых, костных и т. п. прослоек. Одно движение в таких случаях происходит между ямкой плюс прослойка с одной стороны и головкой с другой стороны, а другое движение - между головкой плюс прослойка с одной стороны и ямкой с другой стороны. В таких суставах, кроме сгибания и разгибания, существуют еще обыкновенно отведение и приведение, наконец, здесь существуют еще переходные движения в виде круговых движений. Ясно, что такие суставы встречаются в тех местах, где большая сопротивляемость связана с возможностью большим разнообразием движений, как, например, в запястно-перстном суставе большого пальца. От суставов со сферическими поверхностями сложные гиперболические суставы отличаются отсутствием поворота, никогда в них не встречающегося.

Противоположением простым суставам с наибольшей поверхностью опоры в определенном размере могут служить суставы с отрезками цилиндрических или конусообразных поверхностей; это так называемые колесовидные суставы; примером их может служить луче-локтевой сустав. В последнем суставе существуют в верхнем и в нижнем отделах отрезки конусообразных поверхностей. Здесь не могут быть отрезки цилиндрических поверхностей, потому что в таком случае соседние кости в двух частях, расположенных друг над другом, разъединились бы в одной плоскости, чего не может быть; такое разъединение было бы невыгодно относительно крепости соединения; части могли бы скользить друг по другу в вертикальном направлении; все это устраняется при существовании конусообразных отрезков суставных поверхностей, кроме того, на каждой из соседних соприкасающихся костей на одном конце расположена головка, на другом конце той же кости - ямка. В таких случаях разъединение костей не будет в одной плоскости, что и видно в суставе, который приведен как пример: на верхнем конце локтевой кости существует суставная ямка, а на нижнем конце - головка; на лучевой кости - наоборот: на верхнем - головка, на нижнем - ямка; суставные поверхности здесь составляют отрезки конуса, причем на верхней головке поверхности сходятся книзу, а на нижней головке, наоборот, поверхности сходятся кверху, так что конусы, получаемые продолжением этих поверхностей, направляются своими верхушками к середине предплечья. Понятно, что при таких условиях расхождение поверхностей невозможно.

Особенный интерес представляет изучение этих суставов в связи с деятельностью передних конечностей: так, у травоядных одно- и двукопытных, у которых более или менее длинные рычаги поддерживают тело относительно большого размера, разнообразие в движениях уменьшается; остаются только одни сгибания и разгибания, кости предплечья сливаются в виде одной кости (лучевой). У роющих животных, передвигающихся очень быстро и разнообразными способами (плотоядные) и у лазающих животных (обезьяны) наблюдаются всевозможные переходные формы от оболочечного сращения по длине двух костей, прикрытого тонкими, поперечно расположенными мышечными волоконцами, до сустава с верхним и нижним конусообразными отрезками и оболочкой посередине, с поворотом наружу и внутрь при постепенно увеличивающейся дуге движений, которая только у человека доходит до величины 140° и больше. При большой дуге не могут быть большие поверхности соприкосновения, так как чем больше дуга движения, тем больше толчки и сотрясения, связанные с такими движениями. На самом деле оказывается, что при больших дугах движения отрезки поверхности конуса, как видно из математического анализа, являются наименьщей плверхностью соприкосновения при данных линейных размерах.

Суставы с такими поверхностями называются обыкновенно колесовидными (articulationes trochoides); в них возможно движение вокруг одной оси, совпадающей с осью тела или конечности или расположенной параллельно этой оси. Движение вокруг такой вертикальной оси называются поворотами; поворот производится кнаружи (rotatio externa s. supinatio) и внутрь (rotatio interna s. pronatio). Поворот составляет движение, при котором каждая точка движущейся части описывает круг, через центр которого проходит ось движения; при этом движение этой точки по направлению часовой стрелки (при исходном вертикальном положении человека) называется поворотом кнаружи, а обратное движение называется поворотом кнутри.

Поворот есть движение, которое позволяет очень выгодно приспособлять движущуюся часть к препятствию, которое приходится преодолевать; поэтому действия, производимые таким движением, отличаются большой целесообразностью. Если при сгибании можно проявить наибольшую силу, и это движение легче всего производится, то поворотом достигается большая ловкость, т. е. целесообразность и быстрота; так, например, мышцы нижней конечности человека допускают проявление большой силы и продолжительные действия, между тем как мышцы верхних конечностей допускают большее разнообразие в действиях, большую быстроту и относительно малую продолжительность. Поворачивающие мышцы нижних конечностей относятся по своему весу ко всем остальным мышцам этой конечности, как 1: 29,78, между тем как это отношение на верхней конечности 1:4,8, т. е. поворачивающие мышцы на верхних конечностях в 6 раз больше соответственных мышц нижниз конечностей.

Поворачивающие мышцы подходят к кости всегда продольно; они содержат относительно большое число мышечных волокон, относительно богаты сосудами и нервами, чем эти мышцы отличаются от собственно сгибающих мышц, как это сказано выше.

Между животными травоядные отличаются наименьшим разнообразием в своих движениях; у них движения производятся главным образом при посредстве сгибания и разгибания; чем рычаги их конечностей длинее, тем с большей быстротой они передвигаются. Наоборот, плотоядные животные отличаются большим разнообразием в своих действиях; они, как, например, кошачьи животные отличаются пальцевой своей походкой, могут передвигаться очень быстро как по почве, так и по узким перекладинам, по стволам деревьев, могут легко выскакивать из своей засады, ловкими прыжками набрасываться на противника, а своими передними лапами удобно удерживать свою добычу. У них существуют все формы движений, которые они производят с большой ловкостью; эти свойства дают им преимущество перед всеми другими животными и вполне обусловливают все особенности их жизни.

Из всего этого видно, какое большое значение имеет форма движения и как тесно связаны с определенной формой физиологические и психические проявления животного.

2. Суставы с поверхностью, образованной вокруг всевозможных осей,

Поверхность, которая может образоваться движением образовательной вокруг всевозможных осей, проложенных через один общий центр, будет непременно сферической поверхностью; образовательная такой поверхности - полукруг; главные оси можно себе представить проведенными в трех напрвлениях, пересекающих друг друга под прямым углом. Понятно, что в суставах с такими поверхностями движения возможны во все стороны. Величина движений, как и во всех суставах, зависит от разности между ямками и величиной головки. Чем меньше ямка, тем больше дуга движений. Если сравнить эти суставы с суставами с гиперболической поверхностью, то оказывается, что в последних в определенном размере поверхность всегда больше, так как при одинаковых линейных размерах сферическая поверхность относится к поверхности гиперболоида вращения так, как 2,2500:3,1855. В простых суставах с гиперболическими поверхностями ямка составляет обыкновенно около двух третей головки, и движение существует только вокруг одной оси, между тем как в сферических суставах движения самые разнообразные; если дуги движений у них велики, то разнообразие в действиях у них всегда связано с малой крепостью и сопротивляемостью или с относительно малым проявлением сил. Кроме того, так как движения производятся во все стороны, то и опора для движущейся головки должна быть со всех сторон. Наконец, при таких движениях во все стороны толчки и сотрясения также передаются во все сторорны - и тем в большей мере, чем больше дуги движений.

Спрашивается, каким образом получается в таких суставах опора со всех сторон?

Требуется, как уже сказано раньше, чтобы опора была со всех сторон. Допустить существование костной ямки со всех сторон нельзя, так как этим ограничивалась бы величина движения, да и толчки и сотрясения при такой большой поверхности соприкосновения передавались бы очень сильно; следовательно, костная ямка должна быть заменена какой-либо упругой или гибкой тканью; хрящевая или упругая ткань, отдельно взятые, недостаточно крепки для такой опоры, одна плотная соединительная ткань хотя и крепка, но недостаточно упруга: при напоре она легко заходит за пределы упругости, растягивается и весь сустав в таком случае теряет свою сопротивляемость и крепость и получается хлябающий сустав. Остается предположить, что опору составляет свод, состоящий из сухожилий и мышц, который, напрягаясь мышцей будет тем более напряжен, чем более упирается в него головка сустава. Но если бы ямка располагалась с одной стороны, то такие сухожильные своды должны бы были находиться с трех сторон,, что было бы связано с большой тратой материала и сил; остается предположить, что суставная ямка с одним сухожильным сводом будет располагаться по направлению равнодействующей параллелограмма. Действительно, оказывается, что в каждом суставе со сферическими поверхностями существует сухожильный свод, который тем сильнее развит, чем больше сопротивления приходится оказывать головке. Так, например, в плечевом суставе человека суставная ямка оказывает сопротивление снутри и сзади, а сухожильный свод составляет опору спереди и снаружи; свод этот принадлежит сухожилию длинной головки так называемой двуглавой мышцы плеча. Лопатка с ямкой лежат в одной плоскости с сухожильным сводом и именно, как это уже было сказано, по направлению равнодействующей четырех линий, лежащих в наружной, внутренней, передней и задней плоскости. Такие своды встречаются во всех сферических суставах, даже в тех частях, где существуют только отрезки сферической поверхности; у человека такие своды существуют, как уже сказано, в плечевом суставе, в бедренном суставе (длинная головка четырехглавого разгибателя голени), в коленном суставе по задней наружной части (сухожилие подколенной мышцы), в переднем таранном суставе (сухожилие задней большеберцовой мышцы).

При больших дугах движений в суставах, со сферическими поверхностями ямка должна быть тем меньше, чем больше дуга движений, но чем меньше ямка, тем меньше опора, а чем меньше опора, тем меньше сил можно проявить в данном суставе. Для увеличения опоры, причем не уменьшалась бы дуга движения в ямках суставов со сферическими поверхностями, костный край окружен хрящевым краем в виде более или менее резко развитого хрящевого ободка. Такой хрящевой ободок состоит обыкновенно из волокнистого хряща, соединяющего в себе значительную крепость с возможно большей упругостью. Волокна такого хряща идут косо от костного края к свободному краю, обыкновенно в двух направлениях, пересекающих друг друга под прямым углом. Костный край ямки бывает обыкновенно неровный: вырезки по костному краю сменяются выступами, между тем как хрящевой край ровный; поэтому в тех местах, где есть костная вырезка, хрящевой край шире и сидит на узкой ножке, где же костный край представляет выступ, там хрящевой край узок и сидит на широкой ножке. При таком строении и расположении получается упругий, гибкий и крепкий ободок, который оказывает сопротивление при движении и под влиянием давления окружающей среды всегда плотно прилегает к подвижной головке. Пример такого хрящевого края можно встретить в ямке бедренного сустава и плечевого сустава. Сверх того, ямка может еще увеличиваться оболочечным ободком, который может располагаться даже ниже экватора головки. Такой полный ободок существует, например, в виде кругового пояса в бедренном суставе, а в виде неполного ободка — в плечевом суставе (так называемая клювоплечевая связка).

В каждом сферическом суставе прибавочные связки могут являться только в виде косых волокон, являющихся утолщением фиброзной сумки.

Движения в суставах со сферическими поверхностями могут быть во всевозможные стороны. Главные, или основные, движения могут быть: вокруг поперечной оси в виде сгибания и разгибания, вокруг переднезадней, или сагиттальной, оси в виде отведений и приведений, вокруг вертикальной оси в виде поворота кнаружи и внутрь, наконец, могут быть переходные движения от сгибания к отведению, к разгибанию и приведению — это так называемые круговые движения (circumductio).

Раньше уже было сказано о значении сгибания и поворота: при посредстве первого возможно проявление наибольших сил, между тем как при посредстве последнего движения возможно появление большой быстроты вместе с более целесообразным приспособлением к препятствию, которое приходится преодолевать, т. е. возможно проявить наибольшую ловкость в действиях при относительно малом проявлении сил. В суставах со сферическими поверхностями возможно еще, как было сказано только что, отведение и приведение. Отведением называется движение, которое производится вокруг переднезадней, или сагиттальной, оси, причем подвижная часть удаляется от средней линии тела или конечности. При противоположном движении, или приведении, подвижная часть приближается к средней линии тела или конечности. После сгибания наибольшее проявление сил возможно при отведении и приведении, но так как здесь все же обыкновенно принимает участие меньшее число мышечных групп, чем при сгибании, то сравнительно проявление сил меньше. Переходным движением от отведения к разгибанию, далее к приведению и сгибанию будут так называемые круговые движения, при посредстве которых опять же возможно проявить большую ловкость. Действительно, эти движения производятся косыми волокнами, принадлежащими отчасти сгибающим и разгибающим, отчасти отводящим и приводящим мышцам, так что при производстве их участвует относительно малое число мышечных частей, и поэтому проявление сил при посредстве этих движений будет относительно мало.

Приведенные здесь свойства движений имеют большое значение. Ребенок приучается сначала производить только одни сгибания и разгибания, к которым потом присоединяются отведения и приведения, только упражнением приучается человек производить поворот и круговые движения, чтобы затем при их посредстве действовать целесообразно и быстро. Так, например, к самым трудным упражнениям принадлежат поворот и круговые движения спины, поворот в коленном суставе и стопе. Задача физического образования должна заключаться в том, чтобы познакомить ребенка со всеми этими движениями, чтобы при посредстве их увеличить производительность и целесообразность его действий.

Расположение мышц в суставах со сферическими поверхностями выясняется уже указанным отношением их к оси движения. Мышцы эти состоят всегда из пучков косых волокон и содержат большое количество этих волокон. Так называемая перистая мышца, а из сложных мышц раздельно-брюшистая мышца чаще всего встречаются между мышцами, окружающими сустав со сферическими поверхностями.

Относительно сосудов и нервов из всего сказанного следует, что мышцы в сферическом суставе сравнительно всегда богаты сосудами и нервами, вследствие этого допускают действия с различным напряжением и с большими видоизменениями и разнообразием. Все это, однако же, возможно только тогда, когда образованием человек научается владеть и управлять такими двигательными аппаратами, как, например, суставы со сферическими поверхностями.

Полуподвижные суставы. Известно, что величина дуги движения зависит от разности между поверхностями головки и ямки; если они равны между собою, то, понятно, дуга движения равняется нулю. Суставы с такими поверхностями называются полуподвижными суставами; они находятся только в тех местах, где в соседних частях существуют движения по большой дуге, или где толчки, связанные с сотрясением, могут передаваться мозговым центрам, например в запястьях руки, по концам ключицы, в пяточной части стопы и т. д. Геометрическая форма поверхности таких суставов очень разнообразна и находится в зависимости от степени сопротивления в данном суставе. В таких суставах могут быть отрезки гиперболоида вращения, обладающего наибольшей поверхностью при определенных линейных размерах и отличающегося поэтому наибольшей своей сопротивляемостью и крепостью. Примером такого сустава служит пяточно-кубовидный сустав (articulatio calcaneo-cuboidea). Встречаются полуподвижные суставы с отрезками сферических поверхностей, обыкновенно с большим радиусом; у них крепость и сопротивляемость меньше, так как сферические отрезки, как это было доказано выше, представляют меньшую поверхность при определенном линейном размере; таковы пяточно-перстный сустав большого пальца и вообще пяточно-плюсневые суставы II и III пальцев. Наконец, могут быть полуподвижные суставы с отрезками эллиптических, конусообразных или даже цилиндрических поверхностей; с уменьшением их размера уменьшается и сопротивляемость; примером такого сустава может служить таранно-пяточный, или так называемый нижний таранный сустав.

Полуподвижные суставы в простом их виде не допускают никаких движений, так как величины поверхности их ямки и головки равны между собой; они являются только нарушением по протяжению частей опоры; суставные поверхности их прикрыты гиалиновым хрящом с влажной поверхностью, что может служить только для уменьшения толчков и сотрясений, связанных с существующими в соседних частях движениями. При этом оказывается, что в запястных суставах хрящевые поверхности толще, около 2 мм; в соседних частях дуги движений больше (в кистевом суставе дуги движений около 140°); в пяточном суставе хрящевые поверхности тоньше, около 1 мм; в соседних частях дуги движений меньше (в голеностопном суставе дуги движений около 65°). В подвздошно-крестцовом суставе самая тонкая хрящевая поверхность, около 0,4 или 0,5 мм; в соседних частях совершенно не существует движений.

Вследствие отсутствия движений в полуподвижных суставах сумки их всегда коротки; фиброзные сумки содержат обыкновенно прямые волоконца, пересекающие перпендикулярно линию сустава, или же в них существуют накрест идущие волоконца.

Так как движений в полуподвижных суставах нет, то их не окружают мышцы. Если полуподвижные суставы отличаются большой крепостью и сопротивляемостью и поэтому окружены накрест идущими связками, то такие связки всегда находятся под влиянием мышц; соединительная ткань связок — малоупругая ткань; участие мышц присоединяет к крепости связок еще и упругость, поэтому они трудно растягиваются и могут оказывать сопротивление большой тяжести.

Из всего сказанного можно сделать следующие выводы.

1. Лесгафт П. Ф., Долбня И. П. Теория простых суставов. - Известия С.-Петербургской биологической лаборатории. - 1987. - Т. II. - Вып. 2. - С. 22-44.
2. Лесгафт. П. Ф. Основы теоретической анатомии. Ч. I. - СПб., 1892. - С. 158.
3. Никифоров И. Об отношении калибра артерий к весу и объему органов. - СПб., 1883. - С. 42.
4. Traite d'Anatomie descriptive etc., 1876. - C. 26.
5. Материалы к учению об отношении калибра нервов к коже и мышцам человека. - СПб., 1883. - С. 52-53.

Печатается по: Лесгафт П. Ф. Избранные труды по анатомии. - М.: Медицина, 1968. - С. 146-162.

Материалы для публикации подготовлены