физико-математического факультета очного отделения

МАКСИМОВИЧ Ульяны Анатольевны

Научный руководитель:

Кандидат педагогических наук

Профессор кафедры методики

обучения математике и физике

СЕНЬКИНА Гульжан Ержановна

Смоленск

2006

Введение

Глава I.Теоретические основы проблемы математических способностей

Раздел 1 Общая характеристика способностей

1.1.1. Понятие способности

1.1.2. Общие и специальные способности

1.1.3. Способности и задатки

Раздел 2. Математические способности

1.2.1. Исследование математических способностей в зарубежной психологии

1.2.2. Исследование проблемы математических способностей в отечественной психологии

1.2.3. Классификация математических способностей

Глава II. Методика развития математических способностей

Раздел 1. Общая методика

2.1.1. Общие положения теории развития способностей учащихся

2.1.3. Развитие математической одарённости

Раздел 2. Частная методика

2.2.1. Развитие математических способностей на уроках математики

2.2.2. Развитие математических способностей на внеклассных занятиях

Глава III. Разработка базы данных по развитию математических способностей

3.1. Организация данных в базе данных

3.2. Описание работы в базе данных

Заключение

Литература

Приложения

В последнее время во многих странах наблюдается значительный рост интереса к проблемам математического образования. Это связано с тем, что значение математики в жизни человеческого общества возрастает с каждым днём. Высокий уровень развития математики является необходимым условием подъёма и эффективности целого ряда важнейших областей знаний. Как подчёркивают учёные, развитие наук в последнее время характеризуется тенденцией к их математизации, и это касается не только физики, астрономии или химии, но и таких наук, как современная биология, медицина, метеорология, экономика, лингвистика и другие. Математические методы и математический стиль мышления проникают всюду. Трудно найти такую область знаний, к которой математика не имела бы никакого отношения. С каждым годом математика будет находить всё более широкое применение в разнообразных областях человеческой деятельности. Принципиально область применения математики неограниченна, указывает академик А.Н. Колмогоров [9].

В связи с этим в нашей стране ежегодно возрастает потребность в математиках. В последнее время потребность эта явно не удовлетворяется, “математики стали дефицитны”.

Хорошо известно, что основной вклад в развитие той или иной науки делают люди, проявляющие способности в соответствующей области. Всё это выдвигает перед школой задачу всемерного развития у учащихся математических способностей, склонностей и интересов, задачу повышения уровня математической культуры, уровня математического развития школьников. Наряду с этим школа должна уделять особое внимание школьникам, проявляющим высокий уровень способностей к математике, содействовать математическому развитию учащихся, проявляющих особую склонность к изучению математики.

Некоторые считают, что вместо отбора способных к математике школьников необходимо заниматься изысканием возможностей максимального математического развития всех учащихся. Но одно всегда будет дополнять другое, так как и при самых совершенных методах обучения индивидуальные различия в математических способностях всегда будут иметь место – одни и тогда будут более способными, другие – менее способными. Уравнение в этом отношении никогда не будет достигнуто.

Следовательно, учителя математики должны вести систематическую работу по развитию математических способностей у всех школьников, по воспитанию у них интересов и склонностей к математике и наряду с этим должны уделять особое внимание школьникам, проявляющим повышенные способности к математике, организовать специальную работу с ними, направленную на дальнейшее развитие этих способностей.

Несмотря на потребность общества в людях, способных внести свой вклад в развитие математической науки, и возлагающуюся на школу задачу по развитию математических способностей, в современной школе наблюдается следующая ситуация:

• сокращение часов преподавания математики;
• формализм математических знаний;
• отсутствие мотивации учения;
• неумение применять полученные знания на практике;
• отсутствие самостоятельной и творческой деятельности учеников;
• отсутствие в подавляющем большинстве учебников и дидактических пособий заданий, способствующих подготовке учеников к этой творческой деятельности.

Как же помочь учителю в организации учебной деятельности по развитию математических способностей?

Объект исследования моей работы - процесс развития способностей в школе.

Предметом исследования моей работы является процесс развития математических способностей в основной школе.

Целью моего исследования является теоретико-методический анализ проблемы развития математических способностей школьников, и на его основании разработка и описание программного средства, позволяющего наилучшим для учителя образом осуществлять обработку данных по развитию математических способностей.

Гипотеза: программные средства способствуют развитию математических способностей, если

- предлагают систему методических разработок по развитию математических способностей,

- учитывают возраст учеников, типы математических способностей и виды занятий по их развитию,

- ориентированы на снижение временных затрат учителя при подготовке к занятиям,

- обеспечивают актуальность хранящейся информации.

Для осуществления поставленной цели и подтверждения выдвинутых гипотез необходимо выполнить следующие задачи:

• привести литературно-критический обзор по данной проблеме;
• рассмотреть возможности, принципы, особенности методов работы по развитию математических способностей;
• разработать базу данных, которая обеспечивала бы ввод, хранение и автоматизированный поиск информации, необходимой для развития математических способностей;
• провести первичное заполнение базы данных методическими разработками.

Естественно, в своей работе я буду говорить в основном о математических способностях, однако для понимания сложных проблем этой теории следует осветить некоторые фундаментальные вопросы теории способностей.

Прежде всего следует понять, как в психологии трактуют само понятие “способности” и его взаимосвязь с процессом формирования целостной всесторонне развитой личности.

Понятие “способности” употребляется учителем в самых разных сочетаниях: “способный ученик”, “одаренный ученик”, “талантливый ученик”, “у этого ученика есть природные способности”, “у него большие задатки” и т. д. В дидактике и методике преподавания математики мы говорим о творческих, исследовательских, познавательных способностях, о способностях к счёту или другим видам математической деятельности.

Все это многообразие терминологии заставляет задуматься над сущностью понятия.

Российская педагогическая энциклопедия дает следующее определение:

“Способности – индивидуально-психологические особенности личности, являющиеся условиями успешного выполнения определённой деятельности”.

Проблема способностей широко исследовалась и исследуется психологами России.

Одним из основоположников этой теории в нашей стране был Рубинштейн. Он писал: “Под способностями обычно понимают свойства или качества человека, делающие его пригодным к успешному выполнению какого-либо из видов общественно-полезной деятельности, сложившегося в ходе общественно-исторического развития” [20].

Б.М. Теплов [25] включал три признака в понятие “способности”: “Во-первых, под способностями разумеются индивидуально-психологические особенности, отличающие одного человека от другого… Во-вторых, способностями называются не всякие, вообще, индивидуальные особенности, а лишь такие, которые имеют отношение к сущности выполнения какой-либо деятельности или многих деятельностей... В-третьих, понятие “способность” не сводится к тем знаниям, навыкам или умениям, которые уже выработаны у данного человека”. Последнее замечание спорно, так как знания, умения и навыки, которые уже выработаны у учащихся, также требуют от них определенных способностей.

Очень интересно такое заключение Б.М. Теплова: “Не в том дело, что способности проявляются в деятельности, а в том что они создаются в этой деятельности”.

С.Л. Рубинштейн, Б.М. Теплов и многие другие психологи России (А.Г. Ковалев, В.Н. Мяснищев, К.К. Платонов и др.) являются представителями так называемого личностно-деятельного подхода к понятию способностей. Одним из важнейших положений личностно-деятельного подхода является соответствие нервно-психических свойств человека требованиям деятельности. Учебная деятельность сложна и многогранна, она предъявляет определенные требования к психическим и физическим возможностям учащихся. Если особенности учащегося отвечают этим требованиям, то он способен и на высоком уровне осуществлять учебную деятельность. Если такого нет, то у него нет способностей к данной деятельности.

За последние годы сформировался еще один подход к понятию “способности”, который называют функционально-генетическим (В.Д. Шадриков, Е.П. Ильин и др.).

Одной из отличительных черт функционально-генетического подхода к рассмотрению проблемы способностей является признание их генетической обусловленности, врожденности. В.Д. Шадриков [29] определяет способности как “свойства функциональных систем, реализующих отдельные психические функции, которые имеют индивидуальную меру выраженности, проявляющуюся в успешности и качественном своеобразии освоения и реализации отдельных психических функций”.

Широко известно высказывание Б.М. Теплова: “Способности не существуют до деятельности”. В.Д. Шадриков указал на внутреннюю противоречивость этого высказывания: “Если способности не существуют до деятельности, то в деятельности использовать их нельзя, а если способности не только используются в деятельности, но и развиваются в ней, то они существуют до деятельности”.

Следует отметить, что указанные два подхода, по мнению психологов, не противоречат друг другу, а, скорее, их дополняют.

Сложным и не до конца решенным в психологии является вопрос о соотношении общих и специальных способностей.

По диапазону видов деятельности, успех которых обеспечивают те или иные способности, последние подразделяются на общие и специальные.

Крутецкий [12] под общими умственными способностями понимает такие способности, которые необходимы для выполнения не какой-то одной, а многих видов деятельности. К общим умственным способностям автор относит, например, такие качества ума, как умственная активность, критичность, систематичность, быстрота умственной ориентировки, высокий уровень аналитико-синтетической деятельности, сосредоточенное внимание. Специальные способности - это способности, которые необходимы для успешного выполнения какой-нибудь одной определенной деятельности - музыкальной, изобразительной, математической, литературной, конструктивно-технической и т.п.

С.Л. Рубинштейн [19] рассматривал взаимоотношение общей одаренности и специальных способностей: “Специальные способности определяются в отношении к отдельным специальным областям деятельности. Внутри тех или иных способностей проявляется общая одаренность индивида, соотнесенная с более общими условиями ведущих форм человеческой деятельности”.

В этом утверждении есть важная мысль, что общую одаренность надо искать “внутри” специальной одаренности.

Каждый из учебных предметов в школе (физика, история, физкультура и т. д.) требует наряду с более общими способностями некоторых специальных способностей, обусловленных своеобразием этого предмета. Для успешного выполнения каждой деятельности необходимы и более общие и более специальные способности.

В.Г. Ананьев пишет, что “специальные способности связаны как генетически, так и структурно с одаренностью, а одаренность конкретно проявляется в специальных способностях и развивается в них. Это очевидное положение приходится подчеркивать, так как за последнее время в психологической литературе проявляется тенденция свести всю проблему к изучению специальных способностей, фактически игнорируя явление общей одаренности”.

В.А. Крутецкий [12] так говорит о специальных способностях: “Задача всестороннего развития способностей, как нам кажется, должна дополняться не менее важной задачей выявления тех детей, которые обнаруживают особые склонности и способности к отдельным видам деятельности (математике, технике, литературе и т. д.) и предоставления им возможностей для дальнейшего развития в этом направлении. Иначе говоря необходимо ориентироваться на такой подход в обучении, который, реализуя всестороннее развитие способностей каждого, одновременно максимально содействует росту способностей к тем видам деятельности в обучении, в которых ученик показывает наибольшие успехи и удовлетворяет наибольший интерес”.

В исследовании проблемы способностей есть один очень сложный, интересный и загадочный вопрос: каково происхождение способностей? Психологи ведут по этому поводу многолетние дискуссии. Они связаны с понятием задатков. По поводу задатков можно прочитать многое. Вслед за Б.М. Тепловым [25] следует считать, что задатки, талант — это врожденные качества, и их наличие означает, что при прочих равных условиях они значительно облегчают формирование способностей, помогают раньше их выявить и успешно развивать; на базе различных по структуре задатков могут сформироваться сходные способности и, наоборот, на базе сходных задатков — разные способности и т. д. С.Л. Рубинштейн [19] писал: “Во всех случаях мы разумеем “врожденность” не самих способностей, а лежащих в основе их развития задатков”.

Психолог Л.А. Венгер [2] ставит эти идеи под сомнение: “Дети рождаются не одинаковыми. Уже в первые недели их жизни обнаруживаются различия в их возбудимости, активности, в быстроте и устойчивости реакций на внешние воздействия. У младенцев наблюдается разный темп развития движения, неодинаковое воздействие оказывают на них одни и те же внешние впечатления. Беда, однако, заключается в том, что еще никому не удавалось установить связь между индивидуальными особенностями младенцев и последующим развитием их способностей. Предположение о задатках — пока что простое умозаключение, вытекающее из того, что в ходе обучения и развития способностей заметна разница между детьми и что у некоторых детей легче формируются, например, математические, у других — литературные способности”. В конце Л.А. Венгер пишет: “Окончательное разрешение спора о задатках принадлежит будущему. Пока ясно одно: способности, достаточные для усвоения всех предметов школьной программы, плодотворного творческого труда в самых различных (если и не во всех) областях производства, науки, искусства, могут быть сформированы у любого здорового ребенка”. Вот почему можно утверждать, что определенный уровень математических способностей присущ каждому школьнику. Необходимо только понимать, что эти уровни существуют, уметь их выявлять и развивать.

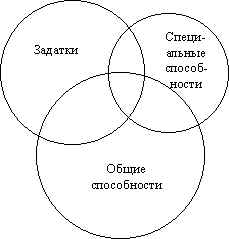
Руководствуясь соображениями здравого смысла, соотношение способностей человека может быть представлено диаграммой, которая напоминает круги Эйлера. Здесь очень важно пересечение всех трех кругов — именно оно определяет основные личностные качества человека, уровень его сформированности. Естественно, сколько людей, столько и возможных пересечений как всех кругов, так и каждой пары. Заметим, что радиусы кругов, естественно, различны и могут в какой-то степени иллюстрировать наличие тех или иных способностей (если научиться их измерять).

В исследование математических способностей внесли свой вклад такие яркие представители определенных направлений в психологии, как А.Бинэ, Э.Трондайк и  Г. Ревеш, и такие выдающиеся математики, как А.Пуанкаре и Ж. Адамар.

Большое разнообразие направлений определило и большое разнообразие в подходе к исследованию математических способностей, в методических средствах и теоретических обобщениях.

Единственное, в чем сходятся все исследователи, это, пожалуй, мнение о том, что следует различать обычные “школьные” способности к усвоению математических знаний, к их репродуцированию и самостоятельному применению и творческие математические способности, связанные с самостоятельным созданием оригинального и имеющего общественную ценность продукта.

Большое единство взглядов проявляют зарубежные исследователи по вопросу о  врожденности или приобретенности математических способностей. Если и здесь различать два разных аспекта этих способностей – “школьные” и творческие способности, то в отношении вторых существует полное единство – творческие способности ученого-математика являются врожденным образованием, благоприятная среда необходима только для их проявления и развития. В отношении “школьных” (учебных) способностей зарубежные психологи высказываются не столь единодушно. Здесь, пожалуй, доминирует теория параллельного действия двух факторов – биологического потенциала и среды.

Основным вопросом в исследовании математических способностей (как учебных, так и творческих) за рубежом был и остается вопрос о сущности этого сложного психологического образования. В этом плане можно выделить три важные проблемы.

1.      Проблема специфичности математических способностей. Существуют ли собственно математические способности как специфическое образование, отличное от категории общего интеллекта? Или математические способности есть качественная специализация общих психических процессов и свойств личности, то есть общие интеллектуальные способности, развитые применительно к математической деятельности? Иначе говоря, можно ли утверждать, что математическая одаренность – это не что иное, как общий интеллект плюс интерес к математике и склонность заниматься ею?

2.      Проблема структурности математических способностей. Является ли математическая одаренность унитарным (единым неразложимым) или интегральным (сложным) свойством? В последнем случае можно ставить вопрос о структуре математических способностей, о компонентах этого сложного психического образования.

3.      Проблема типологических различий в математических способностях. Существуют ли различные типы математической одаренности или при одной и той же основе имеют место различия только в интересах и склонностях к тем или иным разделам математики?

По вопросу о специфике математических способностей, хотя и нельзя констатировать наличие единого мнения, но большинство ученых, среди которых такие крупные авторитеты в области психологии, как А. Бинэ, Г. Ревеш, и в области математики, как Ж. Адамар и А. Пуанкаре, явно склоняются в пользу признания специфичности математического таланта. А. Бинэ прямо и недвусмысленно указывал на то, что “математический ум предполагает совершенно специальную способность”. А. Пуанкаре и впоследствии Ж. Адамар говорили о специфике мышления математика, о своеобразной, свойственной математикам “математической интуиции”, о подсознательной творческой работе. Хотя Адамар и отмечал, что математическая одаренность и математическое творчество как-то связаны с общим интеллектом, творчеством вообще (упоминая в этом отношении о фактах связи математической одаренности с одаренностью в других областях), но он же указывал на частые случаи “ограниченности” математического ума. Ревеш высказывает убеждение в том, что математический талант есть специфическая форма таланта, которую необходимо отличать от других форм научного таланта. Математический талант может проявляться вместе с другими талантами, но он органически не связан с ними; таланты к другим наукам возможны без математической способности и даже при абсолютном отсутствии последней.

Вопрос о структурности математических учебных способностей принимал у психологов прежде всего форму вопроса о том, нужно ли говорить о математических способностях как об едином свойстве или правильнее говорить об арифметических, алгебраических и геометрических способностях. Еще в 1909—1910 гг. К. Стоун и независимо от него С. Куртис, изучая достижения в арифметике и способности к этому предмету, пришли к выводу о том, что едва ли можно говорить о математических способностях как об едином целом, даже в отношении арифметики. В 1910 г. была опубликована большая статья В. Брауна “Объективное исследование математических способностей”, в которой говорилось, что успешность в алгебре и геометрии определяется качественно различными свойствами и что нет свойства, которое лежало бы в основе математических способностей вообще. Исследований по выявлению компонент математических способностей проводилось большое количество, но они не дают более или менее ясного и четкого представления о структуре математических способностей. Для примера приведу результаты исследования структуры математического мышления, проводимого В. Хаекером и Т. Цигеном. Авторы прежде всего выделили четыре основных сложных компонента, составляющие “ядро” математического мышления: пространственный, логический, числовой и символический. Дальше они попытались каждый из этих компонентов разложить на более простые составляющие. Получилась такая схема:

A. Пространственный компонент.

1. Понимание пространственных фигур, образов и их комплексов (синтезов, гештальтов).
2. Память на пространственные образы (пространственные
   представления).
3. Пространственные абстракции (умение видеть у пространственных объектов общие признаки).
4. Пространственное комбинирование (понимание и самостоятельное нахождение связей и отношений пространственных объектов).

B. Логический компонент.

1. Образование понятий (типа “синус”, “логарифм”, “тензор”
   и т. д.) и понятийных абстракций.
2. Понимание, запоминание и самостоятельное нахождение
   общих понятийных связей.
3. Понимание, запоминание и самостоятельное выведение
   заключений и доказательств по правилам формальной
   логики.

C. Числовой компонент.

1. Образование числовых представлений.
2. Память на числа, числовые решения.

D. Символический компонент.

1. Понимание символов.
2. Запоминание символов.
3. Операции с символами.

Обобщая результаты большинства исследований, мы получим самые общие характеристики математического мышления, такие, как способность к абстракции, способность к логическому рассуждению, хорошая память, способность к пространственным представлениям и т. д.

Перейдём к вопросу о типологии математических способностей. Наиболее распространенной в зарубежной психологии является типология математических талантов, основанная на противопоставлении дискурсивного, развернутого во всех своих звеньях мыслительного процесса, интуитивному мыслительному процессу, связанному с непосредственным “схватыванием” необходимых отношений. Еще Р. Декарт в своих “Правилах для руководства ума” противопоставлял цепи последовательных логических умозаключений интуицию как непосредственное усмотрение связей и отношений между различными явлениями. Ж. Адамар говорит о логическом и интуитивном математическом мышлении (и соответственно о двух типах математиков). “Логика” отличает значительно меньший “удельный вес” бессознательного в мышлении, более узко направленная мысль, последовательность и ясная расчлененность мыслительного процесса. Мышление “интуитивиста” характеризуется значительно большим удельным весом бессознательного, более “рассеянной” мыслью, быстротой и сокращённостью (“свернутостью”) мыслительного процесса.

Интересен взгляд западных учёных на сущность математического творчества. В работах А. Пуанкаре, Ж. Адамара, Г. Ревеша встречаются следующие идеи. Ход мыслительного процесса ученого может осознаваться не во всех своих звеньях. Ученому свойственно не только “развернутое” дискурсивное мышление, но и так называемое интуитивное мышление, протекающее в сокращенном, “свернутом” виде. Оно усматривает или открывает существенные связи раньше, чем дискурсивное мышление успеет доказать их соответствие действительности. Это часто и воспринимается как бессознательная творческая работа. Можно установить определенные стадии творческого процесса: 1) период бесплодного сознательного обдумывания; 2) период отвлечения от работы, период отдыха или переключения на другую деятельность. В это время активно работает подсознательное мышление, происходит “инкубация” идеи; 3) внезапное “озарение”, открытие истины в тот момент, когда человек меньше всего думает о предмете; 4) снова сознательная работа над анализом и отшлифовкой идеи.

Свои взгляды на природу и сущность математических способностей или математического мышления высказывали многие математики и методисты.

Одним из первых отечественных авторов, затрагивающих проблему математических способностей, был русский математик Д.Д. Мордухай-Болтовский. Основные мысли о математическом творчестве он изложил в оригинальной статье “Психология математического мышления”. Автор предлагает следующий перечень компонентов, в совокупности образующих математические способности: “Хорошая математическая способность предполагает сильную память и причем главным образом на предмет того типа, с которым имеет дело математика”; “остроумие”, т. е. способность “обнимать умом зараз два совершенно разнородных предмета”; “быстрота мысли”, которую автор связал с “бессознательным мышлением”. Д.Д. Мордухай-Болтовский отметил различие двух типов воображения: абстрактного у “алгебраистов” и более конкретного у “геометров”.

А.Я. Хинчин [26] указывал следующие черты математического мышления: 1) доминирование логической схемы рассуждений, 2) лаконизм (стремление находить кратчайший путь к цели), 3) четкое расчленение хода рассуждений, 4) точность (каждый математический символ имеет строго
определенное значение).

А.Н. Колмогоров в работе “О профессии математика” указывал, что способности к механическому запоминанию большого числа фактов, формул, складывание и перемножение в уме длинных рядов многозначных чисел не имеют отношения к математическим способностям. Он отмечал, что различные стороны математических способностей встречаются в разных комбинациях, что эти способности проявляются обычно рано и требуют непрерывного упражнения. К математическим способностям А.Н. Колмогоров относил: 1) способность умелого преобразования буквенных выражений, нахождения удачных путей для решений уравнений, не подходящих под стандартные правила, или, как принято называть у математиков, “вычислительные или алгоритмические способности”; 2) геометрическое воображение или “геометрическую интуицию”; 3) искусство последовательного правильно расчлененного логического рассуждения.

Б.В. Гнеденко [6] выделяет следующие свойства математического мышления: 1) способность улавливать нечеткость рассуждения, отсутствие необходимых звеньев доказательства; 2) привычку к полноценной логической аргументации; 3) четкую расчлененность хода рассуждений; 4) лаконизм; 5) точность символики.

С.И. Шварцбурд считал, что главным элементом математического воспитания следует признать воспитание творческой деятельности учащихся, и выделял компоненты “математического развития”, которые рассматриваются в методической литературе: развитие пространственного представления; умение отделить существенное от несущественного; умение абстрагировать; умение абстрактно мыслить; умение от конкретной ситуации перейти к математической формулировке вопроса, к схеме, сжато характеризующей существо дела; обладание навыками дедуктивного мышления; умение анализировать, разбирать частные случаи; применение научных выводов на конкретном материале; умение критиковать и ставить новые вопросы; владение достаточно развитой математической речью, как письменной, так и устной; обладание достаточным терпением при решении математических задач.

Самое значительное исследование психологов по данной проблеме принадлежит В.А. Крутецкому и изложено в его книге “Психология математических способностей школьников”. В. А. Крутецкий даёт следующее определение математическим способностям: "Под способностями к изучению математики мы понимаем индивидуально-психологические особенности (прежде всего особенности умственной деятельности), отвечающие требованиям учебной математической деятельности и обусловливающие на прочих равных условиях успешность творческого овладения математикой как учебным предметом, в частности относительно быстрое, легкое и глубокое овладение знаниями, умениями и навыками в области математики". Собранный В. А. Крутецким материал позволил ему выстроить следующую общую схему структуры математических способностей  в школьном возрасте.

1)  Способность к формализованному восприятию математического материала, схватыванию формальной структуры задачи.

1)  Способность к логическому мышлению в сфере количественных и пространственных отношений, числовой и знаковой символики. Способность мыслить математическими символами.

2)  Способность к быстрому и широкому обобщению математических объектов, отношений и действий.

3)  Способность к свертыванию процесса математического рассуждения и системы соответствующих действий. Способность мыслить свернутыми структурами.

4)  Гибкость мыслительных процессов в математической деятельности.

5)  Стремление к ясности, простоте, экономности и рациональности решений.

6)  Способность к быстрой и свободной перестройке направленности мыслительного процесса, переключению с прямого на обратный ход мысли (обратимость мыслительного процесса при математическом рассуждении).

1)  Математическая память (обобщенная память на математические отношения, типовые характеристики, схемы рассуждений и доказательств, методы решения задач и принципы подхода к ним).

1)  Математическая направленность ума.

Выделенные компоненты тесно связаны, влияют друг на друга и образуют в своей совокупности единую систему, целостную структуру, своеобразный синдром математической одаренности, математический склад ума.

Не входят в структуру математической одаренности те компоненты, наличие которых в этой системе не обязательно (хотя и полезно). В этом смысле они являются нейтральными по отношению к математической одаренности. Однако их наличие или отсутствие в структуре (точнее, степень их развития) определяют тип математического склада ума. Не являются обязательными в структуре математической одаренности следующие компоненты:

1.  Быстрота мыслительных процессов как временная характеристика.

2.  Вычислительные способности (способности к быстрым и точным вычислениям, часто в уме).

3.  Память на цифры, числа, формулы.

4.  Способность к пространственным представлениям.

5.  Способность наглядно представить абстрактные математические отношения и зависимости.

Исходя из всего вышесказанного и основываясь на компонентах (параметрах) математических способностей, выявленных математиками, педагогами и психологами в нашей стране и за рубежом, проведу систематизацию этих параметров предложенную В.А. Гусевым в его работе “Психолого-педагогические основы обучения математике”.

Классифицируя составляющие математических способностей, автор пришёл к выводу, что прежде всего их можно распределить по двум основным блокам: в первый блок входят общие характеристики мышления или умственной деятельности (формулировки этих качеств личности формально не связаны ни с какой специальной математической деятельностью); ко второму блоку относятся параметры математических способностей, непосредственно связанные с математической деятельностью учащихся. Совершенно ясно, что эти параметры следует идентифицировать по уровню их сложности, продвинутости и т. д. Отмечу при этом, что все составляющие взяты автором из соответствующих исследований, выполненных к настоящему времени.

Итак, рассмотрим один из возможных вариантов классификации составляющих (параметров) математических способностей учащихся (см. Приложение 1).

Оценивая предложенную классификацию параметров математических способностей, можно сделать следующие выводы.

1. Отличительной чертой данной классификации является ее направленность на целостное формирование личности каждого школьника, и в этой связи ее многогранность.
2. Бросается в глаза большое пересечение указанных параметров с общими целями обучения математике, сложность этих взаимосвязей. Важно отметить, что фундаментом во всем этом многообразии являются мыслительные процессы, это выдвигает на первый план процессы формирования приемов мыслительной деятельности.
3. Построенная классификация играет немаловажную роль
   в диагностике параметров математических способностей учащихся и позволяет дифференцировать их по уровням владения теми или иными приемами мыслительной деятельности.
4. Особенно важно, что здесь выделяются некоторые врожденные параметры (задатки), о которых нам известно немногое.

Под математическими способностями следует понимать специальные особые способности, которые необходимы для успешного выполнения математической деятельности. Математические способности являются не единым образованием, а имеют сложную многогранную структуру. Успешность математической деятельности зависит не от отдельно взятой способности, а от комплекса способностей. Математическая одарённость предполагает наличие определённых природных предпосылок и проявляется только в творческой деятельности. Однако не следует забывать, что каждый человек (ученик) обладает в определенной мере математическими способностями. Оценить и развить эти способности — задача педагогов.

Диалектико-материалистическая концепция развития способностей, преобладающая в отечественной психологии, опирается на следующие положения. Все психические явления, включая способности, являются вторичными образованиям по отношению к объективному миру, образу жизнедеятельности человека, его обучению и воспитанию, которые служат причиной, источником психического развития. Анатомо-физиологические задатки выступают лишь необходимые условия развития человека и его способностей. Способности имеют общественно-исторический характер. Их разнообразие порождено большим количеством исторически сложившихся видов деятельности, профессий, специальностей. Способности в своем развитии в основном определяются образом жизни и деятельности и изменяются с изменением жизнедеятельности. В формировании и развитии способностей решающую, определяющую роль играют внешние условия, обучение и воспитание в самом широком смысле слова, те виды деятельности, которые выполняет человек. Личность формирует и развивает свои способности в процессе усвоения и приумножения опыта прошлых поколений, воплощенного в продуктах материальной и духовной культуры. Формирование и развитие способностей определяется не только достигнутым уровнем культурного развития страны, наличием продуктов культуры, в которых воплотились способности человека, а прежде всего эффективностью способов усвоения (присвоения), созидания и усовершенствования этих продуктов в процессе рационально организованной деятельности. Причем не всякая деятельность развивает и формирует способности человека. Рассматривая общую структуру жизнедеятельности человека, нетрудно заметить существование видов деятельности, не развивающих, а наоборот, отвлекающих и даже тормозящих развитие его основных способностей. Так, если человек, имеющий музыкальные или изобразительные наклонности задатки, вынужден заниматься тяжелым физическим трудом, то эта деятельность вряд ли будет развивать его потенциальные способности к музыке и живописи. Когда говорят о развивающей деятельности применительно к отдельному индивиду, то имеют в виду, что она, во-первых, выступает как значимая для него, как деятельность, вокруг которой аккумулируются и реализуются все возможности человека. Поэтому, чтобы понять, является ли данная деятельность развивающей, ей необходимо дать личностную характеристику. В этом смысле даже профессиональная деятельность, проходящая через всю жизнь человека, не всегда может быть значимой для индивида. Главным признаком значимости деятельности является то, что он идет на свою работу как на праздник, с большим воодушевлением. Во-вторых, такая деятельность должна быть организована в соответствии со следующими принципами: носит не репродуктивный, а творческий (во всяком случае субъективно-творческий) характер; отвечает принципам развивающего обучения, которое ведется на повышенном уровне сложности и опережает развитие, ведя его за собой, ориентируясь на те компоненты способностей, которые еще не полностью сформировались и которые формируются под влиянием такого обучения; деятельность положительно мотивирована: учащиеся испытывают чувство большой радости, совершая ее, и отчетливо понимают свои недостатки и допускаемые ошибки, видят результаты своих действий, осознают и объективно оценивают свое продвижение к цели на каждом этапе деятельности, заметно переживают успехи и относительные неудачи.

Задача разностороннего развития способностей должна дополняться не менее важной задачей выявления одаренных детей и предоставления им возможностей для дальнейшего развития. Иначе говоря, необходимо ориентироваться на такой подход в обучении, который, реализуя разностороннее развитие способностей каждого, одновременно максимально содействует росту способностей к тем видам деятельности, к которым ученик проявляет наибольший интерес и может достичь наибольших успехов.

Для реализации данной концепции развития способностей необходимо: а) создать в учебных заведениях и внешкольных учреждениях условия, благоприятствующие формированию и развитию способностей учащихся; б) применить эффективные формы учебно-воспитательной работы; в) применить рациональные методы и приемы диагностики и развития способностей.

Как известно из психологии и педагогики, благоприятными условиями для воспитания способностей являются:

• любовь к детям и педагогической деятельности, глубокое знание индивидуально-психологических и возрастных особенностей учащихся, хорошее знание своего дела (содержания, форм и методов учебно-воспитательной работы);
• признание в учебном заведении в системе ценностей приоритета творческой деятельности и творческой личности; творческий климат в учебном заведении и внешкольном учреждении;
• соблюдение в процессе управления учебно-творческой деятельностью учащихся гуманного, демократического стиля общения;
• проблемное обучение; решение творческих задач; показ значимости организуемой творческой деятельности для воспитания способностей;
• сотрудничество (сотворчество) педагога и учащихся (осуществление совместных поисков условий и средств для развития творческих способностей); сам педагог как образец творческой личности с ярко выраженной установкой на педагогическое творчество;
• уважение к личности учащегося в сочетании с разумной требовательностью (анализ типичных ошибок и недостатков - только в доброжелательной форме);
• организация самостоятельной деятельности (все то, что учащиеся могут выполнить без помощи педагога, они должны выполнить самостоятельно);
• индивидуальный подход к учащимся в процессе выявления и развития способностей;
• применение педагогом методов поощрения учащихся; выражение оптимизма и веры в творческие возможности учащихся;
• хорошая обеспеченность педагога научно-методической литературой и техническими средствами обучения;
• высокий уровень внеклассной работы;
• система морального и материального поощрения творчески работающих педагогов; внедрение в практику работы учебного заведения передового педагогического опыта;
• наличие дифференцированного обучения и т.д.

Для воспитания способностей большое значение имеют следующие формы учебно-воспитательной работы: кружки, диспуты, семинары, конференции, КВН, экскурсии, творческие уроки, факультативы, индивидуальное обучение, индивидуальный подход к учащимся, дифференциация обучения, коллективные формы обучения, исследовательская и опытническая работа, викторины, игры. конкурсы, клубы по интересам, кино-, изо- и фотостудии, научно-технические общества, фестивали, смотры, вечера вопросов и ответов, конкурсы, турниры, олимпиады, лекции, беседы, выставки, практикумы, дополнительные индивидуальные занятия с учащимися, домашняя работа учащихся и др.

Основные направления в развитии и формировании способностей предусматривают следующие мероприятия. Во-первых, выявление (диагностика) природных задатков к определенной деятельности и анализ качества результатов деятельности. Во-вторых, тренировка и развитие природных свойств личности путем ее включения в систематическую деятельное под руководством специалиста (учителя).

В данном разделе описываются наиболее существенные принципы работы по развитию математических способностей учащихся, реализуемые как на уроках, так и на внеклассных занятиях. Принципы составлены Э. Ж. Гингулисом [5] на основе анализа опыта работы по развитию математических способностей учащихся.

Принцип активной самостоятельной деятельности учащихся. Он требует от учителя четкого выделения времени на объяснение нового материала. Предпочтительно вводить теоретический материал довольно крупными порциями — тем самым быстро осознается достаточно полная система фактов, необходимых для решения задач по данной теме. Но после этого нужно отвести не часть урока, а одно или несколько занятий полностью на решение задач. Обычно ребятам сообщают номера (или тексты) сразу всех 5—6 задач, которые будут решены на уроке или на кружке. Класс работает самостоятельно. Сильные учащиеся при этом загружены весь урок, хотя оформлять решение до конца для них необязательно, достаточно сообщить учителю о том, что получены верные ответы. Основная часть класса справляется с меньшим числом заданий, но при этом тоже работает самостоятельно. Роль учителя сводится к выборочному контролю, к занятию с отстающими.

Принцип учета индивидуальных и возрастных особенностей учащихся предполагает наличие у учителя четких представлений о возможностях каждого ученика, о динамике роста его потенциала. С учетом этой динамики нужно предлагать индивидуальные задачи. Они должны быть доступными для учащихся средних возможностей. Тем самым ребята предохраняются от обескураживающего действия неудачи. В то же время более способные ребята требуют трудных задач, на которых они могут испытать свои умственные силы. Подготовка индивидуальных заданий требует от учителя широкой “задачной эрудиции”.

К методическим средствам реализации указанного принципа относятся краткие содержательные обсуждения идей и методов решения.
На определенном этапе — на рубеже VII—VIII классов — учащиеся начинают понимать, что усвоение нового метода способствует успеху в большей мере, нежели доведенное до конца “кустарное” решение.

Принцип постоянного внимания к развитию различных компонентов математических способностей заставляет отметить сложность проявления этих способностей. Учителя почти никогда не знают, какой подход обеспечит данному ученику наибольший успех и продвижение
вперед. Кажется логичным заключить, что наибольшие достижения возможны при достаточном внимании ко всем компонентам математических способностей.

Достигается это с помощью правильного подбора тематики задач, рассмотрения различных подходов к решению одной и той же задачи. Полезны приемы, направленные на повышение удельного веса геометрических, наглядных соображений. Они экономят время урока, так как наглядность может заменить и словесную формулировку условия, и подробную запись решения.

При разборе задач очень важно помнить о принципе соревнования. Во внеурочных условиях хорошо зарекомендовали себя различные математические олимпиады, “бои” и т. д., но элементы состязания возможны и на уроке. К соревнованию побуждают следующие вопросы учителя: “Кто решит быстрее? У кого решение получилось самое короткое? Самое простое? Самое неожиданное?” и т. д.

Иногда высказывается мнение, что соревнования травмируют, деформируют сознание школьников и в результате слабые учащиеся еще острее чувствуют свою отсталость, а лучшие “математики” класса зазнаются. Эти опасения имеют основания. Но существуют и меры компенсации: предлагаемые задания должны быть посильны. Следует учитывать также, что учащиеся VII — IX классов уже довольно трезво оценивают свои математические способности. Венгерский психолог Э. Гефферт установила, что высокоодаренность не сочетается с эгоцентризмом и негативными социальными установками. Э. Гефферт пришла также к следующему выводу: “С радостью выполненная деятельность оплачивает сама себя, причем не ожидается дополнительного признания”.

Рассматривая задачи, доступные учащимся, нельзя забывать о принципе профессионализма. Он требует, чтобы школьники уверенно владели системой опорных задач. Для этого нужна ежедневная работа по закреплению навыков, повторению ключевых идей и методов. Кроме того необходимо следовать принципу яркости. Это означает, что занятия должны быть разнообразны по форме и интересны по содержанию. Свою подлинную увлеченность предметом учитель может продемонстрировать подбором красивых и разнообразных задач, рассказами из истории математики.

На внеурочных занятиях есть возможность реализовать принцип полной нагрузки. Речь идёт о поддержании достаточно высокого уровня задач, предлагаемых на кружке или факультативе. Кроме того, имеется в виду повышенная скорость обсуждения решений и большая нагрузка на домашнюю работу ученика. Дома школьник в состоянии подготовить доклад по какому-то теоретическому вопросу, придумать красивую задачу, написать сочинение на математическую тему и т. д.

B заключение подчеркнем, что развитие у учащихся математических способностей напрямую зависит от личности учителя. Если школьникам
будет неинтересно с ним, если они не почувствуют роста своих возможностей, то они прекратят углубленные занятия математикой.

2.1.3. Развитие математической одарённости

Для освещения проблемы одарённости в своей работе за основу я взяла жизненный путь и взгляды замечательного русского математика –Колмогорова Андрея Николаевича. Такой выбор неслучаен, так как в случае А.Н. Колмогорова нам предлагается редкая и, видимо, полезная в научном смысле ситуация: – математический гений размышляет по поводу развития математических способностей у детей и юношества. Следует учесть при этом, что он почти всю жизнь конкретно, как педагог, занимался развитием одаренных детей и юношей, постоянно анализируя свой собственный опыт в этом отношении.

На вопрос о пути своего становления как математика Андрей Николаевич отвечал, что его путь в математику был “извилистым”. В детстве Колмогоров не был вундеркиндом. Иначе говоря, не было того резкого умственного опережения, которое заставляет окружающих возлагать на ребенка особые, редко оправдывающиеся надежды на замечательное будущее. Правда, как он сам пишет [9], “интерес к математике проявился достаточно рано. Так, где-то в четыре-пять лет придумал и сам решил такую задачу: имеется пуговица с четырьмя дырочками. Для ее закрепления достаточно протянуть нитку, по крайней мере, через две дырочки. Сколькими способами можно закрепить пуговицу?”.

В этом же возрасте, по его словам, “испытал радость математического открытия”, открыв закономерность - образование последовательных квадратов:

1=1²
1+3=2² 

1+3+5=3²
1+3+5+7=4² и так далее.

Но потом, в средних классах, победили другие интересы: он всерьез увлекается биологией, потом появились шахматы. Когда кончил среднюю школу, то занимался серьезным образом в семинаре С.В. Бахрушина. При этом увлекала металлургия и параллельно с университетом поступил на металлургический факультет химико-технологического института и некоторое время там проучился. “Окончательный выбор математики как профессии,- пишет Колмогоров, - произошел, когда я начал получать первые самостоятельные научные результаты, то есть лет с восемнадцати-девятнадцати”.

Свой обычный, ни в коей мере не ускоренный тип развития Колмогоров рассматривал как неслучайный и принципиальный для развития творческих способностей и несколько скептически относился к так называемым “вундеркиндам”.

А.Н. Колмогоров уже тогда, тридцать лет назад, видел опасность, которая сейчас стала очевидной для большинства психологов, работающих в области одаренности. Он весьма скептически относился к тому, что по выражению Н.С. Лейтеса, относится только к “возрастной одаренности”. Колмогоров в переписке с Крутецким пишет, что “мы теряем много медленно развивающихся потенциально крупных талантов” [29]. И далее еще жестче - “ в последние годы эта опасность сильно возросла при развившемся ажиотаже вокруг “одаренности” и особенно математической”.  Ускоренное прохождение школьной программы, вообще ускоренное развитие, которое много лет является чуть ли не главным критерием высоких способностей, по мнению Колмогорова, мало о чем свидетельствует. 

Именно потому для всех, кто работает с одаренными детьми- математиками, он ставит следующие вопросы:

1. “в каком возрасте можно, независимо от тренированности и различий в физиологически обусловленных темпах развития уловить хотя бы в первом приближении математические способности…

2. в каком возрасте форсированное развитие задатков математического мышления уже реально влияет на достижение “потолка” способностей”.

Оба этих вопроса в другом месте – в ответах на анкету - формулируются им с почти максимальной степенью четкости:
“сейчас дело идет о выявлении математически одаренных детей с целью организованного форсирования их математических занятий. Следует решить не вопрос о том, когда это возможно, а когда это целесообразно (подчеркнуто А.Н. Колмогоровым)”.

Такую постановку вопроса он дополняет личным опытом, весьма уместным, имея в виду масштаб его математического дарования: “ что касается лично меня, то я думаю, что ни я сам, ни математическая наука ничего не потеряли из–за того, что задача “выявления” (кавычки Колмогорова) моих математических способностей была предоставлена мне самому. Я начал систематически дополнительно заниматься математикой в возрасте 15-16 лет, когда сам решил, что это серьезное и нужное дело”.

Есть и другая точка зрения, которой следуют многие наши педагоги и даже психологи - специалисты по одаренности. Они считают, что чем раньше развивать специальные способности, тем лучше. (Кстати, и В.А. Крутецкий, в переписке с которым Андрей Николаевич обозначил эти мысли, судя по монографии, считал возможным и необходимым ранние специализированные занятия с одаренными к математике детьми.) Если иметь в виду последние физиологические и психофизиологические исследования о сензитивных периодах развития, с одной стороны, и исследования о закономерностях развития общих способностей, с другой, то приходится признать, что позиция, представленная выдающимся математиком, психологически значительно больше обоснована, чем бытующая в ряде школ система раннего интенсивного и специализированного обучения одаренных детей.

Как считает Колмогоров, “до 10-12 лет - с довольно хорошим успехом заменим общим воспитанием сообразительности и умственной активности”. “ Весьма желательны”, - пишет Колмогоров,- и внешкольные занятия - типа математических кружков, но в них “ следует по возможности избегать установки на предопределение будущих профессиональных интересов” [9].

Другое дело старшие классы, где “запоздание с усвоением строгой логики и специальных математических навыков в 14-15 лет делается уже трудно восполнимым”.

Уже тогда, тридцать лет назад, Колмогоров четко определяет для себя разницу между высокими способностями к изучению математики, с одной стороны, и собственно творческими способностями в этой области, с другой.

По мысли Колмогорова, чтобы стать творческим математиком, нужно, во-первых, сохранять, культивировать у себя своего рода “детское мышление”. По мнению А.Н. Колмогорова, способности к математическому творчеству у человека тем выше, чем на более ранней стадии общечеловеческого развития он остановился. Самый гениальный наш математик: (судя по всему, имеется в виду Гаусс),- говорил А.Н. Колмогоров, остановился в возрасте четырех-пяти лет, когда “дети любят отрывать ножки и крылышки насекомым”. Себя А.Н. Колмогоров считал “остановившимся на уровне тринадцати лет, когда мальчишки очень любознательны и интересуются всем на свете, но взрослые интересы их еще не отвлекают”. 

Самодиагноз Андрея Николаевича с психологической точки зрения безупречен. Если учесть невероятную широту “посторонних” научных интересов математика Колмогорова - от гидродинамики до поведения в русской речи падежа, знать его литературные вкусы - от Евтушенко до Томаса Манна и Ахматовой, его культ дружбы и то особое место, которое в его жизни занимал спорт, то в этом случае возникает именно образ типичнейшего подростка. Но у Колмогорова есть еще одно условие для развития математической интуиции, необходимой для творчества. Впрочем, это условие некоторым образом связано с первым. Это обязательные для любого творческого ученого интересы, выходящие за рамки его профессии – прежде всего интересы в искусстве и литературе. (Конечно, в этом отношении Колмогоров не одинок. А. Эйнштейн много раз писал, что “Достоевский дает ему очень много, гораздо больше, чем Гаусс”).

Особое значение для Колмогорова имела музыка. Он считал, что “между математическим творчеством и настоящим интересом к музыке имеются какие-то глубокие связи”. Далее он ссылается на своего друга, П.С. Александрова, у которого “каждое направление математической мысли, тема для творческих размышлений связывались с тем или иным конкретным музыкальным произведением”. Решая вопрос, стоит ли брать какого-то студента или аспиранта в ученики, Колмогоров всегда принимал во внимание его нематематические, общекультурные интересы.

Следует отметить, что современные психофизиологические исследования подтвердили особую связь музыки и математики. Так, именно у выдающихся математиков и музыкантов были обнаружены так называемые “гармоники”, т.е. особые биоэлектрические показатели, определенным образом возникающие в ответ на стимуляцию мозга.

Обобщая выше сказанное, можно сделать следующие выводы:

1. По мнению Колмогорова, ускоренное (“вундеркиндное”) развитие не только не обязательно для достижения в будущем высокого профессионального (творческого) уровня, но в большей степени чревато возможностью неудач и даже психических отклонений. При диагностике математических способностей у детей категорически нельзя ориентироваться на темп развития и обучения.

2. Великий математик считал, что недопустима ранняя специализация способностей. Лишь с расцвета подросткового возраста (с 12-13 лет) можно начинать расширенное и углубленное обучение математике.

3. Для развития творческих способностей к математике, считает Колмогоров, необходимо выйти за пределы самой математики и развивать у ребенка, подростка или юноши общекультурные интересы, в частности, интерес к искусству (прежде всего - музыке) и поэзии.

В заключение хотелось бы добавить, что в способных детях таланты развиваются только в результате самостоятельной умственной работы, привычки преодолевать разные трудности. Такие условия дает самообучение и разумное одиночное обучение, не обучающее, но ободряющее и завлекающее. Полная самостоятельность в посильных вопросах, и своевременное разъяснение учителя в вопросах, превышающих силы ученика, способствуют развитию и воспитанию таланта.

Процесс развития математических способностей учащихся требует от учителя большого профессионализма. Для обеспечения эффективности своей деятельности педагог должен владеть разнообразными методами обучения, использовать в своей работе многочисленные приёмы и средства обучения. Его деятельность должна быть направлена на развитие самостоятельности и творческого потенциала в учениках. Поэтому для успешного осуществления своей деятельности учитель нуждается в разнообразных методических пособиях и рекомендациях, в обмене педагогическим опытом с другими учителями. В следующем разделе будут рассмотрены конкретные рекомендации по организации процесса развития математических способностей на уроке и внеклассных занятиях.

В подавляющем большинстве учебников и дидактических пособий для средней школы практически отсутствуют задачи, которые способствовали бы подготовке учеников к деятельности творческого характера и формированию у них соответствующих математических способностей. Математические знания учащихся слишком часто оказываются формальными и невостребованными, у основной массы учащихся не формируется разумный подход к поиску способа решения незнакомых задач.

Поэтому на уроках математики необходимо более активно заниматься развитием навыков в применении общих форм математической деятельности, таких, как:

• использование известных алгоритмов, формул, процедур;
• кодирование, преобразование, интерпретация:
• классификация и систематизация;
• правдоподобные рассуждения;
• выдвижение и проверка гипотез, доказательство и опровержение;
• разработка алгоритмов.

В данном разделе будут рассмотрены задачи разного уровня сложности, решение которых способствует развитию у учащихся навыков в использовании некоторых из выделенных выше общих форм математической деятельности.

К сожалению, в преподавании математики в российской школе по-прежнему доминирует формальный подход, связанный с отработкой конкретных методов решений. Существует такой тезис: “Если учащемуся предлагают упражнения только одного типа, выполнение каждого из них сводится к одной и той же операции, если эту операцию не приходится выбирать среди сходных и условия, данные в упражнении, не являются для учащегося непривычными и он уверен в безошибочности своих действий, то учащийся перестает задумываться об их обоснованности”. Этот тезис можно подкрепить описанием следующей психолого-дидактической закономерности: последовательность рассуждений (А, В, С ..... М), повторяющаяся при решении однотипных задач, может свертываться до составной ассоциации (А, М). Однако обратный процесс — развертывание — происходит без потерь не у всех учащихся.

Этот эффект хорошо известен составителям вариантов вступительных экзаменов в высшие учебные заведения: какова бы ни была по сути проста задача, но если ее решение предполагает использование двух различных (хотя бы и известных) алгоритмов или же если в нем должно содержаться некоторое исследование (к примеру, по параметру), то массовые ошибки неизбежны. Более того, ошибки часто появляются и в том случае, если алгоритм используется в ситуации, в которой он неприменим.

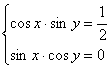
Решение этой задачи, как нетрудно видеть, сводится к цепочке простых логических рассуждений и использованию стандартных формул. Однако для того, чтобы получить правильный ответ, эти стандартные формулы следует правильно использовать. Не приводя ответ полностью, выпишем одну из четырех серий решений

К сожалению, слишком многие учащиеся бездумно отождествляют параметры k и n и вместо серии (1) пишут, что

упуская тем самым, условно говоря, большую часть решений этой серии.

Задача 1.2. Некоторое число умножили на 3, а затем к полученному произведению прибавили 2. Верно ли, что полученное число больше исходного?

Ясно, что За + 2 > а только при а > - 1, но какой процент, к примеру, семиклассников сразу даст верный ответ?

Реакция учащихся на последнюю из проводимых в этом разделе задач продемонстрирует степень их понимания стандартной схемы решения иррациональных уравнений.

Задача 1.3. Решите уравнение

Большая часть учеников начнет решение с нахождения ОДЗ и раскрытия модуля. А между тем можно сразу перейти к уравнению

Целесообразно задать учащимся такой вопрос: “Как вам кажется, какое уравнение проще решить, данное выше или уравнение ?”.

Простейшим примером использования указанных форм деятельности является их внутриматематическое применение, к примеру, замена переменной, перевод задачи с одного математического языка на другой (от алгебры к геометрии и обратно).

Кодирование или переформулирование способствует выявлению скрытых свойств объектов (существенных для данной задачи) путем включения их в другую систему связей. Использование разнообразных формулировок задачи способствует ее пониманию. Культура мышления предполагает развитое умение думать об одном и том же на разных языках.

Нужно уметь создавать и пользоваться различными моделями. А потому важно научить школьников формализовывать задачи и переводить условия и результаты с одного языка на другой, т.е. кодировать информацию, понимать смысл (т.е. интерпретировать) полученных в результате исследования результатов. Многие школьные задачи содержат в себе элементы кодирования, преобразования, интерпретации (к примеру, практически все текстовые задачи, но далеко не только они). Приведем примеры.

Задача 2.1. Докажите, что если от произвольного двузначного числа отнять двузначное число, записанное теми же цифрами в обратном порядке, то получится число кратное девяти.

Самая первая кодировка, с которой знакомятся школьники в процессе обучения математике, — это десятичная (позиционная) запись натуральных чисел. Если — исходное число, то , а число, “записанное теми же цифрами в обратном порядке”, равно , поэтому их разность кратна девяти.

Задача 2.2. Вычислите

Это число равно двум! Действительно, если положить , то получим выражение (а + 1)(а + 2) - а(а + 3) = а² +3а + 2 - а² - За = 2 вне зависимости от значения переменной а.

Конечно, тот же результат может быть получен, если записать каждую из входящих в данное выражение дробей в виде

и раскрыть скобки. При таком способе решения еще придется увидеть (не используя калькулятор), что 1997•1998 -1996 •1999 = 2.

Самое время сказать несколько слов о роли калькуляторов в обучении математике. Если он имеется у каждого учащегося в классе, то бессмысленно предлагать подобную единичную задачу; ясно, что ее математическое содержание останется нераскрытым. Необходимо дать несколько примеров, в каждом из которых ответ - 2, с тем, чтобы затем “разгадать загадку”.

Проверить это равенство легко, труднее найти аналогичные. Конечно, кто-то может сразу догадаться, что 8 = 3² - 1, и написать равенство

справедливость которого тоже очевидна. Однако, как и в предыдущем примере, основная идея - это введение замен (подстановок). Запишем равенство

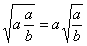
Его частными случаями являются равенства (2) и (3). В результате мы построили своего рода модель. Все что осталось сделать, — это исследовать ее, т.е. найти соотношение между а и b, при выполнении которого справедливо наше обобщенное равенство. А для этого надо провести простые преобразования:

Классификация — общепознавательный прием, суть которого заключается в разбиении данного множества объектов на попарно непересекающиеся подмножества (классы) в соответствии с так называемым основанием классификации, т.е. признаком, существенным для рассматриваемых объектов. Систематизация - это объединение объектов или знаний о них путем выявления существенных связей между ними, установление порядка между частями целого на основе определенного закона, правила или принципа.

Как писал У.У.Сойер: “Математика — это классификация и изучение всех возможных закономерностей”. Однако навыки в проведении классификации и систематизации необходимы далеко не только математикам, но инженерам и врачам, юристам и экономистам, менеджерам и т.д.

В математике часто встречается дихотомия, т.е. разбиение множества на два подмножества. Действительно, натуральные числа разделяются на простые и составные, действительные числа - на рациональные и иррационачьные, а иногда на алгебраические и трансцендентные. Целые числа можно различать по их остаткам при делении на какое-то число и т.д. и т.п. Естественнее всего классификация появляется при решении комбинаторных задач, однако наша первая задача из другой темы.

Часто встречается такой ответ: “Данное равенство верно в том случае, когда числа а и b имеют разные знаки”. Ответ не является полным, поскольку в нем ничего не говорится о том случае, когда одно из этих чисел обращается в ноль. Здесь допущена распространенная ошибка, которая заключается в неполноте проведенной классификации. В данном случае следует учитывать, что кроме положительных и отрицательных чисел, существует еще и ноль. Правильный ответ: при ab ? 0.

Задача 3.2. Сколькими способами можно расположить на шахматной доске (в соответствии с правилами шахмат) белого и черного королей?

Ответ: 4 • (64 - 4) + 24 • (64 - 6) + 36 • (64 - 9) = 3612 способами.

Введем систематизацию, различая случаи расположения одного из королей, например, черного. Именно, если черный король находится в одной из четырех угловых клеток, то, значит, имеется 64 - 4 = 60 возможностей для расположения белого короля. Если черный король стоит на краю доски, но не в углу (таких клеток 24), то имеются 58 вариантов для белого короля (из 64 клеток он не имеет права занимать саму клетку черного короля и еше 5 соседних, т.е. имеющих с ней общую сторону или вершину.) В оставшихся 36 случаях белый король может стоять на любой из 55 клеток, поскольку для него запрещены 8 клеток, соседствующих с клеткой черного короля, и сама эта клетка, т.е. 64 — 9 = 55.

Задача 3.3. Сколько различных (с точностью до положения в пространстве) каркасов треугольные пирамид можно составить, имея

Давайте составим таблицу, систематизирующую пирамиды по числу, например, зеленых стержней

Действительно, все пирамиды с одним зеленым ребром являются одинаковыми. Если зеленых рёбер два, то они могут быть либо смежными, либо скрещивающимися, поэтому в соответствующем месте стоит число “2”. Но не кажется ли странным число “4” в средней клетке этой таблицы? Ведь три зеленых стержня могут:

а) выходить из одной вершины;

б) образовывать треугольник;

в) образовывать незамкнутую пространственную ломаную.

Однако в последнем случае имеются две различные конфигурации, так сказать, правая и левая. На рис. изображены обе эти конфигурации, причем зеленые стержни обозначены толстыми линиями.

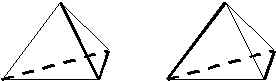
Таким образом, при помощи чисто комбинаторных рассуждений находим ответ: можно составить 12 пирамид.

Что можно сразу сказать о задаче пункта 2), так это то, что число вариантов не может быть большим, чем в случае 1), поскольку все равно, как различать ребра пирамиды: по цвету или же по длине — так что основания классификации одинаковы. Другое дело, что различаются сами множества пирамид, поскольку, к примеру, пирамиды, в одной из граней которой имеются два ребра длиной 10 см и одно — 20 см, не существует. В частности, аналогичная таблица не будет симметрична! Ответ: 5 различных пирамид.

Указанный в этом разделе подход к преподаванию математики может быть использован в школах различного профиля. И вполне возможно, что чем более, так сказать, гуманитарной является школа, тем сильнее следует подчеркивать нематематическую сторону дела, т.е. то, что методы и подходы, применяемые при решении конкретных математических задач, имеют чрезвычайно общий характер и связаны с процессом формирования и развития качеств мышления, необходимых для полноценного функционирования в современном обществе.

Внеурочные занятия по математике решают целый комплекс задач по углубленному математическому образованию, развитию индивидуальных способностей ученика, максимальному удовлетворению их интересов и потребностей.

Почему ученик занимается математикой вне занятий? В младшем возрасте это интерес к математике как любимому предмету, в среднем и старшем – это либо интерес к математике как науке, либо профессионально-ориентационный интерес, связанный с предполагаемой послешкольной деятельностью.

Среди задач, которые можно решать на внеклассных занятиях выделяются две категории внеучебных задач.

Первая категория. Задачи типа математических развлечений (занимательные задачи). По поводу этой категории Б.Л. Кордемский [11] пишет: “Первая категория внеучебных задач (очень пестрая по содержанию) прямого отношения к школьной программе не имеет и, как правило, не предполагает большой математической подготовки. Сюда входят задачи различной степени трудности и, прежде всего, начальные упражнения из цикла внешкольных упражнений, развивающих математическую инициативу, т. е. упражнения, предназначенные для тех, кто делает лишь первые шаги в мир математической смекалки.

Вторая категория. Задачи, примыкающие к школьному курсу математики, но повышенной трудности.

Рассмотрим каждую категорию отдельно.

Занимательные задачи в большинстве случаев содержат сюжет, доступный и понятный учащимся на начальных стадиях изучения математики. В структуре этих задач заложено проявление и развитие, например, таких параметров математических способностей, как догадка, смекалка, сообразительность, любопытство, любознательность и т. п.

В практике школы не предусмотрено решение задач занимательного характера непосредственно на уроке (нет прямого указания в программе, нет рекомендаций в методической литературе, отсутствует соответствующий материал в учебниках), в то время как для большинства людей, интересующихся математикой, первые живые впечатления от этой науки связываются с задачами или целыми книгами “развлекательного” плана. Задачи занимательного характера могут служить прекрасным способом вызывать у учащихся интерес к изучению математики.

Учитывая многообразие различного рода увлекательных, шутливых задач, для обеспечения целенаправленного и эффективного их использования необходима некоторая классификация занимательных задач.

Остановимся на классификации, предложенной одним из специалистов в области занимательных задач, Б.Л. Кордемским [10]. Заметим, что классификация ведётся согласно операционно-тематическому принципу - по сюжетам в сочетании с группами однородных операций - действий, применяемых для решения задач, объединенных темой. Согласно этому принципу выделяют следующие задачи:

1. “Затруднительные положения” (сюжетный стержень:
   физические действия, выполнение которых затруднено, но может быть осуществлено средствами математической смекалки).
2. “Геометрия на спичках” (сюжетный стержень: конструирование из спичек моделей фигур).
3. “Семь раз примерь, один раз отрежь” (сюжетный стержень: преобразование фигур при помощи перекраивания).
4. “Умение везде найдет применение” (сюжетный стержень: элементарно-технические и практические вопросы, решение которых требует участия математической мысли).
5. “С алгеброй и без нее” (сюжетный стержень безразличен, операционный стержень: алгебраический путь решения или любой иной, но всегда есть некоторая “изюминка” или в самом способе, или в сопоставлении способов решения).
6. “Математика почти без вычислений” (операционный стержень: действий почти нет, но для решения нужны искусные рассуждения).

Примеры занимательных задач будут содержаться в базе данных.

Особое значение имеют задачи, которые принято называть логическими. Основную, главную роль при решении таких задач играет правильное построение цепочки точных, иногда очень тонких, рассуждений. Термин “логическая задача” в методической литературе недостаточно четко определен. В большинстве случаев логическими задачами называют те, для решения которых необходимо лишь логическое мышление и не требуется математических выкладок. Поэтому их можно использовать для работы с учащимися различных классов без явной связи с материалом, изучаемым по школьной программе. Важно, что многие из задач такого рода носят занимательный характер. К сожалению, задач подобного рода практически нет на страницах школьных задачников. Их можно найти только в сборниках и книгах занимательного характера.

Среди широко распространенных логических задач выделим те, которые решаются способом так называемого “здравого рассуждения”, способом предположений, составлением различных таблиц, вычерчиванием графов. Один из наиболее элементарных, примитивных случаев состоит в применении способа перебора.

Рассмотрим задачи, которые можно считать логическими, но решение любой из них опирается на “здравый смысл”.

Задача 1. Крестьянину нужно перевезти через реку волка, козу и капусту. Как осуществить перевоз, чтобы волк не съел козу, а коза не съела капусту?

Схема рассуждений и ход решения.

Рассудительный ученик должен потребовать такое уточнение текста задачи: при крестьянине никто никого не ест! Без этого уточнения решать задачу невозможно.

Ознакомившись с текстом задачи, учащиеся могут сделать следующие выводы.

1. Крестьянин может сначала перевезти козу, оставив волка и капусту на одном берегу (волк не ест капусту!).
2. Крестьянин после этого может перевезти либо волка, либо капусту, но он должен с противоположного берега козу увезти назад, чтобы волк не съел ее, или она капусту. В этой комбинации перевоза козы назад и заключается необычность идеи, помогающей решить задачу.
3. После этого крестьянин перевозит соответственно капусту или волка.
4. Наконец крестьянин снова перевозит козу.

При решении данной задачи учащемуся прежде всего необходим “жизненный опыт”, так как решение задачи не предполагает каких-либо сложных математических выкладок. По-видимому, в данной задаче проявляется навык проведения логических рассуждений и характерных для дедуктивного мышления умений находить логические следствия из данных начальных условий. Конечно, при решении этой задачи и при решении любой другой, необходимы навык полноценной логической аргументации, стремление к ясности, простоте, экономности и рациональности решений.

При формировании аналитико-синтетической деятельности у учащихся представляют интерес так называемые задачи-головоломки или, как называет их английский профессор Смаллиан, - “дурацкие штучки”.

Приведем пример такой задачи.

Задача 2. Имеются две монеты на сумму 15 копеек. Одна из них не пятак. Что это за монеты?

Схема рассуждений и ход решения.

Практика показывает, что эта задача ставит в тупик человека достаточно часто, поскольку увидеть ответ не так уж легко. Это совершенно не страшно, надо просто подробно исследовать ситуацию. Как это делать?

1. На вопрос, какими могут быть две монеты, составляющие сумму 15 копеек, ответ для системы монет нашей страны однозначный: 10 копеек и 5 копеек.
2. Необычность формулировки задачи состоит в том, что указано: из этих двух монет одна не пятак, т. е. десятикопеечная, зато другая — пятак. При решении данной задачи должно проявиться такое качество мышления, как умение абстрагировать.

Нестандартность мышления проявляется и при решении таких задач, в которых встречаются слова одного рода, а подразумевается противоположный пол. Например, такая задача.

Задача 3. Сын отца полковника беседовал с отцом сына полковника. Кто с кем беседовал, если полковника при этом не было?

Схема рассуждений.

Стандартное понимание слова “полковник” приводит к стереотипному выводу, что полковник — мужчина, но в задаче “полковник” — женщина, т. е. брат полковника беседовал с мужем полковника.

Выше отмечалось, что приведенные задачи требуют для своего решения определенного “здравого смысла”, но следует указать и на такие задачи, которые содержат в условиях очень много данных. Удерживать в памяти все факты, приведенные в условиях задачи, трудно, поэтому следует использовать вспомогательные записи или таблицы. Эти записи помогают исключить из рассмотрения нерешаемые варианты (противоречащие условию). Ниже приведены задача, решение которых требует использования вспомогательных таблиц.

Задача 4. Олег, Игорь и Оля учатся в одном классе. Среди них есть лучший математик, лучший спринтер и лучший художник класса. Известно, что:

В задаче речь идет о двух множествах (множество школьников и множество специальностей). Воспользуемся таблицей 3x3 клетки.

Из первого условия задачи следует, что Игорь не художник, ставим в таблице “-”, во второй строке и в третьем столбце. Из второго условия следует, что Оля лучший спринтер и поэтому ставим знак “+” в третьей строке и во втором столбце, значит Оля не художник. Игорь не художник, художник — Олег, а лучшим математиком может быть только Игорь. Наглядно показано, что таблица значительно облегчила решение задачи.

Иногда приходится составлять таблицы с большим числом входов или рассматривать несколько таблиц. В этом случае можно использовать графы. Иногда граф может играть вспомогательную роль в сочетании с другими методами решения.

Графом называют схему (сетку, карту), составленную из нескольких точек, называемых вершинами графа, и нескольких отрезков (или дуг), соединяющих эти точки и называемых ребрами графа.

Применяя граф к решению логических задач, вершинам и ребрам графа обычно придают определенный смысл. Часто решение задачи получается наглядным и эффективным. Примером решения с использованием графов может служить следующая задача.

Задача 5. Студенты педагогического университета организовали эстрадный квартет. Михаил играет на саксофоне. Пианист учится на физическом факультете. Ударника зовут не Валерием, а студента географического факультета зовут не Леонидом. Михаил учится не на историческом факультете. Андрей не пианист и не биолог. Валерий учится не на физическом факультете, а ударник - не на историческом. Леонид играет не на контрабасе. На каком инструменте играет Валерий и на каком факультете он учится?

Схема рассуждений и ход решения.

В этой задаче имеется три множества (студенты, инструменты, факультеты) по четыре элемента в каждом. Составление таблиц громоздко (придётся чертить три таблицы) и неэффективно. Воспользуемся графами. Обозначим студентов первыми буквами их имен: М, А Л, В; инструменты, на которых они играют: С, П, У, К; факультеты, на которых они учатся: Ф, Г, И, Б. Будем соединять элементы двух множеств сплошной линией, если между ними установлено взаимно однозначное соответствие, и пунктирной линией, если такое отсутствует.

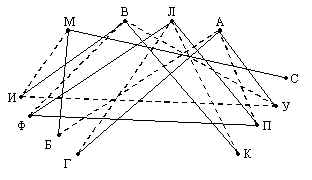
Пианист учится на физическом факультете, им может быть Леонид, потому что Андрей не пианист, Михаил играет на саксофоне, а Валерий не учится на физическом факультете. Тогда Андрей — ударник, так как Валерий — не ударник, и Андрей учится на географическом факультете, потому что ударник учится не на историческом и Андрей — не биолог. Михаил - биолог, а Валерий играет на контрабасе и учится на историческом факультете.

При отборе задач, предназначенных для той или иной цели, необходимы требования, которым бы отвечала выбранная система задач. Например, Ю.М. Колягин предъявляет следующие требования к задачам, которые могут быть использованы для развития гибкости мышления:

а) допускают несколько способов решения;

б) требуют конструирования нового способа из ранее изученных, применения вспомогательных приемов;

в) требуют необычного способа решения, при этом полезно
завуалировать необходимость необычного способа таким содержанием и структурой, которые по виду напоминают обычную стандартную задачу;

г) решаются известным способом, но необычное содержание задачи маскирует этот способ.

В качестве примера таких задач приведу систему заданий для учащихся 7-9 классов по углубленному изучению курса математики, разработанную Салюковой Светланой Васильевной – учителем математики высшей категории средней школы №4 г. Сорочинска [21]. Данная система разработана на основе технологии развивающего обучения и способствует развитию у учащихся математических способностей. Задания вводятся во внеучебное время, учащиеся могут выполнять их либо самостоятельно, либо с помощью учителя, родителей, учеников старших классов. Один раз в неделю учитель проводит консультации по выполнению предложенных заданий.

Сама система заданий представлена в приложении 2. Она включают опорные знания и умения базовой программы. Вместе с тем углубленное обучение с помощью этой системы заданий имеет свои особенности:

• необходимо на основании диагностических исследований производить отбор учащихся: за трехлетний цикл учебы в 7-9 классах данную систему заданий могут усвоить в полном объеме только хорошо подготовленные ученики;
• в системе заданий учтено, что у учащихся 7 класса не сформировано целостное представление о математике как науке;
• задания тесно связаны, переплетены с тем, чем учащиеся занимаются на уроках алгебры и геометрии;
• при выполнении заданий учащимся помогают специальные опорные конспекты по каждой теме, составленные на уроке;
• при организации работы по предложенной системе заданий необходимо проявлять доверие к силам ребенка, диалог учителя и ученика на равных;
• при обучении по предложенной системе заданий вся работа направлена на создание условий для активной, познавательной деятельности, для самостоятельного добывания знаний учащимися, когда требуется самостоятельное осмысливание материала, высказывание собственного мнения об изучаемом, анализ способов познания тех или иных тем.

Разработанная система заданий по математике позволяет:

- максимально использовать резервные возможности в развитии математических способностей каждого ученика;

- добиться быстрого и основательного усвоения углубленных программных знаний с экономией учебного времени;

- повысить интеллектуальный уровень учащихся;

- сформировать навыки выполнения умственных операций;

- повысить качество подготовки школьников по математике.

Основополагающим в процессе развития математических способностей является грамотный подбор задач. Видов задач большое количество, каждая задача выполняет свою отдельную функцию (чаще даже несколько функций). Так занимательные задачи направлены на формирование познавательного интереса к изучению математики, развивают математическую смекалку. Задачи повышенного уровня сложности предназначены для более глубокого, вдумчивого, осмысленного понимания пройденных тем школьного курса математики. В учебных пособиях наблюдается дефицит нестандартных задач, решение которых требует от учеников умственного напряжения, проявления самостоятельности и творчества. Такое многообразие задач требует от учителя так называемой “задачной эрудиции”. А ведь не каждый учитель, особенно начинающий, может похвастаться большим “банком задач” или умением их грамотно отбирать. Для решения этих проблем и предназначена база данных, описанию которой посвящена следующая глава.

Основу всей базы данных составляют методические разработки по развитию математических способностей. Так как способности развиваются только в процессе специально организованной деятельности, в нашем случае при решении математических задач, то в основном методические разработки представляют собой различные комплексы задач; хотя возможности базы данных не исключают хранение различных обучающих программ, демонстрационных роликов, конспектов уроков и т.п.(OLE-объектов).

В основном все данные хранятся в таблице “Главная”. Эта таблица имеет следующие поля:

• “Тема”: содержит информацию о тематике или название методической разработки;
• “Класс”: содержит информацию о том, для какого класса предназначена данная методическая разработка;
• “Вид способностей”: содержит информацию о том, какой вид математических способностей развивает данная методическая разработка;
• “Вид занятия”: содержит информацию о том, на каком занятии лучше всего реализовать данную методическую разработку;
• “Источник”: содержит информацию о том, откуда была взята методическая разработка, кто её автор;
• “Количество заданий”: содержит информацию о количестве заданий в методической разработке;
• “Аннотация”: содержит краткое содержание или первичную ознакомительную информацию о методической разработке;
• “Ключевые слова”: это поле предназначено главным образом для осуществления поиска в базе данных; оно содержит слова, отражающие суть методической разработки, по которым пользователь, возможно, будет осуществлять поиск.
• “Задания”: содержит непосредственно файл (чаще всего документ Word) с заданиями из методической разработке. Фактически здесь содержится то, что предоставляется ученику учителем.
• “Задания с решениями”: содержит файл со всей методической разработкой в целом (задания, их решения, методические рекомендации), то есть весь материал для организации работы учителя.

Ещё в состав базы данных входят 3 вспомогательные таблицы.

Таблица “Классы” содержит всего два поля: “Класс” и “Выбор”. Она предназначена для более удобного внесения данных в “Главную” таблицу (выпадающий список) и осуществления многовариантного поиска по фиксированным параметрам. Записи в этой таблице строго зафиксированы, их 6: классы с пятого по девятый и запись “Любой класс”. “Любой класс” означает, что данная методическая разработка может быть осуществлена в любом классе, так как её содержание не связано с вопросами школьной программы по математике (логические задачи, занимательные задачи). Следует учитывать, что выбор класса носит рекомендательный характер, а не строго установленный, и то, что например, рекомендовано для пятого класса, можно использовать и в шестом классе (с некоторыми поправками).

Таблица “Вид способностей” также как и таблица “Классы” предназначена для более удобного внесения данных в “Главную” таблицу и осуществления многовариантного поиска по фиксированным параметрам. Записи в ней также зафиксированы, их 5: арифметические, алгебраические, геометрические, логические, смешанные. Так как классификаций математических способностей очень много, не существует одной устоявшейся, то я поделила (конечно, очень грубо) способности на арифметические, алгебраические, геометрические, логические, в зависимости от материала, с которым мы оперируем при решении задач по развитию этих способностей – числа, алгебраические выражения, фигуры, логические рассуждения. Большинство методических разработок развивают целый комплекс математических способностей, в этом случае выбирается смешанный вид способностей.

Таблица “Вид занятия” аналогично предшествующим таблицам предназначена для более удобного внесения данных в “Главную” таблицу и осуществления многовариантного поиска по фиксированным параметрам. Она содержит 3 фиксированные записи: урок, факультатив, внеклассное занятие. Здесь следует учитывать, что предположительно внеклассное занятие по математике должно проводится во всех классах с целью развития познавательного интереса к этому предмету, формирования внутренней мотивации учения, поэтому методический материал носит познавательный, занимательный характер; а вот на факультатив ученики ходят по собственному желанию для серьёзного, более глубокого изучения математики, следовательно, задания в методической разработке имеют повышенный уровень сложности.

При запуске программы пользователь попадает на главную загрузочную форму базы данных “База данных по развитию математических способностей” (см. Приложение 3). С её помощью он может перемещаться по другим формам база данных. На загрузочной форме представлена информация о названии базы данных, её авторе и расположены следующие кнопки перехода к другим формам базы данных:

• “Ознакомительная информация”,
• “Поиск данных”,
• “Добавление данных”,
• “Справочная информация”,
• “Завершение работы”.

В форме “Ознакомительная информация” содержится информация о назначении базы данных, её возможностях.

Форма “Поиск данных” позволяет осуществлять различные виды поиска: поиск по фиксированным параметрам и расширенный поиск (подробнее см. следующие разделы). Для каждого вида поиска определена своя закладка на форме. При загрузке формы пользователь по умолчанию попадает на закладку “Поиск по фиксированным параметрам”. Чтобы перейти к другому виду поиска надо щелкнуть мышкой по закладке “Расширенный поиск” в верхнем левом углу формы. Результаты поиска по фиксированным параметрам предоставляются пользователю на отдельной форме “Результаты поиска”.

Форма “Добавление данных позволяет вносить пользователю новые данные в базу данных.

Чтобы грамотно осуществлять поиск нужной информации или добавлять данные в базу данных, пользователю необходимо ознакомится с правилами выполнения этих операций. Эти правила содержаться в форме “Справочная информация”. Каждая из перечисленных форм закрывается с помощью кнопки “Выход”. После нажатия этой кнопки, пользователь попадает на главную загрузочную форму базы данных. По завершению работы с базой данных, для её закрытия пользователь должен щёлкнуть по кнопке “Завершение работы” на главной форме.

При добавлении данных пользователь заполняет соответствующие поля таблицы “Главная”: “Тема”, “Класс”, “Вид способностей”, “Вид занятия”, “Источник”, “Количество заданий”, “Аннотация”, “Ключевые слова”, “Задания”, “Задания с решениями”. Все эти поля являются обязательными для заполнения.

Подробно хотелось бы описать заполнение полей “Задания” и “Задания с решениями”, так типом этих полей является OLE-объект, и пользователю для их заполнения придётся пользоваться пунктом меню “Вставка”. Итак, для заполнения полей “Задания” и “Задания с решениями” надо выполнить следующие операции:

1. поместите файлы с методическими разработками в папку Data, которая находится в той же папке, что и файл базы данных;
2. откройте базу данных и форму “Добавление данных”;
3. установите курсор в то место формы, куда вы хотите вставить данные;
4. выберете команду “Объект” из меню “Вставка” и щёлкните на переключатель “Создание из файла” диалогового окна “Вставка объекта”;
5. установите флажок “Связь с файлом”, щёлкните на кнопке “Обзор”, чтобы найти файл;
6. если вы добавляете данные в поле “Задания с решениями”, то установите флажок “В виде значка”;
7. нажмите на кнопку “OK”.

1. Поиск по фиксированным параметрам.

База данных предоставляет возможность осуществлять поиск по трём параметрам: класс, вид занятия и вид способностей. По каждому из параметров выберете необходимые компоненты, щёлкнув мышкой по полю “Выбор”, и нажмите кнопку “Выполнить поиск”. Существует два вида поиска по фиксированным параметрам: строгий и нестрогий. При строгом поиске будут отбираться записи, у которых совпадают все три заданных параметра, а при нестрогом – хотя бы один параметр из трёх. Результаты поиска предоставляются пользователю на отдельной форме “Результат поиска”, которая содержит кнопку расширенного поиска (кнопка с нарисованным биноклем), то есть по отфильтрованным записям можно будет осуществить расширенный поиск. Если не будет найдена ни одна запись, удовлетворяющая заданным параметрам, то высветится пустая форма.

2. Расширенный поиск.

С помощью расширенного поиска можно найти записи, содержащие определённый фрагмент информации. Для поиска в одном поле формы, проделайте следующие шаги:

1. Выделите любое поле, в котором вы хотите провести поиск, щелкнув на нем мышкой, и нажмите кнопку “Поиск”.

2. В текстовом поле “Образец” на вкладке “Поиск” напечатайте текст, который вы хотите найти.

3. Убедитесь, что в раскрывающемся списке “Поиск в” выбрано название столбца, а в раскрывающемся списке “Совпадение” указано “Поля целиком”. (Эти параметры будут пояснены позднее.)

1. Щелкните на кнопке “Найти далее”. Access начнет поиск с первой записи таблицы и выделит первое найденное совпадение (или поместит на экран сообщение, что совпадений не обнаружено), .
2. После того как первое совпадение найдено, щелкайте на кнопке “Найти далее” для поиска каждого последующего совпадения. Можно также закрыть диалоговое окно “Поиск” и нажимать комбинацию клавиш Shift+F4 для поиска следующих совпадений.

Расширенный поиск можно настраивать. Если вы хотите, чтобы поиск был осуществлен по всем полям таблицы, укажите параметр “Главная” в раскрывающемся списке “Поиск в”. Можно контролировать направление поиска, выбрав соответствующий параметр в раскрывающемся списке “Просмотр”. Если вы устанавливаете параметр “Все”, Access будет просматривать все записи. Поиск осуществляется от выделенной записи вниз до конца таблицы, а затем от начала таблицы вниз до записи, предшествующей выделенной. Если вы выбрали параметр “Вниз”, Access производит поиск от выделенной записи вниз до конца таблицы и прекращает его. Если вы выбираете параметр “Вверх”, поиск осуществляется от выбранной записи вверх до начала таблицы и прекращается. Значения из раскрывающегося списка “Совпадение” определяют, каким образом Access ищет совпадения в каждом поле. Возможные варианты перечислены в таблице.

Можно использовать другие элементы управления диалогового окна для более точного определения, как Access должен искать совпадающее значение. При установке флажка “С учетом регистра” Access найдет совпадения только для тех фрагментов текста, где соблюдается регистр всех букв.

1. Работа с найденными записями.

В результате поиска будут найдены записи, содержащие необходимые методические разработки. Фрагмент этих методических разработок высветится в поле “Задания”. Чтобы просмотреть методические разработки полностью щёлкните два раза мышкой по полю “Задания” или “Задания с решениями”. Внимание! Допускается копирование данных, но не их изменение или удаление!

3.3. Апробация базы данных

Разработанная база данных была апробирована на базе средней школы №34 (её просмотрели 5 учителей математики и 2 учителя информатики). С учителями было проведено анкетирование по следующим вопросам:

1. Проводите ли Вы целенаправленную работу по развитию математических способностей учащихся?
2. Ощущаете ли Вы дефицит дидактического материала по развитию математических способностей?
3. Использовали бы Вы предложенную базу данных в своей практике?
4. Существует ли потребность в такого рода программных продуктах?
5. Удобен ли интерфейс программы? (Проста ли база данных в использовании?)
6. Ваши замечания, рекомендации, предложения.

Результаты анкетирования: по первым пяти вопросам все учителя единогласно дали ответ “Да”. Такие результаты подтверждают актуальность и востребованность разработанного программного продукта, доказывают справедливость выдвинутой гипотезы.

Среди замечаний и предложений можно выделить следующие:

• расширение базы данных за счет увеличения числа методических разработок;
• бесплатное распространение базы данных по школам.

По итогам анкетирования база данных была дополнена новыми заданиями в размере 103 задач. Что же касается бесплатного распространения, то конечно же я оставила копию базы данных в школе, хотя мне хотелось бы отметить достаточно низкий уровень компьютерной грамотности учителей и их настороженность, “боязнь” современных информационных технологий.

Задача всестороннего и гармонического развития личности делает совершенно необходимой глубокую научную разработку проблемы способностей школьников. Разработка этой проблемы представляет как теоретический, так и практический интерес.

Проблема способностей – это проблема индивидуальных различий. Каждый человек к чему-нибудь оптимально способен, но способности людей не одинаковы. Каждый человек более способен к одним и менее способен к другим видам деятельности. Это ставит перед школой задачу максимально возможного развития всех способностей ученика, уделяя при этом внимание развитию главной, ведущей способности, как основы его будущеё профессиональной направленности. Итак, учитель математики на своих уроках должен развивать математические способности учеников, при этом учитывать возможности и интересы каждого из них.

Как же развиваются способности? Способности не есть нечто раз навсегда предопределённое, они формируются и развиваются в процессе обучения, в процессе упражнения, овладения соответствующей деятельностью. Если к этому добавить принцип учета индивидуальных и возрастных особенностей учащихся, то мы сталкиваемся с проблемой недостатка методической информации, в частности дидактических материалов.

Эта проблема легко решается, если использовать современные информационные технологии. Разработанная мною база данных предоставляет учителю готовые методические разработки по развитию математических способностей и позволяет осуществлять быстрый автоматический поиск необходимой информации. Таким образом, цель своей дипломной работы я считаю достигнутой, а гипотезу подтверждённой. Но это не означает, что база данных способна решить все проблемы по развитию математических способностей.

Во-первых можно наметить некоторые пути усовершенствования базы данных. Так как педагогика не стоит на месте, то база данных нуждается в регулярном пополнении новыми методическими разработками, для этого и была разработана функция добавления данных. Процесс развития способностей не отделим от процесса диагностики этих способностей, поэтому идеально было бы объединить базу данных с автоматизированной системой тестирования, которая бы по результатам теста автоматически находила в базе данных необходимые задания по развитию математических способностей.

Во-вторых, если учитель не знаток своего дела, то никакая база данных не разовьёт способности у его учеников. В процессе развития способностей главенствующую роль играет учитель, его профессионализм, а база данных – лишь инструмент, облегчающий его работу. Поэтому для процесса развития способностей так важна личность учителя, его жизненная позиция. Только педагог с активной жизненной позицией, постоянно занимающийся личным и профессиональным самосовершенствованием, постигающий новые педагогические технологии, методы и приёмы может достичь высоких успехов в процессе развития математических способностей своих учеников.

1. Верно ли, что для любых чисел a и b выполняются условия

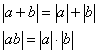
2. Известно, что . Верно ли, что ?

3. Известно, что . Запишите в виде двойного неравенства, что среднее арифметическое чисел a и b заключено между числами a и b.

4. При каких значениях коэффициента m уравнение mx=5 имеет единственный корень? Существует ли такое значение m, при котором это уравнение не имеет корней? Имеет бесконечно много корней?

5. Решите уравнения:

а) (х+2)(х-9) = 0

б) (х+1)(х-1)(х-5) = 0

6. Не решая уравнения 7(2х+1)=13 докажите, что его корень не является целым числом.

7. При каких значениях а уравнение ах = 8 имеет а) корень, равный -4; б) не имеет корней; в) имеет отрицательный корень.

8. При каком значении а точка А (а; -1) принадлежит графику функции у=3,5х

9. Задайте формулой линейную функцию, графиком которой служит прямая, проходящая через точку А(2;3) и параллельная графику функции у=1,5x - 3

10. Докажите, что уравнение не имеет положительных корней.

11. Точка А(a;b) принадлежит графику функции у=х•х. Принадлежат ли этому графику точки В(-a;b), C(a; -b), D(-a; -b).

12. Докажите, что сумма чисел и кратна сумме a и b.

13. Трехзначное число оканчивается цифрой 7. Если эту цифру переставить на первое место, то число увеличивается на 324. Найти трехзначное число.

14. Докажите, что значение выражения а•а - а кратно 2 при любом целом значении а.

15. Решите уравнения:

1. Докажите, что (а+1)(b+1) – (а-1)(b-1) =18, если а+ b=9

2. Представьте в виде произведения:

а) (х+1)³ + х³;

б) 27а³ – (а - b)³.

3. Решите уравнение х³ - 2х² - х + 2 = 0.

4. Постройте график уравнения

а) (х-2)(у-3) =0

б)

5. При каком значении k система имеет единственное решение?

6. Написали два числа. Если первое число увеличить на 30%, а второе уменьшить на 10%, то их сумма увеличится на 6. Если же первое число уменьшить на 10%, а второе на 20%, то их сумма уменьшится на 16. Какие числа были написаны?

7. Построить треугольник:

а) по двум сторонам и высоте, проведенной из одной вершины;
б) по углу, высоте и биссектрисе, проведенным из вершины этого угла;
в) по стороне, медиане, проведенной к этой стороне, и высоте, опущенной на другую сторону;

г) по острому углу и двум высотам, проведенным к сторонам, образующим данный угол.

8. На продолжениях медиан BM и CN треугольника ABC за точки M и N отложены отрезки MP и NQ, соответственно равные BM и CN. Докажите, что прямая PQ проходит через точку A.

9. Медиана AM треугольника ABC перпендикулярна его биссектрисе BK. Найдите AB, если BC=12.

10. Один из углов треугольника равен a. Найдите угол между биссектрисами двух других углов.

11. Острый угол прямоугольного треугольника равен 30 градусам, а гипотенуза равна 8. Найти отрезки, на которые делит гипотенузу высота, проведенная из вершины прямого угла.

1. Построить графики следующих функций:

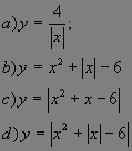
2. При каких целых значениях n значение выражения является натуральным числом?

3. Упростить выражения:

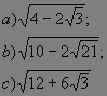
4. Решите уравнения:

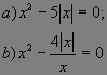
5. При каких значениях параметра а один из корней уравнения (а² - 5а + 3)•х²+ (3а - 1)•х + 2 = 0 в два раза больше другого?

6. При каких значениях параметра b уравнение х² + bх + 4 = 0: а) имеет один из корней, равный 3; б) имеет различные корни; в) имеет один корень; г) не имеет корней?

7. Сторона треугольника равна а. Найдите отрезок, соединяющий середины медиан, проведенных к двум другим сторонам.

8. Докажите, что расстояние от вершины треугольника до точки пересечения высот вдвое больше, чем расстояние от центра описанного круга до стороны, противолежащей этой вершине.

9. Найти отношение оснований трапеции, если ее средняя линия делится диагоналями на три равные части.

10. Радиус окружности, описанной около равнобедренного треугольника, равен R. Угол при основании равен a. Найдите стороны треугольника.

Рис. 1 Главная загрузочная форма базы данных.

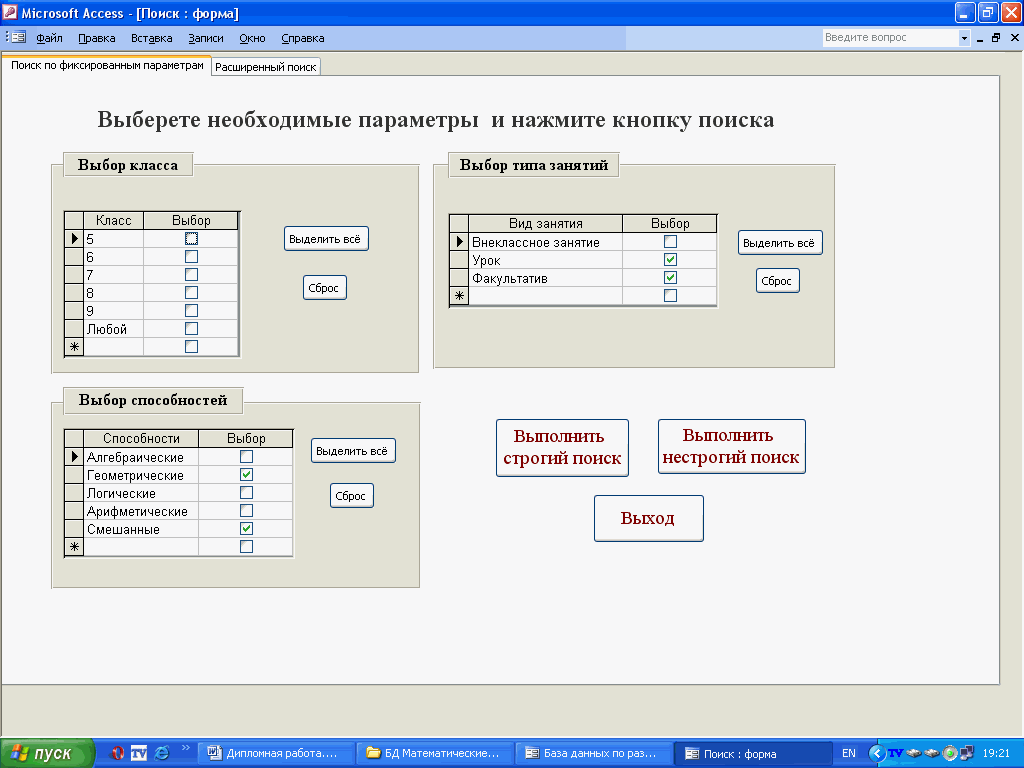
Рис. 2 Форма поиска данных.

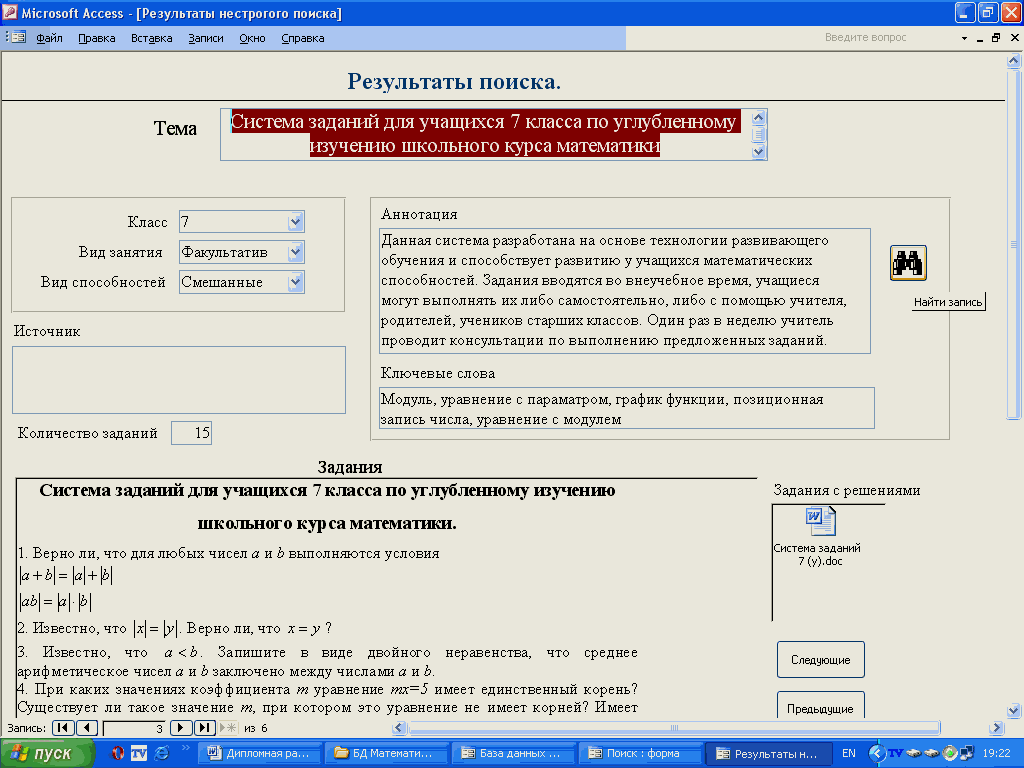
Рис. 3 Форма результатов поиска.

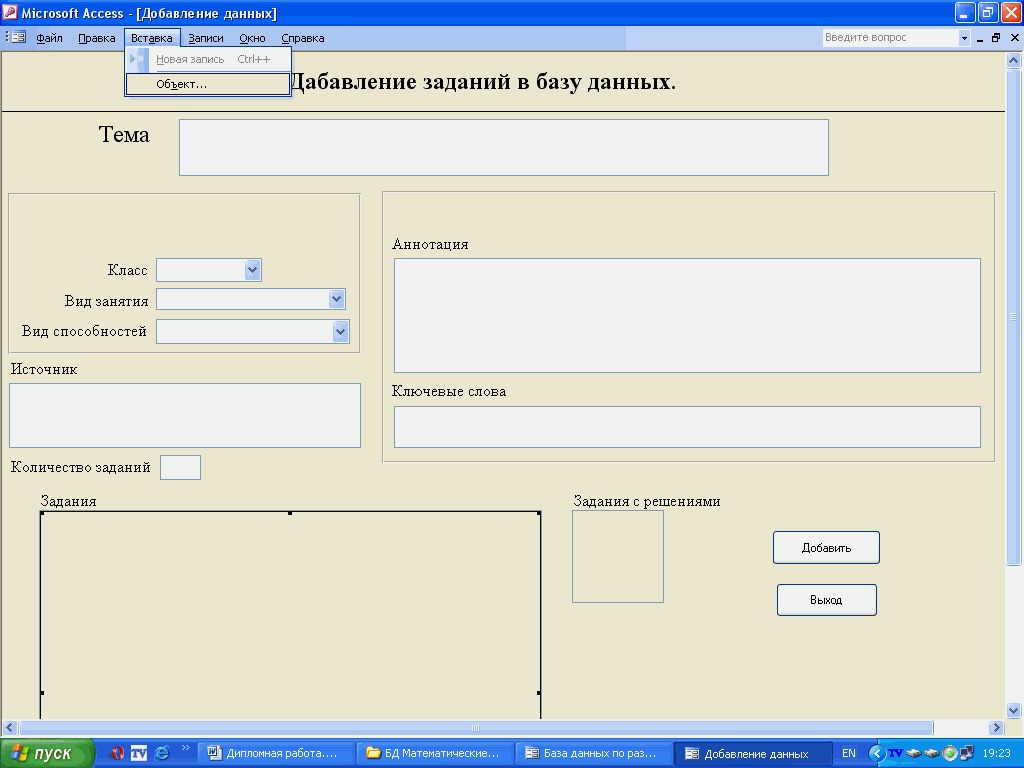
Рис. 4 Форма добавления данных.

Рис. 5 Форма со справочной информацией.