УДК 531/534:57+621.7
Расчет
нагрузки в области тазового кольца
© 2006 г. Серов М.
А.*, Родионов А. А., Шатохин Н. В.**
В работе проанализировано взаимодействие сил,
действующих со стороны мышечной ткани тазовой кости и гравитационных сил в
области вертлужной впадины во время ходьбы. Для реализации биомеханических исследований
была применена трехмерная модель тазовой кости и использован программный
комплекс MSC Nastran for Windows v4.0
Ключевые
слова: Тазовое кольцо, трехмерная модель, мышечная ткань, гравитационные силы,
биомеханика, моделирование.
Введение
В тазовом кольце основные линии напряжений известны, но общая картина распределения
напряжений внутри костной ткани остается до сих и неясной. Это является
препятствием для развития новых ортопедических методов по репозиции костей
таза.
Основная причина неясности заключается в частичном или полностью не
учитываемом факторе влияния мышечных усилиий на распределение напряжений в
тазовом кольце. Это является следствием проведения экспериментов, как по
изучению, так и внедрению новых аппаратов внешней фиксации при переломах
тазового кольца, на трупном материале, который не обладает таким характерным
для организма функциями, как сокращения мышечной ткани.
Постановка задачи
Целью данной работы является исследование силового воздействия в костной
ткани при помощи трехмерной модели тазовой кости тазового кольца.
В данной работе рассматриваются вопросы:
1) на каком уровне и как компенсируются силовые нагрузки, как со стороны
действия мышц, так и со стороны веса человека, так как до коленного сустава и
стопы они практически не доходят;
2) как будет действовать обобщенный вектор рассматриваемых сил, если за
точку приложения этого вектора выбрана область вертлужной впадины;
3) как согласуются сведения о размерах нагрузки с биомеханическими
свойствами костной ткани и предполагаемыми линиями силового напряжения;
Для анализа биомеханических свойств костной ткани при помощи пакета
автоматизированного проектирования SolidWorks была создана трехмерная компьютерная модель
тазовой кости [1]. Расчеты были произведены в программном комплексе Nastran.
Модель представляет собой конечномерную систему состоящую из 2662
элементов и 1982 узлов. Модуль Юнга и Пуассона соответственно были приняты 17
ГПа и 0,3 – для кортикального слоя и 800 МПа и 0,2 – для трабекулярного слоя.
Нагрузка для костной ткани была выбрана в виде динамически изменяющиеся
во время ходьбы силы. Точками приложения сил являются области прикрепления
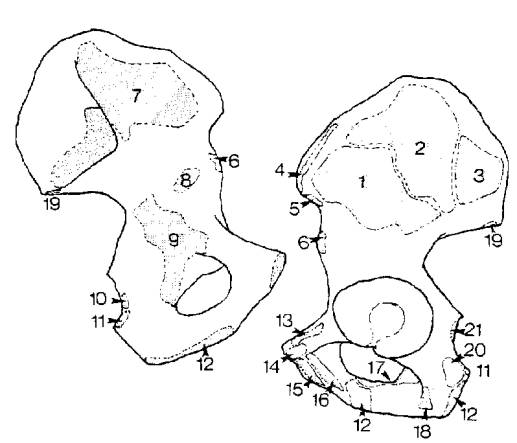
мышечных тканей к кости (число таких мест составило 21 (см. рис. 1), исходя из
анатомических особенностей строения костей тазового кольца).
1. m. gluteus minimus
2. m. gluteus medius
3. m. gluteus maximus
4. m. tensor fascia lata
5. m.
sartorius
6. m. rectus femoris
7. m. iliacus
8. m. psoas
9. m. obturator internus
10. m. gemellus inferior
11.
m. semitendinosus
12. m. adductor magnus
13. m. pectineus
14. m. adductor longus
15. m. gracilis
16. m. adductor brevis
17. m. obturator externus
18. m. quadratus femoris
19.
m. piriformis
20. m. Semimembranosus
21. m. gemellus superior
Рис. 1. Зоны прикрепления мышц и их
названия
За период ходьбы была взята величина, состоящая из двух полупериодов:
наличия сил действующих со стороны веса при одноопорной нагрузки и их
отсутствия при переносе веса тела на другую ногу [2]. В свою очередь каждый
полупериод был разделен на четыре позиции. Описание каждой фазы представлено в
таблице 1.
Таблица 1 – Основные фазы ходьбы
|
Номер
позиции |
Название
позиции |
Процент
действия фазы |
Изменение
угла наклона бедра |
|
1 |
Двухопорная
позиция |
3 |
22 (внутрь) |
|
2 |
Одноопорная
позиция с весом (начальная фаза) |
10 |
18 (внутрь) |
|
3 |
Одноопорная
позиция с весом (средняя фаза) |
22 |
4 (внешний) |
|
4 |
Одноопорная
позиция с весом (конечная фаза) |
13 |
12
(внешний) |
|
5 |
Двухопорная
позиция |
3 |
14
(внешний) |
|
6 |
Одноопорная
позиция без веса (начальная фаза) |
14 |
2 (внутрь) |
|
7 |
Одноопорная
позиция без веса (средняя фаза) |
22 |
31 (внутрь) |
|
8 |
Одноопорная
позиция без веса (конечная фаза) |
13 |
21 (внутрь) |
Угол наклона между бедренной костью и тазовым кольцом составляет 15
градусов. Вес среднестатистического человека без учета веса ног составляет 65 кг,
поэтому за вес тела была принята величина 650 Н.
Величины действия сил со стороны мышц были взяты из исследований
проведенных Crowninshield в 1981 году. Было получено экспериментально действие
сил путем измерения площади сечения и измерением величины силы действующей в
одной единицы площади мышечной ткани. Величина действия этих сил в зависимости
от позиции человека, занимаемой при ходьбе, приведена в таблице 2.
Таблица 2 – Величины сил (в Ньютонах)
|
Название
мышц |
Величина сил,
действующих со стороны мышц в каждой фазе |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
Бедро 1.Gluteus maximus
2.Gluteus medius 3.Gluteus minimus 4.Tensor fasciae latae 7.Iliacus 8.Psoas 15.Gracilis 5.Sartorius 20.Semimembranosus 11.Semitendinosus
Biceps femoris longus 14.Adductor longus 12.Adductor magnus 16.Adductor
brevis 17.Obturator externus 9.Obturator internus 13.Pectineus 19.Piriformis 18.Quadratus
femoris 21.Superior gemellus 10.Inferior gemellus 6.Rectus femoris |
426 842 1018 228 0 0 149 0 0 579 0 298 0 0 0 0 167 0 202 61 140 0 0 |
2158 930 1053 140 132 0 0 0 88 368 140 202 88 0 114 0 123 0 275 96 88 0 123 |
1876 167 1474 263 88 0 316 0 0 333 105 88 0 0 0 0 0 175 0 0 123 0 0 |
1651 377 1509 228 158 228 175 0 0 368 246 70 0 0 0 0 61 96 0 0 79 0 0 |
1180 456 1412 175 149 307 88 88 35 421 316 123 88 132 0 123 61 0 0 88 0 0 0 |
187 491 982
123 88 272 175 158
158 298 368 114 158 263 202 167 149 149 0 184 0 140 175 |
87 114 105 114 70 0 105 70 88 61 105 79 70 0 0 132 123 0 123 0 158 79 105 |
379 482 421
219 96 0 140 140 88 421 0 377 140 0 114 123 0 0 228 0 202 149 96 |
Метод решения
Построение векторов действия сил со стороны мышц, производилось с учетом
направления расположения продольных мышечных волокон, которые являются составной
частью отдельных групп мышц описанных ранее. Обозначим величину действия сил со
стороны мышечной ткани через F. С учетом направления расположения
продольных мышечных волокон, схема действий основных векторов мышечных сил
представлена на рисунке 2. На основе полученной схемы создаем проекции каждого
вектора на оси системы координат, в результате получим следующие величины F(x), F(y), F(z). Выделяем
плоскости, которые будут необходимы для построения проекций: XY, XZ, YZ, а углы
соответствующих проекций обозначим через α, β, γ. Значения величин углов по каждому из векторов сил, оказываемых со
стороны мышц, представлены в таблице 3.
Построение данных проекций производим следующим образом:
-
выбираем одну из плоскостей проекций (XY, XZ, YZ);
-
вычисляем величину проекции в зависимости от плоскости
проекции по следующей схеме:
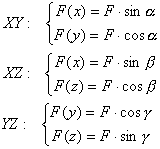 (1)
(1)
Таблица 3 – Величин углов векторов сил (в
Градусах)
|
Номер мышцы |
Угол α |
Угол β |
Угол γ |
|
1 |
-111,3 |
30,3 |
56,4 |
|
2 |
-84,33 |
14,32 |
50,1 |
|
3 |
-90 |
22,3 |
45,67 |
|
4 |
-60,3 |
65,17 |
64,7 |
|
5 |
-61 |
137,8 |
130,1 |
|
6 |
-61,4 |
123,3 |
124,41 |
|
7 |
81,85 |
23.5 |
57,21 |
|
8 |
80,3 |
46,6 |
48,73 |
|
9 |
43,15 |
20,03 |
87,5 |
|
10 |
-63,1 |
-71,5 |
47,5 |
|
11 |
-61,01 |
-81,6 |
49,1 |
|
12 |
-60,45 |
-145,27 |
40,35 |
|
13 |
-62,3 |
22 |
-34,65 |
|
14 |
-64,4 |
71,28 |
-90 |
|
15 |
-63,43 |
143,33 |
-95,6 |
|
16 |
61,01 |
160,72 |
-87,34 |
|
17 |
167,4 |
90,45 |
53,59 |
|
18 |
-60,78 |
180 |
-78,5 |
|
19 |
24,86 |
87,56 |
-34,35 |
|
20 |
-60,87 |
-67,5 |
-25,65 |
|
21 |
-61,43 |
-69,15 |
-31,2 |
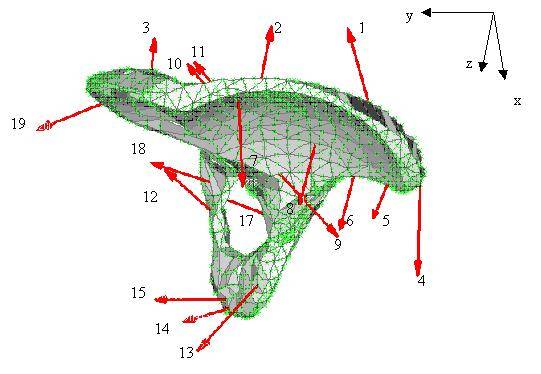
Рис. 2. Схема действий сил со стороны мышц
-
на основе полученных проекций векторов и метода сведения
этих векторов к общей точке строим для каждой из фаз суммарный вектор сил F(c),
по следующей формуле
![]() (2)
(2)
-
аналогичным путем рассчитываются проекции векторов F(б) гравитационных сил
оказываемых со стороны бедренной кости в области вертлужной впадины
тазобедренного сустава
Построение векторов нагрузки, действующих со стороны гравитационных сил,
осуществляется на основе представления человеческого тела в виде механической
системы - манипулятора. Для автоматизированного кинематического и динамического
анализа механизмов на ЭВМ необходимо кодирование параметров, описывающих
структуру, геометрию и распределение масс такой системы. Для описания такой
структуры весьма удобным и универсальным является метод графов, основанный на
понятии структуры дерева. Моделирования динамики манипуляторов связано с
необходимостью вычисления производных от кинетической энергии, что может внести
некоторые ошибки. Для того чтобы их избежать и разработать более эффективный
алгоритм автоматизированного анализа были использованы уравнения Лагранжа. В
данной работе применяем уравнения Лагранжа II рода, которые наиболее удобны как
при описании динамики объектов подобных рассматриваемому, так и при
программировании для ЭВМ.
Результаты моделирования
В результате моделирования, рассматриваемых фаз ходьбы, с помощью
программного продукта Matlab были получены следующие значения векторов силы мышц
и их проекций на соответствующие оси координат (таблица 4).
Таблица 4 – Величины сил мышц таза (в
Ньютонах)
|
№ Фазы |
F(x) |
F(y) |
F(z) |
F(c) |
|
1 |
-2492,127408 |
-844,037884 |
322,392705 |
2650,855715 |
|
2 |
-2012,613359 |
-1166,482438 |
-60,05330196 |
2326,993814 |
|
3 |
-2266,430441 |
-350,317541 |
623,2701986 |
2376,530047 |
|
4 |
-2291,267916 |
-485,6759863 |
491,7716651 |
2393,246581 |
|
5 |
-2141,454964 |
-798,0041572 |
170,2194172 |
2291,640165 |
|
6 |
-1415,28088 |
-1400,964088 |
-226,7070334 |
2004,274539 |
|
7 |
-253,1683385 |
-376,1882162 |
178,0131399 |
487,1349501 |
|
8 |
-1229,871223 |
-1187,35975 |
231,9483259 |
1725,168521 |
Со стороны головки бедренной кости также приложены силы, обусловленные действием,
как мышц бедра, так и весом человека. Величины этих сил, разложенные по фазам,
представлены в таблице 5.
Таблица 5 – Величины сил со стороны головки
бедренной кости (в Ньютонах)
|
№ Фазы |
F(x) |
F(y) |
F(z) |
F(б) |
|
1 |
-0,5 |
132,5 |
-587 |
601,7686433 |
|
2 |
573,05 |
310,66 |
-2244,38 |
2337,121632 |
|
3 |
239,01 |
252,14 |
-1861,43 |
1893,573871 |
|
4 |
51,27 |
89,21 |
-1541,92 |
1545,349256 |
|
5 |
75,11 |
345,41 |
-1239,53 |
1288,946935 |
|
6 |
-9,7 |
271,81 |
-567,88 |
629,6526507 |
|
7 |
9,1 |
140,63 |
-353,38 |
380,4432038 |
|
8 |
-10 |
103 |
-566,5 |
575,8743353 |
В результате приведения векторов к общей точке, расположенной в
суставном углублении тазобедренного сустава, получим обобщенный вектор сил, учитывающий
действие мышц и веса человека.
Таблица 6 – Величины обобщенных сил (в
Ньютонах)
|
№ Фазы |
F(x) |
F(y) |
F(z) |
F(o) |
|
1 |
-2492,627408 |
-711,537884 |
-264,607295 |
2605,66586 |
|
2 |
-1439,563359 |
-855,8224385 |
-2304,433302 |
2848,716826 |
|
3 |
-2027,420441 |
-98,17754099 |
-1238,159801 |
2377,627424 |
|
4 |
-2239,997916 |
-396,4659863 |
-1050,148335 |
2505,511419 |
|
5 |
-2066,344964 |
-452,5941572 |
-1069,310583 |
2370,242203 |
|
6 |
-1424,98088 |
-1129,154088 |
-794,5870334 |
1984,169352 |
|
7 |
-244,0683385 |
-235,5582162 |
-175,3668601 |
381,851493 |
|
8 |
-1239,871223 |
-1084,35975 |
-334,5516741 |
1680,785988 |
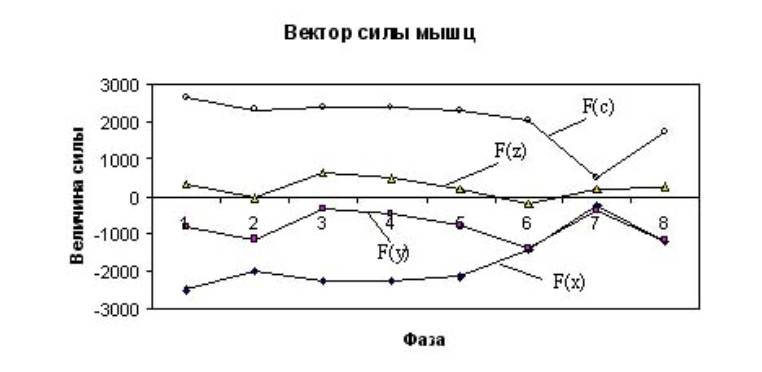
Визуальное представление изменение действия вектора силы и его проекций
на выбранную систему координат имеет следующий
вид:
Рис. 3. Диаграммы действующих сил со стороны мышц
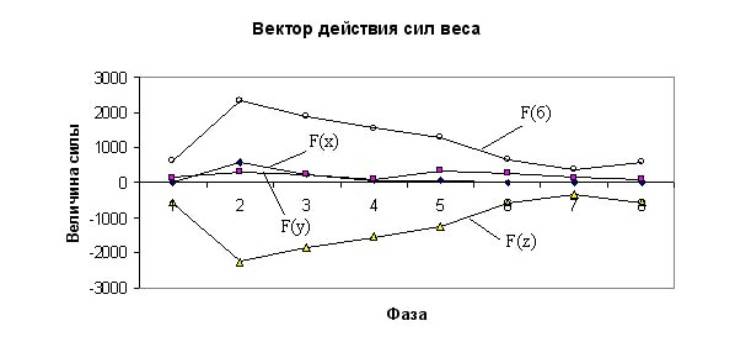
Рис. 4. Диаграммы действующих сил веса человека
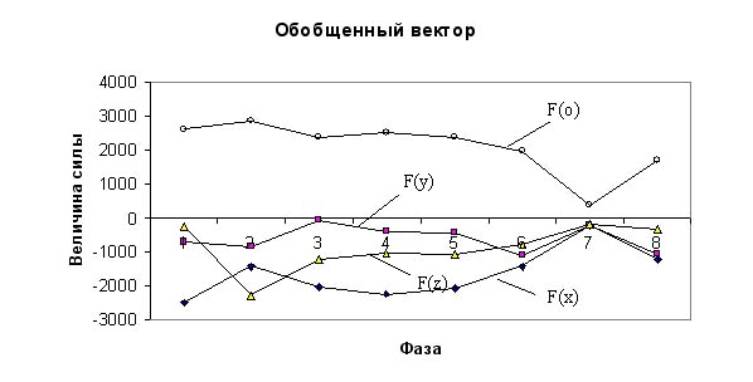
Рис. 5. Диаграммы обобщенного вектора сил
На рисунке 6 представлены трехмерные модели левой тазовой кости тазового
кольца и обобщенные фазовые вектора сил, действующих со стороны мышц и веса
человека при ходьбе.
Заключение
Основные выводы, вытекающие из анализа результатов взаимодействия тяги
мышц и гравитационных сил в области тазобедренного сустава, следующие:
- на основе численного эксперимента, методом аппроксимации по фазам был
выделен обобщенный вектор тяги со стороны мышц тазового кольца и вектор
действия гравитационных сил со стороны головки бедренной кости;
- на основе полученных векторов был рассчитан обобщенный вектор силы,
действующий на левую тазовую кость (правая тазовой кость является симметричной
и соответственно величины всех векторов останутся прежними, измениться лишь их
направление по оси X);
- полученные направления векторов совпадают с направлениями основных
линий напряжений в тазовом кольце при положении стоя, что говорит о достоверности
полученных данных [3].
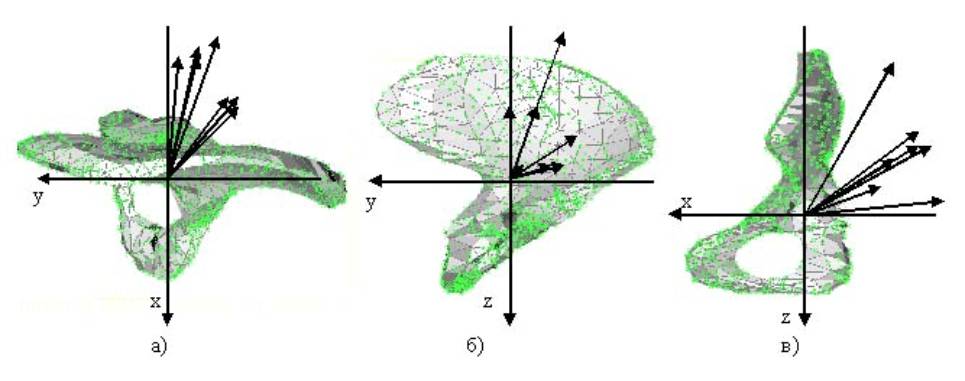
Рис. 6. Проекции трехмерной модели тазовой кости и обобщенных векторов
сил
Дальнейшее использование полученных данных предполагает выделение из
обобщенного вектора отдельных векторов сил, действующих в тех или иных отломках
подвздошной кости в зависимости от вида перелома. Данная информация позволит
учитывать влияние не только силы, действующие на костную ткань со стороны веса,
но и силы тяги мышц, при расчете максимальных нагрузок оказывающих своё влияние
на фиксирующее устройство.
ЛИТЕРАТУРА
1.
Бушманов
А. В., Назаренко Н. В., Серов М. А. Разработка компьютерной модели тазового
кольца // Математические методы в технике и технологиях ММТТ - 14: Сб. науч.
тр./ Смоленск: 2001. - Т.5. - Секция 7,8. - 47-48 с.
2. Crowninshield, R. D. and Brand, R. A. (1981) A physiologically based
criterion of muscle force prediction in locomotion. J. Biomechanics 14,
793-801.
3. Ekkehard Euler, Sandro-Michael Heining (2000) Anatomie und Biomechanik
des Beckens. Springer-Verlag 2000, Trauma und Berufskrankheit 2000 - 2, 2-10.
Calculation of loading in the pelvis ring’s region
Serov M. A.*, Rodionov A. A., Shatokhin N. V.**
In activity the interplay of
thrust forces is analyzed on the part of muscles of an ileal bone of a pelvic
ring and pressure in the field of a hip joint during walking. At realization of
biomechanical researches the 3D-model of an ileal bone was applied and the
programmatic complex MSC Nastran for Windows v4.0 was used.
Key words: Pelvic ring, three-dimensional model,
muscular fabrics, gravitation power, biomechanics, modeling.
*Институт геологии и
природопользования ДВО РАН, Благовещенск (smaik@ascnet.ru)
**Амурская государственная
медицинская академия, Благовещенск (shatohin78@mail.ru)
Поступила в редакцию
21.12.2006.