УДК [611.13/.16+611.423]: 616-006-092.9

ПРОВЕРКА ЗАКОНА МАРРЕЯ ДЛЯ МИКРОСОСУДИСТЫХ СЕТЕЙ

(smorodinov.doc)

Ó 2006 г. Бачерикова А. Г., Прудников И. М., Смородинов А. В.

В статье проводится проверка закона Маррея для микрососудистых сетей. Показано, что критерий оптимальности Маррея не функционирует в микрососудистых бифуркациях с диаметрами порядка 10÷50 мкм.

ВВЕДЕНИЕ

Одним из наиболее продуктивных направлений в исследовании гемомикрососудистых сетей связано с использованием в изучении законов построения этого отдела сердечно-сосудистой системы принципа оптимальности. Одной из первых оценочных функций, описывавших оптимальное построение гемомикрососудистых сетей, была предложена W. R. Hess (1914)[6]:

,

где – мощность, теряемая в результате вязкой диссипации; – потери мощности, связанные с теплоотдачей в окружающую среду и обусловленные наличием системы кровообращения. Различные оценочные функции критерия оптимальности функционирования системы кровообращения, предлагались разными авторами: Маррей (критерий минимизации энергии), A. Kamiya, T. Togowa (критерий минимизации объемного кровотока, с дополнительным условием, фиксирующим сопротивление сосудистой системы), Ф. Л. Черноусько (критерий минимума гемодинамического сопротивления с дополнительным условием, фиксирующим объем сосудистой системы), В. А. Глотовым и др.

Начало математическому моделированию сосудистых бифуркаций с точки зрения принципов оптимальности положили работы английского физиолога Маррея [10,11]. В своей первой работе [10] Маррей, используя принцип минимальной работы, описал диаметры кровеносных сосудов, а затем использовал полученные результаты для описания оптимального угла ветвления в своей второй работе [11]. Критерием оптимальности в модели Маррея является принцип минимизации энергии при прохождении постоянного (ламинарного) тока крови, с постоянной вязкостью через определенный сегмент артерии. Он показал, что энергия, затрачиваемая кровью при прохождении крови через сегмент артерии, описывается следующим уравнением:

, (1)

где P – падение давления; ƒ – значение кровяного потока (принимается как константа, при ламинарном течении); Vol – величина потока; r – радиус артерии; η – вязкость (константа). При постоянном ламинарном потоке крови ƒ на постоянной по протяженности участка артерии l энергия расхода минимальна, когда:

, (2)

подставляя уравнение (2) в уравнение (1) можно получить уравнение:

, (3)

или перенеся постоянные величины получить:

, (4)

Уравнение (4) использовалось для разработки теоретического закона угла ветвления в артериях, в соответствии с принципом минимизации работы. В общем случае, разветвление оптимально, если угол разветвления описывается формулой:

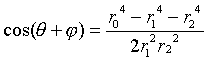, (5)

где - оптимальная величина угла разветвления в сосудистой бифуркации; - радиус просвета материнского ствола; , - радиусы просвета дочерних ветвей; и – углы отклонения ветвей от направления основного ствола.

В общем случае, при маркировке диаметров и углов отхождения микрососудов так, как показано на Рис. 1, параметры сосудов в точке бифуркации будут подчиняться следующей системе уравнений в модификации Глотова В. А. [2]:

d₃⁴-d₁⁴-d₂⁴-2d₁²d₂²cos j₁=0,

d₁⁴-d₂⁴-d₃⁴-2d₂²d₃²cos j₂=0, (6)

d₂⁴-d₁⁴-d₃⁴-2d₁²d₃²cos j₃=0,

где di – диаметры сосудов, ji – углы между сосудами, как показано на рисунке 1, iÎ1:3.

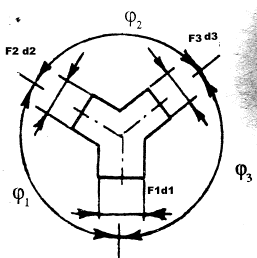
Рис. 1

Уравнения (6) есть запись закона косинусов для треугольника со сторонами ½Fi½, iÎ1:3, где Fi – силы, действующие на квант крови^* в каждом сосуде (Рис.1). Так, если кровь движется снизу вверх, то квант крови в первом сосуде в точке бифуркации делится на два кванта крови, продолжающие свои движения по сосудам 2 и 3. Поскольку система замкнутая, то по закону Ньютона имеем векторное уравнение для этих сил (Рис. 2)

F₁=F₂+F₃.

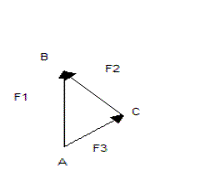
Рис.2.

Углы между сторонами треугольника равны соответственно:

Ð BAC=p-j₃, Ð ACB=p-j₂, Ð ABC=p-j₁.

Применяя теорему косинусов для каждой стороны треугольника ABC, получим три уравнения:

½AB½²=½BC½²+½AC½²-2½BC½½AC½cos(p-j₂)=½BC½²+½AC½²+ +2½BC½½AC½cos j₂ ,

½BC½²=½AB½²+½AC½²-2½AB½½AC½cos(p-j₃)=½AB½²+½AC½²+ +2½AB½½AC½cos j₃ ,

½AC½²=½AB½²+½BC½²-2½AB½½BC½cos(p-j₁)=½AB½²+½BC½²+ +2½AB½½BC½cos j₁ .

Стороны треугольника ABC равны длинам ½Fi½, iÎ1:3, которые в свою очередь равны по закону Паскаля произведению давления Pi, iÎ1:3, в каждом сосуде соответственно индексу на площадь его сечения Si, iÎ1:3, т.е.

½F_i½= P_i S_i ,

где

S_i=(pd_i²)/4

для iÎ1:3. Если давления во всех сосудах рассматриваемой бифуркации одинаковы, т.е. Pi=P, iÎ1:3, что справедливо для ламинарного потока, то, сокращая на P, получим уравнения Маррея.

МАТЕРИАЛЫ И МЕТОДЫ

Для исследования использовались пленчатые препараты МС 28 человеческих плодов погибших в результате самопроизвольных выкидышей или гистеротомии по социальным показаниям, ТКД 100 ÷ 280 мм (кожа, надкостница длинных трубчатых костей, суставная капсула, твердая мозговая оболочка, париетальная плевра, перикард, париетальная брюшина, брыжейка тонкой кишки и др.), изготовленных самостоятельно и из коллекции микропрепаратов Глотова В. А.

Препараты изготовлялись ориентированными: маркировка включала в себя номер плода, место получение препарата, ткань.

Спустя 10 часов после выкидыша и констатации смерти, плод погружался в ванночку с водой, нагретой до температуры 360 C, где выдерживался в течение одного часа для разогрева. Затем у плода препарировалась грудная клетка, и обнажалось сердце. Через левый желудочек в аорту, а затем через правый желудочек в легочную артерию вводилась инъекционная игла с оливой на конце и фиксировалась там лигатурой. При помощи 20 миллилитрового шприца производилась наливка сосудистой системы плода раствором туши приготовленной по Шпаннеру: чёрная чертёжная тушь разводится в соотношении 1:3 раствором Рингера, 6-кратно фильтруется и 2 раза центрифугируется по 15 минут при частоте вращения центрифуги 3000 об/ мин. Качество и достаточность наливки определялись по усиливающемуся почернению кожи и внутренних органов плода. После окончания наливки на аорту, лёгочную артерию, верхнюю и нижнюю полые вены накладывались лигатуры. Плод фиксировался в слабом растворе формалина 1:9 по Блюму в течение 14 суток. После окончания фиксации плод промывался в холодной проточной воде в течение 5 часов.

Препаровка проводилась макроскопическим способом на препаровальном столике. Дальнейшая обработка проводилась по следующей схеме: промывка в проточной воде, дегидратация в батарее спиртов, просветление в растворе карбол-ксилола, заключение в канадский бальзам.

Измерения диаметров микрососудов проводились при помощи винтового окулярного микрометра МОВ-1-15Х, в комплекте со стандартным объект-микрометром. Измерения углов между осями микрососудов проводились при помощи способа прямого измерения угла, образующегося при ветвлении между двумя сосудами, и устройства для его реализации, сконструированного на основе винтового окулярного микрометра МОВ-1-15х [3]. Всего производилось не мене тридцати измерений диаметров микрососудов и их углов отхождения.

МЕТОДИКА ПРОВЕРКИ ЗАКОНА МАРРЕЯ

Было рассмотрено более 40 бифуркаций. Без ограничения общности будем считать, что истинные значения параметров di, ji, iÎ1:3, бифуркации с вероятностью 1 принадлежат отрезкам, образованным минимальными dimin, jimin и максимальными значениями dimax, jimax, iÎ1:3, полученными в результате экспериментов для каждой бифуркации. Все дальнейшие данные указаны в микронах (мкм) и в градусах.

Экспериментальные данные для первой из выбранных случайным образом бифуркаций представлены в таблице 1:

Таблица 1

Экспериментальные данные, полученные при обсчете случайным образом выбранной бифуркации

d2	d1	d3	j1	j2	j3
33,3296	37,3832	16,2144	89	125	154
31,9784	37,158	16,4396	75	122	158
34,6808	36,032	16,2144	85	123	149
33,3296	36,032	17,1152	78	125	155
33,3296	35,5816	16,2144	82	122	159
32,654	35,8068	16,2144	87	119	155
33,1044	35,1312	19,3672	87	123	156
32,4288	35,8068	20,268	83	120	156
32,2036	35,1312	21,8444	78	122	159
32,2036	35,5816	22,52	75	124	155
33,78	34,906	22,52	79	123	150
33,3296	36,2572	22,2948	80	126	153
33,3296	35,8068	22,2948	82	124	153
33,5548	34,906	22,52	85	121	153
32,8792	34,906	20,268	84	126	154
32,8792	36,4824	20,268	83	124	155
32,8792	36,7076	19,142	82	122	156
33,5548	35,3564	19,5924	80	126	154
33,78	35,5816	19,5924	80	123	156
33,78	36,032	19,8176	79	124	157
33,5548	36,032	19,5924	79	126	155
32,4288	35,8068	20,268	79	120	160
33,3296	36,032	14,8632	77	126	156
33,1044	37,158	15,764	80	127	157
33,1044	36,2572	15,764	79	126	155
32,4288	35,8068	19,142	79	125	157
32,2036	36,2572	17,3404	77	120	159
34,0052	36,2572	20,268	79	124	154
33,78	36,032	20,0428	90	116	161
34,0052	38,0588	16,89	90	123	156

Отсюда получаем следующие значения для максимальных и минимальных значений:

d1min	d1max	d2min	d2max	d3min	d3max
34,906	38,058	31,97	34,68	14,86	22,29

Проверяем первое уравнение Маррея (см. (6)). Так как

d_3max⁴-d_1min ⁴-d_2min ⁴<0,

то независимо от значения угла j1, который по данным эксперимента с вероятностью 1 принадлежит отрезку [jmin, jmax], где jmin =75^o, jmax=90^o , первое уравнение Маррея не выполняется с вероятностью 1 (т.к. cos j1 >0).

Экспериментальные данные для второй из выбранных случайным образом бифуркаций представлены в таблице 2:

Таблица 2

Экспериментальные данные, полученные при обсчете случайным образом выбранной бифуркации

d1	d2	D3	j1	j2	j3
24,0964	20,268	14,8632	135	116	114
24,3216	20,4932	17,7908	142	105	115
24,3216	20,268	17,1152	140	105	117
23,646	20,0428	17,1152	137	104	115
23,646	20,268	17,1152	139	104	118
24,0964	20,0428	16,4396	141	102	114
24,0964	19,8176	17,1152	138	107	115
24,3216	20,4932	16,4396	141	103	112
24,5468	19,8176	16,6648	139	108	114
24,5468	20,4932	16,2144	142	113	113
24,5468	20,268	17,5656	142	102	118
24,772	20,4932	15,0884	138	103	117
24,5468	20,7184	15,3136	140	100	120
24,5468	20,268	15,3136	137	104	118
24,3216	20,0428	15,764	141	100	117
24,5468	20,4932	15,3136	142	114	113
23,8712	20,268	15,764	140	105	116
23,646	20,0428	15,0884	140	103	116
24,0964	20,7184	17,7908	140	104	113
24,0964	20,9436	14,8632	140	104	112
23,8712	20,268	15,5388	143	100	117
24,0964	20,268	15,0884	143	102	117
24,3216	19,142	14,8632	140	104	117
24,3216	20,268	17,1152	140	102	117
24,3216	20,4932	17,1152	141	99	118
24,3216	20,7184	17,1152	144	100	117
24,0964	20,7184	16,6648	140	103	113
24,0964	20,4932	16,89	140	100	118
24,0964	20,4932	16,89	141	100	117
24,3216	20,268	17,3404	142	102	112

Отсюда, как легко видно, максимальные и минимальные значения равны:

d1min	d1max	d2min	d2max	d3min	d3max
23,646	24,546	19,142	20,94	14,86	17,79

Проверяем второе уравнение Маррея (см. (1)). Так как

d_1min⁴-d_2max ⁴-d_3max ⁴>0,

то независимо от значения угла j₂, который по данным эксперимента c вероятностью 1 принадлежит отрезку [j_2min, j_2max], где j_2min =99^o, j_2max=116^o, второе уравнение Маррея не выполняется с вероятностью 1(т.к. cos j₂ <0).

Действительно, для любых j₂ из отрезка [j_2min, j_2max]

d₁⁴-d₂ ⁴-d₃ ⁴-2d₂²d₃²cos j₂ ≥ d_1min⁴-d_2max ⁴-d_3max ⁴,

так как cos j₂ <0.

Экспериментальные данные для третьей из выбранных случайным образом бифуркаций представлены в таблице 3:

Таблица 3

Экспериментальные данные, полученные при обсчете случайным образом выбранной бифуркации

d1	d2	D3	j1	j2	j3
45,7156	43,2384	42,1124	146	124	89
46,8416	42,788	41,662	145	124	90
47,0668	43,0132	41,662	144	124	92
47,7424	43,0132	41,8872	144	120	89
46,6164	43,914	41,4368	145	124	93
47,5172	45,9408	41,8872	145	124	90
47,7424	43,6888	41,662	146	121	91
47,9676	45,7156	42,1124	145	124	88
48,1928	45,04	42,1124	146	123	92
45,9408	45,2652	41,8872	144	119	87
47,9676	45,04	42,1124	148	120	90
46,8416	44,8148	41,4368	146	119	91
46,6164	44,1392	41,8872	151	120	88
45,9408	40,536	41,8872	151	123	95
46,3912	40,536	41,662	146	123	89
47,0668	42,1124	41,662	146	121	91
46,6164	41,8872	41,8872	147	124	89
47,292	43,4636	42,1124	149	120	90
46,3912	42,1124	41,8872	148	124	88
45,04	43,2384	41,8872	149	125	88
47,292	44,1392	42,1124	149	124	90
47,5172	42,788	41,8872	148	122	90
45,4904	42,788	41,4368	147	123	90
45,9408	44,5896	42,3376	144	123	87
46,3912	42,788	42,1124	147	120	90
46,3912	43,6888	42,1124	147	123	90
46,3912	43,4636	41,8872	148	121	89
46,3912	42,3376	41,662	148	121	90
45,9408	45,04	42,1124	148	121	88
45,9408	45,7156	42,1124	147	125	88

Отсюда, как легко видно, максимальные и минимальные значения равны

d1min	d1max	d2min	d2max	d3min	D3max
45,04	47,96	40,53	45,94	41,43	42,33

Проверяем второе уравнение Маррея (см. (1)). Проверка здесь немного сложнее от предыдущих. В данном случае приходится учитывать границы изменения угла j₂. Отрезок [j_2min, j_2max] изменения угла j₂ имеет следующие значения (в градусах)

j2min	j2max
119	125

Поскольку cos j₂ <0 для всех значений из отрезка [j_2min, j_2max], то для нахождения минимума написанного ниже выражения берем минимальное значение ji_min=119^o.

Проверим, что минимум функции f(.,.):R²®R

f(d₂, d₃)= d_1min⁴-d₂ ⁴-d₃ ⁴ – 2 d₂² d₃² cos(119^o)

по d₂ и d₃ достигается для d₂=d_2max и d₃=d_3max.

Покажем, что функция ψ(.,.):R²→R

ψ (x,y)= a-x²-y²-2xy cos(119^о)

вогнутая (выпуклая вверх), где a – произвольная константа.

Для этого вычислим матрицу ψ ^¢¢(.,.)=Ѳ ψ (.,.) ее вторых смешанных производных:

1 cos(119^o)

Ѳ ψ (.,.) = (-2) .

cos(119^o) 1

Легко видно, что матрица Ѳ ψ (.,.) – отрицательно определенная. Действительно, так как главный минор первого порядка Δ₁₁=1>0 и главный минор второго порядка Δ₂₂=1-cos²(119^o)>0, то матрица

1 cos(119^o)

cos(119^o) 1

– положительно определенная. Итоговая матрица отличается от написанной множителем (-2). Поэтому итоговая матрица – отрицательно определенная.

Следовательно, функция ψ (.,.) - вогнутая во всем пространстве R². Свое максимальное значение она принимает там, где ее производные равны нулю, т.е.

ψ ¢_x(x,y)=0, ψ ¢_y(x,y)=0.

Вычисляя производные, которые равны

ψ ¢_x(x,y)=-2x-2y cos(119^o),

ψ ¢_y(x,y)=-2y-2x cos(119^o),

и приравнивая их нулю, убеждаемся, что точка максимума – это начало координат, т.е. x=0,y=0.

Так как для x= d₂², y= d₃² функция ψ(x,y) = f(d₂, d₃), то сказанное о функции ψ(.,.) верно и для функции f(.,.). Отсюда и из вогнутости функции f(.,.) следует, что f(.,.) принимает свое минимальное значение по d₂Î[d_2min,d_2max],

d₃Î [d_3min,d_3max] при d₂= d_2max и d₃= d_3max. Нетрудно проверить, что

d_1min⁴-d_2max ⁴-d_3max ⁴ –2 d_2max² d_3max² cos(119^o) >0.

Второе уравнение Маррея не выполняется с вероятностью 1, так как для любых j₂ из отрезка [j_2min, j_2max] верно cos j₂ <0 и

d₁⁴-d₂⁴-d₃⁴-2d₂²d₃²cos j₂≥ d_1min⁴-d_2max ⁴-d_3max ⁴ –2 d_2max² d_3max² cos(119^o)>0.

Экспериментальные данные для четвертой из выбранных случайным образом бифуркаций представлены в таблице 4:

Таблица 4

Экспериментальные данные, полученные при обсчете случайным образом выбранной бифуркации

d1	d2	D3	φ1	φ2	φ3
28,15	27,2492	20,0428	102	110	140
29,9516	27,024	19,5924	105	107	143
28,8256	27,6996	18,4664	106	110	140
29,7264	27,6996	18,016	114	105	144
29,7264	27,4744	18,4664	115	105	144
29,0508	27,2492	20,7184	115	102	142
29,5012	27,2492	20,268	114	93	143
29,276	26,5736	20,268	112	101	143
30,1768	27,6996	22,52	117	100	142
27,024	27,6996	21,394	115	99	142
27,4744	27,4744	21,394	114	104	139
27,2492	27,9248	22,0696	116	104	139
27,4744	27,6996	25,2224	114	103	142
27,024	27,9248	26,3484	117	100	142
27,4744	27,6996	25,6728	115	102	144
27,2492	27,4744	22,52	114	103	142
27,4744	27,4744	22,52	116	99	142
27,4744	26,1232	22,52	115	103	143
27,2492	26,7988	22,52	115	103	143
27,2492	26,3484	19,8176	112	101	142
27,6996	26,5736	20,268	116	101	143
27,9248	26,1232	20,268	114	102	142
27,6996	26,1232	22,52	114	102	142
27,4744	26,3484	20,268	116	102	142
27,024	25,6728	23,1956	115	103	142
27,024	25,898	22,52	115	103	143
27,024	25,6728	22,52	115	101	141
26,3484	25,6728	22,0696	114	103	140
26,5736	25,4476	20,0428	115	102	142
26,5736	25,6728	20,0428	114	101	142

Отсюда получаем следующие значения для максимальных и минимальных значений:

d1min	d1max	d2min	d2max	d3min	D3max
26,348	30,17	25,44	27,92	18,01	26,34

Проверяем первое уравнение Маррея (см. (1)). Проверка здесь аналогична предыдущему случаю. В данном случае приходится учитывать границы изменения угла j₁. Отрезок [j_1min, j_1max] изменения угла j₁ имеет следующие значения (в градусах):

j1min	j1max
102	117

Поскольку cos j₁ <0 для всех значений из отрезка [j_1min, j_1max], то для нахождения максимума написанного ниже выражения берем максимальное значение j_1max=117^o.

Аналогично предыдущему случаю можно доказать, что функция f(.,.):R²®R

f(d₁, d₂)= d_3max⁴-d₁ ⁴-d₂ ⁴ – 2 d₁² d₂² cos(117^o)

вогнутая по d₁, d₂. Отсюда следует, что максимум функции f(.,.):R²®R

f(d₁, d₂)= d_3max⁴-d₁ ⁴-d₂ ⁴ – 2 d₁² d₂² cos(117^o)

по d₁ и d₂ достигается для d₁=d_1min и d₂=d_2min. Этот максимум равен –11495,22.

Поскольку максимум отрицательный, то с вероятностью 1 первое уравнение Маррея не выполняется.

Действительно, первое уравнение Маррея не выполняется с вероятностью 1, так как для любых j₁ из отрезка [j_1min, j_1max] верно cos j₁ < 0 и

d₃⁴-d₁⁴-d₂⁴-2d₁²d₂²cos j₁≤ d_3max⁴-d_1min ⁴-d_2min ⁴ – 2 d_1min² d_2min² cos(117^o)<0.

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Проверка осуществлялась для сосудов с диаметрами порядка 10-50 мкм. Измерения диаметров проводилось с некоторой ошибкой, распределенной, как показал тест, по закону, близкому с большой доверительной вероятностью (порядка 0,95) к нормальному.

Для проверки закона Маррея для сосудов с диаметрами 10-50 мкм случайным образом выбирались четыре бифуркации во всем указанном диапазоне измерения диаметров. Удалось доказать, что с вероятностью 1 хотя бы одно уравнение из трех уравнений закона Маррея не справедливо. Следовательно, основное предположение, сделанное при выводе уравнений Маррея, о ламинарном потоке крови для указанного диапазона диаметров также не справедливо. Так как характер движения крови главным образом зависит только от диаметров сосудов, то и для меньших диаметров отклонение от ламинарного потока будет только усиливаться.

Необходимо отметить, что модель Маррея построена на одном существенном допущении: поток крови в сосуде имеет ламинарный характер течения с постоянной динамической вязкостью. Иными словами, кровь оценивается как ньютоновская жидкость, для которой выполняется закон Пуазейля, также имеющий ряд ограничительных условий: жидкость однородна и ее вязкость постоянна; течение стационарно и не изменяется вдоль трубки; течение ламинарное; трубка жесткая; скорость жидкости на границе со стенкой равна нулю. Только последнее условие заведомо выполняется для кровеносных сосудов, а остальные, приближенно только для сосудов некоторых типов [7]. Такой характер течения крови может наблюдаться в крупных сосудах, но ни как не в микрососудах, где коэффициент динамической вязкости имеет сложную зависимость от напряжения сдвига. Феноменом, иллюстрирующим это, является эффект Фореуса-Линдквиста. Фореус и Линдквист измеряли кажущуюся вязкость крови в трубках различного диаметра (от 0,1 см до 10 мкм). Они проводили опыты при скоростях сдвига, достаточно высоких для того, чтобы не образовывались монетные столбики, и вязкость не зависела от скоростей сдвига. Оказалось, что при уменьшении диаметра трубок уменьшается кажущаяся вязкость. Из эффекта Фореуса-Линдквиста следует, что напряжение сдвига около стенки с уменьшением диаметра трубки снижается. В свою очередь, напряжение сдвига определяется как произведение скорости сдвига в жидкости, находящейся вблизи стенки, на местную вязкость жидкости. В движущейся суспензии частиц вязкость пристеночного слоя ниже. Но в то же время скорость сдвига в этом слое больше, а потому напряжение сдвига у стенки может увеличиваться. Таким образом, невозможно точно сказать, в какую сторону изменится напряжение сдвига у стенки [4]. Следовательно, пристеночный слой существенно влияет на течение крови в микрососудах, вызывая возникновение таких эффектов как эффект Фореуса (снижение показателя гематокрита), эффекты неравномерного распределения эритроцитов на разветвлениях (феномен сепарации, «скрининг эффект») а также уменьшение кажущейся вязкости крови (феномен Фореуса-Линдквиста) [7].

Известен также такой морфологический феномен как начальное искривление микрососудов в бифуркациях. Когда жидкость течет ламинарно по изогнутой части трубки, возникает изменение направления движения каждого элемента крови. При этом, возникает ускорение элементов, перпендикулярное направлению движения, как следствие, аксиальный слой, имеющий большее ускорение, будет стремиться к наружной стенке изгиба, а на смену ей придет жидкость из пристеночной области. Указанные перемещения слоев жидкости будут приводить к возникновению поперечной циркуляции («вторичное движение») [4]. При этом в зависимости от степени искривления микрососуда, будет меняться коэффициент динамической вязкости на концах этого микрососуда на входах в соседние микрососудистые бифуркации [8]. Помимо этого, известно, что деформируемость эритроцитов является одним из факторов, способных изменять вязкость крови. Показано, что всякое уменьшение эластичности эритроцита приводит к увеличению вязкости крови, которая в сложившейся ситуации перестает зависеть от скорости сдвига, и начинает вести себя как ньютоновская жидкость [9]. По всей видимости, именно в силу перечисленных обстоятельств, в литературе встречаются противоречивые данные при исследовании сосудов микроциркуляторного русла на критерий оптимальности по Маррею. Так при биомикроскопическом исследовании артериолярных бифуркаций Александрин А. А. и др. [1] выявили, что принцип оптимальности Маррея, функционирует в бифуркациях, начиная от 31 до 80 микрон, что идет в разрез с существовавшим мнением о том, что этот закон справедлив для сосудов с диаметром более 100 микрон. В свою очередь, Мамисашвили В. А. и др. [5], при изучении пиальных сосудов выявили, что геометрическая структура подсистемы крупных пиальных артерий (диаметром более 100 мкм) такова, что в них обеспечивается транспорт крови с минимальными энергетическими затратами, в соответствии с критерием оптимальности Маррея. В отличие от системы мелких пильных артерий (диаметром менее 100 мкм), в которых минимум расхода энергии не является критерием оптимального функционирования. Помимо всего прочего, исследования на тотальных препаратах сопряжены с рядом технических трудностей. Так, зачастую, при инъекционных методиках на препаратах выявляются конусовидные расширения в области бифуркаций, и как следствие, измерения диаметров просветов микрососудов не может ограничиваться единичными измерениями и должны представлять как минимум серию, позволяющую вывести определенную среднюю величину с известной ошибкой.

Очевидно, что использование модели, предложенной Марреем, с целью описания механизмов оптимального построения микрососудистого русла без введения дополнительных, учитывающих реологию крови в микроциркуляторном звене сердечно-сосудистой системы, представляется не оправданным. Более адекватными представляются модели, рассматривающие кровь как неньютонвскою жидкость.

Моделью, учитывающую вязкость крови, является модель Глотова В.А. [2], в соответствии с которой, конфигурация микрососудистого узла определяется законом сохранения импульса и моделью поведения крови как неньютоновской жидкости. Связь между оптимальной конфигурацией микрососудистого узла и гемодинамическим фактором описывается системой из трех уравнений:

Как видно из системы уравнений, в множители введен коэффициент динамической вязкости (). В случае, когда коэффициент вязкости одинаков во всех трех сосудах сосудистой бифуркации второе уравнение из модели Глотова В. А. будет идентично уравнению (5), предложенному Марреем. Это может свидетельствовать о том, что модель Маррея представляет собой лишь частный случай модели, предложенной Глотовым В. А.

ЛИТЕРАТУРА

1. Александрин В. В., Косилова Е. В., Александров П. Н. Соблюдение принципа оптимальности в микроциркуляторном русле мозга крыс // Бюл. эксперим. биологии и медицины. -1994. -№ 8.– С.134-135.

2. Глотов В. А. Структурный анализ микрососудистых бифуркаций. (Микрососудистый узел и гемодинамический фактор). - Смоленск: АО "Амипресс", 1995. – 255 с.

3. Рационализаторское предложение № 529 от 16.12.81. «Способ прямого измерения угла, образующегося при ветвлении между двумя сосудами МЦР и устройство для его реализации» Глотов В. А.

4. Каро К., Педли Т., Шротер Р., Сид У. Механика кровообращения. -М.: Мир, 1981. - С. 55-56. [Саго С. D., Pedley Т. J., Schroter R. С., Seed W. A. The mechanics of the circulation. - Oxford University Press. - New York. Toronto, I978].

5. Мамисашвили В. А., Бабунашвили М. К., Мчедлишвили Г. И. Критерий оптимального функционирования подсистем крупных и мелких пиальных артерий // Физиол. журн. -1975. -Т. 61. -№ 10. -С. 1501-1506.

6. Образцов И. В., Ханин М. А. Оптимальные биомеханические системы. -М.: Медицина, 1989. -272 с.

7. Ткаченко Б. И., Левтов В. А., Москаленко Ю. Е. Физиология кровообращения. Регуляция кровообращения. - Л.: Наука, 1986. - 639 с.

8. Фомин А. М. Конфигурация микрососудистых сетей и регуляция кровотока в миокарде. VII КОНГРЕСС МЕЖДУНАРОДНОЙ АССОЦИАЦИИ МОРФОЛОГОВ // Морфология.-2004. – Т. 126. -№4.

9. Чернух А. М., Александров П. Н., Алексеев О. В. Микроциркуляция,- М.: Медицина, 1984.- 429 с.

10. Murray C. D. The physiological principle of minimum work applied to the angle of branching of arteries// J. Gen. Physiology. -1926. -Vol. 9. -№ 6. -P. 835-841.

11. Murray C.D. The physiological principle of minimum work. I. The vascular system and the cost of blood volume// Proc. Natl. Acad. Sci. –1926. -№ 12. –S. 207-214.

* Термин “ квант крови” впервые введен д.м.н. Глотовым В. А. [2].

THE TESTING OF MURREY’S LOW FOR MICROVASCULAR NETWORKS

Bacherikova A. G., Prudnikov I. M., Smorodinov A. V.

In this article deals with testing of Murrey’s low for microvascular networks. It is shown that Murray’s criterion of optimality does not function in microvascular bifurcation with 10÷50 micromicron in diameter.

Кафедра анатомии человека

Смоленская государственная медицинская академия

Поступила в редакцию 17.06.2006.