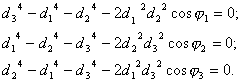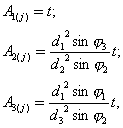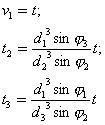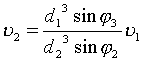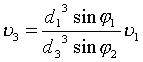На правах рукописи
СМОРОДИНОВ
Александр
Владимирович
МОДЕЛИРОВАНИЕ МИКРОСОСУДИСТОГО РУСЛА
(МОРФОЛОГИЧЕСКИЕ, БИОЛОГИЧЕСКИЕ, БИОФИЗИЧЕСКИЕ, МАТЕМАТИЧЕСКИЕ АСПЕКТЫ),
РАЗРАБОТКА СИНТЕТИЧЕСКОЙ МОДЕЛИ МИКРОСОСУДИСТЫХ СЕТЕЙ
14.00.02–
Анатомия человека
Автореферат
диссертации на
соискание ученой степени
кандидата
медицинских наук
Москва
2007
Официальные оппоненты:
Ведущая организация:
Защита состоится " "
2007 г. в часов на заседании диссертационного совета
С диссертацией в виде
автореферата можно ознакомиться
Диссертация в виде автореферата разослана
" "
Ученый секретарь диссертационного совета
ОБЩАЯ
ХАРАКТЕРИСТИКА РАБОТЫ
Актуальность
исследования
Система микроциркуляции
крови представляет собой одну из самых сложных циркуляторных систем природы,
развившуюся у многоклеточных организмов в процессе эволюции системы
кровообращения. Большое количество биологических, физических и химических
факторов влияет на архитектонику и топологию МС, а также на их
функционирование.
МЦР наибольшая по своей
протяженности часть сердечно-сосудистой системы. Общая длина микрососудов в
организме достигает астрономической величины порядка ![]() км. Количество микрососудов
в большом круге кровообращения составляет величину порядка
км. Количество микрососудов
в большом круге кровообращения составляет величину порядка ![]() , МУ -
, МУ - ![]() . Большая индиивидуальная изменчивость и пластичность МС
затрудняет процесс изучения этого морфологического объекта.
. Большая индиивидуальная изменчивость и пластичность МС
затрудняет процесс изучения этого морфологического объекта.
Исследование принципов и законов,
лежащих в основе построения и функционирования столь важного отдела
сердечно-сосудистой системы, является одним из важнейших направлений в
современной теоретической анатомии, основы которой были заложены П. Ф.
Лесгафтом. Это направление является ключом к пониманию как нормальных, так и
патологических процессов в МЦР.
Для понимания процессов,
определяющих конструкцию и функционирование МЦР, недостаточно одного
классического описательного метода. Одним из методов, позволяющих представить
структуру и поведение различных звеньев МС, является моделирование (морфологическое,
биологическое, биофизическое и математическое), которое при определенных
условиях с известной степенью достоверности может предсказывать поведение
моделируемого объекта.
В кажущемся хаосе конструкций
реальных МС существуют четкие закономерности, которые можно формализовать,
используя математический аппарат. Известны работы Roux W. (1878-1879), Murray
C. D. (1926), Krogh A. (1927), Thompson D'Arcy W. (1945), Cohn D. L.
(1954-1955), Розен Р. (1969), Kamiya A. M. D. (1972-2001), Zamir M.
(1973-2001), Мамисашвили В. А., Бабунашвили М. К., Мчедлишвили Г. И. (1972,
1974, 1975), Мелькумянца А. М. (1978), Шошенко К. А., Голубя А. С. (1975, 1977,
1978, 1982), Глотова В. А. (1986-2002), в которых предприняты попытки
разработать математические модели наблюдаемых морфологических феноменов в
конфигурации МС. Теоретические результаты, полученные этими авторами часто
не согласуются между собой и противоречат друг другу. В виду большой
трудоемкости и сложности экспериментальной проверки этих моделей, связанной с
методическими трудностями, в том числе и метрологическими, качественно и в
полном объеме ее провести до сих пор не удается, что значительно сдерживает
новые теоретические исследования топологии системы микроциркуляции.
Настоящее исследование является попыткой согласовать эти результаты между
собой, устранить противоречия между ними и показать пути их экспериментальной
проверки.
Цель
исследования
Изучение морфологических,
биологических, биофизических и математических аспектов конструкции
микрососудистого русла методами моделирования и разработка синтетической
модели МС.
Задачи
исследования:
1.
Провести
проверку модели C. D. Murray для МУ МС.
2.
Провести
проверку «закона кубов» для МУ МС и изучить соотношения диаметров микрососудов
в МУ МС.
3.
Разработать
модель, описывающую распределение скоростей потоков крови при прохождении через
МУ и провести ее экспериментальную проверку.
4.
Разработать
синтетическую модель МС.
5.
Изучить
ремоделирование МС в аутотрансплантате селезенки крысы.
6.
Изучить
при помощи БИМ распределение сосудистых сегментов в ткани селезенки крысы.
7.
Изучить
электрические явления в НОТ на коже человека и их связь с гемодинамикой в МС.
Научная новизна исследования
1.
Впервые
«закон кубов» рассматривается с позиции квантовой модели движения крови через
МУ.
2.
Выведена
система из трех уравнений, описывающая распределение скоростей потоков крови
при прохождении через МУ, представляющая собой развитие универсальной модели
оптимальной конфигурации МУ.
3.
Впервые
анализируется количество квантов крови, движущихся в микрососуде.
4.
Впервые
для анализа конфигурации МУ применена теорема Ферма, на основе которой получены
новые ограничения на разнообразие конфигураций МУ.
5.
Впервые
проведена проверка соотношений между величиной диаметров микрососудов в МУ на
основе предположения о средне арифметических соотношениях между ними.
6.
Впервые
для анализа МУ применяется теория вурфов.
7.
Разработана
синтетическая модель, в которой объединены основные морфологические,
биологические, биофизические и математические модели МС.
8.
По
данным БИМ установлено наличие, по крайней мере, 8 различных по своей
электропроводности зон в селезенки крысы.
9.
Показано,
что электрические явления в НОТ кожи человека не связаны с микроциркуляцией
крови.
Теоретическое значение исследования
Основное теоретическое значение исследования заключается в том, что оно показывает эффективность и плодотворность парциальной или квантовой модели движения крови через МУ, из которой следует универсальная модель оптимальной конфигурации МУ, развитие которой в свою очередь приводит к решению проблемы распределения скоростей при движении крови в микрососудах МУ.
Практическая
ценность исследования
Практическая ценность исследования заключается в том, что в процессе его выполнения были разработаны ряд новых устройств и методик, таких как устройство для качественного пропитывания биологического материала вакуумным методом, устройство для засвечивания биологического материала, электроды для измерения полного электрического сопротивления (импеданса) биологических тканей, переходное кольцо между бытовой цифровой видеокамерой Sony DCR-HC17E и микроскопом МББ–1, экспериментальная установка для электрохимического лизиса, способ определения полного электрического сопротивления (импеданса) биологических тканей, способ оценки соотношения красной и белой пульпы в гистологических препаратах селезенки, способ определения параметров микрососудистых бифуркаций при биомикроскопии
Основное
положение, выносимое на защиту
Парциальная или квантовая модель движения крови через МУ является фундаментальной основой для построения синтетической модели МС, которая позволяет объединить в единое целое комплекс описательных, экспериментальных и теоретических данных, полученных с использованием принципа оптимальности, универсальной модели оптимальной конфигурации МУ, универсального принципа симметрии П. Кюри, теоремы Ферма, теории вурфов, термодинамики и теории информации, теории фракталов, и теории графов.
Апробация
материалов исследования
Апробация материалов
исследования проведена на научных конференциях в виде докладов на: 27
Конференции молодых учёных и 51 научной студенческой конференции СГМА
(Смоленск, 14 апреля 1999 г.); 1 Международной студенческой конференции,
посвященной 40-летию СНО Гродненского медицинского университета (Гродно, 26-28
апреля 2000 г.); 28 Конференции молодых учёных и 52 научной студенческой
конференции СГМА (Смоленск, 27 апреля 2000 г.); 29 Конференции молодых учёных и
53 научной студенческой конференции СГМА (Смоленск, 26 апреля 2001 г.); 30
Конференции молодых учёных и 54 научной студенческой конференции СГМА
(Смоленск, 25 апреля 2002 г.); 32 Конференции молодых учёных и 56 научной студенческой
конференции СГМА (Смоленск, 22 апреля 2004 г.); заседании проблемной комиссии
Смоленской государственной медицинской академии (СГМА) по иммунологии,
иммуноморфологии и иммунопатофизиологии (Протокол от 24 ноября 2004 г.);
33 Конференции молодых учёных и 57 научной студенческой конференции СГМА
(Смоленск, 22 апреля 2004 г.); 34 Конференции молодых учёных и 58 научной
студенческой конференции СГМА (Смоленск, 27 апреля 2006 г.).
По материалам исследования
опубликовано 8 научных работ: научных статей - 3, тезисов докладов - 5; заявок
на изобретения - 3, рационализаторских предложений - 8.
Структура и
объем диссертации
Исследование выполнено на
кафедре анатомии человека и в центральной научно-исследовательской лаборатории
(ЦНИЛ) Смоленской государственной медицинской академии (СГМА) и относится к
области теоретической анатомии.
Исследование выполнено в
рамках НИР, включенных в государственный план СГМА [Протокол заседания ученого
совета №12 от 7 декабря 2004 г. Номер государственной регистрации НИР во ВНТИЦ - 01200502621].
Диссертация представлена в
виде рукописи объемом 183 с.; рисунки –42, таблицы – 19; библиография – 290
источников (отечественных – 222, зарубежных – 68).
Весь материал,
представленный в автореферате, получен, обработан и проанализирован лично
автором.
Содержание работы:
1.
Аббревиатуры,
Условные обозначения
2.
Введение
2.1.
Терминологический
аппарат
2.2.
Актуальность
исследования
2.3.
Материалы
и объект исследования
2.4.
Цель
и задачи исследования
2.5.
Основные
положения, выносимые на защиту
2.6.
Научная
новизна, теоретическое значение, практическая ценность исследования
2.7.
Общая
характеристика работы и апробация результатов
исследования
3.
Обзор
литературы
3.1.
Понятие
моделирования. Виды моделей, используемые для
моделирования архитектоники
микрососудистого русла и
гемодинамики
3.2.
Морфологические
аспекты моделирования микрососудистого
русла
3.3.
Биологические
аспекты моделирования микрососудистого русла
3.4.
Биофизические
аспекты моделирования микрососудистого русла
3.5.
Математические
аспекты моделирования микрососудистого русла
3.5.1.
Модели,
описывающие движение крови в микрососуде
3.5.2. Модели, описывающие движение
крови в микрососудистом
узле
3.5.3. Модели общей конфигурации
микрососудистых сетей
4.
методы
исследования
4.1.
Методика
выявления микрососудистых сетей в пленчатых
образованиях
человеческих плодов и их морфометрия
4.2.
Биомикроскопия
микрососудистых сетей плавательной перепонки задней лапки озерных лягушек
4.3.
Компьютерный
анализ микрососудистых сетей
4.4.
Исследование
ремоделирования микрососудистых сетей
на примере
аутотрансплантации фрагментов селезенки крысы в большой сальник
4.5.
Биоимпедансометрические
исследования микрососудистых сетей селезенки у крысы
4.6.
Исследование
низкоомных точек на коже человека
5.
Результаты
собственных исследований
5.1.
Проверка
модели C. D. Murray на пленчатых препаратах
микрососудистых сетей
париетальной плевры, твердой
мозговой оболочки, кожи,
мышечных фасций, суставной капсулы,
надкостницы длинных
трубчатых костей, надхрящницы,
перикарда, брыжейки тонкой
кишки человеческих плодов
5.2.
Проверка модели C. D. Murray при биомикроскопии
микрососудистых
сетей плавательной перепонки задней лапки озерных лягушек
5.3.
Проверка
«закона кубов» для микрососудистых узлов
5.4.
Развитие
универсальной модели оптимальной
конфигурации
микрососудистого узла
5.5.
Синтетическая
модель микрососудистых сетей
5.6.
Ремоделирование
микрососудистых сетей в аутотрансплантате
селезенки
крысы
5.7.
Биоимпедансометрические
исследования микрососудистых сетей селезенки крысы и электрических явлений в
низкоомных точках на коже человека
6.
ЗАКЛЮЧЕНИЕ
7.
Литература
Материалы
исследования
·
30
человеческих плодов ТКД 100÷280 мм (1÷6 лунных месяцев).
·
17
крыс линии Wistar.
·
10
озерных лягушек.
·
7
женщин в возрасте от 17 до 23 лет - контрольная группа.
·
27
человеческих трупов, из которых 13 женщин в возрасте от 5 до 74 лет и 14 мужчин
в возрасте от 28 до 80 лет.
Объект исследования
· МС и МУ (МБ) человеческих плодов
(париетальной плевры, твердой мозговой оболочки, кожи, мышечных фасций,
суставной капсулы, надкостницы длинных трубчатых костей, надхрящницы, перикарда,
брыжейки тонкой кишки). Общая площадь исследованных МС на тотальных
препаратах ![]()
![]() мм2. Общее
количество МУ
мм2. Общее
количество МУ ![]()
![]() .
.
· МС и МУ (МБ) плавательной
перепонки задней лапки озерных лягушек. Общая площадь исследованных МС при
биомикроскопии ![]()
![]() мм2. Общее
количество МУ -
мм2. Общее
количество МУ - ![]() .
.
· Селезенка крыс.
· БАТ (P11 «шао-шан», C9
«шао-чун» и C8 «шао-фу») на коже живых людей из
контрольной группы.
·
НОТ
(P11 «шао-шан», C9 «шао-чун» и C8 «шао-фу») на
коже трупа человека.
Методы
исследования
1.
Наливка
тушью МС пленчатых препаратов
человеческих плодов.
2.
Импрегнация
МС гистологических срезов аутотрансплантатов селезенки крысы азотнокислым
серебром по В. В. Куприянову.
3.
Окраска
гистологических срезов аутотрансплантатов селезенки крысы
гематоксилин-эозином.
4.
Морфометрия
МС (измерение диаметров микрососудов) при помощи винтового окулярного
микрометра МОВ-1-15Х.
5.
Измерения
углов между осями микрососудов в МУ при помощи способа прямого измерения
угла, образующегося при ветвлении между двумя сосудами, и устройства для его
реалиизации, сконструированного на основе винтового окулярного микрометра
МОВ-1-15х.
6.
Биомикроскопия
микрососудистых сетей плавательной перепонки задней лапки озерных лягушек с
видеорегистрацией и компьютерной обработкой изображений [Рационализаторское предложение № 1483 от 01.03.2006.
(Бриз СГМА)].
7. Компьютерный анализ
микрососудистых сетей при помощи графического редактора Adobe Photoshop v. 6.0,
редактора видеоизображений WinDVD Creator (лицензионная версия), с изготовлением
коротких видеороликов, содержащих один МУ, электронных таблиц MS Excel 2003
SP1 (лицензионная версия). Обработка стоп-кадров с применением оригинального
алгоритма определения параметров МУ (![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() ) при помощи циркуля, транспортира и школьной миллиметровой
линейки [Рационализаторское предложение
№1501 от 22.01.2007. (Бриз СГМА)], алгоритма проверки соответствия
диаметров «закону кубов»:
) при помощи циркуля, транспортира и школьной миллиметровой
линейки [Рационализаторское предложение
№1501 от 22.01.2007. (Бриз СГМА)], алгоритма проверки соответствия
диаметров «закону кубов»: ![]() ; алгоритма нахождения процентного отклонения отношения
значений между суммой кубов
; алгоритма нахождения процентного отклонения отношения
значений между суммой кубов ![]() ,
, ![]() и
и ![]() из выражения:
из выражения:
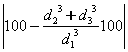 (%);
(%);
алгоритма проверки
оптимальности фактического угла ![]() в соответствии с
моделью оптимальности C. D. Murray, алгоритма расчета теоретического угла
в соответствии с
моделью оптимальности C. D. Murray, алгоритма расчета теоретического угла ![]() по экспериментальным
значениям диаметров осевых потоков:
по экспериментальным
значениям диаметров осевых потоков:
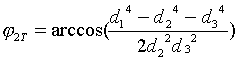 ;
;
алгоритма нахождение
процентного отклонения отношения значений теоретического угла ![]() к фактическому углу
к фактическому углу ![]() из выражения:
из выражения:
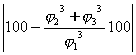 (%);
(%);
алгоритма
определения количества квантов крови в микрососуде:
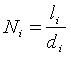 ,
,
где ![]() - предполагаемое
число квантов крови, движущихся в i-м
микрососуде,
- предполагаемое
число квантов крови, движущихся в i-м
микрососуде,
![]() - длина капилляра
между двумя соседними МУ,
- длина капилляра
между двумя соседними МУ,
![]() - среднее значение
диаметров;
- среднее значение
диаметров;
алгоритма определения
отношения линейных скоростей ![]() к
к ![]() в МУ по формуле:
в МУ по формуле:
|
|
8. Математическое
моделирование МС при помощи электронных таблиц MS Excel 2003 на основе
математических моделей C. D. Murray и В. А. Глотова, «закона кубов», теории
вурфов.
9. Статистическая обработка
осуществлялась методами, изложенными в общепринятых руководствах и при помощи
программы статистического анализа Statistica 6.0. (лицензионная версия).
10. Ремоделирование МС на
примере аутотрансплантации фрагментов селезенки крысы в большой сальник.
11. Биоимпедансометрия
селезенки у крысы при помощи оригинальной экспериментальной установки
исследования микрососудистых сетей селезенки у крысы [Рационализаторское
предложение № 1480 от 12.12.2005. (БРИЗ СГМА)] и оригинальных токопроводящих
электродов [Рационализаторское предложение 1482 от 02.02.2006. (Бриз СГМА),
Авторская справка 200613874604257 от 02.11.2006].
12. Исследование низкоомных
точек на коже человека при помощи прибора для электрорефлексотерапии ЛУЧ-1.
Все экспериментальные
исследования на животных и человеке проводились в соответствии с требованиями
Этического комитета СГМА.
РЕЗУЛЬТАТЫ
СОБСТВЕННЫХ ИССЛЕДОВАНИЙ И ИХ ОБСУЖДЕНИЕ
1.
Терминологический аппарат
Микрососуд – первый основной структурно-функциональный элемент
микрососудистых сетей (МС).
Микрососудистый
узел (МУ) [разветвление, бифуркация, ответвление, дихотомическое деление, микрососудистая
бифуркация (МБ), трифуркация, трихотомическое деление, сосудистый тройник,
мультифидное ветвление] – второй основной структурно-функциональный элемент микрососудистых
сетей (МС), представляет собой соединение или стык трех микрососудов в
области разветвления и прилегающие к ним их начальные участки.
Степень ветвления микрососудистого узла (МУ) n – число микрососудов
образующих МУ.
Универсальная биологическая константа ангиогенеза – степень ветвления
микрососудистого узла (МУ) n=3.
Микрососудистые сети (МС) – совокупность микрососудистых
узлов, соединенных между собой микрососудами.
Конфигурация микрососудистого узла (МУ) – конфигурация внутреннего
просвета микрососудистого узла.
Правила индексации параметров МУ (![]() ,
, ![]() , где i=1, 2, 3) – правила регламентирующие присвоение параметрам
, где i=1, 2, 3) – правила регламентирующие присвоение параметрам ![]() и
и ![]() индекса i.
индекса i.
Правила Ру (W. Roux) – правила регламентирующие отношение между параметрами ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() в МУ.
в МУ.
Принцип оптимальности для МС:
По Р. Розену (Rosen R.): «Природа выполняет свои задачи таким способом, которые являются в
некотором смысле наилучшим из всех возможных…».
По В. Ру (Roux W.) конфигурация артериальной бифуркации соответствует принципу
минимальных затрат энергии и материала («minimum lebendiger Kraft und Wandungsmaterial» - нем). Эмпирически установленные
правила В. Ру являются морфологическим выражением принципа минимальных затрат
энергии им материала для микрососудистых бифуркаций.
По Murray C. D. конфигурация сосудистой бифуркации оптимальна, если связь между величинами
углов разветвления ![]() ,
, ![]() ,
, ![]() и их диаметров
и их диаметров ![]() ,
, ![]() ,
, ![]() описывается моделью в
виде системы уравнений:
описывается моделью в
виде системы уравнений:
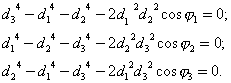
По В. А. Глотову – конфигурация
микрососудистой бифуркации оптимальна если связь между величинами полного давления крови H, коэффициента
динамической вязкости крови ![]() , углов разветвления
, углов разветвления ![]() ,
, ![]() ,
, ![]() и их диаметров
и их диаметров ![]() ,
, ![]() ,
, ![]() описывается моделью в
виде системы уравнений (универсальной модели оптимальной конфигурации
микрососудистого узла):
описывается моделью в
виде системы уравнений (универсальной модели оптимальной конфигурации
микрососудистого узла):
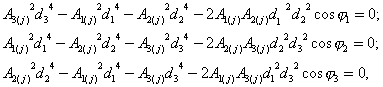
где j=1,2; при j=1, Ai(1)=Hi; при j=2, Ai(2)=![]() ;
;
Hi и ![]() – соответственно
полное давление крови и коэффициент динамической вязкости крови в
– соответственно
полное давление крови и коэффициент динамической вязкости крови в ![]() -м микрососуде;
-м микрососуде;
![]() – диаметр
– диаметр
![]() -го микрососуда (
-го микрососуда (![]() <100 мкм);
<100 мкм);
![]() – угол
между осями симметрии просветов микрососудов,
при этом
– угол
между осями симметрии просветов микрососудов,
при этом
0< ![]() <180°,
<180°, ![]() ;
; ![]() = 1,2,3.
= 1,2,3.
Частным случаем этой модели является модель Murray C. D. и соответственно эмпирические правила В. Ру.
Искривление микрососуда – искривление, изгиб поворот
микрососуда.
Пластичность микрососудистых сетей – способность микрососудистых
сетей изменять свою конфигурацию при изменениях параметров гемодинамики и при
этом вновь принимать оптимальную конфигурацию.
Универсальный принцип симметрии П. Кюри. В 1894 П. Кюри сформулировал
принцип симметрии: "При наложении нескольких явлений различной природы в
одной и той же системе их диссимметрии складываются. Элементами симметрии
системы остаются только те, которые являяются общими для каждого явления,
взятого отдельно. Когда некоторые действия проявляют некоторую диссимметрию,
то эта диссимметрия должна обнаруживаться и в причинах, их порождающих.
Положение, обратное этим двум, несправедливо, по крайней мере практически,
т.е. произведенные действия могут быть более симметричными, чем причины".
Энантиоморфизм - свойство некоторых веществ кристаллизоваться в
"левой" и "правой" модификациях.
Энантиоморфизм
МС – свойство микрососудистых сетей развиваться в «левой» и «правой»
модификациях в зависимости от положения соответственно в левой или правой
половине тела.
Гемодинамический фактор – физическое воздействие на
сосудистую стенку потока крови, движущегося в системе сосудов.
Квант крови (порция крови) – движение крови по сосудам
можно представить как непрерывный поток объемов жидкости, следующих друг за
другом вплотную, без разрывов.
Парциальная или квантовая модель движения крови через МУ. Движение крови по сосудам
можно представить в виде непрерывного потока квантов крови. При продвижении
через МУ квант крови либо распадается на два новых кванта, либо сливается с
другим квантом, с образованием нового.
Гипотеза о сверхтекучести крови – предположение о том, что
сосудистая стенка микрососудистого узла при оптимальной конфигурации его просвета
не оказывает практически значимого сопротивления движению крови. При
прохождении через МУ, имеющий оптимальную конфигурацию просвета, кровь
приобретает свойство «сверхтекучести крови», т.е. движение крови происходит
без практически значимой потери энергии.
«Закон кубов» для микрососудистого узла (МУ) оптимальной
конфигурации:
![]() .
.
Число
квантов крови N – число квантов крови, движущихся в микрососуде между
двумя соседними МУ. Число N всегда целое, т.е. принадлежит к множеству натуральных
чисел.
Ограничения многообразия конфигураций МУ, регламентированные
теоремой Ферма. Теорема Ферма накладывает ограничения на конфигурацию МУ, сущность
которого заключается в том, что параметры ![]() ,
, ![]() ,
, ![]() не могут одновременно
быть целыми числами, т.е. относиться к множеству натуральных чисел.
не могут одновременно
быть целыми числами, т.е. относиться к множеству натуральных чисел.
Модель количественных отношений между
значениями ![]() ,
, ![]() ,
, ![]() в МУ:
в МУ:
При условии
![]() >
>![]() >
>![]() ,
,
![]() ,
,
При
условии ![]() >
>![]() >
>![]() ,
,
![]() ,
,
W – вурф или двойное отношение четырех точек
A,B,C,D одной прямой,
которое вычисляется по формуле Петухова С. В.:
W=(C-A)(D-B)/(C-B)(D-A).
В живой природе реализуется общий принцип
построения биологических тел из конформно-симметричных блоков. Симметрии
биологических тел во многих случаях демонстрируют связь с рядом Фибоначчи.
Три соседних числа ряда Фибоначчи могут быть интерпретированы как длины трех
последовательных отрезков, заключенных согласно рекурентному ряду Фибоначчи
между четырьмя точками. Величина вурфов всех последовательных троек точек
чисел Фибоначчи образуют новую – вурфовую – последовательность. Предельная
величина (1,309) вурфовой последовательности называется золотым вурфом.
2. Проверка
модели C. D. Murray на пленчатых препаратах микрососудистых сетей париетальной
плевры, твердой мозговой оболочки, кожи, мышечных фасций, суставной капсулы,
надкостницы длинных трубчатых костей, надхрящницы, перикарда, брыжейки тонкой
кишки человеческих плодов
Анализировалась
рандомизированная выборка из 40 МУ, для которых определялись параметры ![]() ,
, ![]() . На рандомизированной выборке из 4-х МУ проверялась модель C. D. Murray.
Удалось доказать, что с вероятностью 1 хотя бы одно уравнение из трех уравнений
C. D. Murray несправедливо для МУ с диаметрами микрососудов 50 мкм и меньше.
. На рандомизированной выборке из 4-х МУ проверялась модель C. D. Murray.
Удалось доказать, что с вероятностью 1 хотя бы одно уравнение из трех уравнений
C. D. Murray несправедливо для МУ с диаметрами микрососудов 50 мкм и меньше.
Вторым подходом к анализу
справедливости модели C. D. Murray является расчет процентного отклонения
значения j2т от j2ф. в исследованных 40 МУ.
Используя методику расчета процентного отклонения значений j2т от j2ф (2-е
уравнение из модели C. D. Murray), удалось выявить, что
большая часть значений процентного отклонения
j2т от j2ф находится в области значений 155 процентов. Из этого следует,
что в большинстве случаев расчетное j2т отличается от j2ф более чем в полтора раза, что позволяет предположить, что
модель C. D. Murray, не отражает реальную
конфигурацию исследованных МУ.
3. Проверка
модели C. D. Murray при биомикроскопии МС
плавательной перепонки задней лапки озерных лягушек
Анализировалась
рандомизированная выборка из 100 МУ, для которых определялись параметры ![]() ,
, ![]() . Величина процентного отклонения значений j2т от j2ф во 2-м уравнении модели C.
D. Murray колебалась в широких пределах
от 1,5% до 721%. В 31 МУ расчет j2т по экспериментальным значениям
диаметров был невозможен, в связи с тем, что косинус угла j2ф принимал значение больше 1.
В оставшихся 69 МУ процент отклонения не превышал 104%. В интервале отклонения
от 0% до 60% характер распределения приближался к нормальному типу. Это
свидетельствует, что процент отклонения значений j2т от j2ф в этом интервале носит случайный характер, что указывает на то,
что модель C. D. Murray не отражает конфигурации МУ в исследованных МС.
. Величина процентного отклонения значений j2т от j2ф во 2-м уравнении модели C.
D. Murray колебалась в широких пределах
от 1,5% до 721%. В 31 МУ расчет j2т по экспериментальным значениям
диаметров был невозможен, в связи с тем, что косинус угла j2ф принимал значение больше 1.
В оставшихся 69 МУ процент отклонения не превышал 104%. В интервале отклонения
от 0% до 60% характер распределения приближался к нормальному типу. Это
свидетельствует, что процент отклонения значений j2т от j2ф в этом интервале носит случайный характер, что указывает на то,
что модель C. D. Murray не отражает конфигурации МУ в исследованных МС.
4. Проверка
«закона кубов» для МУ
Анализ процентного
отклонения значений между суммой кубов ![]() ,
, ![]() и
и ![]() в 40 МУ МС
париетальной плевры, твердой мозговой оболочки, кожи, мышечных фасций,
суставной капсулы, надкостницы длинных трубчатых костей, надхрящницы, перикарда,
брыжейки тонкой кишки человеческих плодов, показал, что величина этого
отклонения варьирует в широких пределах (10÷66%), ее распределение
приближается к нормальному, что указывает на то, что в исследованных МС «закон
кубов» не выполняется. Это связано с тем, что в «мертвых» МС отсутствует
гемодинамический фактор и его динамическое формообразующее влияние; в
результате наливки ригидных МС тушью при неконтролируемом давлении и
гистологической обработки происходят деформации просветов микрососудов.
«Мертвые» МС непригодны для проверки «закона кубов».
в 40 МУ МС
париетальной плевры, твердой мозговой оболочки, кожи, мышечных фасций,
суставной капсулы, надкостницы длинных трубчатых костей, надхрящницы, перикарда,
брыжейки тонкой кишки человеческих плодов, показал, что величина этого
отклонения варьирует в широких пределах (10÷66%), ее распределение
приближается к нормальному, что указывает на то, что в исследованных МС «закон
кубов» не выполняется. Это связано с тем, что в «мертвых» МС отсутствует
гемодинамический фактор и его динамическое формообразующее влияние; в
результате наливки ригидных МС тушью при неконтролируемом давлении и
гистологической обработки происходят деформации просветов микрососудов.
«Мертвые» МС непригодны для проверки «закона кубов».
При анализе 100 МУ,
полученных при биомикроскопии МС плавательной перепонки задней лапки озерных
лягушек, большая часть отклонений значений между суммой кубов ![]() ,
, ![]() и
и ![]() группируется вокруг
величины, равной 15%. При анализе распределения процентного отклонения в исследуемой
статистической совокупности МУ с помощью критерия χ2 было установлено несоответствие этого распределения
нормальному, что можно интерпретировать в пользу справедливости «закона
кубов» в исследованных МС, что соответствует литературным данным.
группируется вокруг
величины, равной 15%. При анализе распределения процентного отклонения в исследуемой
статистической совокупности МУ с помощью критерия χ2 было установлено несоответствие этого распределения
нормальному, что можно интерпретировать в пользу справедливости «закона
кубов» в исследованных МС, что соответствует литературным данным.
Получен парадоксальный результат: модель C. D. Murray не отражает конфигурации МУ, образованных
микрососудами, имеющими диаметр внутреннего просвета менее 100 мкм, и
справедлива для МУ, образованных микрососудами и сосудами, имеющими диаметр
внутреннего просвета более 100 мкм; «закон кубов» выполняется как в первом
случае, так и во втором. Можно сделать заключение, что «закон кубов» обусловлен
действием общих физических законов: закона неразрывности струи или потока,
закона сохранения вещества.
5. Развитие
универсальной модели оптимальной конфигурации МУ
Модель C. D. Murray является
частным случаем универсальной модели оптимальной конфигурации МУ, при условии
поведения крови как ньютоновской жидкости. Более общей моделью является
универсальная модель оптимальной конфигурации МУ, предложенная Глотовым В. А.
в 1995 г., которая рассматривает кровь, движущуюся в МС, как неньютоновскую
жидкость. Из универсальной модели оптимальной конфигурации МУ, созданной на
основе парциальной или квантовой модели движения крови через МУ, учитывая, что
квант крови под действием сил поверхностного натяжения крови стремится принять
форму шара, что обуславливает соотношение ![]() , где
, где ![]() - длина кванта крови,
можно получить выражения, описывающие распределение скоростей потоков
крови при прохождении через МУ.
- длина кванта крови,
можно получить выражения, описывающие распределение скоростей потоков
крови при прохождении через МУ.
|
|
Данная система уравнений
имеет континуум решений относительно параметров ![]() ,
, ![]() ,
, ![]() :
:
|
|
Проверка отношений скоростей
![]() к
к ![]() :
:
|
|
на рандомизированных 6-и МУ МС плавательной
перепонки задней лапки озерных лягушек показала их соответствие
экспериментальным данным Шошенко К. А. и соавт. (1982) по измерению скоростей
линейного кровотока в МС озерных лягушек.
При ![]() , можно рассчитать количество квантов крови
, можно рассчитать количество квантов крови ![]() в микрососуде между
двумя соседними МУ. Отношения
в микрососуде между
двумя соседними МУ. Отношения ![]() в реальных МС должны
приближаться к целым числам. Проведена проверка этой гипотезы, на рандомизированных
8-и микрососудах МС плавательной перепонки задней лапки озерных лягушек, из
которой следует, что
в реальных МС должны
приближаться к целым числам. Проведена проверка этой гипотезы, на рандомизированных
8-и микрососудах МС плавательной перепонки задней лапки озерных лягушек, из
которой следует, что ![]() приблизительно
равняется целому числу.
приблизительно
равняется целому числу.
Силы, вынуждающие квант
крови принимать сферическую форму есть силы поверхностного натяжения крови.
Таким образом, силы поверхностного натяжения также принимают участие в конфигурировании
МС.
Математическое выражение
«закона кубов» тождественно выражению, получившего в математике названия
«большой теоремы Ферма»: не существует
отличных от нуля целых чисел x, y, z, для которых имеет место равенство ![]() , где n>2. Теорема Ферма накладывает ограничения на
значение величин
, где n>2. Теорема Ферма накладывает ограничения на
значение величин ![]() ,
, ![]() ,
, ![]() в МУ: они не могут
одновременно быть целыми числами, т.е. относиться к множеству натуральных
чисел R.
в МУ: они не могут
одновременно быть целыми числами, т.е. относиться к множеству натуральных
чисел R.
Рассматривая реальные
соотношения между значениями ![]() ,
, ![]() ,
, ![]() в рандомизированных
23-х МУ плавательной перепонки задней лапки озерных лягушек с отклонением отношения
в рандомизированных
23-х МУ плавательной перепонки задней лапки озерных лягушек с отклонением отношения
![]() к
к ![]() порядка 10%, можно
сделать следующее предположение:
порядка 10%, можно
сделать следующее предположение:
При условии ![]() >
>![]() >
>![]() ,
,
![]() ,
,
где ![]() приближается к
среднему арифметическому
приближается к
среднему арифметическому ![]() и
и ![]() .
.
При условии ![]() >
>![]() >
>![]() ,
,
![]() ,
,
где ![]() приближается к
среднему арифметическому
приближается к
среднему арифметическому ![]() и
и ![]() .
.
Проведена проверка этой
гипотезы путем математического моделирования процесса распада кванта крови,
имеющего форму шара, при прохождении через МУ. Параллельно определялось
значение вурфа между величинами диаметров ![]() . Моделирование показало, что при условии
. Моделирование показало, что при условии ![]() >
>![]() >
>![]() существует только один вариант распада кванта крови
фиксированного объема на два других кванта, при котором выполняется «закон
кубов», справедлива высказанная выше гипотеза и при этом процентное отклонение
теоретического значения
существует только один вариант распада кванта крови
фиксированного объема на два других кванта, при котором выполняется «закон
кубов», справедлива высказанная выше гипотеза и при этом процентное отклонение
теоретического значения ![]() от фактического равно
0, что может являться проявлением оптимального распада кванта крови;
соответствующее значение вурфа для
от фактического равно
0, что может являться проявлением оптимального распада кванта крови;
соответствующее значение вурфа для ![]() ,
, ![]() ,
, ![]() не принадлежат к
вурфовой последовательности.
не принадлежат к
вурфовой последовательности.
6.
Синтетическая модель микрососудистых сетей
Реальные МС развиваются и
функционируют таким образом, что все структурно-динамические процессы в них
подчиняются принципу оптимальности. Они протекают таким образом, что при
множестве теоретических вариантов их осуществления, реализуются только те
варианты, при которых затрачивается минимальное количество материала и
энергии.
МС состоят из двух основных
структурно-функциональных элементов: микрососудов и МУ.
Микрососуд – первый основной
структурно-функциональный элемент МС, характеризуется следующими геометрическим
параметрами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , искривлением и пластичностью, отражающей динамику изменения
геометрических параметров. Общая длина микрососудов в МС человека составляет
величину порядка 105 км. Количество микрососудов
в МС большого круга кровообращения человека составляет величину порядка
2∙109.
, искривлением и пластичностью, отражающей динамику изменения
геометрических параметров. Общая длина микрососудов в МС человека составляет
величину порядка 105 км. Количество микрососудов
в МС большого круга кровообращения человека составляет величину порядка
2∙109.
Гемодинамический фактор
характеризуется следующими параметрами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , F, p, H,
, F, p, H, ![]() , E.
, E.
Поток крови представляет
собой непрерывный поток порций или квантов крови, следующих один за другим без
разрывов. Квант крови при прохождении через МУ стремится принять форму шара, с
диаметром ![]() под Действием сил
поверхностного натяжения крови, минимизирующих его поверхностную энергию и,
следовательно – поверхность. Число квантов крови, движущихся в микрососуде
определяется из соотношения:
под Действием сил
поверхностного натяжения крови, минимизирующих его поверхностную энергию и,
следовательно – поверхность. Число квантов крови, движущихся в микрососуде
определяется из соотношения:
|
|
МУ – второй основной
структурно-функциональный элемент МС. Общее количество МУ в МС большого круга
кровообращения человека составляет величину порядка 1,3∙109.
МУ характеризуется
фундаментальным параметром n – степенью ветвления, т.е. числом образующих его
микрососудов.
В реальных МУ n=3. Величина
3 является универсальной биологической константой ангиогененеза, обусловленной
принципом Рабля: «Эндотелий происходит только от эндотелия». Новый капилляр
образуется от уже существующего капилляра путем ответвления с последующей
канализацией. Образование МУ со степенью ветвления n>3 возможно только
теоретически. Поддержание и функционирование подобных структур сопряжено с
большими энергетическими затратами, в тоже время образование, поддержание и
функционирование МУ со степенью ветвления n=3 требует минимальных затрат.
Типы ветвления микрососудов,
описываемые в анатомической литературе, как «бифуркация», «ответвление»,
«дихотомическое деление», «микрососудистая бифуркация», «сосудистый тройник»,
являются синонимами МУ, со степенью ветвления n=3.
Типы ветвления микрососудов,
описываемые в анатомической литературе, как «трифуркация», «трихотомическое
деление», «мультифидное ветвление» являются частными случаями разветвления
микрососудов, при которых величина диаметра ветвящегося сосуда больше его
длины (![]() ).
).
Конфигурация МУ
характеризуется следующими геометрическим параметрами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , W.
, W.
Конфигурация МУ
характеризуется следующими гемодинамическими параметрами: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , F, p, H.
, F, p, H.
Геометрические и гемодинамические параметры, связаны между собой
универсальной моделью оптимальной конфигурации МУ.
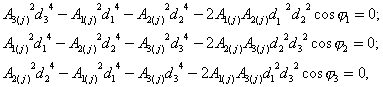
где j=1,2;
при j=1, Ai(1)=Hi; при j=2, Ai(2)=![]() ;
;
Hi и ![]() – соответственно полное
давление крови и коэффициент динамической вязкости крови в
– соответственно полное
давление крови и коэффициент динамической вязкости крови в ![]() -м микрососуде;
-м микрососуде;
![]() – диаметр
– диаметр ![]() -го микрососуда (
-го микрососуда (![]() <100 мкм);
<100 мкм);
![]() – угол между осями
симметрии просветов микрососудов, при этом
– угол между осями
симметрии просветов микрососудов, при этом
0< ![]() <180°,
<180°, ![]() ;
; ![]() = 1,2,3.
= 1,2,3.
Универсальная модель
оптимальной конфигурации МУ обусловлена биофизическими свойствами крови, модель
поведения которой в МС соответствует модели неньютоновской жидкости; а также
законом сохранения импульса (в общем случае – законом сохранения энергии) и
вещества.
Частным случаем
универсальной модели оптимальной конфигурации МУ при ![]() является модель C. D.
Murray:
является модель C. D.
Murray:
|
|
Эта
модель обусловлена биофизическими свойствами крови, модель поведения которой
соответствует модели ньютоновской жидкости, что имеет место в макрососудистых
сетях (![]() мкм). Из модели C. D. Murray следуют эмпирически
установленные для макрососудистого русла правила В. Ру (W. Roux).
мкм). Из модели C. D. Murray следуют эмпирически
установленные для макрососудистого русла правила В. Ру (W. Roux).
Из универсальной модели
оптимальной конфигурации МУ следуют количественные взаимосвязи между
структурными параметрами его конфигурации и параметрами гемодинамического
фактора, на основе которых работает механизм локального распределения и управления микропотоками крови:
|
|
где ![]() - некоторое значение.
- некоторое значение.
Конфигурация МУ обусловлена
физическим действием гемодинамического фактора в соответствии с универсальным
принципом симметрии П. Кюри.
Конфигурация МУ имеет
плоскость симметрии, в которой лежат и пересекаются в одно точке оси симметрии
трех микрососудов и которая делит ее на две зеркально равные половины.
Конфигурация МУ представляет
собой комбинированную фигуру, состоящую из фрагмента эллипсоида и трех
фрагментов круглых цилиндров, состыкованных таким образом, что их оси симметрии
лежат в одной из плоскостей симметрии эллипсоида и пересекаются в одной точке,
при этом каждый из трех углов, образующийся между этими осями, должен быть
меньше 180°, а в сумме они должны быть равны 360° (рис. 1).
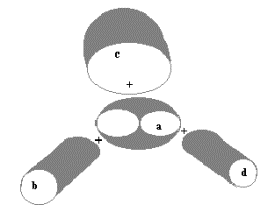
Рис.
1. Геометрическая модель формы просвета микрососудистого узла:
а
– фрагмент эллипсоида; b, c, d – фрагменты круглых цилиндров
Конфигурации МУ
подразделяются по виду количественных отношений между ![]() и
и ![]() на 52 класса, среди
которых существуют 26 зеркально-симметричных пар (табл. 1).
на 52 класса, среди
которых существуют 26 зеркально-симметричных пар (табл. 1).
Таблица 1.
65 теоретически возможных
классов конфигураций микрососудистых узлов по виду отношений
"больше–меньше–равно" между значениями ![]() и
и ![]() в конфигурации МУ
в конфигурации МУ
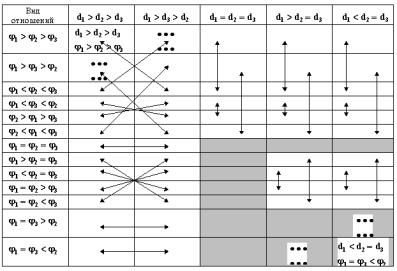
В результате наложения в
онтогенезе в одной и той же системе процессов построения тела человека в целом
и его внутренних систем по билатерально–симметричной схеме и синхронно
протекающих случайных процессов возникновения и конфигурирования МУ при
развитии МС, в конструкции последних появляются детерминированные свойствами
симметрии гемодинамического фактора и универсальным принципом симметрии П.
Кюри, ограничения на степень свободы ориентации МУ в тканевом пространстве,
которые в левой и правой половинах тела проявляются статистически как
зеркальные отражения друг-друга и имеют количественное выражение в виде разных
вероятностей принадлежности конфигураций случайно отобранных МУ из левой и
правой половины тела к классам зеркальных пар. Эти особенности конструкции МС
характеризуют их «правизну» и «левизну»
или хиральность, или энантиоморфизм и являются проявлением билатеральной
симметрии человеческого тела в макро-микроскопической области видения (табл.
2).
Таблица 2.
Теоретически возможные
комбинации отношений вида
"больше–меньше–равно"
между вероятностями P(Aj) и P(Aj')
того, что конфигурация
случайно выбранного МУ в МС из левой или из правой половины тела принадлежит
к j–ой зеркальной паре
|
Вид
отношений
|
P(Aj)r=P(Aj')r |
P(Aj)r>P(Aj')r<big><big> </big></big> |
P(Aj)r<P(Aj')r |
|
P(Aj)l=P(Aj')l </big></big> |
P(Aj)r= P(Aj')r P(Aj)l=P(Aj')l |
|
|
|
P(Aj)l>P(Aj')l |
|
|
|
|
P(Aj)l<P(Aj')l |
|
|
P(Aj)r<P(Aj')r P(Aj)l<P(Aj')l |
Aj и Aj' классы j–ой зеркальной
пары (j=1,2,3,...,26); P(Aj) и P(Aj') - соответствующие вероятности
того, что конфигурация случайно выбранного МУ в МС из левой или из правой
половины тела принадлежит к j–ой зеркальной паре. В табл. 2. приведено 9 теоретически возможных
комбинаций отношений вида "больше–меньше–равно" между вероятностями
P(Aj) и P(Aj') в одинаково ориентированных МС из левой (l) и
правой (r) половины тела. Исключены все комбинации отношений асимметричные по
отношению к плоскости ![]() и комбинация,
соответствующая симметрии шара. Клетки, в которых находятся оставшиеся
комбинации, не противоречащие универсальному принципу симметрии П. Кюри
заштрихованы.
и комбинация,
соответствующая симметрии шара. Клетки, в которых находятся оставшиеся
комбинации, не противоречащие универсальному принципу симметрии П. Кюри
заштрихованы.
Универсальный принцип
симметрии П. Кюри ограничивает многообразие конфигураций МУ (табл. 3).
Таблица 3.
Запрещенные (13 классов)
симметричные в плоскости ![]() конфигурации МУ, где
L3 – одна ось симметрии 3–го порядка, 3L2 – три оси симметрии 2–го порядка,4P –
четыре плоскости симметрии. L2 – одна ось симметрии 2–го порядка, 2P – две
плоскости симметрии
конфигурации МУ, где
L3 – одна ось симметрии 3–го порядка, 3L2 – три оси симметрии 2–го порядка,4P –
четыре плоскости симметрии. L2 – одна ось симметрии 2–го порядка, 2P – две
плоскости симметрии
|
Условия симметрии конфигурации МУ в плоскости |
Группа
симметрии конфигурации МУ в
плоскости |
|
|
|
|
|
|
|
|
|
|
|
«Закон кубов» ограничивает
многообразие конфигураций МУ. Параметры МУ ![]() ,
, ![]() ,
, ![]() связаны соотношением:
связаны соотношением:
![]() .
.
Теорема Ферма ограничивает
многообразие конфигураций МУ. Она накладывает ограничения на значения
величин ![]() ,
, ![]() ,
, ![]() : они не могут одновременно быть целыми числами, т.е.
относиться к множеству натуральных чисел R.
: они не могут одновременно быть целыми числами, т.е.
относиться к множеству натуральных чисел R.
При условии
![]() ,
,
когда ![]() >
>![]() >
>![]() , и
, и
![]() ,
,
когда ![]() >
>![]() >
>![]() , ограничивается многообразие конфигураций МУ.
, ограничивается многообразие конфигураций МУ.
Существует только одно
соотношение между диаметрами ![]() ,
, ![]() ,
, ![]() (
(![]() >
>![]() >
>![]() ) в МУ, при котором одновременно «работает» «закон кубов»,
справедливо соотношение
) в МУ, при котором одновременно «работает» «закон кубов»,
справедливо соотношение ![]() и процентное отклонение
и процентное отклонение
![]() от
от ![]() равно 0.
равно 0.
Реальные МУ в МС развиваются
в соответствии с общим принцип построения биологических тел из
конформно-симметричных блоков. Вурфы (W) образуют вурфовую последовательность,
имеющую отношение к числам Фибоначчи. Предел аффинной последовательности из
чисел Фибоначчи (1,618) называется золотым сечением, предельная величина
вурфовой последовательности (1,309) называется золотым вурфом. Вурф (W) отношения
диаметров ![]() ,
, ![]() ,
, ![]() в МУ определяется в
соответствии со следующими выражениями:
в МУ определяется в
соответствии со следующими выражениями:
При ![]() >
> ![]() >
> ![]()
![]() .
.
При ![]() >
>![]() >
>![]()
![]() .
.
Закон сохранения импульса (в
общем случае закон сохранения энергии) в парциальной или квантовой модели
движения крови через МУ, ограничивает многообразие соотношений между
параметрами ![]() ,
, ![]() ,
, ![]() в конфигурации МУ:
в конфигурации МУ:
0<![]() <180°,
<180°, ![]() ;
; ![]() =1,2,3.
=1,2,3.
Способность МС изменять
конфигурацию при изменении параметров гемодинамики и вновь принимать
оптимальную конфигурацию обусловлена пластичностью МС, которая определяется
структурно-динамическими свойствами микрососудистой (эндотелиальной) стенки,
связанной с ее чувствительностью к изменениям напряжения сдвига. Пластичность
МС имеет «норму реакции», которая может реализоваться в определенных пределах
в МС различных морфологических образований. Конфигурация МС всегда оптимальна
внутри «нормы реакции».
Динамика изменения
конфигурации МС имеет следующий примерный характер. При изменении диаметра
просвета одного из микрососудов микроциркуляторного модуля, происходит
изменение значения коэффициента динамической вязкости крови в этом
микрососуде, так как кровь по своим вязкостным свойствам соответствует модели
неньютоновской жидкости. Вследствие этого, конфигурации соседних МУ окажутся
неоптимальными для изменившихся условий гемодинамики и в силу своей
пластичности должны будут подстроиться, чтобы вновь принять оптимальные
конфигурации. Это приведет к изменениям параметров ![]() ,
, ![]() в конфигурациях этих
МУ. Подстройка и изменение конфигураций двух соседних МУ приведет к изменениям
в конфигурациях этих
МУ. Подстройка и изменение конфигураций двух соседних МУ приведет к изменениям ![]() ,
, ![]() в 4-х других соседних
микрососуда модуля, что в свою очередь приведет к нарушению оптимальности в
соседних 4-х МУ, которые в силу своей пластичности вынуждены будут
подстроиться, чтобы вновь принять оптимальные конфигурации. Далее процесс
распространится на 8 следующих соседних МУ модуля и т. д. В результате
разовьется цепная реакция подстроек, вследствие которой микроциркуляторный
модуль и МС в целом вновь примут оптимальную конфигурацию. Подобная реакция
разовьется при изменениях коэффициента динамической вязкости, давления,
конфигурации МУ или любой их комбинации. МС в результате цепных реакций
подстроек всегда будут принимать оптимальную конфигурацию при нормальных и
патологических состояниях организма. «Игра капилляров» или «игра микрососудов»
есть проявление этих цепных реакций подстроек.
в 4-х других соседних
микрососуда модуля, что в свою очередь приведет к нарушению оптимальности в
соседних 4-х МУ, которые в силу своей пластичности вынуждены будут
подстроиться, чтобы вновь принять оптимальные конфигурации. Далее процесс
распространится на 8 следующих соседних МУ модуля и т. д. В результате
разовьется цепная реакция подстроек, вследствие которой микроциркуляторный
модуль и МС в целом вновь примут оптимальную конфигурацию. Подобная реакция
разовьется при изменениях коэффициента динамической вязкости, давления,
конфигурации МУ или любой их комбинации. МС в результате цепных реакций
подстроек всегда будут принимать оптимальную конфигурацию при нормальных и
патологических состояниях организма. «Игра капилляров» или «игра микрососудов»
есть проявление этих цепных реакций подстроек.
В процессе функционирования
МС происходят сложные стохастические энергетические и динамические
морфологические процессы, связанные с превращением различных видов энергии (механической,
тепловой, электрической, осмотической, химической), сопровождающиеся
изменением конфигурации МС, подчиняющиеся общим законам термодинамики и теории
информации.
Сосудистые и микрососудистые
сети (МС) сердечно-сосудистой системы человека и животных представляют собой
единую фрактальную структуру, подчиняющуюся законам фрактальной геометрии.
Универсальной структурной единицей этой фрактальной структуры является МУ.
Сосудистые и микрососудистые
сети (МС) сердечно-сосудистой системы человека и животных представляют собой
граф - единую топологическую структуру, подчиняющуюся общим законам топологии
(теории графов).
7.
Ремоделирование МС в аутотрансплантате
селезенки крыс
В первую неделю после
аутотрансплантации фрагмента селезеночной ткани в большой сальник крысы,
начинается активизация процесса ангиогенеза. Происходит активное
новообразование сосудов со стороны большого сальника. При окраске азотнокислым
серебром по В. В. Куприянову в аутотрансплантате выявить сосуды не удается,
что свидетельствует о незрелости сосудов. Выявляются многочисленные
соединительнотканные волокна, внедряющиеся со стороны большого сальника в
ткань аутотрансплантата.
Формирование лимфоидных
фолликулов в периферической зоне аутотрансплантата говорит о возможной миграции
клеток лимфоидного ряда через новообразованные сосуды и о ведущей роли процессов
реваскуляризации в частичном восстановлении функции аутотрансплантата.
8. Биоимпедансометрические исследования МС селезенки крысы
В ходе исследования каждая
из 17-и селезенок делилась на 8 уровней для которых проводился замер
импеданса.
С помощью ранжирования
статистически с доверительным интервалом 0,95 удалось выявить, что минимальное
значение импеданса для одной селезенки достоверно отличается от следующего
минимального значения для этой же селезенки. Это говорит о том, что данные, получаемые
при БИМ одной селезенки достоверно отличаются друг от друга, что
свидетельствует о наличии, по крайней мере, восьми различных по своей
электропроводности зон в селезенке крысы.
БИМ позволяет
дифференцировать сосудистые сегменты в ткани селезенки, что может быть
использовано как при частичной резекции селезенки, так и для отбора хорошо
васкуляризированных фрагментов селезеночной ткани для аутотрансплантации.
9.
Исследование электрических явлений в низкоомных точках
на коже
человека
Анализ величины
электропроводности БАТ (точки: шао-шан, шао-чу и шао-фу) у живых (контрольная
группа) показал, что она в течение периода наблюдений (около 2,5 месяцев)
относительно постоянна с единичными спонтанными колебаниями.
Анализ величины
электропроводности НОТ (точки: шао-шан, шао-чу и шао-фу)
на трупах
(экспериментальная группа) показал, что она в течение периода наблюдений (около
суток) имеет тенденцию к снижению. В исследовании показателей
электропроводности НОТ у одного трупа до и после вскрытия обнаружилось, что
после проведения вскрытия они резко увеличились.
Прослежена
динамика изменения показателей электропроводности НОТ у 14 трупов с момента
наступления смерти. Оказалось, что прямой зависимости величины
электропроводности от времени, прошедшего с момента смерти до снятия этих
показаний, в выбранной нами группе не зарегистрировано. Это может быть
объяснено тем, что причины смерти у всех исследуемых были разными, и,
следовательно, были разными прижизненные показатели электропроводности,
поэтому посмертные показатели также различны. Такая вариабельность может
говорить о том, что каждая болезнь имеет свой спектр изменений электропроводности
БАТ (НОТ), который может быть использован для определения причин и времени
наступления смерти. Однозначно можно утверждать: у трупов обнаруживаются НОТ,
которые имеют ту же топографию на кожных покровах, что и БАТ у живых лиц;
наличие НОТ у трупов свидетельствует о том, что процессы связанные с
микроциркуляцией крови напрямую не связаны с электрическими явлениями в этих
точках.
ВЫВОДЫ
1.
Проверка модели C. D.
Murray на пленчатых препаратах МС париетальной плевры, твердой мозговой
оболочки, кожи, мышечных фасций, суставной капсулы, надкостницы длинных
трубчатых костей, надхрящницы, перикарда, брыжейки тонкой кишки человеческих
плодов и при биомикроскопии МС плавательной перепонки задней лапки озерных
лягушек показала, что эта модель не соответствует реальным конфигурациям МУ.
2.
Проверка «закона кубов»
для МУ МС плавательной перепонки задней лапки озерных лягушек, полученных при
анализе биомикроскопических данных, указывает, что этот закон выполняется в
исследованных МС. Модель C. D. Murray не
отражает конфигурацию реальных МУ, образованных микрососудами, имеющими диаметр
внутреннего просвета менее 100 мкм, и справедлива для конфигурации МУ,
образованных микрососудами и сосудами, имеющими диаметр внутреннего просвета
более 100 мкм. «Закон кубов» выполняется как в первом случае, так и во втором,
что указывает на то, что «закон кубов» обусловлен действием общих физических
законов: закона неразрывности струи или потока и закона сохранения вещества.
Теорема Ферма, впервые примененная для анализа конфигурации МУ, накладывает
ограничения на значение величин ![]() ,
, ![]() ,
, ![]() в МУ: они не могут
одновременно быть целыми числами, т.е. относиться к множеству натуральных чисел
R. Тем самым теорема Ферма накладывает ограничения на многообразие конфигурации
МУ.
в МУ: они не могут
одновременно быть целыми числами, т.е. относиться к множеству натуральных чисел
R. Тем самым теорема Ферма накладывает ограничения на многообразие конфигурации
МУ.
3.
Из универсальной модели
оптимальной конфигурации микрососудистого узла, созданной на основе
парциальной или квантовой модели движения крови через МУ, учитывая, что квант
крови под действием сил поверхностного натяжения крови стремится принять
форму шара, что обуславливает соотношение ![]() , можно получить систему из трех уравнений, описывающие
распределение скоростей потоков крови при прохождении через МУ:
, можно получить систему из трех уравнений, описывающие
распределение скоростей потоков крови при прохождении через МУ:
|
|
Полученная
система из трех уравнений имеет континуум решений относительно параметров ![]() ,
, ![]() ,
, ![]() :
:
|
|
Задав
значение скорости потока крови в одном микрососуде МУ, зная его параметры ![]() ,
, ![]() , однозначно получаем значения скоростей в двух других сосудах
МУ. Впервые удалось найти математические выражения, позволяющие вычислить
значения скоростей движения крови в микрососудах МУ, на основе их
конфигурационных параметров (
, однозначно получаем значения скоростей в двух других сосудах
МУ. Впервые удалось найти математические выражения, позволяющие вычислить
значения скоростей движения крови в микрососудах МУ, на основе их
конфигурационных параметров (![]() ,
, ![]() ). Расчетные отношения линейных скоростей
). Расчетные отношения линейных скоростей ![]() к
к ![]() в микрососудах МУ МС
плавательной перепонки задней лапки озерных лягушек хорошо согласуются с
литературными данными экспериментальных исследований измерению скоростей
линейного кровотока в МС озерных лягушек.
в микрососудах МУ МС
плавательной перепонки задней лапки озерных лягушек хорошо согласуются с
литературными данными экспериментальных исследований измерению скоростей
линейного кровотока в МС озерных лягушек.
4.
Экспериментальная
проверка отношения длины микрососуда к его диаметру показала, что это отношение
приближается к целому числу. В соответствии с парциальной или квантовой моделью
движения крови через МУ, это число равно числу квантов крови, движущихся в
микрососуде.
5.
Существует только один
вариант распада кванта крови фиксированного объема на два других кванта при
котором выполняется «закон кубов», справедливо соотношение ![]() и при этом процентное
отклонение
и при этом процентное
отклонение ![]() от
от ![]() равно 0, что может
являться проявлением оптимального распада кванта крови.
равно 0, что может
являться проявлением оптимального распада кванта крови.
6.
Синтетическая модель МС,
созданная на основе парциальной или квантовой модели движения крови через МУ,
позволяет объединить в единое целое комплекс описательных, экспериментальных и
теоретических данных, полученных с использованием принципа оптимальности,
универсальной модели оптимальной конфигурации МУ, универсального принципа
симметрии П. Кюри, теоремы Ферма, теории вурфов, термодинамики и теории информации,
теории фракталов, и теории графов.
7. После аутотрансплантации фрагмента селезеночной ткани в большой сальник крысы начинается активизация процесса ангиогенеза, происходит активное новообразование сосудов со стороны большого сальника, выявляются многочисленные соединительнотканные волокна, внедряющиеся со стороны большого сальника в ткань аутотрансплантанта. Формирование лимфоидных узелков в периферической зоне аутотрансплантата свидетельствует о возможной миграции клеток лимфоидного ряда через новообразованные сосуды и о ведущей роли процессов реваскуляризации в частичном восстановлении функции аутотрансплантанта.
8.
Данные БИМ селезенки
крысы достоверно свидетельствуют о наличии в ней, по крайней мере, восьми
различных по своей электропроводности зон.
9.
У трупа человека, по
крайней мере, в течение суток после смерти на коже обнаруживаются НОТ,
локализация которых совпадает с локализацией БАТ у живого человека. Наличие НОТ
на коже трупа человека свидетельствует о том, что процессы связанные с
микроциркуляцией крови, не связаны с электрическими явлениями в БАТ.
ПРАКТИЧЕСКИЕ РЕКОМЕНДАЦИИ
В процессе выполнения исследования были разработаны и
усовершенствованы следующие методики и устройства в области биомикроскопической,
анатомической (макро-микроскопической) и
гистологической техники, которые прошли апробацию и были внедрены на кафедре
анатомии человека, кафедре патологической анатомии и в ЦНИЛ Смоленской государственной
медицинской академии:
1.
Биомикроскопия
является наиболее предпочтительным методом регистрации МС для последующих
количественных исследований конфигураций МУ и МС в целом. Переходное кольцо
между бытовой цифровой видеокамерой Sony DCR-HC17E и микроскопом МББ–1,
позволяющее существенно упростить и удешевить видеорегистрацию МС при
биомикроскопии и способ определения параметров МУ при биомикроскопии,
позволяющий проводить измерение конфигурационных параметров МУ, формировать электронную
базу данных, проводить математическое моделирование МС, рекомендуется
использовать в морфологических и физиологических лабораториях, занимающихся
изучением микроциркуляции in vivo.
2.
Устройства для качественного пропитывания биологического материала
вакуумным методом и для засвечивания биологического материала, с последующей
дополнительной окраской, позволяющие выявлять коммуникационные пути в тканях
и органах, могут быть использованы в патогистологической технике для
исследования распространения патологических процессов в органах и тканях
3.
Способ
оценки соотношения красной и белой пульпы в гистологических препаратах
селезенки с помощью наливки МС черной тушью, с последующей компьютерной
обработкой цифровых фотографий гистологических срезов, позволяет существенно
упростить оценку соотношения красной и белой пульпы и может быть рекомендован в
экспериментальных исследованиях с использованием в качестве модели селезенки.
4.
Способ
определения полного электрического сопротивления (импеданса) биологических
тканей с применением оригинальных электродов можно использовать при проведении
точечной инвазивной биоимпедансометрии органов и тканей, позволяющей определять
показатели электропроводности отдельных участков. Для получения достоверных
результатов по БИМ селезеночной ткани достаточна выборка из 14 случаев, что
важно для дальнейшего планирования экспериментов по БИМ этого органа. БИМ может
быть использована для достоверной дифференцировки сосудистых сегментов в ткани
селезенки, что может быть применено при частичной резекции селезенки и для
отбора фрагментов селезеночной ткани для аутотрансплантации.
5.
Способ
диагностики травматического повреждения селезенки, основанный на точечной
инвазивной БИМ, позволяющий диагностировать неявные признаки повреждения
селезеночной ткани в условиях операционной и верифицировать ультразвуковые
данные при лапароскопическом исследовании, может быть рекомендован для
клинических испытаний.
6.
Оригинальная
экспериментальная установка для электрохимического лизиса и способ контроля
девитализации тканей при электрохимическом лизисе, основанный на БИМ, могут
быть использована в клинической практике для электрохимического лечения
новообразований и контроля процесса разрушения новообразований. Они существенно
упрощают лечебную процедуру и уменьшают стоимость лечения по сравнению с зарубежными
аналогами, могут быть рекомендованы к проведению клинических испытаний.
7.
Синтетическая
модель МС может быть включена в учебные курсы при изучении сердечно-сосудистой
системы в целом и системы микроциркуляции крови в частности.
СПИСОК РАБОТ, ОПУБЛИКОВАННЫХ ПО ТЕМЕ ДИССЕРТАЦИИ
1.
Смородинов
А. В. Опыт исследования электропроводности активных точек на кожных покровах
трупа человека. - Математическая морфология. Электронный математический и
медико–биологический журн. – Т. 3. – Вып. 1. – 1998. – URL:
http//www.smolensk.ru/user/sgma/MMORPH/N-4-html/12.htm .
2.
Смородинов
А. В. Исследование электропроводности низкоомных точек на кожных покровах трупа
человека / А. В. Смородинов // Тезисы докладов 1 Международной студенческая
конференции, посвященной 40-летию СНО Гродненского медицинского университета
(Гродно, 26-28 апреля 2000 г.). – Гродно, 2000. - С. 130-131.
3.
Смородинов
А. В. К вопросу о петлеобразующем росте кровеносных сосудов / А. В. Смородинов
// Проблемы возрастной и спортивной антропологии: материалы межрегионального
сборника научных трудов, посвященного 75-летию профессора Р. Н. Дорохова / под
ред. В. А. Быкова. – Смоленск, 2005. - С. 126 – 129.
4.
Смородинов
А. В. Моделирование микроциркуляторного русла, анализ существующих моделей
микрососудистых сетей / А. В. Смородинов // Материалы 33-й конференции молодых
ученых и 57-й научной студенческой конференции. – Смоленск: СГМА, 2005. - С.
63.
5.
Леонов
С. Д., Прудников И. М., Смородинов А. В. Импедансометрия селезенки. – Математическая
морфология. Электронный математический и медико–биологический журнал. – Т.
5. – Вып. 4. – 2006. - URL: http//www.smolensk.ru/user/sgma/MMORPH/N-12-html/smorodinov/smorodinov.htm http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-12-html/TITL-12.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-12-html/cont.htm .
6.
Смородинов
А. В. Использование метода импедансометрии при аутотрансплантации тканей
селезенки в эксперименте / А. В. Смородинов, С. Д. Леонов // Тезисы докладов
34-й конференции молодых ученых и 58-й научной студенческой конференции. –
Смоленск: СГМА, 2006. - С. 84.
7.
Бачерикова
А. Г., Прудников И. М., Смородинов А. В. Проверка закона Маррея для
микрососудистых сетей. - Математическая морфология. Электронный математический
и медико–биологический журнал. – Т. 5. – Вып. 4. – 2006. - URL: http//www.smolensk.ru/user/sgma/MMORPH/N-12-html/smorodinov-2/smorodinov-2.htm http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-12-html/TITL-12.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-12-html/cont.htm .
8.
Леонов
С. Д., Смородинов А. В. Перераспределение кровотока в бассейне чревного ствола
после спленэктомии / С. Д. Леонов, А. В. Смородинов // Вятский медицинский
вестник. – 2006. - №2. - С. 147.
Изобретения:
1.
Смородинов
А. В, Леонов С. Д. Электрод для проведения биоимпедансометрии (Приоритетная
справка 200613874604257 от 02.11.2006).
2.
Федоров
Г. Н., Леонов С. Д., Смородинов А. В. Способ диагностики травматического
повреждения селезенки (Приоритетная справка 2006138005041391 от 27.10.2006).
3.
Федоров
Г. Н., Леонов С. Д., Смородинов А. В.. Способ контроля девитализации тканей
при электрохимическом лизисе (Приоритетная справка 2006134770037835 от
02.10.2006).
Рационализаторские
предложения:
1.
Смородинов
А. В., Абросимов С. Ю. Устройство для качественного пропитывания
биологического материала вакуумным методом. Рациионализаторское предложение
№1429 от 12.11.2001. (Бриз СГМА).
2.
Смородинов
А. В., Абросимов С. Ю. Устройство для засвечивания биологического материала.
Рационализаторское предложение №1428 от 12.11.2001. (Бриз СГМА).
3.
Федоров
Г. Н., Гумиров Р. З., Смородинов А. В., Леонов С. Д. Способ определения
полного электрического сопротивления (импеданса) биологических тканей.
Рационализаторское предложение №1480 от 12.12.2005. (Бриз СГМА).
4.
Смородинов
А. В., Леонов С. Д. Электроды для измерения полного электрического
сопротивления (импеданса) биологических тканей. Рационализаторское предложение
№1482 от 02.02.2006. (Бриз СГМА).
5.
Смородинов
А. В. Переходное кольцо между бытовой цифровой видеокамерой Sony DCR-HC17E и
микроскопом МББ–1. Рационализаторское предложение №1483 от 01.03.2006. (Бриз
СГМА).
6.
Леонов
С. Д., Смородинов А. В. Способ оценки соотношения красной и белой пульпы в
гистологических препаратах селезенки. Рационализаторское предложение №1495 от
07.09.2006. (Бриз СГМА).
7.
Федоров
Г. Н., Леонов С. Д., Смородинов А.
В. Экспериментальная установка для
электрохимического лизиса. Рационализаторское предложение №1496 от 07.09.2006.
(Бриз СГМА).
8.
Смородинов
А. В. Способ определения параметров микрососудистых узлов при биомикроскопии.
Рационализаторское предложение №1501 от 22.01.2007. (Бриз СГМА).
СПИСОК ОСНОВНЫХ УСЛОВНЫХ СОКРАЩЕНИЙ
МЦР –
микроциркуляторное русло.
МС – микрососудистые сети.
МУ – микрососудистый узел.
МБ – микрососудистая бифуркация.
БИМ – биоимпедансометрия.
БАТ – биологически активная точка.
НОТ – низкоомная точка.
![]() ,
, ![]() ,
, ![]() - диаметры микрососудов в МУ (МБ).
- диаметры микрососудов в МУ (МБ).
![]() – радиус микрососуда.
– радиус микрососуда.
![]() ,
, ![]() ,
, ![]() - углы разветвления
между микрососудами в микрососудистой бифуркации
- углы разветвления
между микрососудами в микрососудистой бифуркации
![]() ,
, ![]() ,
, ![]() - скорости потока в
сосудах микрососудистой бифуркации.
- скорости потока в
сосудах микрососудистой бифуркации.
![]() - масса кванта крови.
- масса кванта крови.
![]() – плотность крови.
– плотность крови.
![]() – коэффициент
динамической вязкости крови.
– коэффициент
динамической вязкости крови.
![]() - длина сосуда.
- длина сосуда.
F – сила.
p – давление.
H – полное давление крови.
![]() - периферическое
сопротивление движению крови.
- периферическое
сопротивление движению крови.
![]() - число квантов
крови, движущихся в микрососуде.
- число квантов
крови, движущихся в микрососуде.
![]() – объем.
– объем.
![]() - группа симметрий.
- группа симметрий.
![]() – ось симметрии.
– ось симметрии.
![]() - плоскость
симметрии.
- плоскость
симметрии.
Кафедра анатомии человека
Смоленская государственная медицинская академия
Поступила
в редакцию 22. 02. 2007.
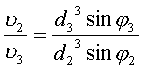 .
.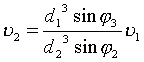
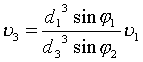
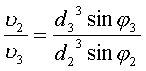 ;
;