УДК 681.322

 

О СХОДИМОСТИ РЕКУРСИВНОЙ КОМПОЗИЦИИ НЕЧЕТКИХ ОТНОШЕНИЙ

(fedulov.doc)

 

Ó 2007 г. Федулов А. С., Зуев М. Ф., Лаврухин В. С.

 

В работе задача исследования сходимости рекурсивной композиции нечетких отношений сведена к исследованию сходимости функциональной рекурсии и бинарных «четких» отношений. Для класса непрерывных монотонных функций получены теоретические результаты, позволяющие определять предел бесконечной функциональной рекурсии. Эти результаты использованы для определения предела рекурсивной композиции бинарных четких и нечетких отношений некоторых типов. Теоретические результаты подтверждены программным моделированием.

Ключевые слова: нечеткие отношения, непрерывные монотонные функции

 

ABOUT CONVERGENCE OF A RECURSIVE COMPOSITION OF FUZZY RELATIONS

Fedulov A. S., Zuev M. F., Lavrukhin V. S.

 

Theoretical results for limit of endless functional recursion in case of unceasing monotonous function are derived. These results are used to derive the limit of recursive composition of fuzzy relations (of some kinds). The theoretical results are confirmed by software simulations.

 

Введение

В настоящее время нечеткие системы находят широкое применение для решения сложных и слабо формализованных задач в различных областях деятельности [1]. В теории нечетких множеств важное значение имеет операция композиции нечетких отношений. Ее важность определяется, например, тем, что к этой операции можно свести продукционную нечеткую систему [2, 3].

Следует отметить, что в настоящее время недостаточно глубоко исследованы вопросы композиции нечетких систем, теории нечетких систем с обратными связями. Для создания нечетких систем с обратными связями требуется исследовать свойства рекурсивной композиции нечетких отношений. Таким образом, данная проблема является весьма актуальной.

Частично вопрос о свойствах рекурсивной композиции нечетких отношений для дискретного случая был рассмотрен в работах [4, 5].

 

1. Постановка задачи

Пусть задано бинарное нечеткое отношение  с функцией принадлежности , ; , - базовые множества действительных чисел. Будем полагать, что базовые множества ограничены некоторым интервалом действительной оси: . Под рекурсивной композицией будем понимать последовательное вычисление степеней отношения  следующим образом.

Определим нечеткое отношение  как нечеткую композицию нечетких отношений  и  (квадрат отношения ):

.                               (1)

Таким же образом определим и нечеткие отношения , …, :

,                               (2)

…,

.        (3)

…

Рекурсия, определяемая выражениями (1) – (3) может быть бесконечной.

Под сходимостью будем понимать существование предела:

.                                                            (4)

Как показал анализ, теоретическое определение предела (4) и условий его существования для нечетких отношений произвольного вида затруднено.

Целью данной работы является нахождение некоторых классов нечетких отношений, для которых возможно теоретическое исследование этого вопроса.

Для решения поставленной задачи в работе сначала рассмотрены вопросы сходимости функциональной рекурсии, а затем – бинарных «четких» отношений, к которым могут быть сведены a-уровни нечеткого отношения.

Теоретические результаты проиллюстрированы результатами моделирования.

           

2. Сходимость функциональной рекурсии

Пусть задано рекуррентное соотношение вида:

,                                                 (5)

где  – непрерывная функция, заданная на отрезке ,
 – начальная точка, =1, 2, 3, … .

Если итерационная последовательность (5) сходится, то ее предел  является неподвижной точкой отображения:

.                                                                     (6)

Действительно:

,                                    (7)

,                                           (8)

.                                                    (9)

Утверждение 1. Если на некотором интервале  выполняется

,                                                     (10)

то справедливо

.                                            (11)

Доказательство. Если начальная точка , то, очевидно, выражение (11) справедливо, так как  – неподвижная точка.

Пусть теперь начальная точка . Тогда из (10) следует, что

,                                    (12)

и

.                                                 (13)

Из (12) и (13) следует, что

.                                                       (14)

Таким образом, последовательность  является неубывающей. Кроме того, последовательность  ограничена сверху:

.                                                          (15)

Согласно признаку Вейерштрасса последовательность  сходится. Пусть

.                                                    (16)

Поскольку  – единственная неподвижная точка на интервале  и , то

,                                                                 (17)

что и требовалось доказать.

Утверждение 2. Если на некотором интервале  выполняется

,                                                          (18)

то справедливо

.                                             (19)

Доказательство утверждения 2 проводится аналогично доказательству
утверждения 1.

Пусть функция  на отрезке  имеет M неподвижных точек:

, , …, .                                (20)

Причем

.                  (21)

Тогда сходимость рекуррентного соотношения (5) будет описываться утверждениями 1 и 2.

В частности, если при переходе через точку  функция  меняет знак с «+» на «–», то  – точка притяжения:

.                                         (22)

Если при переходе через точку  функция  меняет знак с «–» на «+», то  – точка отталкивания:

,                                        (23)

.                                        (24)

Если при переходе через точку  функция  сохраняет знак «–», то  – точка левостороннего отталкивания и правостороннего притяжения:

,                                        (25)

.                                         (26)

Если при переходе через точку  функция  сохраняет знак «+», то  – точка левостороннего притяжения и правостороннего отталкивания:

,                                         (27)

.                                        (28)

Если в выражениях (22)–(28) точка  является крайней левой точкой притяжения, то есть, , то полагаем . Если же точка  является крайней правой точкой притяжения, то есть, , то полагаем .

На рисунке 1 представлен пример рекуррентного функционального соотношения (5) с пятью неподвижными точками.

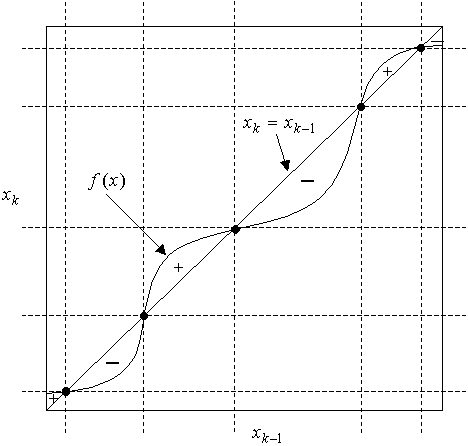
Рисунок 1. Пример неубывающей функции

 

2. Сходимость рекурсивной композиции бинарного отношения

Пусть задано бинарное «четкое» отношение  с функцией принадлежности вида:

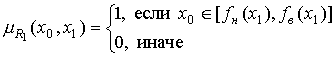,                                             (29)

где  – произвольные неубывающие функции, определенные на всей области определения переменной , причем .

Определим отношение  как композицию отношений  и :

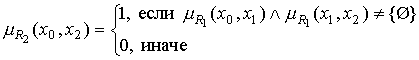.                        (30)

Таким же образом определим и отношения , …, :

 

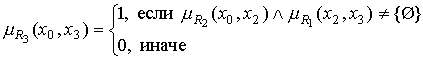,                       (31)

…,

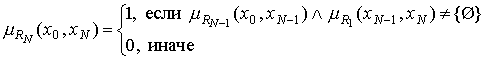.       (32)

Требуется условия существования следующего предела:

.                            (33)

Рассмотрим более подробно процесс получения отношения  , определяемого выражением (30).

Пусть переменная  – фиксированная. Тогда между произвольным значением  и данным значением  будет иметь место отношение , если

,                                             (34)

что показано на рисунке 2.

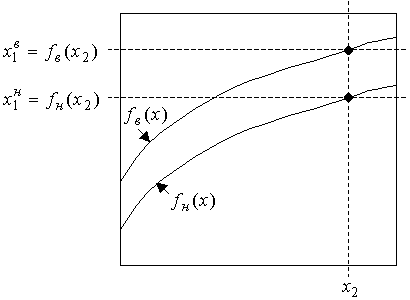
Рис. 2. Отношение

 

Теперь найдем значения переменной , при которых  и  находятся в отношении . Для этого необходимо определить минимальное  и максимальное  значения переменной , при которых имеет место отношение  между переменной  и переменной , удовлетворяющей ограничению (34).

В силу того, что  являются неубывающими функциями, значения  и  определяются следующим образом:

,                                            (35)

что показано на рисунке 3.

 

 

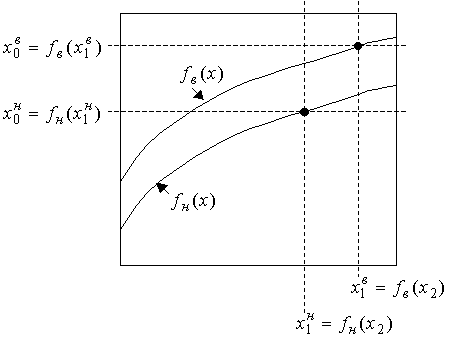
Рис. 3. Отношение

 

Перепишем (30) с учетом (34) и (35):

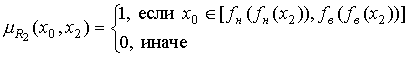.              (36)

Подстановка неубывающей функции в неубывающую функцию дает также неубывающую функцию.

Аналогичные рассуждения можно провести и для отношений , …, , в результате чего формулы (31), (32) можно представить в виде:

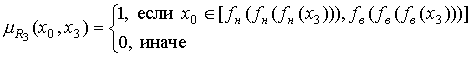,                       (37)

…,

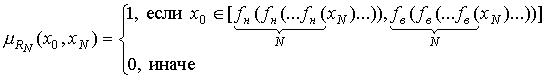.    (38)

Таким образом, вопрос о существовании предела (33) сводится к вопросу о сходимости рекуррентных соотношений вида:

,                                                (39)

.                                                (40)

Если соотношения (39) и (40) при  имеют пределы  и , соответственно, то искомый предел (33) будет определяться как:

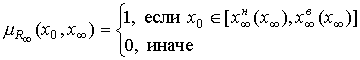.               (41)

Или с учетом ранее рассмотренного вопроса о сходимости рекуррентного функционального соотношения можно утверждать, что сходимость будет определяться неподвижными точками функций

 

3. Сходимость степени нечеткого отношения

Любое нечеткое множество, в том числе и нечеткое отношение, может быть представлено в виде объединения множеств -уровня [6]:

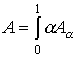.                                                              (42)

Таким образом, с учетом принципа обобщения Заде [6] cходимость степени нечеткого отношения определяется сходимостью степени множеств -уровня данного нечеткого отношения, то есть сходимостью четкого отношения, полученного из соответствующего множества -уровня.

 

4. Результаты моделирования

Рассмотрим класс линейчатых бинарных нечетких отношений, то есть нечетких отношений с функцией принадлежности, описываемой линейчатой поверхностью.

Ранее было показано, что для четких отношений, ограниченных неубывающими функциями сходимость степени отношения определяется сходимостью ограничивающих функций, то есть неподвижными точками данных функций.

То же утверждение можно расширить и для сходимости степени нечеткого отношения: сходимость степени нечеткого отношения определяется неподвижными точками функций, ограничивающих множества -уровня данного нечеткого отношения.

Для проверки данного утверждения был проведен ряд вычислительных экспериментов с различными дискретными линейчатыми нечеткими отношениями в среде MATLAB.

На рисунке 4 представлено исходное нечеткое отношение  и на рисунке 5 – нечеткое отношение, к которому сходится .

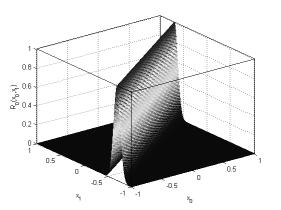
Рисунок 4. Нечеткое отношение

 

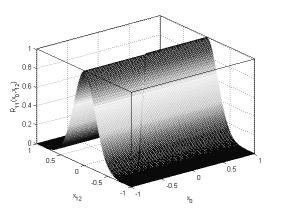
Рисунок 5. Нечеткое отношение, к которому сходится

 

На рисунке 6 изображено исходное нечеткое отношение  и на рисунке 7 – нечеткое отношение, к которому сходится .

На рисунке 8 представлено исходное нечеткое отношение  и на рисунке 9 – нечеткое отношение, к которому сходится .

Приведенные результаты подтверждают корректность представленных выше утверждений для отношений, ограниченных монотонными функциями.

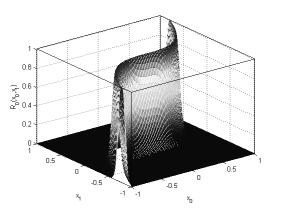
Рисунок 6. Нечеткое отношение

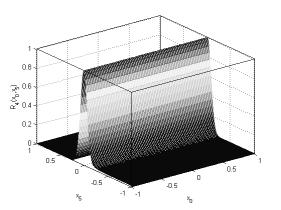
Рисунок 7. Нечеткое отношение, к которому сходится

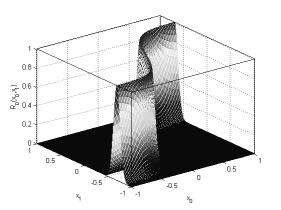
Рисунок 8. Нечеткое отношение

 

Для нечетких отношений, с функцией принадлежности линейчатого типа, у которых множества -уровня ограничены немонотонными функциями, в общем случае,  вопрос о сходимости остается открытым, поскольку данные функции могут иметь предельные циклы. Однако сходимость некоторых из таких отношений также подчиняется ранее сформулированным утверждениям.

 

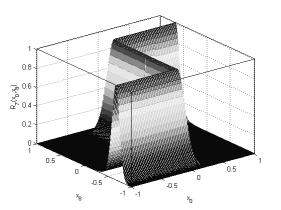
Рисунок 9. Нечеткое отношение, к которому сходится

 

Так, для нечеткого отношения  сходимость имеет место, как и в рассмотренных выше случаях (рисунок 10 и рисунок 11).

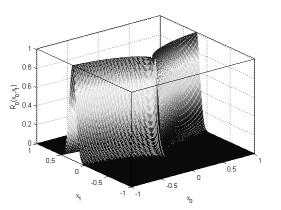
Рисунок 10. Нечеткое отношение

 

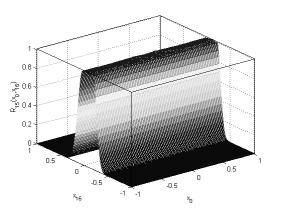
Рисунок 11. Нечеткое отношение, к которому сходится

 

То же самое касается и отношения (рисунок 12 и рисунок 13).

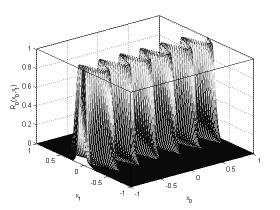
Рисунок 12. Нечеткое отношение

 

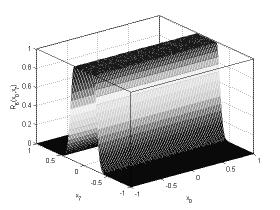
Рисунок 13. Нечеткое отношение, к которому сходится

 

Заключение

Проведен анализ сходимости функциональной рекурсии (для некоторых типов функций), получены условия ее сходимости. Проведен анализ сходимости рекурсивной композиции бинарных отношений (для некоторых типов отношений), получены условия ее сходимости.

Показана сводимость задачи о сходимости рекурсивной композиции нечеткого отношения к задаче в сходимости функциональной рекурсии.

Приведены результаты экспериментов в среде MATLAB, подтверждающие полученные результаты для нечетких отношений с множествами -уровня, ограниченными непрерывными монотонными функциями.

Показано, что подобные результаты имеют место и для ряда немонотонных функций.

 

Литература

  1. Борисов В. В., Круглов В. В., Федулов А. С. Нечеткие модели и сети. – М.: Горячая линия - Телеком, 2007.
  2. Кофман А. Введение в теорию нечетких множеств. – М.: Радио и связь, 1982.
  3. Федулов А.С. Нечеткие реляционные когнитивные карты // Известия РАН. Теория и системы управления, 2005, №1, с. 120–132.
  4. Zhou-Tian Fan, De-Fu Liu Convergence of the power sequence of a nearly monotone increasing fuzzy matrix. – Fuzzy Sets and Systems, 1997, vol. 88, pp. 363–372.
  5. Zhou-Tian Fan, De-Fu Liu On the power sequence of a fuzzy matrix (III). A detailed study on the power sequence of matrices of commonly used types. – Fuzzy Sets and Systems, 1998, vol. 99, pp. 197–203.
  6. Заде Л.А. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976.

 

Кафедра вычислительной техники

Филиал ГОУВПО «Московский энергетический институт (технический университет)» в г. Смоленске

Поступила в редакцию 12.04.2007.