УДК 681.322
оценка состояния объекта управления в случае
нечётко-множественной входной информации
Ó 2007 г. Зернов м. м.
В данной статье рассмотрены вопросы обработки нечёткими моделями
входной информации и получении на её основе некоторой оценки состояния
моделируемого объекта. Оценка по некоторому признаку выражается в виде степени
принадлежности входной информации классам состояний, описываемых
терм-множествами данного признака.
Особое внимание уделено случаю, когда входная информация
представляет собой непрерывную функцию принадлежности некоторого нечёткого
множества. Определены ограничения распространённых способов обработки подобной
информации, предложены способы их преодоления.
Ключевые слова: нечеткая логика, нечеткие ситуационные модели
object under control state evaluation in case of fuzzy-set incoming information
Zernov M. M.
The problems under
consideration in this article are: fuzzy models’ incoming information
processing and getting object under control state evaluations, based on this
information. Evaluation for some object property is figured out as incoming
information membership degree to states classes, described by the set of terms
of that property.
Special attention is put to the case, when incoming information represents an analog membership function of some fuzzy set. Limitations of spread ways of such information processing are defined, and the ways of such limitations overcoming are offered.
Практически во всех системах нечёткого логического вывода или нечётких ситуационных моделях первым этапом их функционирования является введение нечёткости (фаззификация) или иначе – оценка состояния некоторого моделируемого объекта или системы на основе совокупности лингвистических переменных, характеризующих его признаки.
Пусть 
- множество
признаков, описывающих состояние объекта управления, каждый элемент которого - 
- представляет собой
некоторую лингвистическую переменную 
, определённую на соответствующем базовом множестве 
и включающую терм-множество
, элементы которого определены как нечёткие переменные 
на указанном базовом
множестве, где 
- нечёткое
множество на 
.
Данные признаки, как правило, вводятся экспертным путём, а их терм-множества отражают некоторые классы возможных состояний объекта управления по каждому признаку.
В результате процесса оценки состояния, каждому терму из
терм-множеств всех лингвистических признаков ставится в соответствие некоторое
значение степени принадлежности входной информации (соответствующей указанному
признаку) классу состояний 
, описываемому данным термом.
В простейших FIS-структурах
данный этап тривиален – входные данные представляют собой чёткие числа 
- а значения 
определяются как
значения функций принадлежности соответствующих термов в точке [1]:
В общем же случае входная информация может носить разнородный характер, не ограничиваясь случаем чётких датчиков. Можно выделить три основных типа входной информации [2]:
- нечёткая (соответствующая словесному описанию от человека-оператор) – т.н. случай “нечётких датчиков”;
- чёткая (на вход системы поступают числовые данные от “чётких” датчиков);
- нечётко-множественная (представляемая в виде некоторой непрерывной
функцией принадлежности 
на базовом множестве
соответствующего признака) – т.н. случай “аналоговых датчиков”.
В случае нечётких датчиков человек-оператор сам указывает значения 
или непосредственно в
виде чисел из интервала [0; 1] или посредством слов, отражающих
соответствие состояние рассматриваемого объекта термам лингвистических значений
признаков (например “полностью соответствует”, “соответствует”, “совершенно не
соответствует”), которые в дальнейшем интерпретируются числами из интервала [0; 1].
В случае чётких датчиков, для сложных продукционных систем часто
используют универсальные шкалы значений признаков, что означает приведение
функций принадлежности терм-множеств всех признаков к отрезку [0; 1].
Для непосредственного использования данных шкал, они преобразуются посредством
функций отображения (например, линейных) в предметные (соответствующие
конкретным пределам базовых множеств). Значения 
определяются затем по
полученным предметным шкалам как обычно.
Случай “аналоговых” датчиков представляется наиболее сложным. Он
характерен для иерархических продукционных систем с отсутствующим этапом
дефаззификации между уровнями иерархии.[3] Входная информация относительно
некоторого признака 
при этом
представляется в виде некоторого нечёткого множества 
, характеризующегося функцией принадлежности 
на базовом множестве
признака.
При использовании универсальной шкалы для признака 
вначале производится
или отображение входного нечёткого множества на универсальную шкалу (см.
рисунок 1), или преобразование терм-множества признака в предметную шкалу,
соответствующую текущему базовому множеству признака. (см. рисунок 2).
Следующим этапом является последовательное сравнение членов терм-множества 
с входным множеством 
.
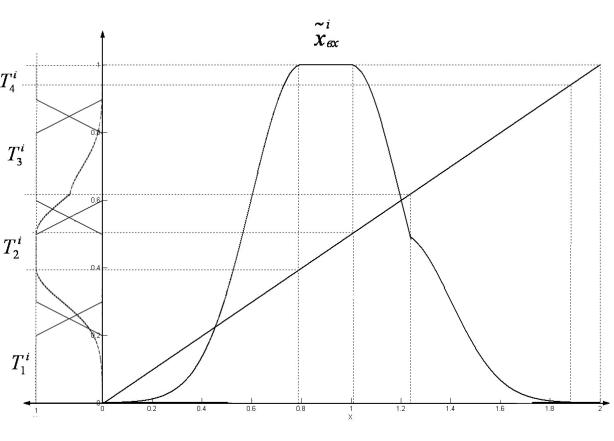
Рис.1. Пример отображения входного множества на универсальную шкалу
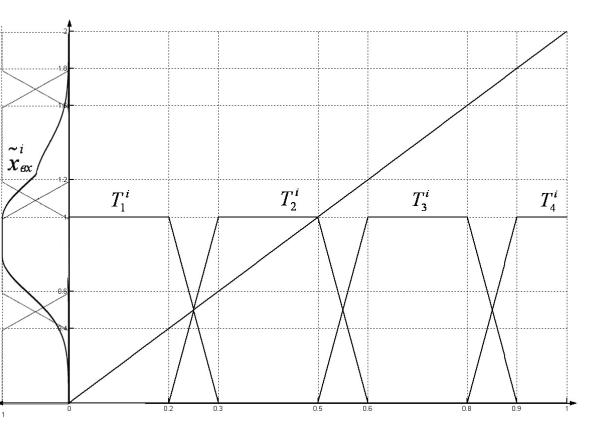
Рис.2. Пример преобразования универсальной шкалы в предметную
Наиболее распространён следующий способ данного сравнения. Вначале
вычисляется некоторая мера близости, представляющая собой нечёткое множество -
результат определённой операции F(
,
) над сравниваемыми
множествами, значение функции принадлежности которого в точке x определяется как операция f над
степенями истинности высказываний “x есть 
” и “x есть 
”, т.о. 
.[2]
Затем поточечные значения 
сворачиваются по некоторой T-норме 
, как правило, это 
.
В результате степень принадлежности 
входного множества 
рассматриваемому
терму 
определяется как 
.
В качестве F чаще всего используются следующие операции [2]:
- 
нечёткое включение входного множества 
в нечёткое множество
рассматриваемого терма 
, значение функции принадлежности результата которой
определяется как: 
(1), где 
- операция нечёткой
импликации.
- 
нечёткое равенство
(эквивалентность) входного множества и нечеткого множества рассматриваемого
терма, определяемое как: 
, где 
- операция
пересечения нечётких множеств, реализуемая некоторой T-нормой 
, связывающей значения функций принадлежности операндов в
каждой точке. В результате значение функции принадлежности образованного
множества определяется как: 
, выбрав для определённости в качестве связки & - min,
получим 
(2)
Выбор операции F зависит от требований, предъявляемых экспертом ко входному множеству, при выполнении которых оно может считаться соответствующим рассматриваемому терму. Нечёткого включение используется в случае, когда эксперту достаточно попадания входного множества в класс, описываемый термом. Нечёткое равенство характерно для случаев, когда эксперту требуется максимальное совпадение множеств.
Как следует из (1) и (2) конечный результат во многом зависит от выбора реализации операции импликации.
Наиболее распространены следующие математические представления импликации (указаны по фамилиям авторов их предложивших) [3]:
1)
Ларсен: 
;
2)
Лукасевич: 
;
3)
Мамдани: 
;
4)
Гёдель: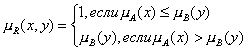 
;
5)
Клин-Дайнс: 
;
6)
Клин-Дайнс-Люк: 
.
Импликация по Ларсену и Мамдани не подходят для рассматриваемых целей, поскольку результат объединения поточечных мер близости отличен от нуля только в случае, если носители обоих множеств совпадают с базовым множеством.
Остальные варианты реализации импликации дают одинаково корректные
результаты для случая полного включения носителя входного множества во
множество модальных значений рассматриваемого терма (см. рисунок 3). Однако для
случая полного равенства рассматриваемых нечётких множеств импликации по Клину-Дайнсу и
Клину-Дайнсу_Люку дают заниженную оценку степени соответствия входного
множества терму 
(см. рисунки 4,5).
Всем рассмотренным реализациям способа нахождения 
для случая “аналоговых датчиков” характерно одно ограничение:
в ситуации, когда область модальных значений (или достаточно высокий
α-уровень) частично пересекается, а частично выходит за пределы носителей
двух смежных термов (см. рисунок 5), оценка степени соответствия входного
множества данным термам оказывается равной нулю, и нечёткая модель просто не
примет входные данные к рассмотрению.
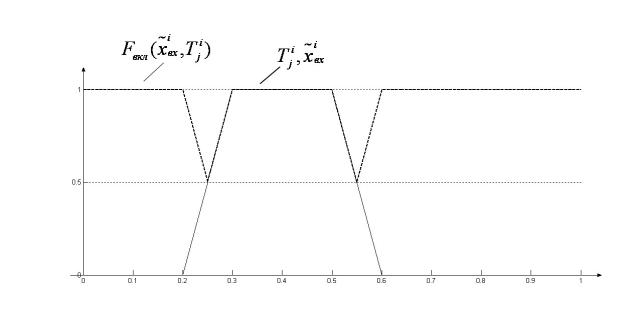
Рис. 3. Результат применения импликации по формуле Клина-Дайнса к двум одинаковым множествам
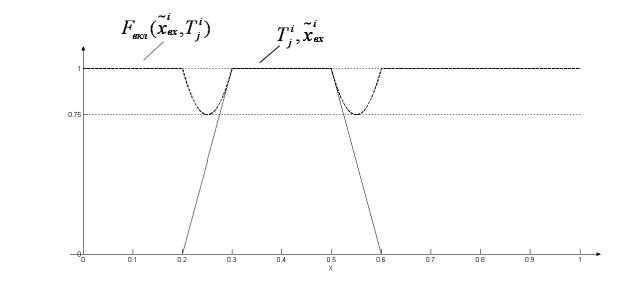
Рис. 4. Результат применения импликации по формуле Клина-Дайнса-Люка к двум одинаковым множествам
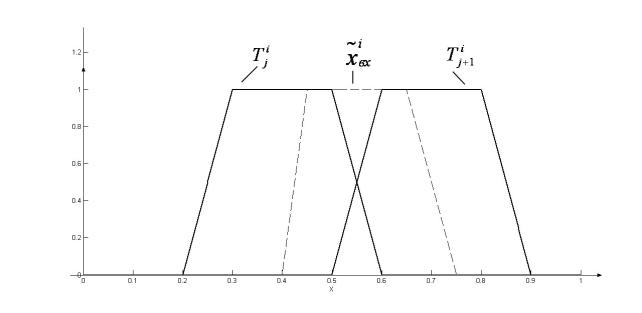
Рис. 5. Случай пропуска данных
Данное ограничение вызвано перечисленными выше требованиями, предъявляемыми
экспертом по отношению к входному множеству. На практике, довольно часто они
оказываются завышенными. Предлагается ь требования, предъявляемые ко входному
множеству в целом заменить на требования, предъявляемые к отдельным его
элементам. И вместо ответа на вопрос: “насколько относится 
к классу состояний признака 
, описываемому термом 
?” искать ответ на вопрос “есть ли среди элементов 
, относящиеся к классу состояний признака 
, описываемому термом 
?”.
Подобной постановке вопроса соответствует следующий вариант формулы
определения 
: 
, где 
- некоторая треугольная конорма. f, как и
ранее - операция над степенями истинности высказываний “x есть 
” и “x есть 
”, реализующая
некоторую операцию F, над указанными нечёткими
множествами, соответствующую некоторой мере одновременной принадлежности им
элемента x. В качестве конормы 
предлагается использовать: 
, поскольку данный вариант позволяет не завышать оценку 
. В качестве операции F, предлагается
использовать пересечение множеств 
, реализованное через операцию min, что в
свою очередь позволяет не занижать оценку
.
В результате построенная по вышеописанному способу значение степени
принадлежности входной информации классу состояний описываемому данным термом 
представляется в виде:
.
Заключение
В результате рассмотрения различных способов получения значения степени принадлежности нечётко-множественной входной информации некоторому классу состояний некоторого признака моделируемого объекта, определён ряд их недостатков.
Во-первых, выявлено несоответствие поставленной задаче распространённых способов реализации импликации по формулам Клина-Дайнса и Клина-Дайнса-Люка, при использовании их в таких мерах сравнения нечётких множеств, как нечёткое включение и нечёткое равенство.
Во-вторых, выявлено ограничение самого способа оценки степени принадлежности входного нечёткого множества некоторому терму нечёткого признака, при котором требование включения (или совпадения) накладывается на всё входное множество в целом. В результате нечёткая система “пропускает” входные нечёткие множества, множества модальных значений которых выходят за границы носителя рассматриваемого терма.
С целью устранения данного ограничения, предложены более мягкие требования к входному нечёткому множеству и способ нахождения степени принадлежности входной информации, им соответствующий.
Литература
1. Круглов В.В., Борисов В.В. Гибридные нейронные сети. Смоленск: Русич, 2001.- 224 с.
2. Мелихов А.Н., Берштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука, 1990.- 272 с.
3. Штовба С.Д. Введение в теорию нечетких множеств и нечеткую логику. Винница: Издательство винницкого государственного технического университета, 2001.- 198 с.
Кафедра вычислительной техники
Филиал ГОУВПО «Московский энергетический институт (технический университет)» в г. Смоленске
Поступила в редакцию 12.04.2007.