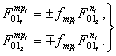- Математическая
морфология.
Электронный
математический и медико-биологический журнал. - Т. 6. -
Вып. 2. - 2007.
- URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-14-html/TITL-14.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-14-html/cont.htm
УДК 532.5+591.173+591.174
ББК 75.0
ОСОБЕННОСТИ
КОНТАКТА РУКИ ЧЕЛОВЕКА С ОПОРОЙ
Ó 2007
г. Покатилов А. Е., Загревский В. И., Попов В. Н.
При
выполнении упражнений на упругих спортивных снарядах, таких как перекладина или
женские брусья в гимнастике,
кинематические пары «рука – опора» идеальными не являются. В каждой паре
возникает трение, существенным образом влияющее на движение человека. Показано, что трение носит сложный характер
– оно является сухим трением, а ткани руки при этом проявляют упругие свойства,
существенным образом изменяя геометрию контакта.
Выявлены
основные теоретические зависимости в контактной зоне, характерные для случая перераспределения давления в контакте
руки человека с опорой за счет деформации биологических тканей. Показана связь
силы трения с направлением движения
спортсмена, выявлен механизм деформации спортивного снаряда за счет реакций в
кинематических парах «рука – опора», возникающих при выполнении спортивного упражнения.
Введение. На
первом этапе исследования движения человека все шарниры биомеханической
системы, включая и опорные, считаются идеальными, т.е. трением в них
пренебрегают [1, 2]. Это позволяет создавать достаточно работоспособные модели силового анализа, хотя и в неполной
мере отражающие действительную картину движения человека и его взаимодействия
со спортивным снарядом.
Многими
исследователями отмечалась сложность задачи учета трения в суставах человека
[2, 3]. Отметим его малую величину и относительно сложный характер. Определено
[3], что коэффициент трения в суставе здорового человека составляет 0,001–0,03.
Это очень малые значения. Природа создает устройства, более совершенные, чем
придумывает человек. Например, коэффициент трения в гидродинамических и прецизионных
подшипниках качения существенно выше. Установлено, что гидродинамический
эффект, позволяющий полностью разделить кости в суставе за счет слоя смазки, не
может объяснить столь малые величины, так как относительная скорость скольжения
между поверхностями костей никогда не превышает нескольких сантиметров в
секунду. А это слишком мало для создания разделяющего смазочного слоя.
Поэтому дополнительно были предложены
теории граничной смазки, просачивания и упругодинамической смазки. Эти механизмы являются основными в действии
смазки. Дополнительной формой смазки является сдавливание пленки между
сочленяющимися хрящами. Это сдавливание противодействует относительному сближению
костных поверхностей, особенно при малой толщине пленки (~0,25 мкм).
По
поводу трения в зоне контакта биомеханической системы и спортивного снаряда
отметим, что исследовать эту проблему хотя бы в первом приближении просто
необходимо. Причина в том, что управляемое движение в условиях опоры без трения
невозможно. Это показывают уравнения движения, записанные для случаев
целенаправленного движения биомеханической системы в условиях как жесткой [1],
так и упругой [4] опор.
Фрикционное взаимодействие руки с опорой. При описании процессов фрикционного взаимодействия
человека и спортивного снаряда применим ряд упрощенных моделей. В разделах
механики, занимающихся исследованием механизмов и машин, имеются устройства,
которые могут служить если и не в качестве аналогов, то, по крайней мере, в
качестве отправных точек для наших исследований трения. Это всевозможные
подшипники скольжения, изучаемые в деталях машин [5], теории механизмов и машин
[6] и в триботехнике [3]. Введем
ограничения. Считаем, что:
1.
объемные деформации
спортивного снаряда (опоры) пренебрежимо малы по сравнению с объемными деформациями
тела (руки);
2.
площадь контакта в паре
«рука – опора» в общем случае является величиной переменной;
3.
деформации контр-тела (руки) упругие;
4.
сила трения имеет
молекулярно-механическую природу;
5.
сила трения равномерно
распределена по ширине ладони;
6.
фрикционное
взаимодействие руки с опорой происходит в отсутствии смазки.
В работе
[5] рассмотрено трение во вращательной кинематической паре в условиях сухого
трения. Принятые допущения по трению в паре «рука – опора» несколько отличаются
от допущений, используемых при анализе трения в теории механизмов и машин, но
сам подход является весьма полезным и его можно взять на вооружение.
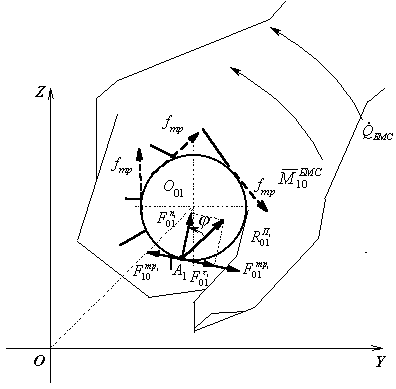
На опору в шарнире со стороны каждой руки
действует реакция 
(рис. 1). Так как
имеем два таких шарнира (по количеству рук), то возникающие реакции обозначим,
как 
и 
. Здесь 
и 
– это кинематические
пары, т.е. шарниры.
|
|
|||
|
Рис. 1 – Рука на
упругой опоре |
В общем случае, когда не надо
конкретизировать пару, реакцию будем
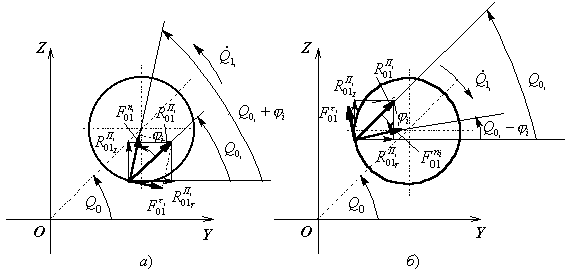
записывать с верхним индексом 
. Те же цифровые индексы относятся и к соответствующим
параметрам трения. Для анализа возьмем общий случай, считая реакции и трение в
шарнирах «рука – опора» различными. Также отметим, что опорные реакции
вращаются из-за вращения самой биомеханической системы, вызывая обращение
спортивного снаряда.
Реакции в каждом опорном шарнире
компенсированы 
. Здесь 
есть сила,
действующая со стороны опоры 0 на руку спортсмена 1 в шарнире 
, а реакция 
– результат действия руки 1 на опору 0 в том же шарнире.
Рассматривая направление сил, легко убедиться, что реакции связей 
действуют на балку со
стороны вогнутости упругой линии – ведь именно они и вызывают этот прогиб.
По поводу силы трения известно, что она всегда имеет направление,
противоположное относительной скорости движения [2-5]. Поэтому силы трения 
и 
равны между собой по
модулю и имеют противоположные направления, так как относительное движение рук
и упругой опоры противоположно.
Указано [3-6], что при изучении явления сухого трения
во вращательной кинематической паре пользуются различными гипотезами о законах
распределения нагрузки на поверхности элементов этой пары. Например, гипотезой
Вейсбаха о постоянных давлениях, гипотезой Рейе о постоянных износах и пр. Но у
них есть общий недостаток – отсутствует достаточное количество
экспериментального материала по вопросам распределения давления. Поэтому вывод
ограничивается простейшими формулами, сделанными на основе элементарнейших
предположений, схематизирующих явление.
Представим
расчетную схему на рисунке 2.
|
|
|||
|
Рис. 2 – Смещение опорной реакции |
Силовые возможности и конструктивные особенности руки таковы,
что боковой зазор между нею и опорой отсутствует, так как в отличие от
радиальных подшипников скольжения, кисть человека не является жесткой
конструкцией ни по материалу, ни по устройству. А, кроме того, за счет
управления мышцами имеется возможность прижимать руку к опоре, убирая зазор.
Тем не менее, его роль играет податливость тела. Поэтому предположим, что, как
и в случае с подшипниками скольжения, но только вследствие податливости тканей
руки, реакция 
смещается параллельно
самой себе (и реакции 
) и оказывается в
точке 
из-за «набегания»
руки на опору (рис. 2). Установленные при изучении механизмов и машин закономерности
трения таковы, что реакция 
должна быть отклонена
от нормали на угол трения 
, и величина силы трения 
получается равной
|
|
(1) |
|
|
где |
|
|
Здесь 
есть коэффициент
трения для плоских поверхностей из того же материала. Нормальная составляющая 
реакции 
по рисунку 2 равна
|
|
(2) |
Обозначение нормальной 
и касательной 
составляющих
специально изменено на букву 
вместо 
, так как в уравнение входит не общая реакция на опоре 
, а реакция 
в одном из двух
шарниров 
. Подобный шаг позволяет в дальнейшем избежать путаницы,
разграничивая общую опорную реакцию и реакции в отдельных шарнирах «рука –
опора» и их проекции.
При
использовании разрабатываемых моделей необходимо помнить, что силы трения и их
моменты, приложенные к руке и опоре, равны и противоположно направлены:
|
|
(3) |
.Движущий
момент, приложенный к руке 
, уравновешивается моментом трения 
. Найдем моменты, действующие на опору со стороны спортсмена:
|
|
(4) |
|
|
(5) |
Приравняв
моменты, получим
|
|
(6) |
|
|
где |
|
|
|
|
|
|
Указано [6], что если из центра 
описать радиусом r окружность (рис. 2), то реакция 
окажется направленной
по касательной к этой окружности. Получившийся круг радиуса r называется кругом
трения.
Считается,
что углы трения малы, поэтому можно принять
. На наш взгляд, данное положение применительно к
кинематической паре «рука – опора» нуждается в дополнительной проверке, тем более,
что для компенсации потоотделения и соответственно для увеличения трения
применяются присыпки, а также специальные накладки на руки. Но в качестве
первого приближения данное утверждение можно принять. Учитывая известное
соотношение 
для плоских
поверхностей [5, 6], запишем приближенное значение радиуса круга трения как 
.
При
силовом анализе биомеханической системы, определении деформации опоры и расчете
уравнения движения, записанного относительно спортивного снаряда, удобнее
считать опорную реакцию 
проходящей через
центр 
. Тогда надо дополнительно учесть момент сил трения 
во вращательной паре:
|
|
(7) |
|
|
где |
|
|
Сила трения 
необходима для более
точного расчета деформации спортивного снаряда при теоретическом нахождении его
прогибов, а момент 
вычисляется по уравнениям
целенаправленного движения и через него можно найти ряд параметров трения, если
перемещения опоры при изгибе
определялись экспериментально.
На
рисунке 2 показан случай вращения спортсмена по часовой стрелке и возникающие
при этом в опорной кинематической паре силы. Момент 
и сила 
действуют на разные тела.
Для
формулы (7) коэффициент трения 
находится
экспериментально для различных условий работы. Он носит еще одно название –
приведенный коэффициент трения [5]. Известно, что для случая внутреннего
касания цилиндрических поверхностей коэффициенты трения получаются больше, чем
для плоских поверхностей, приблизительно на 30%. К этому замечанию необходимо
отнестись достаточно критично, так как данные относятся, скорее всего, к
металлам. Ряд теорий для вращательных пар дают приведенный коэффициент трения в
пределах 
. Это тоже спорная для нас цифра, так как не учитывает специфику
контакта живого организма со снарядом. Тем не менее, тенденция хорошо видна.
Запишем
проекции силы трения через проекции опорной реакции в шарнире. При этом
необходимо рассмотреть два возможных случая движения биомеханической системы
относительно опоры.
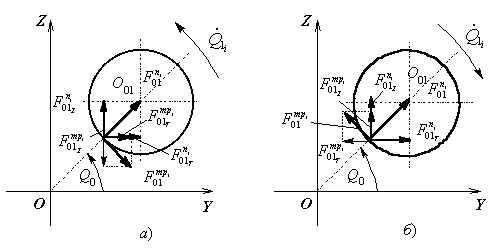
На
рисунке 3, а показан случай вращения
рук против часовой стрелки. Выполняется условие 
. На рисунке 3, б
выполняется условие 
, так как руки вращаются по часовой стрелке. Точка приложения
реакции 
смещается в зависимости
от направления вращения.
Проекции
нормальной силы 
по рисунку 3, а при 
определим как
|
|
(8) |
.Запишем угол, используемый для определения проекций на соответствующие
оси как 
.
При 
и угле 
по рисунку 3, б получим:
|
|
(9) |
.В уравнениях
использовано правило знаков, показанное на рисунках 3, а, б. Для подстановки в
эти выражения нормальной силы 
по формуле (2)
необходимо значение реакции 
в шарнире «рука – опора».
Удобнее ее выразить через проекции по рисунку 3, а для случая вращения рук по часовой стрелке и по рисунку 3, б для случая вращения против часовой стрелки как
|
|
(10) |
|||
|
|
||||
|
Рис. 3 – Опорная реакция и ее проекции |
||||
После
подстановки получим:
-
при 
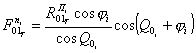или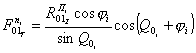 
,
|
|
(11) |
;-
при 
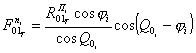или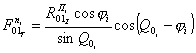 
,
|
|
(12) |
.Можно
уменьшить количество моделей за счет выбора направления отсчета угла 
. Согласно рисунку 3, а
при 
имеем 
, а по рисунку 3, б
при 
угол принимает
значение 
. Тогда в уравнения
подставляются углы 
со своим знаком.
Общие выражения имеют вид (11).
Правило
знаков для проекций силы трения. По поводу знаков проекций силы трения
необходимо отметить следующее: в работе [2] показано, что коэффициенты трения
для проекций силы трения в плоской декартовой прямоугольной системе координат
всегда имеют разные знаки. Это правило
можно записать как 
.
Приведем
для иллюстрации этой зависимости расчетные схемы на рисунках 4, а, б.
Их особенностью является тот факт, что реакция связи, действующая на опору,
показана без смещения относительно точки A, которую назовем точкой
несмещенного нагружения. Мы же
приняли гипотезу о параллельном смещении опорных реакций 
в каждой руке
относительно точки A.
Проекции
силы трения примут вид:
|
|
(13) |
Здесь возможно два варианта: 
и 
. Выбор конкретного
знака зависит от направления вращения рук спортсмена. При расчетах необходимо
помнить, что противоположность знаков относится к коэффициентам трения, а не к
проекциям 
и 
. Подставляя в уравнения (13) проекции 
и 
со своими знаками,
получим конкретные значения сил как совпадающие по знаку, так и
противоположные.
На
рисунках 4, а, б видно, что используемая для определения проекций силы трения нормальная составляющая опорной реакции 
всегда направлена по
радиусу исследуемого шарнира. Поэтому выводы о противоположности знаков
коэффициента трения при расчете проекций сил трения подтверждаются и для случая
параллельного переноса реакции.
|
|
|||
|
Рис. 4 – Проекции сил трения при вращении рук: а) против часовой стрелки; б) по
часовой стрелке |
Найдем соответствие
между направлением вращения рук относительно спортивного снаряда и применяемой
системой знаков для коэффициента трения (рис. 4, а, б). По рисунку 4, а при 
получим проекции силы
трения в виде
,
|
|
(14) |
Имеем вариант 
соответственно для
проекций на оси 
. В случае действия реакции на опору со стороны
биомеханической системы в любом другом квадранте полученное правило для знаков остается
таким же.
По
рисунку 4, б при 
имеем проекции силы
трения в виде
,
|
|
(15) |
Здесь реализуется вариант 
соответственно для
проекций на оси 
при осуществлении
контакта в любом квадранте. Занесем данные в таблицу 1.
Таблица 1
Правило
знаков проекций силы трения
|
Направление вращения рук |
Коэффициент трения скольжения
для осей OY/OZ |
Проекции силы трения |
|
|
|
|
|
|
|
|
Еще раз подчеркнем, что
знаки проекций силы трения, приложенной к спортивному
снаряду, определяются по направлению вращения рук спортсмена.
Подставим
в уравнения (13) выражения (11) с учетом правила знаков коэффициента трения.
Имеем:
или
,
или
|
|
(16) |
В
полученные выражения все параметры подставляются со своими
знаками.
Полную
величину силы трения в шарнире «рука – опора» найдем как
|
|
(17) |
На самом
деле фрикционное взаимодействие биомеханической системы и спортивного снаряда
носит более сложный характер. Так, следует отметить вероятное перераспределение
давления в контакте человека с опорой. Причем на данной стадии исследования
сложно судить о законе, которому подчиняется это давление. В качестве примера
приведем решение контактной задачи теории
упругости о сжатии цилиндрических поверхностей с близкими радиусами [5].
Закон распределения давления по контактной поверхности приближенно, но с
достаточной для практики точностью, аппроксимируют параболической зависимостью:
|
|
(18) |
|
|
где |
|
|
, отсчитываемым от линии действия усилия;
. В случае действия радиальной силы 
суммарная сила трения
и ее момент определяются как
|
|
(19) |
|
|
где |
m – коэффициент, зависящий от угла обхвата |
|
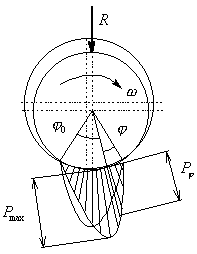
. Покажем
параболическую зависимость на рисунке 5. Конечно
же, использовать формулы (19) и методики определения коэффициента m для
случая, когда одно из контр-тел является эластичным, неправомочно. Мы лишь
показали непростой характер взаимодействия двух тел, в определенной степени
подобных нашей задаче по геометрическим признакам.
|
|
|
Рис.
5 – Распределение давления в контакте |
Отметим, что мягкие ткани руки являются
податливой средой, поэтому возможно образование валика перед контактной зоной.
Валик значительно влияет на трение. Такое поведение, например, демонстрируют полимерные подшипники качения.
Причем для образования валика совсем не обязательно движение в подшипнике –
достаточно просто радиальных усилий.
Несомненно, что при контакте руки со
спортивным снарядом тоже появляется валик во время движения, так как
поверхность руки в большей степени податлива и очень легко деформируется,
образуя складки, бугры и валики. В этом легко убедиться самостоятельно, просто
согнув ладошку. Использование специальных приспособлений, надеваемых на руки,
также может иметь свою специфику с точки зрения трения. Кроме того, в работе
условно принято, что ткани руки проявляют только упругие свойства. На самом деле деформационное поведение
человеческого тела более сложное, чем упругое.
Заключение. Таким образом, расчет сил трения, возникающих в зоне
контакта руки с опорой можно проводить методами, используемыми в теории
механизмов и машин при расчете подшипников скольжения при отсутствии смазки
(сухое трение)
Отметим следующие моменты: во-первых, при
расчете параметров трения нет необходимости уточнении модели опоры,
используемой для исследования целенаправленного движения человека (одна
вращающаяся или две поступательно перемещающихся пружин). Физическая природа
фрикционного контакта такова, что нам необходимо знание угла 
. Безразлично, с помощью каких моделей будет получен данный параметр,
но нужен именно он.
Во-вторых, контакт спортсмена со снарядом
может, как локализоваться на ограниченной площадке, так и быть максимально
большим, охватывая по периметру всю опору. В качестве примера приведем случай
хвата рукой за гриф перекладины. Соответственно на этой же площади
распределены и силы трения по какому-то
закону (конечно же, сложному).
В-третьих, в данной статье сделаны выводы
с определенными допущениями, т.е. они приблизительны, а также обозначены еще не
решенные проблемы фрикционного контакта человека со спортивным снарядом.
Thus,
calculation of forces of the friction arising in a zone of contact of a hand
with a support can be spent the methods used in the theory of mechanisms and
machines at calculation of bearings of sliding at absence of greasing (dry
friction)
Let's
note the following moments: first, at calculation of parameters of friction
there is no necessity specification of model of the support used for research
of purposeful movement of the person (one rotating or two it is forward moving
springs). The physical nature of frictional contact is those, that the
knowledge of a corner 
is necessary for us. It is indifferent, by means of what
models the given parameter will be received, but it is necessary.
Secondly,
contact of the sportsman to a shell can how to be localized on the limited
platform, is well maximal greater, covering on perimeter all support. As an
example we shall result a case хвата a hand for a
signature stamp of a crossbeam. Accordingly on the same area forces of friction
under any law (certainly, complex) are distributed also.
Thirdly,
in given clause are drawn conclusions with the certain assumptions, i.e. they
are approximate, and also not solved problems of frictional contact of the
person with a sports shell are designated yet.
ЛИТЕРАТУРА:
1.
Загревский, В. И. Расчетные модели кинематики и динамики биомеханических систем / В.И.
Загревский. - Томск-Могилев: Издательская лаборатория Томского педагогического
университета, 1999. - 156 с.
2.
Коренев, Г. В. Введение в механику человека / Г.В. Коренев. - М.:
Наука, 1977. - 264 с.
3.
Мур, Д. Основы и применения трибоники / Д. Мур. – М. : Мир,
1978. – 488 с.
4.
Покатилов, А. Е. Биомеханика взаимодействия спортсмена с упругой опорой / А.Е.
Покатилов ; под. ред. В.И. Загревского.
– Минск: Изд. центр БГУ, 2006. – 351 с.
5.
Дмитриев, В. А. Детали машин / В. А. Дмитриев. – Л. : Судостроение, 1970. – 792 с.
6.
Левитский, Н. И. Теория механизмов и машин / Н.И. Левитский. - М.: Высшая школа, 1990.
- 592 с.
Кафедра прикладной механики
Могилевский государственный технологический институт
Поступила в редакцию 21.06.2007.
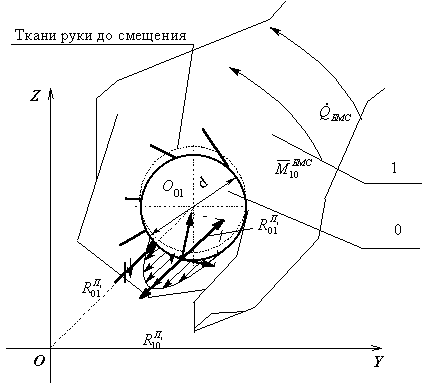
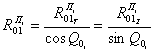
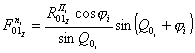
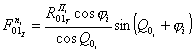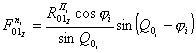
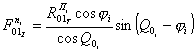