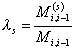Ó 2007 г. Попов В. Н., Покатилов А. Е., Загревский В. И., Лавшук Д. А.

(popov-3.doc)

В управляемом движении человека участвуют различные группы мышц: односуставные, двусуставные и многосуставные. При этом моменты управляющих сил, которые последние создают относительно каждого сустава биомеханической системы со стороны соседних звеньев равны только для односуставных мышц, для остальных равенства не наблюдается. Показано как при составлении уравнения целенаправленного движения методом кинетостатики приводятся управляющие силы двусуставных и многосуставных мышц к суставам, через которые они переброшены.

Проведена классификация возможных случаев возникновения сил в многосуставных мышцах, а также работа мышц антагонистов и их влияние на распределение моментов управляющих сил относительно суставов. Введены коэффициенты влияния мышц на движение звеньев, а также показана их динамическая природа. На примерах анализа техники спортивных упражнений в гимнастике сделан вывод о реализации мышечной и нервной системами каждого конкретного уравнения целенаправленного движения различными путями, зависящими от состояния спортсмена, его физической и технической подготовке и т.д.

Введение. С точки зрения управления различают естественное и целенаправленное движения. Естественное движение определяют как неуправляемое [1]. Оно не зависит от воли человека и решаемых им задач. Независимость означает подчинение только объективным законам механики. При естественном движении объект не вырабатывает управляющих воздействий.

На самом деле, движение человека отличается от естественного тем, что для управления внутри тела вырабатываются мышечные силы. Эти силы называются управляющими, а само движение – целенаправленным. Отметим, что если бы естественные движения достигали цели, то управление было бы не нужным [1, 2].

Таким образом, естественное и целенаправленное движения коренным образом различаются.

На сегодняшний день нет ответов на многие вопросы, относящиеся к возникновению управляющих воздействий в мышечном аппарате человека. В работах [1, 2] проведен анализ проблем целенаправленного движения. Отмечен недостаток, а порой и полное отсутствие в литературе по биомеханике, анатомии и антропологии данных по расшифровке действий мышечного аппарата во время совершения целенаправленных движений. Это касается и определения усилий, которые должны развивать мышцы для достижения определенных целей движения. По этой причине необходимо ввести определенные ограничения на модели движения, связанные с отсутствием надежных данных по прикреплению мышц к костям и по распределению усилий внутри области прикрепления, по распределению массы при деформации мышц во время движения, по подвижности суставов, по упаковке мышц и взаимном влиянии при прикосновении друг с другом.

Для вывода уравнений движения биомеханической системы используем принцип Даламбера. Модели принимают вид уравнений кинетостатического равновесия системы в виде суммы моментов силовых факторов, приложенных к звеньям и записанных относительно шарниров. Уравнения решаются относительно моментов управляющих сил мышечной системы.

Управляющие силы мышечного аппарата человека. Воспользуемся ограничениями, налагаемыми на модели мышечного аппарата и описанными в [1]. Считается, что они в основном правильно отражают суть проблемы, позволяя перевести исследование движения человека от общих рассуждений в практическую плоскость при нехватке точных знаний.

Принято:

- массой звена считать сумму масс костей скелета и мышц, примыкающих к кости;

- распределение масс внутри звена считать неизменным;

- тело мышц заменять линией действия мышечного усилия;

- считать, что движение обеспечивается минимальным количеством мышц, достаточным для обеспечения целенаправленного движения N-звенной системы;

- возможные взаимодействия между мышцами не учитывать.

Чаще всего управляющее воздействие обеспечивается не одной, а несколькими мышцами. Поэтому можно говорить о действии на звено целой группы управляющих сил – по числу мышц, участвующих в данном движении. Им противодействует такое же количество равных по величине сил, направленных противоположно и возникающих на звене, к которому мышцы прикреплены вторым концом. Управляющие силы попарно компенсируют друг друга. Действуя на каждое из звеньев, они дают два главных вектора управляющих сил, равных и противоположно направленных по одной общей линии.

Таким образом, вместо группы управляющих сил, приложенных к звену, будем иметь дело с одним главным вектором управляющих сил. Точка звена, через которую он проходит, не обязательно является местом прикрепления мышцы к кости, но такое представление удобно при исследовании целенаправленного движения.

Необходимо иметь в виду, что в общем случае управляющие воздействия, испытываемые каждым звеном, разбиваются на две группы, так как кроме первого и последнего звеньев все остальные имеют по два сустава, относительно которых и реализуется движение человека. Другими словами, для промежуточных звеньев движение относительно дистального сустава создают одни мышцы, и их действие описывается соответствующими силами, приложенными к данному звену. Движение относительно проксимального сустава происходит за счет других мышц и появляется вторая группа управляющих сил, также приложенная к рассматриваемому звену.

Целенаправленное движение биомеханической системы. Так как ни величина, ни направление, ни точка приложения к звену каждой управляющей силы неизвестны, то необходимо привести эти силы к соответствующему шарниру. Это позволит определить относительно его моменты управляющих сил.

В результате получим приложенные к шарниру силы реакции и управляющие силы, а также действующий на звено момент управляющих сил относительно шарнира (рис. 1). При этом на каждое звено также действует сила тяжести, и к нему присоединена инерционная нагрузка. Удобнее не приводить силу инерции i-го звена к точке качания, а показать ее приложенной в ЦМ звена. При этом возникает момент пары сил инерции.

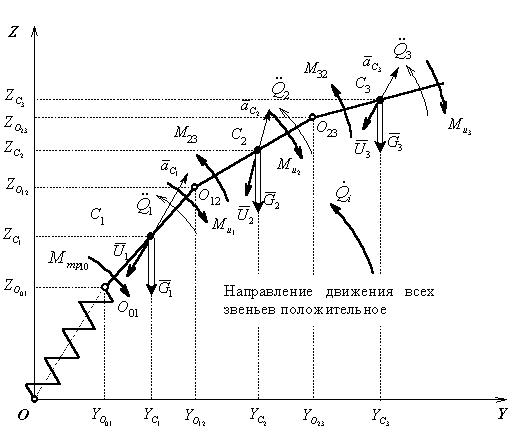
Покажем на рис. 1 все силовые факторы, используемые при выводе уравнений движения биомеханической системы [3]. Здесь моменты управляющих сил относительно суставов , , а также момент трения в опорном суставе показаны только со стороны анализируемой части биомеханической системы, и не показаны на соседних звеньях и на самой опоре.

Составим уравнения кинетостатического равновесия исследуемой части системы в виде суммы моментов относительно освобожденной кинематической пары. В этом случае для получения расчетной схемы необходимо последовательно отбрасывать звенья биомеханической системы со стороны опоры, как и при силовом анализе.

Для трехзвенной биомеханической системы относительно ее шарниров имеем:

(1)

Сразу выражая управляющие моменты мышечных сил и момент сил трения из уравнений кинетостатики, получим:

,		(2)
где	, , – моменты пар сил инерции звеньев 1, 2 и 3 соответственно относительно центра масс своего звена.

Для проекций сил инерции использованы выражения:

, .

Рис. 1 – Расчетная схема биомеханической системы (опора в виде

вращающейся пружины)

Знак минус относится к направлению рассматриваемых силовых факторов и уже реализован на рис. 1.

Опорный шарнир отличается от остальных, являющихся на самом деле суставами биомеханической системы. В отличие от них (в пределах принятых допущений), в кинематической паре возникают силы трения, и нет управляющих сил, приводимых к опоре, а значит, нет момента этих сил.

При этом необходимо учесть, что момент сил трения направлен против движения, что и показано на рис. 1.

Обозначим правую часть первого выражения системы (2) как . Это есть движущий момент всей биомеханической системы относительно спортивного снаряда. Его надо отличать от момента движущих сил, так как первый есть сумма моментов движущих сил и сил сопротивления, а последний является моментов только движущих сил.

Имеем . Знак минус означает, что моменты имеют противоположные направления при равенстве их значений.

Для сохранения однотипности формы уравнений движения относительно всех шарниров будем использовать для первого уравнения системы (2) запись момента через слева от знака равенства.

Запишем в общем виде уравнение для момента управляющих мышечных сил относительно шарнира :

,		(3)
где	i= 1, 2, …, N.

Отметим, что точкой приведения инерционных нагрузок является центр инерции , т.е. центр масс каждого звена. В этом случае дополнительно возникает момент пары сил инерции:

,		(4)
где	- центральный момент инерции j-го звена.

Знак минус означает, что направление дополнительного момента и углового ускорения звена противоположны. Выполнив преобразования, окончательно запишем для N-звенной системы момент управляющих сил относительно шарнира :

(5)

Здесь коэффициенты для трехзвенной системы приняты как:

(6)

Учтем, что при . Общее выражение для запишем как

(7)

1, если ,

0, если .

(8)

Здесь j, k – буквенные индексы. Они соответствуют цифровым индексам коэффициентов и равны:

j=1, 2, …, N; k=0, 1, …, N.

Коэффициенты для трехзвенной системы, взятой для анализа целенаправленного движения, определяются по уравнениям:

(9)

Здесь коэффициенты равны:

, если ,

, если i>j,

(10)

Анализ формул показывает, что коэффициенты при находятся в следующем отношении между собой: .

Влияние многосуставных мышц на целенаправленное движение. В предыдущем пункте исследовано целенаправленное движение без анализа функциональных возможностей мышечной системы. Отправной точкой полученных уравнений управляемого движения явилось приведение управляющих сил к шарнирам и написание уравнений кинетостатики с использованием моментов управляющих сил. Но при внимательном рассмотрении возникают вопросы о правомочности такого подхода. И вот почему. Некоторые мышцы перекидываются через один сустав, другие - через два, а третьи – через три. Различают односуставные, двусуставные и многосуставные мышцы [4, 5].

В качестве примера двусуставной мышцы можно привести двуглавую мышцу плеча, которая обеспечивает движение в локтевом (сгибает руку) и в плечевом суставах, а также супинирует (вращает наружу) предплечье.

Трехглавая мышца плеча, тоже являясь двусуставной, разгибает руку в локтевом суставе.

Задние мышцы бедра, перекидываясь через два сустава, сгибают ногу в коленном суставе и разгибают в тазобедренном. К многосуставным мышцам относятся полусухожильная, полуперепончатая и двуглавая мышцы.

Не вдаваясь в анатомические особенности прикрепления мышц, исследуем действие мышц антагонистов. Силу мышц антагонистов, вызывающих движение звена (звеньев), обозначим как управляющую силу с соответствующим индексом, например, . Силу, возникающую в мышцах антагонистах и компенсирующую полностью или частично действие соответствующих управляющих сил, обозначим, например, как . Здесь мышцы антагонисты, вызывающие целенаправленное движение, и мышцы антагонисты, препятствующие этому движению, есть разные мышцы. Например, двуглавая мышца плеча (бицепс) вызывает движение звеньев, а треглавая мышца (трицепс) этому движению препятствует.

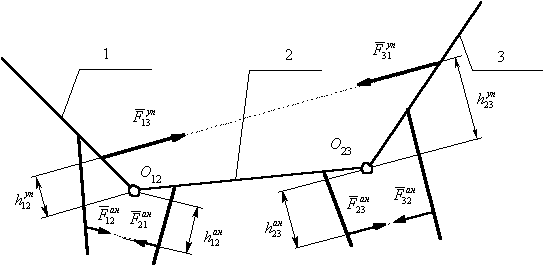
Рис. 2 – Управляющее действие двусуставных мышц

Рассмотрим трехзвенную систему и действие двусуставных мышц. Согласно схеме на рис. 2, движение звеньев 2 и 3 обеспечивается управляющими мышечными силами , . При этом силы равны по модулю и противоположны по направлению.

Предположим следующие варианты реализации движения за счет этих сил:

1. движение звеньев 2 и 3 происходит относительно сустава , при этом сустав зафиксирован;

2. движение звена 3 происходит относительно сустава , при этом сустав зафиксирован;

3. зафиксированных суставов нет, звенья 2 и 3 находятся в движении относительно звена 1.

На рис. 2 попарно обозначены силы , и , , возникающие в мышцах антагонистах, прикрепленных к соседним костям (звеньям). Здесь выбран вариант, когда управляющие мышцы антагонисты являются двусуставными, а мышцы антагонисты, препятствующие движению, – односуставные, так как это не принципиально. Получим следующую картину:

1. В случае равенства моментов относительно сустава , последний будет зафиксирован, и движение станет возможным лишь относительно сустава . Здесь:

, .

(11)

2. В случае равенства моментов относительно сустава , теперь уже он окажется зафиксирован, а движение можно реализовать лишь относительно сустава . Здесь:

, .

(12)

3. В случае, если ни один из суставов, через которые переброшены мышцы, вызывающие движение, не зафиксирован (, ), то получим движение относительно обоих суставов одновременно. Можно записать моменты, создаваемые силой , как:

, .

(13)

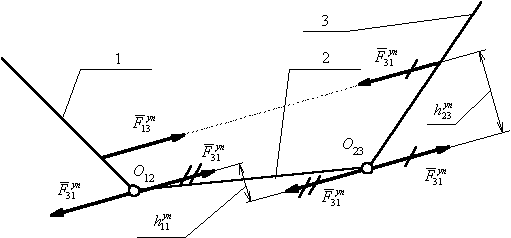
Для лучшего понимания п.3 воспользуемся правилом параллельного переноса силы. На рисунке 3 показан пример последовательного приведения управляющей силы многосуставной мышцы к суставам и , через которые переброшена данная мышца.

Рис. 3 – Приведение управляющей силы многосуставной мышцы к разным суставам

Сила вызывает вращение звена 3 относительно сустава с моментом . Приведение выполнено в пределах одного звена, т.е. жесткого тела, на которое эта управляющая сила действует [6, 7].

Так как по рисунку 3 сила , приложенная к суставу , действует как на звено 3, так и на звено 2, то выполним перенос силы в пределах уже этого звена в сустав . Получим дополнительный момент пары сил и управляющую силу мышечной системы , приложенную в суставе .

Таким образом, получен суммарный момент управляющих сил:

(14)

Тем самым показано, что одна и та же управляющая сила одновременно вызывает разные моменты относительно разных осей вращения, т.е. сила не распределяется между звеньями 2 и 3 – меняется лишь плечо соответствующего момента.

Во всех рассмотренных вариантах мы исходили из того, что моменты от сил в мышцах антагонистах, работающих на фиксацию сустава, меньше моментов управляющих сил или вообще отсутствуют. В противном случае картина не изменится, так как мышцы антагонисты, работающие на фиксацию сустава, начнут вырабатывать усилия, создающие целенаправленное движение. А управляющие мышцы антагонисты станут фиксировать движение в суставе или не будут оказывать никакого действия.

Здесь не исследовалась парадоксальная функция мышц, вследствие которой они косвенным путем производят движение в соседних суставах. Например, двуглавая мышца плеча, сокращаясь, сгибает руку в локтевом суставе, но при этом обычно натягивается трехглавая мышца, разгибающая руку в плечевом суставе.

Отметим, что при анализе работы мышечной системы мы не учитываем тоническое напряжение мышц, так как эти силы взаимно уравновешены.

Таким образом, многосуставные мышцы участвуют в движении звеньев относительно суставов, через которые они переброшены. Следующий вывод относится к работе мышц антагонистов: они могут перераспределять управляющее воздействие между звеньями за счет фиксации необходимых суставов, но не влияют на общую величину необходимых для движения моментов, вычисленных по выражениям (5).

На основании проведенного анализа работы мышечного аппарата сделаем следующий вывод: уравнения целенаправленного движения (5) отражают выполнение целей движения и не отражают напрямую работу мышц. Мозг человека сам решает, какими средствами и с помощью каких программ выполнить предложенные задачи целенаправленного движения.

По поводу программ, используемых мозгом для управления движением, в данной работе ничего говорить не будем. Относительно же действия мышечного аппарата человека заметим следующее: конкретная реализация необходимого движения зависит от многих факторов, например, от тренированности спортсмена, от спортивного упражнения и фазы, в которой находится спортсмен, его анатомических особенностей, его психологического состояния на данный момент времени и т.д. [2, 3, 8].

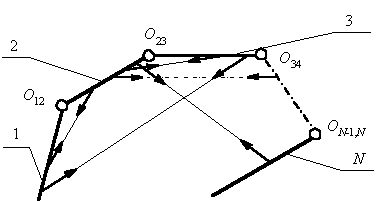
На рис. 4 представлен общий случай движения, когда используются как двухсуставные и многосуставные мышцы, прикрепленные к разным звеньям биомеханической системы, так и односуставные, прикрепленные к соседним костям человеческого тела.

Так как уравнения целенаправленного движения (5) позволяют найти моменты управляющих мышечных сил, которые являются суммой моментов одно-, двух- и многосуставных мышц, переброшенных через данный сустав и реализующих необходимое движение, то запишем выражение для момента как

,		(15)
где	, , – управляющие моменты мышечных сил, вырабатываемые относительно данного сустава соответственно одно-, двух- и многосуставными мышцами;
	u – максимальное количество суставов, через которые переброшена группа мышц, участвующая в создании момента относительно текущего сустава ;
	s – счетчик, s=1, 2, …, u. При этом ряд не является непрерывным, так как в каждом конкретном случае необязательно наличие многосуставных мышц с промежуточным числом суставов от 1 до u, через которые они переброшены.

Рис. 4 – Общий случай действия управляющих мышечных сил на биомеханическую систему

В наиболее общем случае каждый момент многосуставных мышц с конкретным числом s состоит из суммы моментов, количество которых равно числу мышечных групп, отличающихся звеньями (костями), к которым прикреплены начало и окончание мышцы. Замечание по поводу прикрепления мышц означает, что мышцы могут быть одинаковыми по количеству суставов, через которые они переброшены, но различаться звеньями, на которых крепятся (рис. 4). Запишем:

,		(16)
где	– управляющие моменты мышечных сил, вырабатываемые относительно данного сустава многосуставными мышцами с одинаковым количеством суставов s, через которые они переброшены, но с разным прикреплением;
	k=1, 2, …, p. Порядковый номер мышечной группы с одинаковым числом s;
	p – максимальное число мышечных групп с равным количеством суставов s, через которые они переброшены, но с разным прикреплением.

Тогда с учетом работы группы мышц относительно исследуемого сустава из уравнения (15) имеем:

,		(17)
где	– коэффициент влияния групп мышц синергистов, отличающихся количеством суставов, через которые они переброшены, на движение относительно текущего сустава. Определяется как
.		(18)

При этом понятно, что группа односуставных мышц полностью реализует момент управляющих сил , приходящийся на ее долю, так как у этих мышц нет возможности влиять на движение относительно других суставов. Остальные группы мышц синергистов являются многосуставными и создают момент управляющих сил в пределах величины согласно выражениям (15)-(17), но при этом имеют возможность участвовать в движении и относительно остальных суставов, через которые они переброшены.

Отметим также, что определение коэффициентов влияния групп мышц для управляющего момента мышечных сил, необходимого при реализации движения относительно конкретного сустава, и наличие фиксации сустава (перераспределение движения между суставами) выходит за рамки данной работы. Тем не менее, даже без подробного анализа проблемы видно, что сложность задачи определяется способностью человека управлять напряжением мышц во время движения. Другими словами, коэффициенты и фиксация суставов не являются постоянными параметрами движения, что переводит проблему в разряд трудно решаемых современными средствами исследования.

Такие же коэффициенты влияния можно ввести и для отдельных мышц, обеспечивающих движение биомеханической системы.

Заключение. Анализ полученных выражений, показывает следующие пути управления движением со стороны мышечной системы человека: изменение плеч моментов и величин управляющих сил, включение в работу новых мышц или выключение из нее задействованных. Осуществить это можно за счет избирательного напряжения и расслабления групп мышц, переброшенных через каждый сустав [2-5, 8].

При этом все мышцы, переброшенные через исследуемый сустав, решают задачу управляемого движения, записанную в виде уравнения движения. Типы мышц, классифицируемых по количеству суставов через которые они проходят, не учитываются в уравнении движения и поэтому у тела человека имеется возможность выбирать какими средствами решить задачу движения и достичь цели при управлении.

По поводу моментов отметим, что изменение расстояний от линий действия управляющих сил до суставов проявляется как результат управления напряжением мышечной системы, так и в качестве результата самого движения. Получается, что движение влияет на моменты управляющих сил, и наоборот. Другими словами, движение есть и следствие управляющего воздействия мышечной системы человека, и само влияет на это управление. Именно управляющие силы, вырабатываемые мышечной системой, и способы управления величиной и направлением их моментов относительно суставов являются причинами появления линейных и угловых скоростей и ускорений ЦМ звеньев биомеханических систем (т.е. движения), входящих в уравнения движения, а не наоборот. И во вторую очередь, кинематические параметры влияют на величину моментов управляющих сил.

The analysis of the received expressions, shows following ways of management of movement from muscular system of the person: change of shoulders of the moments and sizes of operating forces, inclusion in work of new muscles or deenergizing from it involved. To carry out it it is possible due to a selective pressure and a relaxation of groups of the muscles thrown through each joint [2-5, 8].

Thus all the muscles thrown through the investigated joint, solve the problem of the operated movement which have been written down in the form of the equation of movement. Types of the muscles classified by quantity of joints through which they pass, are not considered in the equation of movement and consequently the body of the person has an opportunity to choose what means to solve a problem of movement and to reach the purpose at management.

In occasion of the moments we shall note, that change of distances from lines of action of operating forces up to joints is shown as result of management by a pressure of muscular system, and as result of the movement. It turns out, that movement influences the moments of operating forces, and on the contrary. In other words, movement is also consequence of operating influence of muscular system of the person, and itself influences this management. The operating forces developed by muscular system, both ways of management in size and a direction of their moments concerning joints are the reasons of occurrence of linear and angular speeds and accelerations ЦМ of parts of biomechanical systems (i.e. movements), entering in the equations of movement, rather the reverse. And in the second turn, kinematic parameters influence size of the moments of operating forces.

ЛИТЕРАТУРА:

1. Коренев, Г. В. Введение в механику человека / Г. В. Коренев. - М.: Наука, 1977. - 264 с.

2. Загревский, В. И. Расчетные модели кинематики и динамики биомеханических систем / В.И. Загревский. - Томск-Могилев: Издательская лаборатория Томского педагогического университета, 1999. - 156 с.

3. Покатилов, А. Е. Биомеханика взаимодействия спортсмена с упругой опорой / А. Е. Покатилов ; под. ред. В. И. Загревского. – Минск : Изд. центр БГУ, 2006. – 351 с.

4. Боянович, Ю. В. Атлас анатомии человека / Ю. В. Боянович, Н. П. Балакирев. – Ростов на Дону.; Феникс, Харьков. : Торсинг, 2005. – 734, [1] с.

5. Фениш, Х. Карманный атлас анатомии человека на основе Международной номенклатуры / Х. Фениш (при участии В. Даубера). – Мн. : Вышэйшая школа, 2001. – 464 с.

6. Левитский, Н. И. Теория механизмов и машин / Н.И. Левитский. - М.: Высшая школа, 1990. - 592 с.

7. Никитин, Н. Н. Курс теоретической механики / Н. Н. Никитин. – М. : Высшая школа, 1990. – 608 с.

8. Бегун, П. И. Моделирование в биомеханике / П. И. Бегун, П. Н. Афонин. – М. : Высшая школа, 2004. – 390 с.

Кафедра прикладной механики

Могилевский государственный технологический институт

Поступила в редакцию 21.06.2007.