- Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 6. -
Вып. 2. - 2007. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-14-html/TITL-14.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-14-html/cont.htm
УДК 681.3
Реализация
матричной модели данных в иерархических структурах
Ó 2007 г. Сергеев В.
П.
В статье
рассматривается метод реализации матричной модели данных в иерархических
структурах. Рассматривается совокупность правил структурирования информации для
описания информации с помощью матричной модели данных. Функциональность матричной
модели данных описывается математическими методами манипулирования данными,
основанными на операциях алгебры многомерных матриц. Рассматриваемый, в статье, метод реализации матричной модели
данных в иерархических структурах, предоставляет аппарат для ее использования в современных СУБД.
Ключевые слова: матричные модели данных, многомерные
матрицы.
1. Введение
Основная идея статьи заключается в описании метода реализации в иерархических структурах инструмента представления и обработки информации, основанного на использовании математической структуры – алгебры многомерных матриц. С помощью этой алгебры, в 80-х годах, в работах [1, 2], были промоделированы операции обработки файлов, и приведено соответствие операций алгебры многомерных матриц, основным операциям обработки данных. Там же, был приведен теоретико-множественный подход к правилам структурирования информации для ее отображения в файлах и логических многомерных матрицах.
Рассмотрим описание матричной модели данных в следующем порядке:
1. описание правил
структурирования данных;
2. описание операций матричной модели данных.
Для реализации матричной модели в современных СУБД, автор предлагает способ представления многомерных матриц в иерархических структурах, т. к. последние позволяют избежать возникновения разреженности и являются более естественными для современных СУБД.
2. Построение правил структурирования данных
Предметная область состоит из некоторого множества
объектов X. Каждый объект 
, характеризуется некоторым набором k атрибутов, которые являются
значениями одноместных функций 
из множества
одноместных функций 
, заданных на множестве объектов X, 
.
Определим на
множестве X отношение эквивалентности R следующим образом: элементы 
и 
назовем
эквивалентными, если набор одноместных функций, определенных на 
и 
совпадает.
Отношение
эквивалентности R преобразует множество объектов X в фактор-множество X/R, состоящее из классов эквивалентности 
.
Каждый объект x из
класса эквивалентности 
, где i = 1, …, p должен содержать следующий набор атрибутов:
1. 
- значения
одноместных функций 
из множества
одноместных функций 
. Набор 
определяет класс
эквивалентности 
.
Добавим для
каждого объекта x три дополнительных атрибута.
2. 
- функция задает для
каждого объекта дополнительный атрибут – его индивидуальный идентификатор.
3. 
- функция задает для
каждого объекта дополнительный атрибут – его порядковый номер в классе
эквивалентности 
, где i = 1, …, p. Областью значения функции 
является множество
натуральных чисел.
4. 
- функция задает для
каждого объекта дополнительный атрибут – его представление. Областью значений
для этой функции является некоторый кортеж из атрибутов объекта, т. е. значений
функций 
.
Рассмотрим декартовое произведение некоторого набора
классов эквивалентности 
из классов эквивалентности
фактор-множества X/R. В декартовом произведении классы
эквивалентности могут повторяться. Функция 
, областью
определения которой является набор кортежей 
рассматриваемого
декартового произведения, сопоставляет каждому кортежу некоторое значение a. Каждому объекту x (по построению) присущ атрибут 
, следовательно, каждое значение функции 
можно представить
следующим образом 
. Значения, представленные таким образом, можно интерпретировать
как элементы n – мерной матрицы 
, где значением элемента 
матрицы, будет являться значение функции 
, а значениями каждого из индексов 
элемента 
матрицы будут атрибуты объектов 
соответственно.
Каждый индекс 
матрицы
принимает значения от 1 до количества объектов соответствующего класса эквивалентности
.
Определим правила структурирования данных произвольной предметной области:
1. Факторизация множества объектов предметной области по отношению эквивалентности R;
2.
Конструирование дополнительных функций 
, 
, 
;
3. Построение многомерных матриц.
3. Описание
методов обработки информации
К многомерным
матрицам и множествам (классам эквивалентности) объектов, построенным с помощью
описанных трех правил структурирования данных, применимы математические
операции алгебры многомерных матриц и теории множеств. В таблице 1 показана
взаимосвязь операций алгебры многомерных матриц с основными операциями обработки
данных для файлов [1, 2] и операций реляционной модели.
Табл.1. Взаимосвязь операций
|
Операции над файлами |
Операции алгебры матриц |
Реляционные операции |
|
Сортировка |
Транспонирование |
нет |
|
Выборка |
Сечение |
select |
|
Сжатие |
Свертка |
project |
|
Слияние
строгоупорядоченных файлов |
Сложение |
Теоретико-множественные
(объединение, пересечение, разность) |
|
Слияние нестрого
упорядоченных файлов |
Умножение |
join |
Так как многомерные матрицы представляют собой многомерный структурированный массив информации, то можно говорить о том, что матричная модель данных является многомерной. Это следствие указывает на то, модель предметной области, построенная с помощью матричной модели, без каких-либо дополнительных надстроек, предоставляет математический аппарат многомерного анализа информации. Бинарные операции предоставляют возможность анализировать не только информацию, хранящуюся в каждой отдельной многомерной матрице, но и информацию, хранящуюся во всех матрицах в целом. При этом возможно использовать математический аппарат алгебраических выражений, позволяющий оптимизировать порядок следования операций для уменьшения количества процессов обработки информации.
Методы матричной обработки информации, в силу присутствия в них большого числа циклических процессов, обладают высокой степенью распараллеливания, следовательно, к ним можно применить технологии распараллеливания, что позволит еще больше повысить их производительность.
4. Реализация матричной модели данных в современных СУБД
Реализация
матричной модели данных в современных СУБД подразумевает ряд сложностей. Сложности
связаны в первую очередь с тем, что многомерные матрицы представляют собой, в
большинстве случаев, огромный многомерный разреженный массив структурированной
информации. Работать с такими многомерными массивами не совсем оправданно и,
следовательно, необходимо нахождение других структур, хорошо реализованных в
современных СУБД и позволяющих моделировать как сами многомерные матрицы, так и
их операции. Такими структурами являются иерархические структуры. В работах
автора [3, 4, 5] рассмотрен метод иерархического представления алгебры многомерных
матриц.
Любую многомерную
матрицу можно представить в виде связной иерархической структуры ее сечений. Рассмотрим
матрицу 
, где 
(
соответственно). Сечением 
матрицы будет
множество элементов с координатами 
, где 
, при этом, один или несколько индексов будут фиксированными.
Назовем сечениями l уровня -
сечения, полученные из матрицы A, фиксацией значений индексов 
.
Для произвольной
многомерной матрицы, количество уровней разбиения на сечения, а также количество
самих сечений будут определяться из размерности матрицы. Уровней разбиения
будет столько же, сколько индексов в многомерной матрице - p. Общее количество сечений всех уровней будет равно 
. Количество сечений l уровня будет равно 
.
Рассмотрим
произвольную трехмерную матрицу 
, где 
(рис. 1).
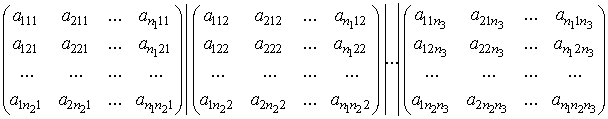
Рис. 1. Матрица 
Для данной матрицы
уровней разбиения будет три.
Сечений первого
уровня будет 
: 
, 
, …, 
.
Сечений второго
уровня будет 
: 
, 
, …, 
.
Сечений третьего
уровня будет 
: 
, 
, …, 
.
Рассмотрим матрицу 
, где 
. Разобьем эту матрицу на сечения поэтапно по количеству
элементов в каждом ее индексе. Покажем, как будет выглядеть разбиение
пространственной модели этой матрицы (рис. 2).
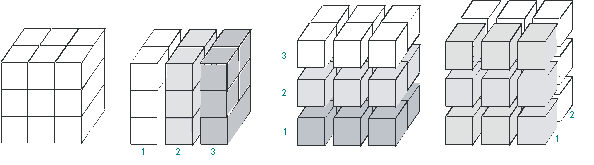Рис. 2. Разбиение пространственной модели
Для матрицы, уровней
разбиения всего три.
Сечений первого
уровня будет 3: 
, 
, 
.
Сечений второго
уровня будет 3*3=9: 
, 
, 
,
, 
, 
, 
, 
, 
.
Сечений третьего
уровня будет 3*3*2=18: 
, 
, 
,
, 
, 
, 
, 
, 
, 
, 
, 
,
, 
, 
, 
, 
, 
.
По разбиению, видно,
что сечениями последнего уровня будут являться сечения, содержащие индексы
всего лишь одного элемента. Сопоставим каждому такому сечению – значение этого
элемента многомерной матрицы. Иерархическая структура будет выглядеть следующим
образом (рис. 3).
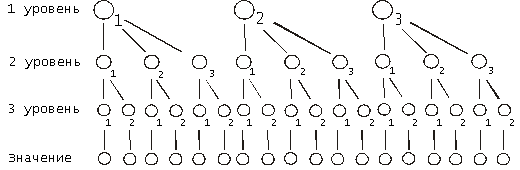
Рис. 3.
Иерархическая структура рассматриваемой матрицы (вместо сечений записаны их
фиксированные индексы соответствующих уровней)
Введем некоторое
ограничение на алгебру, множеству которой принадлежат значения элементов многомерной
матрицы.
Далее будем
рассматривать только многомерные матрицы, значения элементов которых являются
элементами алгебры, для которой выполняются следующие условия:
1.
Алгебра 
- множество M с заданными на нем двумя бинарными операциями 
и 
.
2.
Закон симметричности и наличие нейтрального элемента
выполняются для операций 
и 
.
3.
Нейтральный элемент по операции 
является обнуляющим элементом
по операции 
, т. е. существует такой элемент 
, при котором 
и 
.
Элемент e играет важную роль в последующем изложении.
Назовем этот элемент нулем. К примеру, для поля
действительных чисел, таким элементом будет являться 0. Для поля логических
элементов – элемент «ложь».
Сечение многомерной
матрицы назовем актуальным, если оно содержит хотя бы один набор индексов
элемента многомерной матрицы, не равного нулю. Иерархические структуры
многомерной матрицы будем строить только из актуальных сечений.
Предположим, что
рассматриваемая матрица имеет всего три элемента, не равных нулю, индексы которых
(1, 1, 1), (1, 1, 3) и (2, 2, 3).
На рис. 4 показана
иерархическая структура актуальных сечений рассматриваемой матрицы.
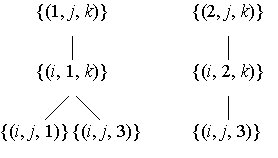
Рис. 4. Иерархическая структура актуальных сечений
матрицы
Иерархическая структура представляет собой
граф. При данном представлении, иерархическая структура такого рода,
определяется совокупностью полных путей графа, так как любых два полных пути
иерархической структуры не совпадают, каждый в отдельности характеризует единственный
элемент многомерной матрицы, а в совокупности образуют совокупность элементов, не равных нулю, с соответствующими
индексами представленной иерархической структурой.
Определение
1: Элементом иерархического представления
многомерной матрицы 
назовем полный путь иерархической структуры (графа), и обозначим его 
.
Определение
2: Иерархическим представлением многомерной
матрицы 
, индексы элементов которой 
принимают
значения от 1 до 
соответственно, назовем иерархическую
структуру, построенную указанным способом, и обозначим ее 
, которая задается совокупностью элементов 
.
Иерархические структуры, рассмотренные в
данной статье, могут применяться для хранения разреженных матриц. При таком
способе представления многомерных матриц, осуществляется не только хранение
элементов не равных нулю, но и хранение структуры многомерной матрицы, что
позволяет осуществить операции алгебры многомерных матриц над иерархическими
представлениями разреженных матриц.
Операция сложения алгебры многомерных матриц
Результат сложения многомерных матриц не зависит от
алгебры, которой принадлежат элементы многомерных матриц слагаемых (здесь и
далее рассматриваются алгебры, удовлетворяющие указанным выше ограничениям). На
получение элемента, не равного нулю, итоговой матрицы, не влияют элементы,
равные нулю, матриц слагаемых. Следовательно, для сложения многомерных матриц,
достаточно сложить элементы, не равные нулю. Рассмотрим осуществление сложения
многомерных матриц в иерархических структурах.
Определение
3: Иерархическим представлением матрицы 
, которая является результатом операции
сложения многомерных матриц 
и 
, назовем иерархическую структуру 
, элементы которой получаются из элементов
иерархических структур матриц слагаемых 
и 
, по формуле 
.
Рассмотрим пример.
Пример 1. Сложение двух трехмерных матриц над полем действительных
чисел
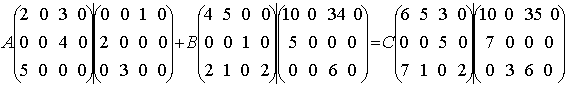
Результат сложения в иерархической структуре
представляет собой объединение всех ветвей иерархических структур слагаемых
(рис. 5).
А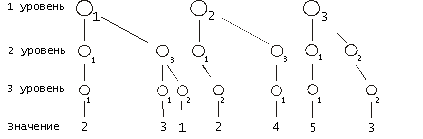
+
B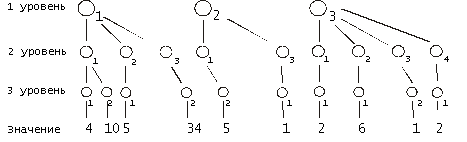
=
C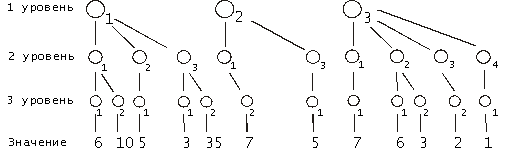
Рис. 5. Сложение в иерархических структурах
Очевидно, что при сложении иерархических структур –
представлений многомерных матриц, количество операций с элементами многомерной
матрицы значительно сокращается и зависит от степени разреженности многомерных
матриц слагаемых.
Операция умножения алгебры многомерных матриц
Аналогично сложению многомерных матриц, результат
умножения многомерных матриц зависит только от значений индексов не нулевых элементов
многомерных матриц множителей. Из определения операции умножения многомерных
матриц, следует, что элемент, не равный нулю, в итоговой матрице, имеющий набор
индексов 
(объединение групп
индексов), может получиться только тогда, когда у элементов, не равных
нулю, первой матрицы и второй совпадают
значения индексов групп 
.
Таким образом, на получение элемента, не равного нулю,
итоговой матрицы, не влияют элементы, равные нулю, матриц множителей. Следовательно,
для умножения многомерных матриц, достаточно умножить элементы, не равные нулю,
матриц множителей. Рассмотрим осуществление умножения многомерных матриц в
иерархических структурах.
Определение 4: Иерархическое
представление матрицы 
, которая является результатом операции
умножения иерархических представлений многомерных матриц 
и 
, p и q-мерных соответственно - задается
следующим образом. Разобьем совокупности индексов 
и 
на четыре
группы, содержащие соответственно k,
l, m
и n индексов (k, l,
m, n
³ 0). Причем k+l+m=p, а l+m+n=q. Обозначим группы индексов как 
, 
, 
и 
. Представим матрицы A и B в виде 
и 
. Индексы групп s и c в матрицах
A и B полностью совпадают. Тогда
иерархическим представлением матрицы 
, будет 
, элементы которого получаются из
элементов иерархических структур матриц слагаемых 
и 
, по формуле 
.
Умножение в иерархических структурах выполняется
следующим образом. Осуществляется объединение двух иерархических структур – множителей
по совпадению уровней s и c (значения перемножаются). И удаление из представления
c
уровней, сохраняя при этом связи с последующими уровнями в иерархической
структуре (при дублировании - значения суммируются) (рис. 7).
Рассмотрим пример.
Пример 2.
Умножение двух трехмерных матриц над полем действительных чисел
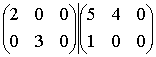
и
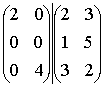
Выберем группы
индексов для умножения:
Произведением матриц 
и 
будет являться
матрица 
, элементы которой получаются по формуле: 
.
На рис. 6 показан процесс получения элементов матрицы 
.
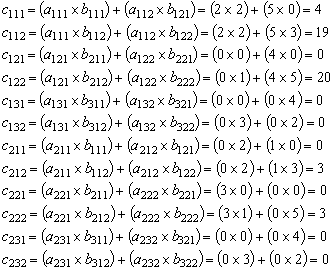
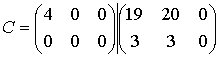
Рис. 6. Процесс умножения числовых матриц
А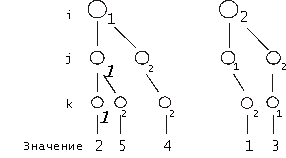
*
B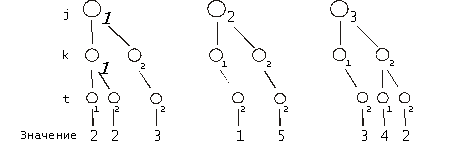 
=
C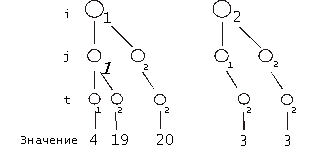 
Рис. 7. Умножение в иерархических структурах
Аналогично сложению, при умножении иерархических
структур (рис. 7) – представлений многомерных матриц, количество операций с
элементами многомерной матрицы значительно сокращается и зависит от степени
разреженности многомерных матриц множителей.
Иерархическое представление унарных
операций алгебры многомерных матриц
Сечение многомерной матрицы
Определение 5: Иерархическое
представление сечения многомерной матрицы 
где индексы
принимают
значения от 1 до 
соответственно,
по набору индексов 
, - задается следующим образом. Разобьем совокупности
индексов 
на две
группы, содержащие соответственно l
и m индексов (l, m ³ 0). Причем l+m=p. Обозначим группы индексов как, 
и 
и каждый из
индексов 
, где 
принимает
значения от 1 до l, имеет фиксированный
набор значений из соответствующего множества от 1 до 
. Тогда
иерархическим представлением матрицы 
, будет 
, элементы которого получаются из
элементов иерархической структуры матрицы 
, по формуле 
.
Свертка многомерной матрицы
Определение 6: Иерархическое
представление свертки многомерной матрицы 
где индексы
принимают
значения от 1 до 
соответственно,
по набору индексов 
, - задается следующим образом. Разобьем совокупности
индексов 
на две
группы, содержащие соответственно l
и m индексов (l, m ³ 0). Причем l+m=p. Обозначим группы индексов как, 
и 
. Тогда иерархическим
представлением свертки 
матрицы 
будет 
, элементы которого получаются из
элементов иерархической структуры матрицы 
, по формуле 
.
Транспонирование многомерной матрицы
Определение
7: Иерархическим представлением транспонирования многомерной матрицы
по индексам 
и 
, не равным между собой, будет иерархическая
структура 
, элементы которой получаются из
элементов иерархической структуры 
, по формуле 
.
6. Заключение
В статье
рассмотрена модель матричного представления информации с ее иерархической
реализацией. Можно выделить следующие основные характеристики этой модели:
- универсальность правил
структурирования данных для произвольных предметных областей и независимость их
от человеческого фактора при отображении предметной области в информационной
системе;
- наличие
объединенного математического аппарата обработки и многомерного анализа
информации, основанного на операциях алгебры многомерных матриц;
- реализация в
существующих СУБД, за счет иерархического представления алгебры многомерных матриц.
Литература
1.
Гендель
Е. Г., Мунерман В. И. Применение алгебраических моделей для синтеза процессов
обработки файлов. //Управляющие системы и машины. - Киев: Наукова думка. - № 4. - 1984.
2.
Банников
В. М., Гендель Е. Г., Мунерман В. И., Шкляр Б. Ш.. Оптимизация процессов
обработки данных на базе алгебраических моделей. //Управляющие системы и машины”.
- Киев: Наукова думка. - № 6. - 1985.
3.
Левин
Н. А., Мунерман В. И., Сергеев В. П. Алгебра многомерных матриц как универсальное
средство моделирования данных и ее реализация в современных СУБД // Системы и
средства информатики. - Москва: Наука. - Вып. 14. - С. 86-99.
4.
Сергеев
В. П. Представление многомерных матриц в иерархических
структурах для повышения эффективности хранения и процессов обработки данных // Системы и средства информатики.
Стохастические технологии и системы. (Специальный выпуск). - Москва: ИПИ РАН, 2005.
5.
Левин
Н. А., Сергеев В. П. Иерархическое представление алгебры многомерных матриц . Деп. ВИНИТИ 12.09.06. - №1149-В2006.
- 13 с.
ИПИ РАН
Поступила
в редакцию 15.06.2007.