- Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 6. -
Вып. 2. - 2007. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-14-html/TITL-14.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-14-html/cont.htm
УДК
621.396.969
Синтез адаптивного оптимального алгоритма
междупериодной обработки
эхосигналов В РЛС
на основе метода
инвариантного погружения
Ó
2007 г. С. А. Вашкевич
Для междупериодной обработки сигналов в существующих
импульсных РЛС наиболее часто применяется алгоритм быстрого преобразования
Фурье, реализующий обработку, согласованную с доплеровским спектром
эхосигналов. Альтернативой согласованной является оптимальная обработка,
выполняемая в соответствие с теорией фильтрации марковских случайных процессов.
Однако синтезированные алгоритмы оптимальной обработки не всегда оказываются
устойчивыми. Цель данной статьи заключается в разработке адаптивного
оптимального алгоритма, обладающего повышенной устойчивостью.
Одним из перспективных направлений совершенствования РЛС является оснащение их возможностью дистанционного наблюдения за облучаемыми объектами или поверхностями. Эта способность РЛС получила общее название “Радиовидение” [1]. Она позволяет независимо от времени суток и погодных условий наблюдать за объектами, находящимися на больших дальностях, в текущем времени. Особенно интенсивно это направление развивается в РЛС обзора земной (морской) поверхности, установленных на борту воздушных или космических носителей [2–4].
В настоящее время с развитием цифровых способов
обработки сигналов и возможностей специализированных вычислительных систем
появилась предпосылки к реализации этой способности и в наземных РЛС,
осуществляющих наблюдение за воздушными объектами. Она позволит существенно
повысить качественные характеристики процессов распознавания аэродинамических
объектов и разрешения групповых целей. Объекты в РЛС, обладающих способностью
радиовидения, наблюдаются на индикаторах в виде радиолокационных изображений
(РЛИ). РЛИ формируются в результате наложения откликов оптимальных фильтров,
выполняющих внутрипериодную и междупериодную обработку эхосигналов, на
двумерной плоскости в координатах наклонная дальность – доплеровская частота
или наклонная – поперечная дальности.
В качестве оптимального
фильтра по наклонной дальности наиболее часто используется фильтр,
согласованный со спектром зондирующего сигнала, а по доплеровской частоте
(поперечной дальности) – фильтр, согласованный с шириной доплеровского спектра
отраженного сигнала.
Альтернативой согласованному
фильтру по доплеровской частоте может служить оптимальный фильтр,
синтезированный на основе теории фильтрации марковских случайных процессов
[5, 6]. Однако этот оптимальный фильтр не всегда оказывается устойчивым.
Расхождение фильтра связано с отличием априорных данных, используемых при
синтезе, и параметров фазовой структуры отраженных сигналов из-за неизвестного
закона их изменения. Одним из направлений предотвращения потери устойчивости
функционирования фильтра является адаптация параметров фильтра к параметрам
отраженного сигнала. В результате фильтр становится адаптивным.
Одним из методов теории
адаптации стохастических алгоритмов является метод инвариантного погружения
[7]. В основе метода лежит минимизация функции штрафа при ненулевых граничных
условиях.
Цель статьи заключается в
разработке адаптивного алгоритма междупериодной обработки отраженного сигнала
на основе метода инвариантного погружения.
Синтез алгоритма проводится
в интересах использования его в процедуре формирования РЛИ групповых целей.
Однако этот алгоритм имеет и самостоятельное практическое значение. Он может
эффективно использоваться в стандартных алгоритмах обработки эхосигналов в РЛС
с длительным когерентным накоплением.
Синтез алгоритма целесообразно начать с выбора и аналитического описания функции штрафа. Функция штрафа составляется для расширенного вектора оцениваемых параметров, в который входят как информационные параметры, характеризующие интенсивность отражения каждой точки облучаемой поверхности, так и сопутствующие (фазовые) параметры отраженного сигнала. Качество синтезированных алгоритмов зависит от правильности выбора функции штрафа.
Рассмотрим типичную задачу оценивания параметров радиолокационного сигнала, описываемую следующими уравнениями наблюдения и сообщения.
Уравнение наблюдения для расширенного вектора оцениваемых параметров 
имеет вид
, (1)
где 
– вектор
информационных параметров; 
– вектор фазовых
параметров; 
– функциональная
зависимость, описывающая преобразование параметров расширенного вектора в
отраженный сигнал; 
– вектор шумов
наблюдения.
Уравнение
сообщения описывается следующим линейным стохастическим разностным уравнением:
, (2)
,
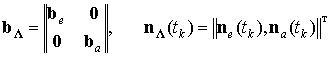где 
, 
– матрица 
переходов и вектор 
формирующих шумов
процесса 
, описывающего изменение во времени расширенного вектора оцениваемых
параметров. В частном случае, когда параметры 
не изменяются на
интервале наблюдения: 
, где 
и 
– единичная матрица и нулевой вектор
соответствующих размерностей.
Запишем апостериорную плотность вероятностей (АПВ) [8], используемую для синтеза неадаптивных алгоритмов, в общем виде
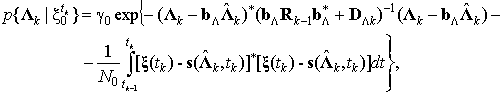(3)
где 
– матрица дисперсий
вектора формирующих шумов 
; 
– спектральная
плотность шума наблюдений; 
– нормировочная
постоянная; * – знак эрмитового сопряжения.
Известно
[7], что для любой АПВ с гауссовскими компонентами можно записать функцию
штрафа, у которой минимум достигается при значениях аргументов соответствующих
максимуму АПВ.
Рассмотрим
решение задачи формирования РЛИ групповой цели методом классического
вариационного исчисления.
Составим соответствующий АПВ (1) функционал штрафа:
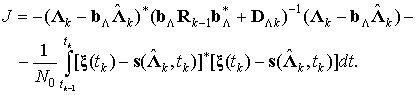(4)
Известно [7], что при решении задачи оптимизации методом классического вариационного исчисления функционал штрафа дополняется дифференциальными или разностными уравнениями, описывающими поведение системы, со специальными коэффициентами, называемыми множителями Лагранжа. Затем выделяется скалярная функция (Гамильтониан) и по ней составляются канонические уравнения как для компонентов оцениваемого вектора, так и для множителей Лагранжа. Совместное решение этих уравнений дает алгоритм оценивания параметров отраженного сигнала.
Поскольку функционал штрафа (2) записан в дискретно-непрерывной форме, то соответствующий ему гамильтониан имеет вид
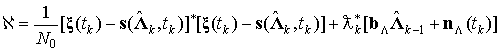, (3)
где 
– вектор множителей
Лагранжа.
Описанным образом можно эффективно решать задачи с
нулевыми граничными условиями. Получаемый в результате алгоритм идентичен
алгоритму, синтезированному на основе метода локальной гауссовой аппроксимации
[8]. Качество обоих алгоритмов одинаково, поэтому не имеет смысла подробно их
рассматривать. Другое дело, когда граничные условия оказываются ненулевыми. В
новых условиях решение в рамках метода локальной гауссовой аппроксимации
чрезвычайно затруднено или вообще не возможно. Важно то, что замена условий в
задаче оценивания методом инвариантного погружения приводит к относительной
инвариантности в выборе функциональных зависимостей, описывающих уравнение
наблюдения. В связи с чем метод синтеза алгоритмов оценивания (оценивания и
идентификации) и получил название метода инвариантного погружения. Сам метод подробно
описан в работе [7]. Синтезированные с его помощью алгоритмы имеют особенность,
которая выгодно отличает их от других алгоритмов. Особенность заключается в
том, что уравнение дисперсии зависит от невязки, в то время как сам фильтр
остается фильтром первого порядка. Благодаря которой в процессе
функционирования фильтр расходится значительно реже, чем другие при неточном
описании уравнения наблюдения или несовпадении его параметров с параметрами
входной реализации.
С учетом уравнений (1) и (2) адаптивный алгоритм формирования РЛИ групповой цели, синтезированный по методу инвариантного погружения, имеет вид
уравнение оценки:
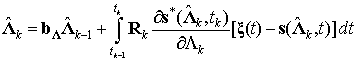; (6)
уравнение дисперсии:
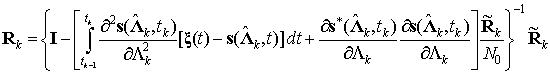, (7)
где 
– уравнение априорной
дисперсии; 
– диагональная
единичная матрица;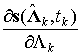 
– матрица Якоби; 
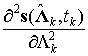– матрица Гесса.
Для частного случая
оценивания расширенного вектора, компоненты которого представлены случайными
величинами, т. е. независящими от времени на интервале наблюдения 
, алгоритм немного упрощается:
уравнение оценки
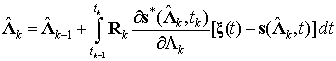; (8)
уравнение дисперсии
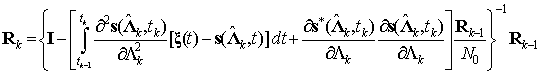. (9)
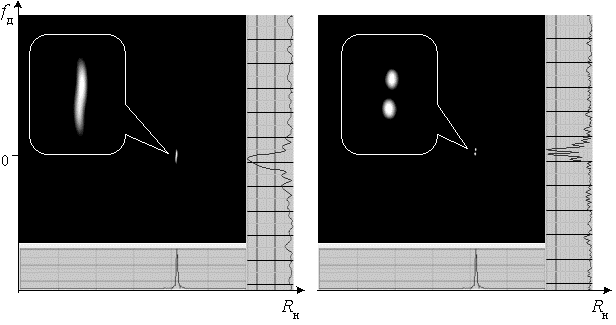
В результате
экспериментальной проверки качества функционирования разработанного алгоритма
(8), (9) получено РЛИ (рис. 1, б) групповой цели, состоящей из двух
аэродинамических объектов. Для сравнения эффективности алгоритма по улучшению
разрешающей способности РЛС приведено
РЛИ групповой цели, полученное с использованием алгоритма согласованной
междупериодной обработки (рис. 1, а).
а б
Рис. 1. РЛИ,
полученные с использованием алгоритма на основе:
а – согласованной
обработки; б – адаптивной оптимальной
обработки
Анализ двух
изображений позволяет сделать вывод, что разрешающая способность
синтезированного алгоритма значительно превосходит аналогичную способность
согласованного традиционного алгоритма гармонического анализа [3]. При увеличении
длительности когерентного накопления разрешающая способность алгоритма
согласованной обработки приближается к разрешающей способности синтезированного
алгоритма. Однако при увеличении длительности когерентного накопления возрастает
влияние фазовых флуктуаций отраженного сигнала на качество РЛИ из-за превышения
интервала когерентной обработки продолжительности интервала истинной
когерентности отраженного сигнала. Увеличить интервал когерентности можно за
счет автофокусировки [8]. Но, как показывают экспериментальные исследования,
алгоритмы автофокусировки не всегда способны эффективно функционировать при
малых отношениях сигнал-шум в условиях нестабильности параметров движения объектов
групповой цели.
Синтезированный
алгоритм выгодно отличается от алгоритмов локальной гауссовой аппроксимации по
устойчивости и качеству формируемых РЛИ при воздействии эхосигнала с широким доплеровским
спектром. Расширение доплеровского спектра связано с маневрированием групповой
цели как скоростью, так и направлением полета.
Работа
выполнена в рамках проекта № 07-07-96401 регионального конкурса «Центр»
при финансовой поддержке администрации Смоленской области и РФФИ.
Литература
1. Радиовидение / Под ред. Г. С. Кондратенкова. М., Изд-во ВВИА, 1997.
2. Радиолокационные
станции воздушной разведки / Под ред. Г. С. Кондратенкова. М.,
Сов. радио, 1980.
3. Радиолокационные
станции с цифровым синтезированием апертуры антенны / Под ред.
В. Т. Горяинова. М., Радио и связь, 1988.
4. Радиолокационные
станции обзора Земли / Под ред. Г. С. Кондратен-кова. М., Радио
и связь, 1983.
5. Ярлыков
М. С., Миронов М. А. Марковская теория оценивания случайных процессов.
М., Радио и связь, 1993.
6. Тихонов
В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических
устройств и систем. М., Радио и связь, 1991.
7. Сейдж Э. П., Мелса Д. Л. Идентификация систем управления. М., Наука, 1974.
8. Карпов О. А., Вашкевич С. А. Оптимальная адаптивная обработка сигналов в РЛС с цифровым синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА ВПВО ВС РФ, 2005.
Synthesis of adaptive optimum
algorithm between the period
of processing of
signals In radar-tracking stations on
the basis of
a method of
invariant immersing
S. A. Vashkevich
For
between the period of processing of signals in existing pulse radar-tracking
stations most algorithm FFT, realizing processing coordinated with a Doppler’s
spectrum of signals frequently is applied. Alternative coordinated is the
optimum processing which is carried out in conformity with the theory of a
filtration Markov’s of casual
processes. However synthesized algorithms of optimum processing not always
appear steady. The purpose of given clause consists in development of the
adaptive optimum algorithm having increased stability.
Кафедра радиоэлектроники
Военная академия войсковой ПВО ВС РФ
Поступила в редакцию
15.05.2007.