- Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 6. -
Вып. 3. - 2007. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-15-html/TITL-15.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-15-html/cont.htm
УДК 340.624.1
Некоторые способы количественной характеристики пули, в моделировании огнестрельного травматического процесса
Ó 2007 г. Беляев Л. В.*,
Колкутин В.В.*, Макаров И. Ю.**, Мусин Э. Х.*
В статье изложены математические показатели формы головной части снаряда, которые имеют четкие математические выражения. Проведен анализ геометрических параметров огнестрельных снарядов, которые могут влиять на морфологически особенности огнестрельного повреждения и использоваться при решении диагностических вопросов в раневой баллистике.
Ключевые слова: головная
часть снаряд, математические параметры, критические поверхности снаряда.
Моделирование огнестрельного повреждения, в частности математические способы этого, требуют определить подходы к возможностям количественной характеристики пули, найти наиболее оптимальные варианты таких количественных характеристик.
Общепринятыми и широко используемыми количественными
характеристиками огнестрельного снаряда являются ее форма, масса, скорость, энергетические
параметры. Ряд этих характеристик использовались и продолжают использоваться
практически во всех научных изысканиях по раневой баллистики, а так же в
практической экспертной работе.
На современном этапе развития научных представлений об
огнестрельном повреждении и механизмах его образования стали использоваться и математические
инструменты [1, 2, 4, 6, 7]
Результатом использования математики является
математическое моделирование, которое в наиболее полной форме позволяет описать
механизм образования огнестрельного повреждения и представить отдельные существенные
составляющие огнестрельного травматического процесса [1, 3, 4, 5].
Естественно, что пуля является важнейшей образующей
огнестрельного повреждения и для использования ее в математическом
моделировании возникает необходимость количественных характеристик ее
особенностей. Достижению этой цели и посвящена данная работа.
Используя ГОСТ 28653-90 (Термины и определения в
области понятий стрелкового оружия) определим используемую в работе
терминологию (Далее
термины, касаемо огнестрельного оружия, будут приведены согласно ГОСТУ
28653-90).
Пуля патрона (пуля) – метаемый элемент, выбрасываемый из канала
ствола стрелкового оружия.
Головная часть пули патрона
стрелкового оружия (головная часть пули)
– передняя часть пули до ведущей части пули патрона стрелкового оружия.
Вершинка пули патрона стрелкового
оружия (вершинка пули) – передний конец
пули патрона стрелкового оружия.
Ведущая часть пули патрона
стрелкового оружия (ведущая часть пули) –
цилиндрическая или коническая часть или части пули патрона стрелкового оружия,
обеспечивающая, как правило, врезывание в нарезы канала ствола, правильное
движение пули по каналу ствола и обтюрацию пороховых газов.
Хвостовая часть пули патрона
стрелкового оружия (хвостовая часть) –
нижняя часть пули патрона стрелкового оружия.
В последующем ведущая и хвостовая части пули будут
именоваться как тело снаряда; пуля – снаряд. При взаимодействии с преградой
(мишенью) снаряд при обычном (правильном) положении взаимодействует своей
головной частью, а именно с поверхностью вершинки, которая будет первичной контактной поверхностью (ПКП).
Поверхности, которые при динамическом контакте (ударе)
передают движение материальным точкам преграды, в направлении движения снаряда
и вследствие чего образуются критические давления деформации сжатия, при
которых происходит разрушение повреждаемой материи, назовем как критическими поверхностями.
Критическими поверхностями снаряда могут быть как ПКП
так и иные конструктивные элементы снаряда образующие критическую деформацию
сжатия в каждом случаи повреждения и при этом данные поверхности определяют
морфологию раны и в частности входной. ПКП может являться любая поверхность
снаряда, и она же является критической поверхностью. Например - боковая
поверхность тела снаряда в момент поражения тканей боковой проекцией.
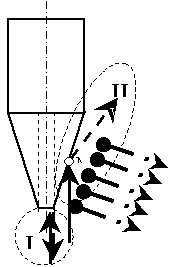
Рис. 1. Схема взаимодействия движущегося снаряда
Рассмотрим взаимодействие движущегося снаряда с биологической тканью при нормальном положении снаряда и выберем систему отсчета, при котором снаряд остается неподвижным, а движется повреждаемая ткань. Предложенная система отсчета наиболее показательна и к тому же в изучении раневой баллистики еще не использовалась (рис. 1).
Ткани при
контакте с поверхностью затупленной вершинкой (позиция I) отражаются в обратном
направлении (пунктирная стрелка), т.е. происходит деформация сжатия, при
которой скорость тканей в данных точка равна нулю, тем самым образуется
критическое давление, приводящее к разрушению тканей, т.е. образуется дефект
раневого канала. Таким образом, перед вершинкой снаряда, критической
поверхностью, образуется уплотнение тканей с критическим давлением до выходной
раны.
Ткани, контактирующие с боковой
поверхностью конусообразной головной части снаряда (позиция I) ударяются с ней под острым углом и отражаются
(пунктирная стрелка). Отражение полагаем, происходит по закону отражения, угол
падения равен углу отражения по отношению перпендикуляру касательной в данной
точке. При этом отражение происходит тканей, непосредственно контактирующих с
поверхностью снаряда, т.е. в пограничном слое. Отражение в пограничном слое
подтверждается наблюдениями в экспериментах в виде обратного выброса мелких
костных частиц. Ткани, которые непосредственно не соприкасаются с боковой
поверхностью, по законам гидродинамики смещаются перпендикулярно касательным
боковой поверхности, т.е. вперед и стороны. Полагаем, что это смещение тканей и
есть «боковое действие» снаряда.
Описанная модель не нова по своей сути, но не
использована в таком виде в изучении раневой баллистике. Образование скачка
давления (сопротивления) на поверхности вершинки головной части снаряда
наглядно показана в работах по изучению распределения давления на поверхностях
головных частей огнестрельных снарядов [8] (рис. 2).
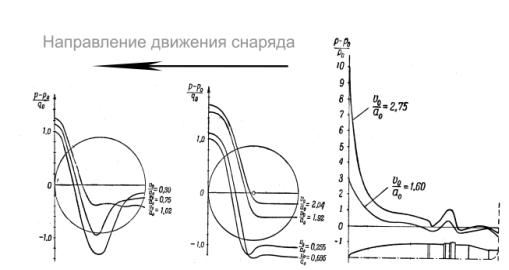
Рис. 2. Распределение давления на поверхностях снарядов
Скорости снарядов приведенные в числе Маха (отношение
скорости огнестрельного снаряда к скорости звука в воздухе, М 1,0 = 340 м/с).
При скоростях 102–346,8 м/с (М0,33-М1,02) на головной
части сферического снаряда наибольшее давление оказывается на передней
поверхности, вершинки снаряда. При скоростях свыше скорости звука – 652,8-693,7
м/с (1,92-2,04) давление занимает большую площадь головной части, для наглядности
показано распределение давление при скоростях 86,7-236,3 м/с (0,255-0,695).
На снарядах сигарообразной формы наибольшее давление
воздуха располагается в головной части показанные при скоростях 544-935м/с (1,6-2,75)
и быстро снижается к телу снаряда.
Распределение давления (сопротивления) воздуха на
поверхности головной части снарядов различной формы при разных скоростях имеет
корреляцию с морфологическими проявлениями повреждений на биологических
преградах, данный факт в последующем будет, упомянут при анализе морфометрических
особенностей входных огнестрельных повреждений.
Из данного анализа выводятся два вывода:
а) критические давления образуются на поверхностях
снаряда, отражающие ткани в направлении полета снаряда и тем самым происходит
их разрушение.
б) так называемое боковое действие образует не тело
снаряда, боковая поверхность конической формы головной части снаряда.
Надо полагать, что одним из факторов влияющих на объем
повреждений является геометрические и размерные параметры головной части снаряда
влияющие на объемы образование дефектов и образование боковое смещение ткани.
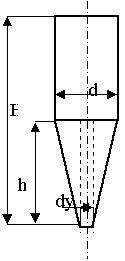
Рис. 3. Размерно-геометрические параметры снарядов: Н-
длина снаряда, h – высота головной части, d – диаметр тела, dy – диаметр вершинки
Измерения производились штангенциркулем в поле зрения
микроскопа с увеличением до 24х с вычислением среднего значения. Так
как вершинка не имеет четких границ сопряжения (ребра) с боковой поверхностью,
диаметр вершинки определяли по касательной образующейся при угле 90 градусов к
осевой линии, как на остроконечных, так и тупоконечных пулях.
Измерения проводили 12 снарядов и определяли по
общеизвестным формулам: площади поперечного сечения тела (Sd), ударника (Sу);
объемов – общего (U), головной части
(Uг), тела (Uт).
На основании полученных результатов были вычислены
соотношения головной части к диаметру – показатель длины головной части (во
сколько раз длина головной части больше диаметра ведущей части снаряда); и диаметра
тела к диаметру ударной поверхности – показатель «затупления» головной части
(при наименьшем затуплении показатель стремится к нулю, при цилиндрической
форме показатель равен 1).
Эмпирическим путем установлено, что величина отношения
коэффициента «затупления» к коэффициенту длины головной части, имеет корреляцию
с формой снарядов по их обтекаемости (по форме и длине головной части), т.е.
данный коэффициент может характеризовать способность снаряда преодолевать
сопротивление среды прохождения.
Таблица расчетов геометрических параметров снарядов ручного огнестрельного оружия
|
Патроны Математические показатели снаряда |
5,45-мм
(5,45х39) |
5,45-мм МПЦ |
7,62-мм
(7,62х39) |
7,62-мм
Винт |
7,62-мм ТТ |
7,62-мм
рев. |
7,65-мм Браунинг |
СП-4 |
9-мм ПМ |
СП-5 |
СП-6 |
11-мм CAP |
|
Показатель длины головной части (H/d) |
2,32 |
1,16 |
1,82 |
1,81 |
0,77 |
0,82 |
0,77 |
0,1 |
0,58 |
1,61 |
1,61 |
0,74 |
|
Показатель затупления (d/dу) |
0,27 |
0,38 |
0,19 |
0,19 |
0,51 |
0,51 |
0,51 |
0,77 |
0,6 |
0,11 |
0,11 |
0,57 |
|
Математический показатель формы головной части |
0,3 |
0,12 |
0,2 |
0,2 |
0,34 |
0,31 |
0,34 |
46,2 |
0,62 |
0,72 |
0,72 |
0,44 |
Таким образом, данный математический показатель формы
головной части снаряда имеет четкое математическое выражение, способ своего
расчета. Предварительное использование этого показателя в математических моделях
дало существенный информационный результат, который будет опубликован в
последующих работах.
Литература
1.
Беляев Л. В. Использование количественной характеристики копоти для уточнения
дистанции близкого выстрела / Л.В. Беляев // Суд.-мед. эксперт. – 1985. – № 3.
– С. 17-19.
2.
Гальцев Ю. В. Характер и особенности огнестрельных переломов диафизов бедренных костей человека в зависимости
от скорости полета пули / Ю. В. Гальцев // Актуальные вопросы теории и
практики судебной медицины. – Л., 1986.– С. 52-54.
3.
Емелин А. И. Об унификации описания огнестрельных снарядов / А. И. Емелин //
Суд.-мед. эксперт. – 1996. – № 4. – С. 10.
4.
Колкутин В. В. Использование биологических и небиологических имитаторов для
моделирования огнестрельных повреждений различных органов и тканей / В.В.
Колкутин // Методические рекомендации, тема № 25-93-в5. – СПб.: ВМедА, 1993. –
15 с.
5. Кузнецов Ю. Д. Диагностика повреждений выстрелом из
самодельного огнестрельного оружия / Ю.Д. Кузнецов // Суд.-мед. эксперт.–1985.–
№ 3.–С. 16-17.
6.
Лисицын А. Ф. Огнестрельные повреждения из охотничьего оружия в судебно-медицинской
практике. - Дисс... докт... наук, Л., 1974.
7.
Попов В. Л. Пути решения судебно-медицинской проблемы установления расстояния
выстрела и взрыва в пределах неблизкой дистанции / В.Л. Попов // Актуальные
вопросы теории и практики судебно-медицинской экспертизы. – Л., 1982. – С.
61-62.
8.
Окунев Б. Н. Основы баллистики /
Б.Н.Окунев // Воен.Издат.- М., 1949. - Том. 1, кн.1.
Some ways of the quantitative characteristic of a
bullet, In modelling fire traumatic process
Kolkutin V. V., Belyaev
L. V., Makarov I. J., Musin E. H.
In article mathematical parameters of the form of a head part of a shell
which have precise mathematical expressions are stated. The analysis of geometrical
parameters of fire shells which can influence morphological features of fire
damage is lead and be used at the decision of diagnostic questions in wound ballistics.
Key words: a head part a shell, mathematical parameters, critical surfaces of a
shell.
* 111 Главный
государственный центр судебно-медицинских и криминалистических экспертиз
Министерства обороны
Российской Федерации
** Кафедра судебной медицины
Военно-медицинская академия
Поступила в редакцию
30.06.2007.