- Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 6. -
Вып. 3. - 2007. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-15-html/TITL-15.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-15-html/cont.htm
ПИСЬМА В
РЕДАКЦИЮ
УДК 57.01
О математизации биологии
Ó 2007 г. Седова
Г. П.
Язык природы есть язык математики
Г. Галилей
В
настоящее время биология подошла к такому рубежу, когда традиционные ее отрасли,
такие как зоология, ботаника, анатомия и другие становятся все менее продуктивными,
и мало что могут дать для ее дальнейшего
развития. Описательный период в биологии заканчивается. В основном
все биологические объекты описаны и
систематизированы. Образно говоря, пройдя в своем развитии период детства и
юности, биология вступает в свое
взрослое, зрелое состояние.
А зрелость любой науки о
природе характеризуется тем, что ее основные законы выражены в математической
форме. Понятно, что процесс этот долгий и непростой, но биология должна
стремиться к этому для того, чтобы превратиться в точную науку.
Как
известно, математика – это наука о количественных соотношениях и пространственных
формах реального мира. Наука эта абстрактная, для нее нет разницы с объектами
какой природы она имеет дело. Поэтому от математики бесполезно ждать конкретных
результатов, проясняющих суть того или иного биологического процесса.
Математика исследует только соотношения между величинами. Хорошо выразил эту
мысль академик Н. П. Дубинин: «Математика является лишь методом, который отнюдь
не компетентен в деле обнаружения самой
сущности явления» [Дубинин Н. П. «Вечное
движение»].
У биолога естественно
возникает вопрос: зачем тогда применять математику, если она все равно не может
раскрыть сущность того или иного биологического явления?
Да, сущность явления она не
раскроет, но найдет соотношения, закономерности, которые может не обнаружить
биолог. Тем самым будет указано направление, в котором нужно
экспериментировать, чтобы проникнуть в суть
явления.
Считаю, что наиболее простой
биологической проблемой, поддающейся математизации, и как оказалось легко
решаемой, является проблема количественного нарастания массы живых организмов.
Эта проблема является пограничной между математикой и биологией. Она допускает
математическую постановку задачи, а именно:
Перед нами имеются
полученные экспериментальным путем числовые таблицы, показывающие как нарастает
масса того или иного организма в зависимости от времени.
Известно также, что масса
живого организма нарастает путем удвоения составляющих ее элементов. «Клетка от
клетки» - это закон биологии, не знающий исключений. Еще никто не наблюдал
такого явления, чтобы клетка образовалась в единственном числе из составляющих
ее веществ. Содержимое клетки также растет путем удвоения. В процессе роста в
клетке удваиваются органеллы и все ее cоставные части. Т. е., все
живое растет путем удвоения своей массы.
То, что рост любого живого
организма замедляется с течением времени это повседневно наблюдаемый факт.
Переводя на язык математики, это означает, что период удвоения массы живого
организма с течением времени увеличивается. Но есть ли какой-либо закон в этом
увеличении?
Если подойти к этому вопросу
чисто умозрительно, то трудно предположить, что таким сложным процессом, как
рост живого, управляет простой закон. Ведь сколько разных причин, помимо
фактора времени, влияет на этот
процесс. Реально предположить корреляционную зависимость от времени,
т.е. зависимость есть, но осложнена другими факторами.
Вернемся к поставленной
задаче. Имея экспериментальные таблицы зависимости массы живых организмов от
времени, вычислим соответствующие каждому моменту времени t периоды
удвоения массы по формуле:
![]()
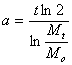
![]()
Нанесем полученные значения на график a =¦ (t). И неожиданно для себя мы получаем почти идеальную прямую
линию (за исключением нескольких первых точек и этому есть объяснение).
Уравнение прямой линии
записывается следующим образом:
a= ao + k t (1)
Вот по такому простому
закону изменяется период удвоения массы. А сама масса биологического объекта
выражается следующей формулой
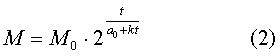
Более подробно вывод формул (1) и (2) рассмотрен в моей
статье «Закономерность роста биологических объектов», напечатанной в журнале
«Математическая морфология» за 2004 г. [http://www.smolensk.ru/user/sgma/MMORPH/N-10-html/sedova/Sedova2004.htm].
Итак, графики нам показали, что основная закономерность, управляющая
ростом живой материи – линейный закон увеличения периода ее удвоения в функции
от времени. Все же остальные факторы, влияющие на рост, основного значения не
имеют, они определяют небольшие колебания, сопровождающие рост на всем его
протяжении.
Основатель теории роста
академик И. И. Шмальгаузен писал: «В основе стремления понять рост как целое
лежит, очевидно, мысль, что весь процесс управляется внутренней
закономерностью, прямо определяющей его
течение… ряд таких влияний, как рождение, смена питания при окончании
лактации, гормональные влияния, например, при наступлении половой зрелости и
т.п. оказывает отчетливо нарушающее рост воздействие. Само собой разумеется,
что эти воздействия ничего общего не имеют с внутренними закономерностями роста
и мы, следовательно, не можем допускать, чтобы они вовлекались в формулы роста,
если хотим, чтобы последние правильно выражали внутренние закономерности
процесса роста. Если мы свалим в кучу все эти гетерогенные процессы, то даже
самая лучшая математическая обработка кривых роста не продвинет нас ни на шаг
вперед. Она останется только простым
описанием сложного явления, и если бы даже дала точные результаты, то не могла
бы принести никаких перспектив для дальнейшего проникновения в природу самого явления».
Возникает вполне законный
вопрос:
Как можно результат,
полученный на отдельных биологических объектах (организмах, органах, тканях и
пр.) распространять на весь живой мир и делать такой обобщающий вывод?
Дело в том, что в биологии
нельзя применить метод математической
индукции, позволяющий доказать справедливость какого-либо утверждения в
общем виде, если оно справедливо для нескольких значений. Нельзя в биологии
применить и метод от противного. Единственным критерием справедливости того или
иного утверждения в биологии может быть только соответствие его эксперименту, и
чем на большем количестве биологических объектов оно проверено, тем больше
уверенность в том, что это утверждение имеет всеобщий характер.
В данном случае
справедливость формулы (1) проверена мною на взятых из литературы
экспериментальных данных по росту следующих объектов:
Эмбриональный рост - 16 разных организмов (человек,
курица, крупный рогатый скот разных пород, овца, свиньи разных пород, буйвол,
верблюд, кролик, морская свинка, крыса белая, домашняя, мышь домашняя, белая,
личинки аксолотля, форель, перепел, чибис, малый песочник).
Постэмбриональный рост - 15
разных организмов (крупный рогатый скот – быки
и телки разных
пород, овца, свинья, кролик, морская свинка, курица, индюшка, серая куропатка,
сизый голубь, мышь домашняя, лабораторная; крыса домашняя, белая, норвежская;
лошадь першеронская, козлотур; рыбы - лещ, карп, тугун, севрюга).
Рост
отдельных частей тела, органов и тканей - 13 разных объектов (рост передней и задней конечностей
цыпленка, рост сердца, печени, селезенки, легкого, желудка, глаза, хрусталика
глаза, мозга, стенок мозга цыпленка, рост спинного мозга кур, рост почек сороки
и серой вороны).
Рост одноклеточных - 3 (парамеция,
дрожжевая клетка, бактерия micrococcus).
Рост растений - 3 (озимая
пшеница, рост соцветий астр, рост древесины
ели ситхинской).
Набухание семян растений -
10 партий семян различных растений (кукуруза, пшеница, рис, просо, сорго, горох,
овес, рожь, красный клевер, бальзамин садовый).
Все экспериментальные данные
академика И. И. Шмальгаузена, включая рост таких мелких объектов, как хрусталик
глаза цыпленка, бактерии, соответствуют формуле (1).
Думаю, что приведенных
примеров достаточно для вывода о том, что
формула (1) является универсальной формулой, характеризующей процесс
роста самых разных биологических объектов. Слишком маловероятно предположение о
том, что будет найден живой организм, растущий по иному закону. Ведь живая
природа единообразна.
Что касается коэффициентов ao и k в формуле (1) то их общий
смысл таков: ao - начальный период удвоения массы, k - коэффициент замедления роста. Более конкретный биологический смысл
этих коэффициентов путем математических рассуждений, конечно, определить
нельзя. Здесь необходимы целенаправленные эксперименты.
Осмысление формулы (1)
приводит нас к важным выводам.
Живая материя для того,
чтобы существовать, должна противостоять своему неизбежному распаду. В живом
организме все время отмирает огромное количество клеток и их необходимо
замещать новыми. В каждой клетке также происходит процесс распада.
В начале роста живого
организма энергии его роста хватает не только на то, чтобы противодействовать
этому распаду, но и на то, чтобы увеличивать свою массу. Но это увеличение
происходит все медленнее. По достижении предельного размера энергии роста
хватает только на то, чтобы противостоять распаду, возмещая отмирающие клетки.
Энергия роста продолжает уменьшаться
(это находит свое выражение в дальнейшем увеличении периода a ), поэтому
возмещение отмирающих элементов становится все менее и менее эффективным.
Отсюда ошибки, сбои в этом сложном процессе, снижение иммунитета и все прочие
явления, сопровождающие старение организма. Исследователями не обнаружено
никаких особых, свойственных старческому организму биохимических процессов по
причине того, что их нет. В старческом организме протекают все те же процессы,
что и в молодом, но их темп все более и
более замедляется.
И наконец, наступает момент, когда темп этот снижается настолько,
что организм не в состоянии поддерживать свое существование, масса его уменьшается, период ее удвоения слишком
велик, чтобы возмещать отмирающие элементы. Это определяет предел продолжительности
жизни живого организма.
Казалось бы, все элементарно
просто. Но мои попытки напечатать свою
работу в каком-либо научном журнале в течение многих лет были безрезультатны.
Приведу несколько выдержек из полученных мною рецензий для того, чтобы
показать, что основным препятствием для внедрения математики в биологию
является не сложность самого этого процесса , а отсутствие у большинства
биологов строгого математического мышления.
Вот выдержка из рецензии журнала «Биофизика» за 1992 г.: «Работа примитивная, хотя все понятно и можно напечатать».
Но напечатана, конечно, не была. Обвинений в примитивности не принимаю, нет
моей вины в том, что данная проблема оказалась так просто решаемой, что для
этого не потребовались ни дифференциальные уравнения, ни столь модное сейчас моделирование,
которое применяется иногда и там, где без него можно обойтись.
Думаю, что искусственно
усложнять проблему не стоит. В
конечном счете, мир, в том числе
и живой, устроен просто. Может быть, сложность многих теорий естествознания
объясняется тем, что мы еще не дошли до этой простоты. «Природа проста и не роскошествует
излишними причинами», - писал И. Ньютон в своем труде «Математические начала
натуральной философии».
Далее. Журнал
«Сельскохозяйственная биология». После рецензии, в которой работа оценена
хорошо и даны некоторые рекомендации по ее оформлению, получила вторую. В ней
работа названа «схоластической». «Биологии, как науке, нужен более
содержательный подход». Возражаю. Математика – наука абстрактная, но не
схоластическая. Думаю, что и с содержанием у меня все в порядке. Цитирую
дальше. «Предложена формула, аналогичная описанию роста популяции клеток, с
периодом генерации, зависящем от возраста. К сожалению, биологические механизмы
роста в статье практически не
затронуты».
Я изначально никакой формулы
не предлагала. Вид формулы получился сам собой, когда величины, вычисленные на
основании экспериментальных данных, были нанесены на график. Моя заслуга только
в том, что я выявила эту зависимость, чего, уж извините за вынужденную нескромность,
до меня сделано не было. А если бы я
еще открыла и биологические механизмы
этой зависимости, то после меня по теме роста уже делать было бы нечего.
Далее было мое обращение в
издающийся в Берлине «JORNAL OF MATHEMATICAL BIOLOGY». Рецензент профессор Берлинского университета O. Diekmann: «Никаких теоретических
новшеств мы не усмотрели. Ваша формула базируется на уже устаревших механизмах».
Возражение. Никаких
«механизмов» я в своей работе не применяла. А такой механизм, как анализ
графиков, полученных в результате экспериментов, никогда не устареет, он не
подвержен моде, также как никогда не устареют элементарные математические истины.
Что касается новшеств, то на рецензента
не произвела никакого впечатления линейная зависимость, видимо для него все
едино, что линейная, что любая другая зависимость.
После всех этих неудачных
попыток в 1998 г. я обратилась в отделение общей биологии РАН с просьбой
апробировать мою работу. Она была направлена на отзыв доктору биологических
наук профессору А. И. Зотину, главному специалисту по росту живых организмов,
автору сборника «Количественные аспекты роста организмов». Цитирую выдержку из
этой рецензии: Речь идет о
формуле
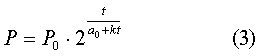
(в первой работе я вместо понятия масса организма
употребляла понятие вес организма, для биологии эти понятия равнозначны). «Это,
конечно, не формула роста, а функциональная зависимость веса от времени, написанная
в самом общем виде. Формула роста
Седовой удовлетворяет этой зависимости, но сама по себе функциональная
зависимость не является формулой роста в конкретном понимании».
Трудно понять, что здесь
хотел сказать автор рецензии. А ведь речь идет о самых элементарных
математических понятиях. Функциональная зависимость или функция - это
зависимость, показывающая, как изменяется одна величина с изменением другой
величины. Эта зависимость может быть
выражена в виде формулы, таблицы или графика.
Если выражение (3) не формула, то что же это такое?
Формула получена в общем
виде. Так это хорошо, это свидетельствует о том, что количественное нарастание
массы всех биологических объектов идет по одному и тому же закону, отличаясь
друг от друга только двумя параметрами ao и k.
Эти параметры - постоянные
для данного объекта, но разные для разных объектов.
Далее в рецензии идет речь о
формуле
a=ao
+ kt.
«Подобного рода утверждения должны быть подтверждены
экспериментальными данными. Другими словами, автору следовало бы получить или
найти в литературе данные, подтверждающие
формулу (2)».
Что здесь можно сказать?
Какими экспериментальными данными я
должна подтверждать свою формулу, если я ее вывела из этих самых экспериментальных данных, а не из
собственной головы?
Конечно, все мои возражения
мысленные, ни с какими рецензентами я в переписку не вступала, считая это
бесполезным. И привожу это здесь для того, чтобы показать, как трудно
объясняться с биологами даже на языке элементарной математики и логики.
Я, ни в коей мере не хочу
сказать, что все биологи не знают математики. В биологии есть такие примеры,
когда в одном лице сочетались знания и биологии и математики. Таким ученым был
академик И. И. Шмальгаузен, который был блестящим экспериментатором, и
одновременно внедрял математические методы в биологию.
Работой биолого-математического направления является
монография академика Н. М. Эмануэля
«Кинетика экспериментальных опухолевых процессов». Но такие примеры
немногочисленны. В основном биология остается
еще чисто описательной наукой.
До некоторых пор в России не
было журнала пограничного направления между математикой и биологией. Биологи не
знают математики, математики знают только чистую математику и не хотят особенно
глубоко вникать в биологию. И только
создание электронного журнала «Математическая морфология» исправило эту
ситуацию и дало возможность высказаться тем, кто работает в этом направлении.
Как автор нескольких статей именно такого
пограничного направления, я благодарна редактору журнала В. А.
Глотову за воплощение в жизнь идеи
создания такого журнала, благодарна членам
редакционного совета и всем тем, кто причастен к созданию этого журнала.
В заключительной части своей
статьи я коснусь темы злокачественного роста в плане того, как представляется
этот рост с точки зрения полученной
формулы нормального роста.
Опираюсь на монографию
академика Н. М. Эмануэля «Кинетика экспериментальных опухолевых процессов». В
ней автором собраны взятые из литературы данные по количественному росту 20-ти
различных опухолей. Вывод, к которому пришел Н. М. Эмануэль на основании
анализа этих данных следующий – злокачественная опухоль в начале своего
развития растет по экспоненциальному закону.
Экспоненциальный характер
роста означает, что опухоль удваивает
свою массу с постоянным периодом. Сопоставим этот результат с формулой (1)
a = ao
+ k t
Мы видим, что такой характер роста возможен только в
том случае, если слагаемое k t с некоторого момента t 1 не будет увеличиваться,
тогда величина a станет
постоянной
a =a o + k t! = const
Для старого организма период a
является большой величиной, но главное то, что начиная с момента t 1 он больше не будет увеличиваться.
Итак, злокачественный рост в
начале своего развития - это экспоненциальный рост. По такому же
экспоненциальному закону растет и популяция свободно живущих одноклеточных организмов. Общая
закономерность роста этих двух биологических
объектов дает основание представить раковую
опухоль как популяцию не связанных между собой клеток многоклеточного организма. А сам многоклеточный организм
является для этой популяции лишь
питательной средой, из которой опухоль, прорастая в нее, поглощает питательные вещества.
Зададим следующий вопрос.
Что дало возможность клетке получить
самостоятельность и образовать популяцию раковых клеток? Здесь я ссылаюсь
на свою статью «Анализ причины замедления роста многоклеточных организмов», напечатанную в журнале «Математическая
морфология» в 2005 г. [http://www.smolensk.ru/user/sgma/MMORPH/N-11-html/sedova-2/sedova-2.htm]. Суть этой работы состоит в следующем.
Анализ графиков, полученных
на основе экспериментальных данных
показывает, что потенциал роста или способность к удвоению массы в многоклеточном
организме уменьшается с увеличением его массы, причем основное падение
потенциала происходит в самом начале роста, когда масса организма очень мала.
Такого рода графики
характерны для того случая, когда объекты связаны между собой силами,
действующими на коротком расстоянии от каждого
объекта. Пример - поведение нуклонов в атомном ядре, когда каждый нуклон взаимодействует только с теми нуклонами,
которые находятся в непосредственной близости от него.
Характер приведенных в
статье графиков для разных многоклеточных
организмов дает основание утверждать, что каждая клетка многоклеточного организма испытывает на себе тормозящее рост
действие только со стороны тех клеток,
которые находятся в непосредственной близости от нее. Назовем эту область областью короткодействия. Такая
область окружает каждую клетку
многоклеточного организма. Через пересечение этих областей осуществляется
тормозящее рост действие клеток друг на друга.
А теперь представим себе
ситуацию, когда в силу каких-то причин одна из клеток многоклеточного организма
вместе со своей областью короткодействия оказалась в полной пространственной
изоляции от соседних клеток, т.е. их области короткодействия не пересекаются.
Такая клетка, освободившись от тормозящего рост действия соседних клеток,
получает возможность реализовать
сохранившийся в ней потенциал роста и начать бесконтрольно размножаться. Какой-то потенциал роста, хотя
и небольшой, имеется и у клеток
старческого организма. Поэтому злокачественный рост возможен в любом возрасте.
Представленная гипотеза
хорошо объясняет установленные исследователями злокачественного роста следующие
факты.
1. В злокачественных клетках
нет никаких принципиальных биохмических отличий, т.е. не протекает каких-либо
биохимических реакций или процессов,
которые не протекали бы в нормальных клетках (В. С. Шапот).
2. Генетический код раковой
клетки идентичен генетическому коду нормальной
клетки, о чем свидетельствуют эксперименты по замене ядер яйцеклеток ядрами, взятыми из опухоли. В
результате такой замены из яйцеклеток получалось нормальное потомство (Р. К.
Маккинз и др.).
Указанных отличий нет по
простой причине, что клетка, давшая начало
злокачественному росту, это обычная нормальная клетка, оказавшаяся
в полной изоляции от соседних клеток.
Нарушена не клетка, а механизм, передающий ей торможение от соседних клеток.
Тот факт, что злокачественный рост
поражает только многоклеточные организмы, а одноклеточные организмы не
подвержены злокачественному перерождению, говорит о том, что эта патология связана не с клетками, а с их
взаимодействием.
Развиваем мысль дальше и
задаем себе вопрос. По какой причине
клетка может оказаться в полной изоляции от соседних клеток?
Логически рассуждая, таких
причин может быть 2.
Первая причина связана с
нарушениями в ближайшем окружении
клетки. Это отмирание соседних клеток, разрушение межклеточного вещества,
пространственный сдвиг и пр. Факторов, провоцирующих эти процессы, очень много.
Вторая возможная причина –
это уменьшение радиуса короткодействия
самой клетки, может быть, даже до размеров самой клетки.
Вытекающее из упомянутых
выше графиков, общее схематичное представление о живом организме, как о системе
клеток, связанных между собой короткодействующими силами,
тормозящими рост каждой
клетки, вызывает аналогию с гипотезой клеточных биологических полей А.
Г. Гурвича.
Коротко суть ее состоит в
следующем. С каждой живой клеткой связано биологическое поле, не сводящееся ни
к одному из известных полей, выходящее за пределы клетки. Источник этого поля
находится в ядре. Объединением этих полей образуются биологические поля тканей,
органов, и, в конечном счете, биологическое поле всего организма.
Если заменить в предыдущих
рассуждениях о причине злокачественного роста понятие области короткодействия
на понятие клеточного биологического поля (что, по–видимому, одно и тоже), то
причину злокачественного роста,
согласно изложенной гипотезе, можно сформулировать следующим образом.
Клетка, положившая начало
злокачественному росту, это клетка, отделившаяся своим биологическим полем от
биологических полей соседних клеток и,
в конечном счете, от биологического поля всего организма, и по этой причине получившая возможность самостоятельного
роста.
Вообще, понятие клеточного
биологического поля давно необходимо
биологии. Иначе как можно объяснить, что живой организм, состоящий
во многом из мягких, нежных тканей,
клетки которых к тому же еще и подвижны, сохраняет свою форму неизменной во
всех жизненных ситуациях? Как вообще
существует такое огромное скопление клеток? Неужели все это может держаться на
адгезии и межклеточных контактах?
Ясно, что должен быть
какой–то невидимый каркас, определяющий
каждой клетке ее место в этом сложном сооружении.
А как можно объяснить такое
всем известное явление, когда нежная
шляпка гриба поднимает асфальт?
Или такое явление, когда
прорастающие семена растений поднимают
тяжелый груз? Так в опытах английского естествоиспытателя 18–го в. Стефана Гельса разбухающие семена гороха,
помещенные в небольшом чугунке, поднимали крышку с грузом до 80–ти кг. Ясно,
что без посредника это произойти не может. А таким посредником может быть
только биологическое поле.
«В философских построениях
крепко упрочилось представление об отсутствии резкой грани между живой и косной
материей… В науке не поставлен до сих пор прямой вопрос о причинах коренного
различия между живым и мертвым
веществом, и наоборот, считается научно правильным исходить во всей работе в этой области из постоянно
опровергаемого научным опытом
представления о том, что нет в природных процессах резкого отличия между живой и косной материей. Живое не получено
из мертвого, и нет ни малейшего успеха, никакого достижения в этих исканиях».
«Одним из первых вопросов,
стоящих перед нами в этой области, является вопрос о том, имеем ли мы дело с
обычными формами энергии, или же есть в
живом веществе новые формы энергии, отсутствующие в мертвой материи.
Впервые, кажется, Оствальд
высказал это мнение, причем он предположил, что эта особая форма энергии
объясняет и само явление жизни, в частности сознание» [В.И. Вернадский «Живое
вещество»].
Элементарной единицей живой
материи является клетка. Подавляющее
большинство органических веществ, за незначительным исключением, - производные
живой клетки. ДНК вне клетки - это просто химическое соединение, и только в
условиях клетки она выполняет свою функцию.
«Изолированная молекула ДНК,
как и любая другая мертва и ни одним
свойством живого не обладает. Как скрипка не может породить мелодию, пока
не попадет в руки виртуоза, так и молекула ДНК, тая в себе замысловатое и неповторимое сочетание нуклеотидов, сама
по себе не способна ни к самоудвоению,
ни к выдаче информации, пока не окажется в условиях клетки» [А. М. Кузин
«Вечерние раздумья»].
Хлорофилл вне растительной
клетки не осуществляет фотосинтеза. Этот процесс успешно идет в хлоропластах -
крохотных органеллах, наполненных хлорофиллом и расположенных в каждой зеленой
клетке растения.
Эти и другие факты приводят
нас к выводу о том, что с живой клеткой
связано особое состояние материи - клеточное биологическое поле, не сводимое
ни к каким известным физическим полям.
Известно, какую негативную
реакцию вызывает понятие биополя у некоторых физиков. Здесь и обвинение в
невежестве, витализме и пр. А порой
просто ничем не аргументированное отрицание этого понятия.
И позволительно спросить у
таких физиков. Разве все познано в окружающем нас мире? Много ли мы знаем о той
субстанции, которая заполняет в атоме огромное пространство между ядром и
электронной оболочкой, о той непустой
пустоте, из которой, если иметь в виду соотношение размеров, в сущности и состоит весь мир? Не имеет значения
как ее назвать - мировым эфиром,
физическим вакуумом или пространством, наделенным материальными свойствами. Да
о ней науке почти ничего не известно. А, может быть, особым состоянием этой
среды и объясняется отличие живого от мертвого?
Понятие клеточного
биологического поля биологии необходимо. Как можно без него подойти к такой
сложной проблеме, какой является морфогенез, или формообразование, т.е.
объяснить, как из зиготы образуется организм, имеющий сложную форму? Понятно,
что генетика здесь бессильна. Отсутствие такого понятия, как клеточное
биологическое поле тормозит вхождение
биологии в число точных наук.
г. Орел
Поступила в редакцию 1.08.2007.