- Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 6. -

Вып. 4. - 2007. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/TITL-16.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/cont.htm

УДК 338.945

ПРОБЛЕМЫ ВЫСОКОТЕМПЕРАТУРНОЙ СВЕРХПРОВОДИМОСТИ

Ó 2007 г. Лобачев В. В.*, Яржемский В. Г.*, Холманский А.С.**

(kholmanskiy.doc)

В работе дан краткий обзор теорий сверхпроводимости и проанализированы проблемы высокотемпературной сверхпроводимости.

ВВЕДЕНИЕ

Явление сверхпроводимости (1911 г.) было открыто через три года после того, как был получен жидкий гелий. При нормальных давлениях гелий становится жидким при температуре ~ 4.2 К. Голландский физик К. Камерлинг-Оннес обнаружил, что при столь низких температурах электрическое сопротивление некоторых металлов скачком обращается в нуль [1].

Образец металла подключается к источнику напряжения и охлаждался жидким гелием. Падение напряжения на образце, измеряемое вольтметром, при понижении температуры ниже некоторой критической Т_к обращалось в нуль. В альтернативном варианте кольцо из сверхпроводника помещалось в перпендикулярное его плоскости магнитное поле. После выключения магнитного поля в кольце возбуждался индукционный ток. В обычных металлах этот ток быстро затухает. В сверхпроводнике же ток остается и течет бесконечно долгое время. В настоящее время тонкие эксперименты показывают, что удельное сопротивление сверхпроводника, по крайней мере, не выше . Эта величина в меньше удельного сопротивления хорошего проводника – меди. Оценим время затухания сверхпроводящего тока.

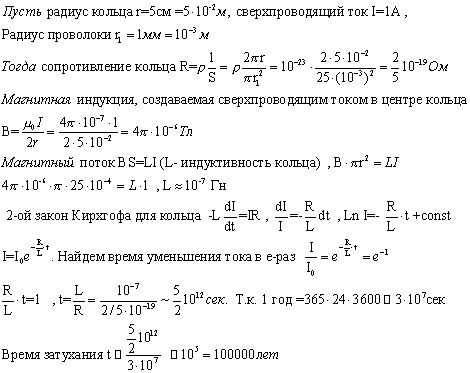
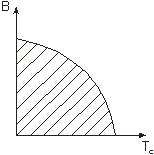
Рис. 1. Связь между В и Т_к.

Позже было обнаружено, что сверхпроводящее состояние разрушается не только при повышении температуры выше некоторой Т_к, но также и при предельных значениях магнитного поля и сверхпроводящего тока (В_к и I_к). На рис. 1 представлена примерная связь между .

СВЕРХПРОВОДНИК И ИДЕАЛЬНЫЙ ПРОВОДНИК

Поскольку сверхпроводник имеет сопротивление весьма близкое к нулю, то долгое время считалось, что свойства идеального проводника (R=0) и сверхпроводника одинаковы. Но оказалось – это справедливо только в отношении электрического сопротивления. В магнитном поле обнаруживается различие между соответствующими образцами. Возьмем идеальный проводник при температуре меньше Т_c. При внесении его в магнитное поле нулевой магнитный поток останется по-прежнему нулевым, поскольку в образце возникают вихревые токи компенсирующие увеличение внешнего магнитного потока (следовательно и магнитная индукция В=0). Если же включить магнитное поле при температуре выше критической, затем охладить образец, то в этом случае магнитное поле в идеальном проводнике останется. Возникающие вихревые токи не дадут ему измениться.

В сверхпроводнике, как обнаружили Мейснер и Оксенфельд 1933 году, магнитное поле всегда нулевое. Если образец сверхпроводника переходит в сверхпроводящее состояние, то магнитное поле внутри него сразу же становится равным нулю, независимо от того, находился ли образец до перехода во внешнем магнитном поле или нет.

Магнитное поле вытесняется из сверхпроводника наружу. Отсюда делается вывод, что сверхпроводник и идеальный проводник по своей природе принципиально различаются.

ОБЗОР ТЕОРИЙ СВЕРХПРОВОДИМОСТИ

Первой попыткой объяснения сверхпроводимости стала теория братьев Г. Лондон и Ф. Лондон (1935). Были полученные уравнения, описывающие многие свойства сверхпроводников. Предполагалось, что электроны в сверхпроводнике можно рассматривать в виде двух коллективов: сверхпроводящих и нормальных электронов (двухжидкостная модель).

При нуле градусов все электроны превращаются в сверхпроводящие. При увеличении температуры плотность сверхпроводящих электронов уменьшается и обращается в ноль при Т=Т_к . Сверхпроводящие электроны не испытывают сопротивления при движении. Электрического поля для такого движения не нужно - сверхпроводящие электроны движутся как бы по инерции. В отсутствие электрического поля нормальные электроны покоятся.

Сверхпроводник не оказывает никакого сопротивления только в случае, когда ток постоянный. В случае переменного тока сопротивление отлично от нуля и тем больше, чем выше частота переменного тока.

Магнитное поле не равно нулю в тонком поверхностном поле, толщина которого дается выражением

Гинзбург и Ландау применили феноменологический подход к теории сверхпроводимости, учитывающий квантованность явления и описали его как фазовый переход второго рода. Фазовым переходом второго рода называется переход без изменения агрегатного состояния. Меняется только симметрия кристаллической решетки и ход температурной зависимости физических величин.

Позже (1961) Дивером и Фейрбэнком было экспериментально обнаружено квантование магнитного потока, связанного со сверхпроводящим кольцом. Поместим кольцо в магнитное поле при T > T_c . Понизим температуру и переведем кольцо в сверхпроводящее состояние, после этого выключим магнитное поле. По закону Фарадея-Ленца возникнет индукционный ток, который будет препятствовать изменению магнитного потока. Поскольку сопротивление кольца равно нулю, то этот ток не будет затухать. При этом величина такого «замороженного магнитного потока не может быть произвольной. А выражается формулой

, где n – целое число.

В нормальном проводнике прохождение тока сопровождается выделением тепла (закон Джоуля-Ленца). Это тепло возникает из-за соударений электронов с кристаллической решеткой. Кинетическая энергия электронов превращается в энергию колебаний решетки (тепловую энергию).

Тогда суть явления сверхпроводимости можно сформулировать следующим образом: при низких температурах кристаллическая решетка по каким-то причинам не может получать энергию от движущихся электронов. Почему? Чтобы понять явление сверхпроводимости надо вспомнить, что электроны и атомы в кристаллах подчинятся законам квантовой механики, согласно которой энергия может передаваться только определенными порциями - квантами. Квантованы как энергии свободных электронов в кристалле, так и колебания кристаллической решетки. Квантовый характер колебаний решетки проявляется при приближении к абсолютному нулю температур. Решетка может передать электрону только вполне определенную энергию - энергию кванта колебаний. Тогда сверхпроводимость могла бы возникнуть, если бы квант колебательной энергии был бы меньше, чем расстояние между уровнями энергии электронов. В этом случае одного кванта колебаний было бы недостаточно, для того чтобы перевести электрон на другой энергетический уровень. Однако это не так - электроны в металлах являются почти свободными и расстояние между уровнями пренебрежимо мало. Поэтому даже при очень низких температурах отдельные электроны беспрепятственно обмениваются энергией с решеткой.

Теоретически проблему сверхпроводимости в чистых металлах решили Бардин, Купер и Шриффер создав теорию, которая так и называется - теория БКШ. Они предположили, что электроны за счет взаимодействий с колебаниями кристаллической решетки образуют пары, названные куперовскими. Сверхпроводящий ток - это направленное движение пар электронов, возникающее под действием электрического поля. Однако с колебаниями решетки электроны взаимодействуют по отдельности. Поэтому для того чтобы передать энергию паре, колебания решетки должны в первую очередь разрушить пару, а затем уже передать энергию одному из электронов.

Куперовские пары имеют внутреннюю симметрию, для понимания которой надо вспомнить некоторые принципы квантовой механики. Электроны подчиняются принципу Паули, т.е. в одном квантовом состоянии могут находиться не более одного электрона. Вследствие принципа Паули все электроны в твердом теле не могут иметь равные нулю импульсы. Импульсы электронов проводимости последовательно заполняют объем в пространстве импульсов, ограниченный поверхностью, которую называют Ферми поверхность. В теории твердого тела принято вместо импульса p использовать волновой вектор k, связанный с импульсом соотношением:

Р = nk

Электроны обладают еще одной, чисто квантовой степенью свободы спином. Для наглядной интерпретации спин представляют, как вращение электрона вокруг своей оси. Подобно тому, как для произвольно выбранной оси вращения существуют два направления вращения, существуют два направления спина вверх и вниз. Поэтому в каждой точке импульсного пространства могут находиться два электрона со спинами вверх и вниз. Очевидно, что вследствие принципа Паули электроны, находящиеся глубоко внутри Ферми поверхности не могут изменить свой импульс на небольшую величину, т.к. все ближайшие уровни заняты. В проводимости участвуют только электроны находящиеся вблизи Ферми поверхности. При наложении поля электроны вблизи поверхности Ферми меняют свой импульс. Принцип Паули не препятствует этому, т.к. соседние состояния свободны. Так возникает обычный ток в проводниках.

Теперь надо понять, как может возникнуть сверхпроводящий ток. Из квантовой механики известно, что при взаимодействии двух электронов возникают два энергетических уровня: один с энергией большей, чем сумма энергий двух состояний, а другой с меньшей энергией. И пара электронов занимает самый низкий энергетический уровень. Теперь уже, прежде чем передать импульс электрону, колебания решетки должны разрушить пару, а для этого энергия кванта колебаний решетки должна быть больше энергии связи пары. Таким образом, БКШ оставалось найти тип взаимодействия между электронами и определить структуру пары. Согласно теории БКШ в пару связываются два электрона с противоположными импульсами лежащими на поверхности Ферми. Полный импульс пары равен нулю. При наложении электрического поля импульсы электронов в паре немного меняются, и центр масс пары начинает двигаться в направлении, противоположном направлению вектора напряженности. Электроны в куперовской паре в обычных сверхпроводниках паре имеют противоположные спины. Такая пара называется синглетной. Энергия пары понижается за счет взаимодействия с фононами (колебаниями решетки). Последнее предположение подтверждается изотопическим эффектом. Атомы заменяли на изотопы - атомы с таким же числом протонов, но с другой атомной массой при этом менялась температура перехода. Поскольку энергия колебаний решетки зависит от массы атомов, то из наличия изотопического эффекта делают вывод о природе потенциала притяжения между электронами. Важным свойством классических БКШ сверхпроводников является также изотропность (сферическая симметричность) куперовского спаривания. Все электроны с определенной величиной импульса вне зависимости от его направления одновременно при понижении температуры образуют куперовские пары.

Сформулируем теперь основные свойства сверхпроводников, которые следуют из теории БКШ:

1. Куперовские пары синглетные (спины электронов в паре направлены противоположно).

2. Сверхпроводящее состояние сферически симметрично

3. Магнитные поля препятствуют сверхпроводимости.

4. Сверхпроводимость обусловлена электрон-фононным взаимодействием.

5. Сверхпроводимость наблюдается в чистых металлах.

ВИХРИ АБРИКОСОВА

Для объяснения механизма проникновения магнитного поля в поверхность сверхпроводника второго рода [1] оказалось весьма плодотворным представление об электронных вихрях, разработанное А. А. Абрикосовым и подтвержденное экспериментально. В самом простом случае вихрь представляет собой тонкую цилиндрическую трубку (с радиусом порядка 0,1 мкм), через которую магнитный поток может проникать внутрь сверхпроводника (Рис 2). Магнитное поля поддерживается в вихре электрическими токами, которые текут вокруг оси трубки.

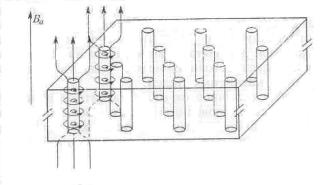
Рис 2. Схема смешанного состояния (шубниковская фаза). Магнитное поле и сверхпроводящие круговые токи показаны на двух нитях вихрей [1].

Вихрь, по сути, является отверстием в сверхпроводнике и магнитный поток, проходящий через него должен квантоваться. Согласно решению Абрикосова вихри образуют регулярную решетку, структура которой в случае смешанного состояния была установлена в экспериментах по упругому рассеянию нейтронов.

ПРОБЛЕМЫ ВЫСОКОТЕМПЕРАТУРНОЙ СВЕРХПРОВОДИМОСТИ

В 1986 г. появилась работа Мюллера и Беднорца, в которой сверхпроводимость была обнаружена в оксидах La_1,8Ba_0,2CuO₄ при необычно высоких температурах T_c=100 K. Этот новый тип сверхпроводимости был назван высокотемпературным ВТСП. Примечательно, что работа, за которую впоследствии дали Нобелевскую премию, была опубликована не в самом престижном физическом журнале Физикал Ревью, издающемся в США, а в немецком журнале Цайтшрифт Фюр Фюзик. Дело в том, что авторы первоначально послали статью в Физикал Ревью, но рецензенты отклонили статью: потому что сверхпроводимости в оксидах, да еще при такой высокой температуре не может быть! Аналогичная история произошла с этими же соединениями и в СССР. Эти соединения были синтезированы И. С. Шаплыгиным и В. Б. Лазаревым в Академии Наук СССР в 1979 г. Авторы обнаружили необычную температурную зависимость проводимости в этих соединениях. Проверять же на сверхпроводимость при более низких температурах не стали, потому что не могли предположить, что их образцы сверхпроводящие. Они это проверили только после Мюллера и Беднорца!

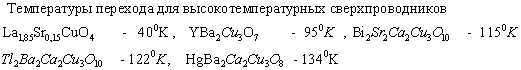
Но еще за 2-3 года до открытия ВТСП были получены сверхпроводники не с такой рекордной T_c, но столь же необычные по свойствам – так называемые сверхпроводники с тяжелыми фермионами ТФСП. Это UPt₃, (T_c=0,55 K) UBe₁₃ (T_c=0,8 K) Sr₂RuO₄ (T_c=1,5K), UPd₂Al₃ (T_c=2K), PrOs₄Sb₁₂ (T_c=1,85 K). ВТСП и ТФСП объединяются одним словом - необычные сверхпроводники. Согласно принятому сейчас определению, необычными называются сверхпроводники, у которых сверхпроводящее состояние не является сферически симметричным, т.е. куперовского спаривания нет в некоторых точках и на линиях поверхности Ферми. Необычные сверхпроводники экспериментально отличаются от обычных по температурной зависимости физических величин. В обычных сверхпроводниках температурная зависимость физических величин, таких как теплопроводность, экспоненциальная. В необычных сверхпроводниках температурная зависимость физических величин степенная.

Еще одним важным свойством сверхпроводящего состояния является его четность, т.е. как изменяется волновая функция пары под действием пространственной инверсии I. В школьной геометрии рассматривают фигуры центрально симметричные, которые не меняются при замене знака всех координат и фигуры, не обладающие таким свойством. В квантовой механике, если структура кристалла центрально симметричная, то возможны два состояния, характеризующиеся действием инверсии I на волновую функцию Ψ(R). Четное состояние:

Нечетное состояние:

Согласно законом квантовой механики если спины электронов в паре направлены противоположно (синглетная пара), то волновая функция четная, а если одинаково (триплетная пара), то волновая функция нечетная. Экспериментальные исследование новых типов сверхпроводников обнаружили, что во многих из них сверхпроводящее состояние имеет нечетную волновую функцию и спины электронов в паре параллельны. Это позволило сделать вывод еще об одном их необычном свойстве: сверхпроводимость в некоторых из них( UBe₁₃ UPt₃ Sr₂RuO₄, UPd₂Al₃ PrOs₄Sb₁₂) имеет триплетный характер, но некоторых, например в ВТСП –синглетная.

Межэлектронные взаимодействия всегда приводят к тому, что из-за взаимодействия двух одноэлектронных состояний возникают два возможных многоэлектронных, одно с меньшей энергией (основное), а другое с большей энергией (возбужденное) и оба электрона занимают основное состояние. Тип взаимодействия определяет, какое из состояний будет основным – синглетное или триплетное. Несмотря на то, что за прошедшие боле 20 лет создано много теорий, а число публикаций исчисляется тысячами, типы взаимодействий, приводящих к сверхпроводимости в необычных сверхпроводниках пока достоверно не известны. Известно, только то, что во многих ТФСП взаимодействие электронов в паре связано с магнетизмом. Некоторые атомы в кристаллах имеют собственные магнитные моменты, связанные с тем, что спины атомных электронов ориентированны параллельно. Моменты соседних атомов могут ориентироваться параллельно – такая структура называется ферромагнитной, или антипараллельно – такая структура называется антиферромагнитной. Во многих необычных сверхпроводниках (например UBe₁₃ , UPt₃ ) при понижении температуры до приблизительно 10T_c наблюдается антиферромагнитной переход. Сосуществование антиферромагнитной структуры и сверхпроводимости достоверно наблюдается в UPd₂Al₃, а в Sr₂RuO₄, и PrOs₄Sb₁₂ обнаружены спонтанные магнитные поля. Таким образом, если в БКШ сверхпроводниках магнитное поле разрушает сверхпроводимость, то в необычных сверхпроводниках внутренние магнитные поля каким-то образом поддерживают сверхпроводимость.

ЗАКЛЮЧЕНИЕ

Сформулируем теперь 5 основных особенностей необычных сверхпроводников:

1. Куперовские пары могут быть как синглетными так и триплетными.

2. Сверхпроводящее состояние не является сферически симметричным. На Ферми поверхности существуют линии, и точки где отсутствует куперовское спаривание.

3. Сверхпроводимость каким-то образом связана с магнитной структурой кристалла.

4. Конкретные взаимодействия приводящие к сверхпроводимости неизвестны, понятно только что природа этих взаимодействий может различаться.

5. Сверхпроводимость наблюдается в интерметаллических соединениях и в ионных кристаллах.

Мы видим, что эти пять особенностей необычных сверхпроводников коренным образом отличаются от особенностей обычных сверхпроводников. Существующая теория (теория БКШ), правильно описывает частный случай, но не является всеобщей. Последующие исследования опровергли многие из ее общих выводов, но не опровергли ее логику. Это вселяет надежду, что проблема высокотемпературной сверхпроводимости будет решена и будут созданы сверхпроводники, работающие при комнатной температуре.

Другим перспективным направлением исследований механизма высокотемпературной сверхпроводимости является изучение механизма сальтаторной проводимости нейронов, имеющих спиральные миелиновые оболочки [2]. По-видимому, для них может быть применен формализм модели квантовых вихрей Абрикосова.

ЛИТЕРАТУРА

1. Ципенюк Ю. М. Физические основы сверхпроводимости. - М.:1996.

2. Холманский А. С. Моделирование физики мозга //Математическая морфология. Электронный математический и медико-биологический журнал. – Т. 5. – Вып. 4. - 2006. - URL: www.smolensk.ru/user/sgma/MMORPH/N-12-html/holmansky-4/holmansky-4.htm

The Problems of hightemperature overconduction

Lobachev V.V., Yargemskiy V. G., Kholmanskiy A. S.

Review of some problems of hightemperature overconduction carry out.

*Московский государственный университет инженерной экологии (МГУИЭ).

**Московский государственный медико-стоматологический университет (МГМСУ)

Поступила в редакцию 29.11.2007.