-
Математическая морфология.
Электронный
математический и медико-биологический журнал. - Т. 6. -
Вып. 4. -
2007. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/TITL-16.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/cont.htm
УДК 004.252
Анализ
производительности обработки упакованных поисковых деревьев в модели
иерархической памяти
Ó
2007 г. Смирнов В. В.
Для
иерархической памяти анализируется производительность операций упорядоченного и
случайного поиска: в упакованном в массив k-арном
сбалансированном дереве; в двоичном сбалансированном поисковом дереве на основе
связанных списков из библиотеки STL (rbtree); в гибридном
поисковом дереве на основе btree.
Ключевые
слова: модель иерархической памяти, поисковые
деревья.
Введение
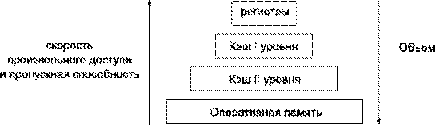
Память
современных вычислительных систем имеет явно выраженную иерархическую
структуру, включающую несколько уровней, параметры которых влияют на
производительность вычислений. Чаще всего встречается четырехуровневая
иерархическая модель памяти, включающая регистры процессора, кэш-память первого
(L1) уровня, кэш-память второго (L2) уровня и оперативную память (RAM), пример
которой дан на рисунке 1. В ряде случаев в иерархии можно встретить так же
кэш-память третьего уровня и внешнюю память на жестких дисках.
|
|
Рисунок 1
– Пример иерархической организации памяти вычислительной системы
Для
иерархической модели памяти характерны фундаментальные соотношения между
объемом памяти некоторого уровня и скоростью произвольного доступа к нему: чем
больше объем, тем ниже скорость произвольного доступа. Ассоциативная кэш-память
промежуточных уровней иерархии позволяет существенно повысить быстродействие в
задачах, для которых наблюдается свойство временной локальности обращений к
памяти: в любой произвольно выбранный промежуток времени алгоритм обращается к
небольшому подмножеству основного рабочего множества. Поскольку скоростные
характеристики памяти обычно меняются на порядок при переходе от уровня к
уровню, также может меняться и производительность, если соблюдается свойство
временной локальности. В противном случае кэш-память не вносит существенного
влияния в производительность всей подсистемы памяти [1].
Не
все алгоритмы демонстрируют свойство временной локальности в явном виде: в
самом алгоритме или в модели данных. В этом случае требуется их переработка
вплоть до полного перепроектирования с учетом особенностей иерархии памяти
конкретного процессора. При этом алгоритм становится «привязанным» к данной
архитектуре, так как при переходе на другую архитектуру с другими
характеристиками (в основном, объемом кэш-памяти) может наблюдаться
значительное падение производительности.
В
современных программах широко применяются динамические структуры данных, такие
как связанные списки (list) и построенные на их основе деревья (tree),
множества (set) и отображения (map). Все они одинаково важны, так как в
совокупности перекрывают большинство известных алгоритмов обработки данных.
Связанные списки понятны и просты в реализации, но их базовая структура данных
на основе указателей плохо соотносится с иерархической моделью памяти. Обычно
используется базовый метод выделения динамической памяти под узлы списка,
который не учитывает шаблон доступа к данным и не знает ничего о структуре
кэш-памяти. Как результат, активная работа со списком (удаление и вставка
узлов) приводит к хаотическому их распределению по объему памяти и к нарушению
свойства временной локальности. В этом случае даже последовательный
упорядоченный перебор узлов дерева будет приводить к обращению по случайным адресам
памяти.
В
настоящей работе рассматривается способ организации узлов сбалансированного
поискового дерева, учитывающий особенности организации кэш-памяти современных
процессоров, и проводится анализ производительности серии операций
упорядоченного и произвольного доступа.
Особенности организации кэш-памяти
Основными
характеристиками кэш-памяти являются: объем, время произвольного доступа
(латентность) и размер блока данных, считываемого за одну операцию. Типичные
характеристики уровней иерархической памяти современных вычислительных систем
представлены в таблице 1 [2, 3].
Таблица 1
–Типичные временные и пространственные характеристики уровней иерархии памяти
|
Уровень памяти |
Время произвольного
доступа, такты |
Размер, Kb |
Размер блока, байт |
|
Регистры |
1 |
32–1024 байт |
1–4 |
|
L1 |
3–4 |
16–64 |
32-64 |
|
L2 |
12–28 |
256–4096 |
32-64 |
|
RAM |
250–500 |
>> 1024 |
16 |
Из
таблицы 1 видно, что основные показатели отличаются примерно на порядок при
переходе от одного уровня организации к другому. Так, доступ к данным в
регистрах процессора осуществляется максимально быстро, но их количество сильно
ограничено. Доступ к данным в L1 потребует 3–4 такта, однако за это время могло
быть выполнено несколько (на суперскалярных процессорах с высоким IPC – до
десяти, иногда и более) команд над данными в регистрах. И, наконец,
произвольный доступ к одной ячейке RAM может «стоить» нескольких сотен команд
над регистрами.
Особняком
в иерархической модели памяти стоит механизм (аппаратной и программной)
предвыборки данных, не показанный на рисунке 1. Он состоит в том, что процессор
может затребовать в L1, L2 или RAM данные заранее до того, как они реально
начнут обрабатываться. Тем самым маскируется латентность доступа к данным,
поскольку к моменту обработки уже пройдет часть периода латентности. Важной
особенностью механизма предвыборки является то, что он работает только в
пределах страницы виртуальной памяти, размер которой обычно составляет 4Кбайт.
В
настоящей работе предлагается вариант способа улучшения временной локальности
за счет пространственной локальности организации данных в памяти. Данные меду
уровнями иерархии передаются блоками по 32–64 байта, время передачи блока
вносит некоторый (иногда значительный) вклад в латентность доступа. Чем чаще
запросы попадают в границы одного и того же блока, тем меньше (в среднем)
латентность.
Имеется
еще один фактор, влияющий на производительность вычислений – формат хранения
данных в RAM. Чем меньше размер рабочего множества данных в абсолютном
выражении, тем выше эффективность кэширования. Упакованный, сжатый формат
хранения может дать выигрыш в быстродействии, если время на распаковку меньше
среднего времени доступа к данным. Особенно это актуально для RAM, латентность
которой составляет сотни тактов. За это время процессор может выполнить
значительный объем работы по преобразованию данных из формата хранения в формат
обработки и обратно.
Множество на основе упакованного
сбалансированного m-арного дерева
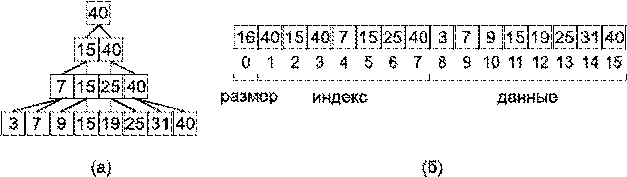
Добиться
пространственной локальности можно за счет того факта, что деревья можно
упаковать в одномерный массив [4]. В частности, легко поддаются упаковке
сбалансированные m-арные деревья, используемые для представления множеств.
Пример такой упаковки показан на рисунке 2.
|
|
Рисунок 2 –
Пример упаковки двоичного сбалансированного поискового дерева в одномерный
массив: (а) структура дерева, (б) упаковка дерева в массив
Упаковка
дерева в массив дает два положительных эффекта. Первый из них состоит в том,
что узлы дерева одного уровня расположены в смежных ячейках массива, поэтому
поиск может выполняться, в основном, в пределах одного блока памяти, что
существенно повышает вероятность успешной предвыборки и снижает латентность
доступа к данным. Второй эффект состоит в отсутствии явных указателей, роль
которых теперь выполняют неявные соотношения между индексами ячеек. В
результате отсутствия явных указателей на узлы, упакованное поисковое дерево
более компактно по сравнению со своим аналогом на основе связанных списков.
Компактность структуры данных уменьшает относительный размер рабочего множества
и повышает эффективность кэширования.
Для
исследования влияния эффекта пространственной локальности на временную
локальность разработана структура типа множество (tree-set), на основе
упакованного сбалансированного поискового дерева. Арность дерева выбирается,
исходя из размера строки кэш-памяти и кратна ей. Проведен ряд экспериментов по
оценке производительности серии операций произвольного и случайного доступа
типа проверки факта вхождения элемента в множество. Каждая из таких операций
выполняется посредством навигации по уровням упакованного поискового дерева в
направлении от корня к листьям по одной из ветвей. Для выбора следующего узла
необходимо выполнить O(k)
операций сравнения, где k – арность поискового дерева, константа,
выбираемая исходя из структуры кэш-памяти.
Серия
экспериментов включает оценку времени выполнения 4M операций поиска элементов,
каждый из которых заведомо присутствует в дереве, иными словами, каждый поиск
проходит путь длины logkN
от корня к листу, где N – количество элементов в множестве, k
– арность дерева. Варьируемыми параметрами являются:
·
арность поискового дерева, значение которой
выбирается в пределах 4–512 и является степенью 2;
·
количество элементов в множестве в пределах 1K –
128M, является степенью 2;
·
тип доступа:
·
упорядоченный (sequential read), проверка факта
присутствия элементов в множестве в порядке возрастания их абсолютного
значения;
·
случайный (random read), на каждой итерации генерируется
случайный ключ в пределах 1–N (все
эти элементы присутствуют в множестве);
·
связка процессор-память:
·
Intel Сore 2 Duo Merom T7200, 32K L1 кэш, 4M L2
кэш, 1Gb RAM DDR2 PC5300, одноканальная (далее Core 2 Duo, C2D);
·
Intel Pentium 4 Nortwood, 16K L1 кэш, 512K L2
кэш, 1Gb PAM DDR PC2700, одноканальная (далее Pentium 4, P4).
Проводится
тестирование структуры данных типа множество на основе двоично
сбалансированного дерева из библиотеки C++ STL (на основе связанных списков).
Ниже
также приведены сравнительные данные, полученные в аналогичных условиях для
динамического поискового дерева типа btree на основе упакованных
сбалансированных деревьев.
Тестирование упакованного поискового
дерева
Влияние арности поискового дерева
На
рисунке 3 представлен сводный график зависимости производительности
случайного поиска от арности поискового дерева, значение которой изменялось в
пределах 4–512.
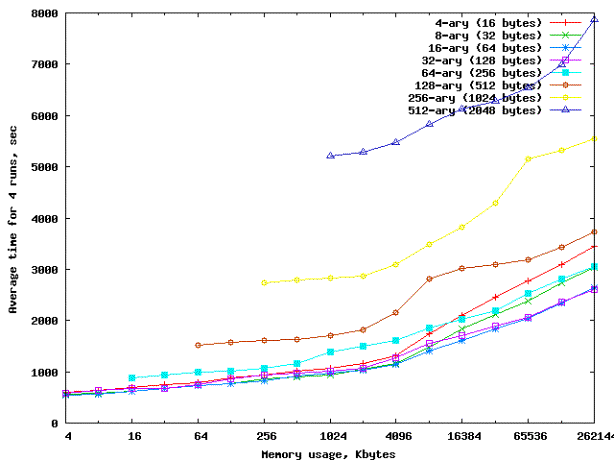
Рисунок 3
– Зависимость производительности упорядоченной и случайной выборок от арности
поискового дерева для процессора Core 2 Duo
На
сводном графике видно, что производительность поисковых операций растет с
ростом арности до значения 16–32, а затем сильно деградирует. Таким образом,
тест показывает, что оптимальным размером блока данных для потомков узла
является 64–128 байт, что составляет 2–4 строки кэша по 32 байта. Так же виден
характерный скачек времени выполнения в районе 4M размера поискового дерева.
Это соответствует размеру кэша L2 для системы C2D. На рисунке 4 эти данные
представлены в наглядном трехмерном формате.
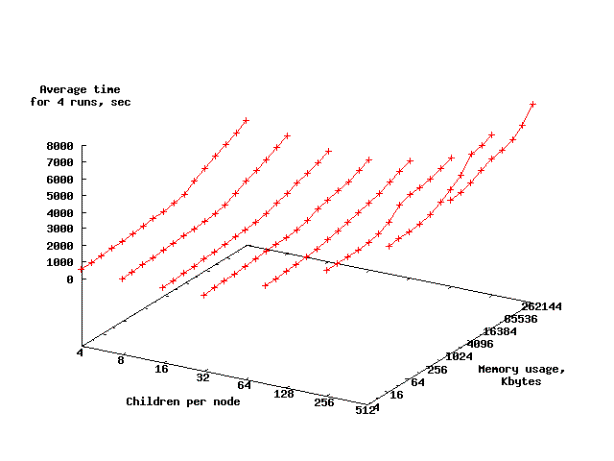
Рисунок
4 – Зависимость производительности упорядоченной и случайной выборок
от арности поискового дерева для процессора Core 2 Duo
Также
следует отметить, что производительность поисковых операций для оптимальной
арности дерева незначительно (десятки процентов) деградирует с переходом через
отметки 32K (когда данные умещаются в кэше L1 и задержки минимальны) и 4M
(когда данные умещаются в кэше L2). На графиках это проявляется в виде
изменения наклона соответствующих зависимостей. Прямая линия роста времени
выполнения теста означает основной вклад глубины поискового дерева, которое
линейно растет с ростом его размера. Таким образом, латентность памяти
эффективно скрывается механизмом предвыборки.
Кривизна
линии производительности означает влияние посторонних факторов, которые
подробно рассматриваться не будут. Основным из них можно отметить влияние
буфера трансляции виртуальных адресов TLB, промах в котором означает
максимально высокую латентность соответствующего запроса к данным.
Влияние типа процессора, размера L1, L2 и
типа RAM на производительность операций упорядоченной и случайной выборок
На
рисунке 5 представлен сводный график зависимости производительности операций
упорядоченной и случайной выборок на двух различных архитектурах процессора: P4
и C2D.
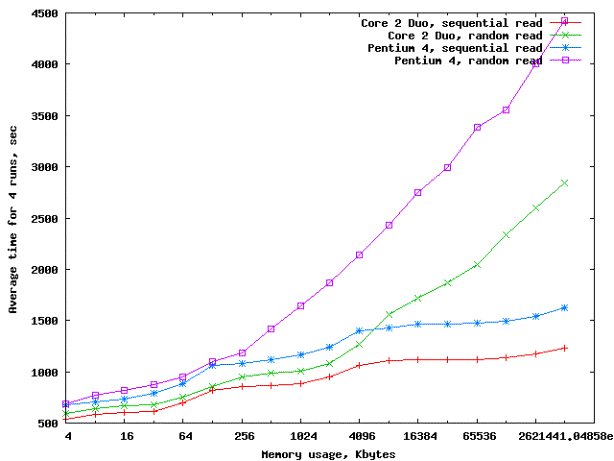
Рисунок 5
– Сводный график зависимости времени выполнения поисковых операций от
архитектуры процессора и типа памяти
На
графике видны практически плоские с очень незначительным наклоном линии времени
выполнения тестов в соответствующих частях горизонтальной оси для случая
упорядоченной выборки. Это означает, что производительность поисковых операций
определяется совокупной пропускной способностью иерархии памяти для данного
типа алгоритма, а соответствующие латентности эффективно скрываются механизмами
предвыборки данных.
Для
случая произвольного доступа можно сделать вывод, что его показатели
соответствуют случаю упорядоченного доступа, когда рабочее множество умещается
в соответствующий кэш, однако, в противном случае наклон линии резко меняется.
Это объясняется возросшим влиянием латентности, которая теперь не может быть
также эффективно маскирована предвыборкой, как в случае упорядоченного доступа.
Сравнение производительности поисковых
операций в упакованном дереве и в дереве на основе связанных списков
На
рисунке 6 представлен сводный график зависимости времени выполнения поискового
теста для упакованного дерева и дерева на основе связанного списка типа rbtree
[5] из библиотеки C++ STL на машине C2D.
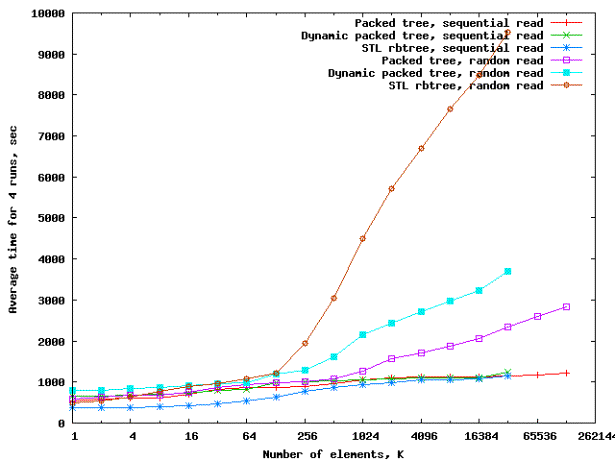
Рисунок
6 – Сводный график времени выполнения поисковых тестов для случаев
упорядоченного и произвольного доступа в упакованном дереве арности 32 и
бинарном дереве на основе связанных списков из библиотеки STL, архитектура Core
2 Duo
Для
случаев упорядоченной выборки обе структуры имеют практически одинаковые
зависимости, дерево на основе связанных списков имеет заметно лучшую (до 100%)
производительность при попадании рабочего множества в кэш соответствующего
уровня. В случае же попадания в область RAM обе структуры данных демонстрируют
одинаковую производительность. Таким образом, при последовательном доступе производительность
зависит, в основном, от совокупной пропускной способности иерархической памяти
и почти не зависит от алгоритма.
Следует
отметить, что совокупная пропускная способность памяти меньше теоретической для
данного типа RAM и, в общем случае, зависит от алгоритма. Однако данный тест не
выявил такой зависимости.
В
случае же произвольного доступа, производительность дерева на основе связанного
списка сильно деградирует, и для случая 32M элементов разница достигает 4 раз.
Таким
образом, несмотря на то, что при
навигации по упакованному дереву с высокой (32) арностью необходимо выполнить
значительно больший фактический объем вычислений, чем для дерева арности 2 из
библиотеки STL, общая производительность оказывается значительно выше, так как
время ожидания данных оказывается существенно меньше.
Для
оценки абсолютных и относительных величин производительности разработана
динамическая структура данных, являющаяся гибридом упакованного поискового
дерева и динамического дерева типа btree [5], обычно используемого при работе с
внешней памятью. Гибридизация в данном случае состоит в том, что в каждом узле
дерева btree (размер которого в данном случае выбран 4096 байт или 1024
элемента) организуется упакованное поисковое дерево вместо линейного массива,
как в базовой реализации btree.
На
сводном графике (рисунок 6) данные для гибридного динамического дерева
отмечены как «Dynamic packed
tree». Из графика видно, что для случая упорядоченного доступа
время выполнения теста почти точно соответствует временам для STLrbtree и
простого упакованного дерева (packed
tree). В случае же случайного доступа показатели гибридного
динамического дерева лишь немногим (менее чем в 2 раза) хуже соответствующих
показателей для статического упакованного дерева и значительно лучше показателей
для бинарного дерева на основе связанных списков (STL rbtree).
Тест многопоточности: влияние совокупной
пропускной способности памяти
На
рисунке 7 представлены результаты тестирования упакованного поискового дерева в
многопоточном и однопоточном режимах. Многопоточность обеспечивается за счет
одновременного запуска двух процессов.
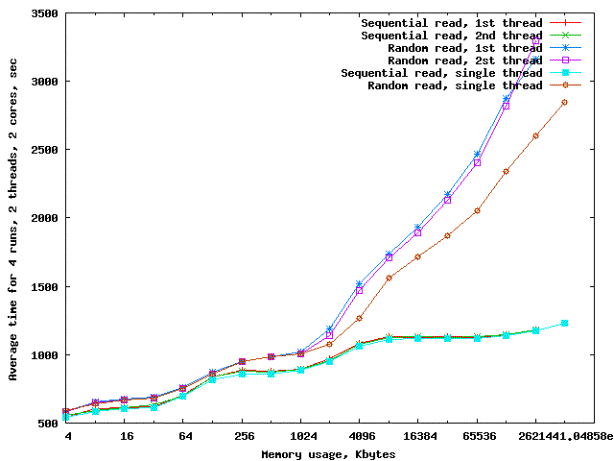
Рисунок 7 – Результаты
тестирования производительности упорядоченного и случайного поиска в
многопоточном и однопоточном режимах, Core 2 Duo, арность упакованного дерева –
32
Из
графика видно, что в случае упорядоченного доступа производительность
практически одинаковая (коэффициент масштабирования равен 1) для однопоточного
и многопоточного тестов, независимо от того, в какую из областей попадает
размер рабочего множества. Это означает, что для исследуемых типов структуры
данных и выборки не достигается максимальная пропускная способность памяти и,
более того, параллельно работающие ядра C2D не конфликтуют при доступе к
памяти.
Для
случайного типа доступа наблюдается расхождение в величинах времени выполнения
теста для однопоточного и многопоточного случаев. Как видно из графика,
коэффициент масштабирования поискового алгоритма составляет приблизительно 0.8.
На
рисунке 8 представлены результаты тестирования бинарного сбалансированного
поискового дерева из библиотеки STL (Rbtree).
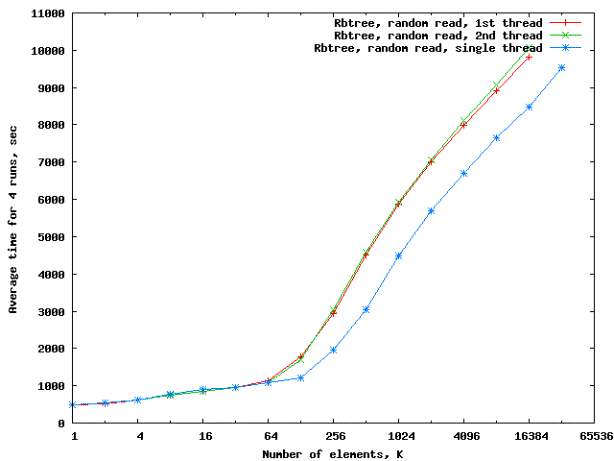
Рисунок 8
– Сводный график результатов тестирования производительности случайного доступа
для бинарного дерева на основе связанных списков (STL Rbtree) в однопоточном и
двухпоточном режимах, Core 2 Duo
Результаты
на графике 8 показывают примерно такой же коэффициент масштабирования, как и
для случая упакованного дерева (рисунок 8): 1 в случае попадания в область кэша
и 0.8 -- в случае попадания размера рабочего множества в область RAM.
Заключение
Таким
образом, как упорядоченный, так и случайный методы поиска в упакованном дереве
показывают неплохие относительные величины производительности и многопоточной
масштабируемости. Результаты тестов говорят о том, что можно значительно улучшить
временную локальность в случае произвольного доступа, если организовать данные
в соответствии с особенностями кэш-памяти. Эффективное использование кэша
приводит к тому, что, несмотря на значительно больший объем вычислений в случае
упакованного дерева высокой арности, производительность относительно дерева на
основе связанных списков оказывается значительно выше.
Поисковые
структуры данных на основе связанных списков разрабатывались в то время, когда
время выполнения машинной инструкции было сопоставимо со временем произвольного
доступа в память, и процессор являлся «узким местом» вычислительной системы.
Упакованные деревья дают гораздо лучшие результаты производительности на
архитектурах с многоуровневой организацией памяти, которые к настоящему времени
применяются практически повсеместно. Кроме этого, они значительно более
компактны, так как не содержат в явном виде указателей, на которые расходуется
значительный объем памяти.
Следует
также отметить, что производительность произвольного доступа относительно слабо
деградирует при переходе размера рабочего множества через величину кэша L2.
Таким образом, можно предположить, что упакованное дерево будет показывать
неплохие абсолютные и относительные результаты на процессорах без большого L2,
применяемых во встраиваемых системах и мобильных телефонах.
И,
наконец, указанные принципы организации данных можно распространить и на
внешнюю память на жестких дисках, имеющую высокую (миллисекунды) латентность
произвольного доступа, которая растет по мере физического «удаления» блоков
данных друг от друга.
Список литературы
1. Корнеев
В., Киселев А. Современные микропроцессоры. – СПб: БХВ-Петербург, 2003.
2. Intel Core 2 Duo
Processor [Электронный ресурс]: Электр. дан. и текст. дан. Intel Corporation. Режим доступа
http://www.intel.com/design/core2duo/documentation.htm
3. Intel Pentium 4 Processor Family [Электронный ресурс]:
Электр. дан. и текст. дан. Intel
Corporation. Режим
доступа
http://www.intel.com/design/Pentium4/documentation.htm
4. Benoit, D., Demaine, E. D., Munro, J. I.,
Raman, R., Raman, V., and Rao, S. S. Representing Trees of Higher Degree. Algorithmica
43, 4 (Dec. 2005), pp. 275–292.
5. Ахо
А., Хопкрофт Д., Ульман Д. Структуры данных и алгоритмы.: – М: Издательский
дом «Вильямс», 2001.
Performance Analysis of Packed Search Trees in the
Hierarchical Memory Model
Ó 2007 г. Smirnov V. V.
Performance of ordered and random search operations is
analyzed using k-ary tree packed in an array, binary balanced search tree based
on linked lists from STL library (rbtree). Dynamic version of packed k-ary tree
have been developed and it's performance have been estimated.
Key words: hierarchical memory model, search trees.
Кафедра вычислительной техники
Филиал ГОУ ВПО «МЭИ (ТУ)» в г. Смоленске
Поступила
в редакцию 26.12.2007.