- Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 6. -

Вып. 4. - 2007. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/TITL-16.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/cont.htm

УДК 515.16:577.3

ОБРАЗОВАНИЕ ПОРЫ В БИОЛОГИЧЕСКОЙ МЕМБРАНЕ СКВОЗЬ ОДНОСТОРОННЮЮ ПОВЕРХНОСТЬ

(tukembaev-1.doc)

Ó 2007 г. Тукембаев Ч. А.

Для образования поры в мембране предлагается новая односторонняя поверхность. Новая односторонняя поверхность в виде тела вращения не содержит явных самопересечений в трехмерном пространстве. Представляет собой диафрагму, т.е. является физическим объектом, как лист Мебиуса и бутылка Клейна. Переход в 4-мерное пространство заменен кручением так, что односторонняя поверхность имеет точки перегиба только в центе симметрии, где кручение меняет знак. Новый объект, как диафрагма внутри поры, объясняет образование поры и ионного канала в биологической мембране, оптическую активность и чувствительность клеток к слабым электромагнитным полям, и эффект Ханле. Решение проблемы оптической активности вещества основано на знаке кручения, т.е. определяется правой или левой парой бинормалей.

Библиография: 12 назв. Рисунок. Построение односторонней поверхности.

Оптическая активность, взаимодействие клеточных культур на расстоянии, образование поры и ионного канала в биологической мембране являются важными проблемами биофизики [1-8]. Клетка со сферической или цилиндрической поверхностью приобретает форму тургора – клеточной “тени” в момент образования поры [8]. Проблема содержит особенность, непреодолимую известными методами решения, так как пора образуется вблизи критической температуры фазового перехода из жидкого кристалла в гель при наличии флуктуаций тока [6-7]. Диффузия Бронштейна-Исеровича (БИ) [5] отличается от диффузии Эйнштейна [7] образованием вихрей и радиусом поры, соответственно в степени 3 или 2. Флуктуации тока в [7] должны подчиняться формуле Найквиста, но зависят от закона Ома, поэтому являются микротоками, но фазовый переход более сложный процесс, чем диффузия. В данных вопросах отводится важная роль электрохимии в биологии [3]. Это касается эффекта Фарадея в проблеме Пастера [1] и чувствительности клеток к слабым электромагнитным полям. Например, в области оптической активности возникает эффект Ханле, взаимодействие полей клеточных культур, разделенных расстоянием [2].

Каким образом клетка сдавливается до формы тургора в отсутствие сил метода Тазавы [8]? Однако напряжения сдвига являются непременным условием формирования ионного канала [9, 10]. С другой стороны, реальными объектами односторонних поверхностей являются лист Мебиуса и бутылка Клейна, где самопересечение устраняется переходом в 4-мерное пространство. Для односторонней поверхности в 3-мерном пространстве нет тела вращения, не удается обойти линию самопересечения [11].

Новая односторонняя поверхность в виде тела вращения без явных самопересечений в 3-мерном пространстве устраняет особенность. Переход в 4-мерное пространство заменен кручением t=k^–2[r¢r²r²¢], где кривизна k=|r¢|, r – радиус-вектор, так, что поверхность имеет точки перегиба только в центре симметрии, в котором кручение меняет знак. Сдвиг реализуется через кручение. В точке перегиба нечетные производные 3 или 5 порядка не равны нулю. Тогда, знак кручения определяется левой или правой парой бинормалей, что вносит определенность в оптическую активность. Новый объект, как диафрагма внутри поры, объясняет образование поры и ионного канала в мембране, оптическую активность и чувствительность клеток к слабым электромагнитным полям, и эффект Ханле.

1. В зависимости от отношения a к b вращению овала Кассини

(x²+z²)²–2b²(x²–z²)=a⁴–b⁴

вокруг оси z, где b – расстояние до фокуса, a – параметр, соответствуют 5 случаев:

1) Для a>2^1/2b получается шарообразная поверхность;

2) Если a<b, то получается кольцеобразная поверхность (тор);

3) Когда b<a<2^1/2b, то получаем двояковогнутую по оси z линзу (дискоцит, тургор). Кассиниана содержит 4 точки перегиба, в которых k<0;

4) Если a=2^1/2b, то получаем цилиндрическую поверхность. В 2 точках перегиба на оси z k=0, где кривизна меняет знак;

5) Для a=b получаем узловую поверхность.

Особенность заключена в узле лемнискаты, содержащем 2 точки перегиба, где k=0. Через узловую поверхность сфера трансформируется в тор. Овал Кассини есть решение некоторого уравнения [12], где постоянная интегрирования равна параметру a. Изменением параметра a кассиниана трансформируется из одиночного овала, когда a>b, в два овала, если a<b, поэтому кассиниана является моделью микротоков в мембране. Первые 4 случая демонстрируют все формы, в которые видоизменяется клетка.

В последнем случае точка переходит с внешней поверхности на внутреннюю поверхность, проходя сквозь узел. Две точки перегиба в узле раздвинуты на малое расстояние 2d по разные стороны от узла. Это расстояние является кратчайшим расстоянием между 2 касательными к ветвям лемнискаты в узле (левая или правая пара прямых линий). В точке перегиба вектор Дарбу d=tt+kb становится неопределенным, так как k=0, где t – вектор касательной, b – бинормали сопутствующего трехгранника. В таких точках, в том числе на цилиндрической поверхности, получаем геодезические линии нулевой длины, соответствующие траекториям светового луча. В частности, электрон излучает, двигаясь по касательной в точке перегиба, где скорость и частота излучения, как физические величины, определяются нечетными производными 3 или 5 порядка для вектора Дарбу.

Дальнейшие построения представлены на рисунке 1.

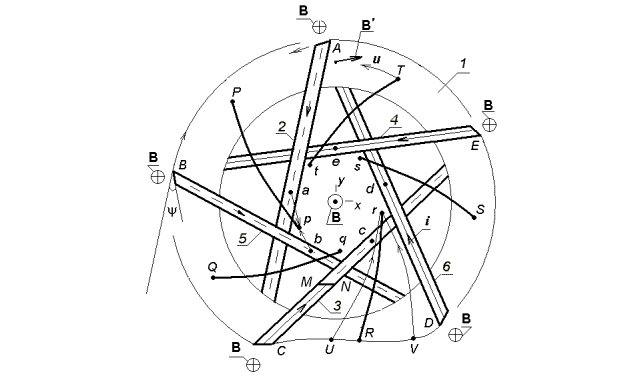
Рис. 1. Построение односторонней поверхности мембраны.

Полоса навивается на тор 1 по восьмерке. На внешней стороне полосы средняя линия отмечена сплошной линией, но на внутренней стороне – штриховой линией. На боковых сторонах полосы имеем бесконечные производные, поэтому направление электрического тока i по меридиану поверхности ограничено каналом и соответствует движению электронов в обратном направлении. Одному полному обходу вокруг внешней окружности тора соответствует 5 отрезков полосы, пересекающих тор вблизи начала координат. Направление вектора магнитной индукции B в начале координат совпадает с осью z (относительно плоскости чертежа вверх) и имеет одинаковую ориентацию с правой системой координат, смешанное произведение которых со знаком плюс. При увеличении числа отрезков расстояние от отрезка до начала координат уменьшается и стремится к d. На линии MN отрезка 3 внешняя и внутренняя стороны полосы склеиваются, поэтому получается односторонняя поверхность, которая соответствует нечетному числу отрезков, но четному числу отрезков – двухсторонняя поверхность. Кручение t выражается углом y (см. рис.), равным p/5, что в сумме составляет p. Направление магнитного момента p_m иона в фокусе определяет кручение, поэтому валентный электрон закручивается в каждом фокусе только и только по правой спирали против направления p_m. Число отрезков равно числу положительных зарядов, движущихся в торе в одном направлении с током I.

Отрезки 6 и 2, как линии, образуют левую пару прямых линий, как и пары отрезков 3 и 2, 4 и 3, 5 и 4, 6 и 5. Получаем левовинтовую навивку полосы на тор. Точки a, b, c, d и e соответственно на серединах отрезков 2, 5, 3, 6 и 4 являются точками перегиба. Теперь, натягиваем боковые стороны отрезков полосы на внешнюю поверхность тора так, чтобы точки перегиба попарно двигались навстречу друг к другу. Например, для половины Bb отрезка 5 и половины Aa отрезка 2 направление растяжения показано стрелками на внешней окружности тора. По ходу движения, левая сторона половины Bb и правая сторона половины Aa притягиваются друг к другу до совмещения в кривую Pp. Точка перегиба b практически сольется с точкой перегиба a, но так, что между точками перегиба b и a получаем узел p. Аналогично поступаем с отрезками 3 и 5, 6 и 3, 4 и 6, 2 и 4, предварительно разбив их на половины, и получаем узлы q, r, s и t, точки Q, R, S и T и кривые Qq, Rr, Ss и Tt, но в целом – диафрагму.

Кольцевидные структуры БИ-модели, периферия которых образована твердым липидом, а в центре расположена жидкая фаза [5, 7], учитываются трансформацией диафрагмы в вихрь. Роль периферии в диафрагме выполняет тор. Внешнюю окружность тора между точками C и D заменим кривой CURVD. Эта кривая имеет точки экстремума U и V и точку перегиба R, в которой кривая пересекается с кривой Rr. Кривая CURVD описывает волну, вращающуюся против часовой стрелки. Как и ранее, притягиваем боковые стороны половин Dd и Cc отрезков 3 и 6 на волнообразную поверхность, образованную кривой CURVD вокруг средней линии тора. Точки перегиба c и d будут двигаться навстречу друг другу и сомкнутся в узле r. Линия Rr состоит из точек перегиба, линии Ur и Vr – из экстремальных точек. В узле r правосторонней и левосторонней производных нет, аналогично тому, как их нет для функции f(x)=xsin(1/x), когда x=0, где ось x совпадает с линией точек перегибов Rr, а x=0 – с узлом r. Соответствует нулевой кривизне, т.е. геодезическим линиям нулевой длины (траекториям светового луча). Точка перегиба R и экстремальные точки U и V сливаются в узел r. Указанные действия переносим на другие половины пар отрезков и получаем портрет вихря. Любые малые возмущения преобразуют узловую одностороннюю поверхность (чор) в тор или двояковогнутую линзу.

Рассмотрим образование магнитного поля в диафрагме. Согласно направлению электрического тока i или движению электронов возникает магнитное поле, которое соответствует случаю 5. Такое поле охватывает внешнюю поверхность тора, как внешнее поле, и локализовано внутри тора, как внутреннее поле. Внешнее магнитное поле согласно направлению тока определяется в точках перегиба a, b, c, d и e. По направлению тока i, слева от точек a, b, c, d или e вектор магнитной индукции B направлен вверх в начале координат в полном соответствии движению u положительных зарядов q и тока I внутри тора в правой системе координат. Именно движение зарядов q формирует границу между твердым липидом и жидкой фазой внутри поры. Справа от каждой из точек перегиба за пределами внешней поверхности тора вектор B с внутренним крестиком направлен вниз, перпендикулярно плоскости чертежа, и соответствует внешнему магнитному полю.

Внутреннее магнитное поле образовано вектором магнитной индукции B¢ внутри тора под точкой A. Это поле противодействует движению u зарядов внутри тора. Возникает торможение зарядов. После полной остановки движения заряды начнут двигаться и ускоряться в торе по часовой стрелке, согласно направлению вектора B¢ и силе Лоренца. Тогда, движение положительных зарядов в торе по часовой стрелке приводит к инверсии вектора B в начале координат. Следовательно, вектор B и ось z направлены в противоположные стороны, имеют противоположную ориентацию в правой системе координат, смешанное произведение которых со знаком минус. Значит, оптическая активность изменит знак, что и требовалось доказать. Перемещение тора вдоль оси z вызывают электромагнитную индукцию, концентрические волны и волну, образованную торможением зарядов.

Клетка излучает только в точках перегиба, т.е. в случаях 3, 4 и 5 имеет место биогенное излучение. Исходя из закона Био ¶B/¶t=m₀miR^–2ds/dt, определим значение R. В центре тора образуется пора радиусом R=(b²–a²)^1/2, если a<b. Магнитное поле локализовано внутри тора. В случае a>b пора закрыта, так как начальные данные таковы, что R=(a²–b²)^1/2. Следовательно, начальные данные определяются микротоками в мембране. В свою очередь, микротоки зависят от квантовых физико-химических свойств мембраны.

В случае b<a<2^1/2b вектор B между точками перегиба на вогнутости направлен от наружной поверхности клетки вдоль оси z и внутрь клетки по оси x. Векторы магнитных моментов p_m каждого из ионов в фокусах, рассматриваемые вдоль оси x, образуют острый угол j. Направление B определяется кручением валентного электрона вокруг каждого из фокусов и в целом вокруг фокусов по часовой стрелке. Это соответствует правой паре прямых линий, но левой оптической активности – L-изомерам. Появляются токи смещения и rot H в диэлектрике, а, следовательно, чувствительность организма к малым изменениям магнитного поля. Малые изменения B во времени t (под крайне низкими частотами, < 3 – 30 Гц) обуславливают rot E и большие значения a независимо от тока. Возникает собственное магнитное поле организма – rot H в диэлектрической среде. Клетка становится органом восприятия электромагнитных полей и источником магнитного поля. Тупой угол j соответствует левой паре прямых линий, но правой оптической активности – D-изомерам.

Итак, чувствительность организма к электромагнитным полям, оптическая активность и магнетизм биосистем надо рассматривать с учетом микротоков в мембране на квантовом уровне.

ЛИТЕРАТУРА

1. Аветисов В.А., Гольданский В.И. // Успехи физических наук. 1996. Т. 166. №8. С. 873-891.

2. Казначеев В.П., Михайлова Л.И., Шурин С.П. Дистантное межклеточное взаимодействие в системе двух клеточных культур / Диплом открытия № 122 // БИ. 1973. № 19. С. 3.

3. Чизмаджев Ю.А. // Соросовский образовательный журнал. 2000. Т. 6. № 3. С. 23-27.

4. Регистрация одиночных каналов / Ред. Б. Сакмана и Э. Неера. М.: Мир, 1987.

5. Бронштейн В.Л., Исерович П.Г. // Криобиология. 1983. Т. 6. С. 22-24.

6. Antonov V.F., Petrov V.V., Molnar A.A. et al. // Nature. 1980. V. 283. P. 585-586.

7. Аносов А.А., Богатырева Н.Э., Антонов В.Ф. // Биофизика. 2000. Т. 45. №1. С. 65-68.

8. Берестовский Г.Н., Терновский В.И., Катаев А.А. // Там же. С. 69-78.

9. Wong A.Y.K., Classen G.A. // Ann. Biomed. Engng. 1995. V. 23. P. 822.

10. Регигер С.А., Шадрина Н.Х. // Биофизика. 2005. Т. 50. № 3. С. 515-536.

11. Александров П.С. Комбинаторная топология. М.-Л.: Гостехиздат, 1947.

12. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976.

THE FORMATION OF PORE IN BIOLOGICAL MEMBRANE THROUGH THE UNILATERAL SURFACE

Ch. A. Tukembaev

For formation of pore in a membrane the new unilateral surface is offered. The new unilateral surface as a body of rotation does not contain obvious self-crossings in three-dimensional space. Represents a diaphragm, i.e. is physical object, as Moebius's sheet and Klein's bottle. Transition in 4-dimensional space is replaced with torsion so, that the unilateral surface has points of an excess only in the center of symmetry where torsion changes a sign. New object as the diaphragm inside pore, explains formation of pore and the ionic channel in a biological membrane, optical activity and sensitivity of cells weak electromagnetic fields. The decision of a problem of optical activity of substance is based on a sign on torsion, i.e. determined by the right or left pair binormals.

Bibliography – 12 references

Кафедра прикладной информатики

Кыргызский государственный университет строительства, транспорта и архитектуры.

Поступила в редакцию 7.10.2007.

Автор: Тукембаев Чоро Абдылдаевич.

Старший преподаватель кафедры прикладной информатики Кыргызского государственного университета строительства, транспорта и архитектуры.

720020, Бишкек, ул. Малдыбаева, 34-б, Кыргызстан,

тел. +996(312) 549 223,

e-mail: choro@istc.kg

Department of applied computer science, Kyrgyz state university of construction, transport and architecture,

34 “b”, Maldybaev Str., Bishkek, 720020, Kyrgyz Republic,

tel.: +996(312) 549 223,

e-mail: choro@istc.kg