- Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 6. -
Вып. 4. - 2007. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/TITL-16.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/cont.htm
УДК
514.8+535.56+536.7
ЗНАЧЕНИЕ
ОРИЕНТИРОВАННОГО ОБЪЕМА ДЛЯ ОПТИЧЕСКОЙ АКТИВНОСТИ И ФАЗОВОГО ПЕРЕХОДА 3 РОДА
Ó
2007 г. Тукембаев Ч. А.
Фазовый переход 3 рода и оптическая активность зависят от якобиана в
элементе объема. Знак якобиана определяет положительность или отрицательность
элемента объема dV. Положительность dV соответствует D-изомеру, отрицательность dV – L-изомеру и равенство нулю – R-изомеру, т.е. рацемату.
Оптически активные вещества выражаются поверхностями 3 порядка и выше, но
оптически неактивное вещество – поверхностью 2 порядка. Это определяет роль
кручения молекулярных токов в знаке оптической активности, а отрицательную
кривизну надо рассматривать, учитывая знак кручения.
Фазовый переход 3 рода отвечает проницаемости замкнутой системы
термодинамики в открытую систему. Как не странно, аминокислоты живых существ
состоят из отрицательных элементов объема, что обуславливает их динамическую
активность. Полученный результат важен не только для понимания асимметрии живых
существ. Устойчивость термодинамического состояния приобретает новое значение
для изучения поведения вещества вблизи критической точки, так как
отрицательному элементу объема отвечает устойчивость на изотермах с
положительным наклоном, т.е. под спинодалью. В этой связи предлагается решить
вопрос с абсолютной отрицательной температурой в зависимости от L-частиц.
При условии, что сжимаемость –
трижды дифференцируемая функция градиента давления, решены и проблема
Пастера, и проблема фазового перехода 3 рода, которые
были связаны друг с другом. Это явилось следствием того, что в фазовом
переходе 3 рода вещество расщепляется по зеркальному признаку на L- и D-частицы и образуется солитон из частиц dV<0. Разные цвета в 2-цветном солитоне обусловлены частицами
противоположного знака.
Понимание сути отрицательного элемента объема и полученные результаты
необходимы в различных сферах науки для объяснения аномалий, а в технологиях –
для получения чистых веществ с новыми свойствами, очистки от примесей,
извлечения требуемых компонент в производстве лекарств, металлов, композитов,
полимеров и т.д.
Ключевые слова: оптическая
активность, кручение, ориентированный объем, L-изомер, D-изомер, R-изомер, критическая точка.
Введение
Возникновение и развитие
биоорганического мира основано на зеркально-асимметричной молекулярной
структуре. Для зеркальной асимметрии живой природы нет физико-химического объяснения
на молекулярном уровне. Не найдена причина оптической активности хиральных (D- и L-изомеров)
изомеров, что составляет суть проблемы Пастера [1, 2], (см. также приложение),
но ее состояние осталось неизменным [3]. Важность проблемы связана с асимметрическим
синтезом оптически чистых изомеров [4, 5], т.е. D- или L-изомеров,
что вызвано различным их действием на организм, т.е. токсичностью, в том числе,
рацематов – R-изомеров.
Для определения оптической чистоты и разделения оптических
изомеров используют хиральные сдвигающие элементы на основе лантаноидов,
ферментативный метод, методы двойного расщепления, газожидкостной
хроматографии, спектроскопии ядерно-магнитного резонанса и изотопного
разбавления. Способы формирования хирального избытка описаны в [6]. Среди этих
методов вращение плоскости поляризации света (ППС) остается главным
инструментом изучения асимметрии изомеров (см. приложение), так как его
чувствительность и точность выше на порядок. В решении проблемы не удается
связать знак оптической активности с молекулами, не обладающими явной винтовой
структурой, из-за недостатков теории [7-10], поэтому неясна причина вращения
ППС вправо (d) или влево (l) в молекуле. Почему живые
существа состоят только из D-аминокислот и L-углеводов
и в чем причина хирального избытка в них? Вероятно, хиральный избыток
формируется вблизи критической точки [11], но это фазовый переход, что
отрицается в [2]. В таком случае, разделение вещества в разные фазы должно
протекать по зеркальному признаку, что не принято в фазовых переходах 1 и 2
рода. Тогда, видимо, разделение вещества на D- и L-изомеры обусловлено фазовым
переходом 3 рода.
Путь к решению проблемы
наметился в [12], где за основу выбрана модель связанного осциллятора,
описываемого обыкновенным дифференциальным уравнением 3 порядка. Связанный
осциллятор учитывает силу трения Лоренца, как кручение молекулярных токов.
Простейшей моделью молекулярных токов двухатомной молекулы является линия
Кассини [13, 14] – прямой аналог распределения электронной плотности в молекуле.
В [13-15] оптическая активность молекулы обоснована кручением, правой и левой
парой прямых и смешанным произведением [(r1– r2)pq], что позволило найти условие, которому подчинен D-изомер
или L-изомер, т.е. d-
или l-вращение ППС. Знак [(r1– r2)pq] зависит от целого или дробного спина, магнитного момента одного из
изотопов молекулы. Однако [(r1– r2)pq] численно равно объему и имеет знак, но отрицательный объем не имеет
смысла в физике.
Сложность проблемы фазовых переходов 3 рода обусловлена трудностью
изучения вещества вблизи критической точки, на линии особых точек – спинодали,
а также трикритической точки с помощью теории Ландау [16]. Параметр порядка не
позволяет найти условия, которые приведут эксперимент к требуемому результату,
а картина фазового перехода зависит от излома и флуктуаций [17, 18]. Полевой
метод [19] с коррекцией поля Ландау на вероятные величины, которые стремятся к
точкам, где ¶3F/¶f3=0, ближе к решению, так как
средние величины определяются минимумом свободной энергии ¶F/¶f=0, f – флуктуирующая амплитуда
гидродинамической моды [20]. Если считать объем V модой, то в этом случае ¶3F/¶V3=–¶2P/¶V2=0, где P – давление, дает условие
критической точки [16]. Однако для фазового перехода 3 рода требуется скачок 3
производной термодинамического потенциала Гиббса G, но это не равносильно условию ¶3F/¶f3=0.
Согласно Эренфесту, фазовому
переходу 1 рода соответствует скачок 1 производной от G, фазовому переходу 2 рода –
скачок 2 производной и т.д. Термодинамика и статистическая физика не отрицают
существование фазовых переходов высшего порядка, например фазовых переходов 3
рода. Из-за крайней редкости фазовые переходы 3 рода экспериментально не
обнаружены [21], но, в дальнейшем, поставлены под сомнение [22]. Исследования
фазовых переходов [23-25], фазовых переходов 3 рода [26-31] на основе полевого
метода, Гинзбурга-Ландау не имели
успеха, однако в кластерах [25] возможно сосуществование фаз. Нет наглядных
примеров, кроме модификаций фазового перехода 2 рода на двумерной решетке
Изинга [16]. Трудности вызваны изучением изолированных и критических точек [16]
и, особенно, критических индексов [32] для изучения фазовых переходов. Однако
сложность решения некорректно подменять открытием нового явления [32, 33], так
как в метастабильной области рост объема понятен без открытия, а также
использовать отрицательную кривизну для получения решения [34]. Поэтому
проблема фазовых переходов – это магистральное направление в физике [35].
Необходимо вернуться к определению Эренфеста и напрямую решить проблему с привлечением
результатов из иных областей физики и математики. Это необходимо как для теории
фазовых переходов, так и для объяснения биологии законами физики [35] и
феноменов в природе. Объяснение зависит от решения проблемы Пастера [2],
которая за 10 лет осталась на прежнем уровне [3] из-за недостатка внимания к
фазовым переходам, солитонам [36] и 2-цветным солитонам в оптике [37], где
неясно отношение цвета к солитону.
Целью
настоящей работы является определение физической сути ориентированного объема в
оптической активности и фазовых переходах 3 рода и условий, обуславливающих
градиент давления в трансформации замкнутой системы термодинамики в открытую
систему.
2. Результаты и обсуждение
2.1.Оптическая активность
Лемма.
В правой системе координат xyz
знак оптической активности соответствует знаку якобиана измеряемого элемента
объема dV=g1/2dx1dx2dx3 для поверхностей 3 порядка
и выше или знаку кручения.
Доказательство. Элемент объема в области H
определяется по формуле
![]()
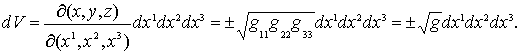 (1)
(1)
Знак плюс берется в правой системе координат x1x2x3, когда Det (g)>0, но знак минус
выбирается в случае левой системы координат x1¢x2¢x3¢, когда определитель g<0. Обе системы координат
образованы направляющими векторами касательной t, главной нормали n и
бинормали b триэдра Френе. Направление
оси вращения определяется вектором Дарбу W=tt+kb.
Векторы t, n и b удовлетворяют формулам
Френе-Серре
t¢=kn, n¢=-kt+tb, b¢=-tn,
где кривизна k=|t¢|=|r²| не может быть отрицательной
величиной по определению, кручение t=k-2[r¢r²r¢²] зависит от смешанного
произведения производных r¢, r² и r¢² [38].
Элементу объему dV>0 соответствует
положительная ориентация параллелепипеда, где положительно ориентирован
упорядоченный набор векторов x1, x2, x3, но отрицательному элементу
объема dV<0 – отрицательная
ориентация, где ориентация определяется левой тройкой векторов x1¢, x2¢, x3’. Когда dV=0, то векторы x1, x2, x3 или x1¢, x2¢, x3¢ линейно зависимы. Исходя из
определения объема, как тройного интеграла, для алгебраических поверхностей 2
порядка, например сферы, получаем dV=0.
Значит, ориентированный элемент объема возможен только для поверхностей 3
порядка и выше, которые позволяют рассматривать кручение, и представляет
бесконечно малую область, содержащую частицу – молекулу, с центральной точкой V0, относительно которой
возникает ориентация частицы.
Так как рассматриваемая
область H определяется правой
системой координат xyz,
то в случае g>0 измеряемый элемент
объема dV>0 одинаково ориентирован
с правой системой координат xyz.
Если детерминант g<0, то ориентация
измеряемого элемента объема dV<0
противоположна правой системе координат xyz. Значит, внутрь области H помещен отрицательный элемент объема dV с левой тройкой векторов x1¢, x2¢, x3¢.
Для инверсии ориентации,
казалось бы, достаточно поменять местами x1 и x2 в правой тройке векторов x1, x2, x3. Тогда получается левая
тройка векторов x1¢, x2¢, x3¢. Однако геометрия элемента
объема определяется d-
или l-вращением триэдра Френе,
т.е. движением молекулярных токов. Если векторы t, n и b образуют правую тройку
векторов, согласно вектору Дарбу, то имеем правую систему x1x2x3, но для левой тройки
векторов t, n и b получаем левую систему x1¢x2¢x3¢ Примером является правая
или левая винтовая линия.
Правая и левая пара
скрещивающихся неперепендикулярных прямых L1 с направляющим вектором p и L2 с направляющим вектором q однозначны принципам
измерения оптической активности. Прямые L1 и L2 лежат в плоскости вращения
ППС, причем L1 с направляющим вектором p принадлежит поляризатору,
но L2 с вектором q – анализатору так, что L1 находится между началом
координат и прямой L2. Направляющие векторы p и q физически отождествляются
вектором напряженности электрического поля и лежат в плоскости поляризации
света. Измеряемый элемент объема, который содержит вещество, находится между
прямыми L1 и L2.
Правой паре соответствует
кратчайший поворот прямой L1 против часовой стрелки в
положение, параллельное прямой L2. Значит, такой поворот
однозначен вращению анализатора по часовой стрелке, а потому измеряемый элемент
объема относится к D-изомерам. Левой паре прямых соответствует
кратчайший поворот прямой L1 по часовой стрелке в
положение, параллельное прямой L2. Поэтому левая пара
определяет l-вращение ППС, так как
анализатор приходится вращать против часовой стрелки, т.е. влево.
Следовательно, измеряемый элемент объема относится к L-изомерам. Для прямых L1 и L2, лежащих в одной плоскости
или перпендикулярных друг другу, т.е. линейно зависимых векторов x1, x2, x3, вращение ППС неопределенно
и соответствует оптически неактивным средам, т.е. рацематам [15].
Кратчайшему расстоянию d между парой прямых L1 и L2 соответствует расстояние, пройденное
светом в оптически активном веществе. Правая пара и левая пара определяются
знаком d. Знак d определяется по известной
формуле
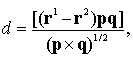 (2)
(2)
где r1 – радиус-вектор точки P, откуда берет начало
направляющий вектор p прямой
L1, r2 – радиус-вектор точки Q – начало направляющего
вектора q прямой L2 и (r1– r2) – радиус-вектор с началом в точке P и концом в точке Q.
Векторы p и q приведем к общему началу.
Тогда смешанное произведение [(r1– r2)pq] численно равно элементу объема dV параллелепипеда, построенного на векторах (r1–r2), p и q, т.е. формула (1)
представляет ориентированный элемент объем параллелепипеда dV=[(r1– r2)pq]. Поэтому dV
определяется знаком [(r1– r2)pq] и ориентацией векторов t, n и b триэдра, т.е. кручением
молекулярных токов. Если смешанное произведение [(r1– r2)pq]>0, то система (r1–r2), p, q – правая dV>0 и образует правую пару
прямых, но, если [(r1– r2)pq]<0, то система (r1–r2), p, q – левая dV<0 и образует левую пару.
Для компланарных векторов (r1–r2), p, q элемент объема dV=0, так как [(r1– r2)pq]=0 .
Сравним формулу (2) с
формулой отклонения
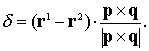 (3)
(3)
В случае правой пары точка Q и начало координат лежат по
разные стороны от плоскости, определяемой векторным произведением p´q, поэтому d>0. Иначе, между
векторами p и q находится элемент объема dV>0. Для левой пары точка Q и начало координат лежат по
одну сторону от плоскости, но отклонение d<0, так как определяется
отрицательным знаком модуля |p´q|=|p|×|q|sinj, когда j>p. Но "j>p кратчайший поворот прямой L1 в положение, параллельное
прямой L2, совершается по часовой
стрелке, т.е. анализатор приходится вращать влево. Здесь можно приписать
отрицательный знак |p´q| вектору (r1–r2), тогда отклонение d определяется смешанным произведением (r1– r2)(p´q). Значит, отклонению d<0 соответствует вектор (r2– r1), а потому получаем
зеркальное отражение объекта, представленного точкой Q, когда внутрь области H, между векторами p и q, помещен отрицательный
элемент объема dV<0.
Таким образом, знак
оптической активности однозначен знаку dV=[(r1– r2)pq], а в случае компланарных векторов (r1–r2), p, q равенство [(r1– r2)pq] нулю соответствует рацематам. Причем, отрицательное отклонение в
формуле (3) в явном виде указывает на зеркальное отражение объекта, а
ориентация триэдра Френе – на кручение молекулярных токов. Следовательно, D-изомеру
соответствует dV>0, L-изомеру
– dV<0, а рацемату – dV=0,
что и требовалось доказать. ■
2.2. Фазовый переход 3 рода
В работах [13, 14]
предложено решение, в котором фазовый переход связывается с трансформацией
замкнутой системы термодинамики в открытую систему на основе обобщенной
восприимчивости [16]. Решение подкреплено примерами из реологии для
биологической мембраны и горных пород. Необходимым фактором служит эластичность
мембраны и дилатансия пород, где образование поры трансформирует замкнутую
систему в открытую систему [14]. Открытая система подразумевает
полупроницаемость мембраны, т.е. существование в ней пор и градиента давления.
Необходимо найти условия, при которых возникает градиент давления. Фазовый
переход 3 рода дает возможность преобразовать замкнутую поверхность в тор, т.е.
получить пору. Это обусловлено тем, что коэффициенты обобщенной восприимчивости
аналогичны коэффициентам Онзагера и вблизи критической точки связывают
параметры термодинамической системы с флуктуациями нетермодинамических
параметров электромагнитного поля [16].
|
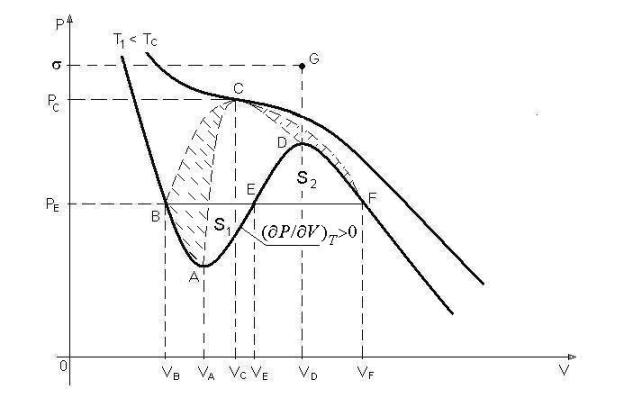
Рис. Изотермы реального
газа. |
|
Метастабильная область
между бинодалью BCF
и спинодалью ACD заштрихована. Под
спинодалью находится область неустойчивых состояний. Отмечена изотерма с
положительным наклоном (¶P/¶V)T>0 на участке AED. Остальные участки
изотермы имеют отрицательный наклон (¶P/¶V)T<0. В критической точке C
на критической изотерме TC соприкасаются области устойчивых и неустойчивых состояний и
метастабильная область. |
Для решения вопроса примем
за основу теорию Ландау и изучим характер особенностей линии особых точек [16]
на бинодали BCF, на спинодали ACD и под спинодалью (рис.).
Системы биологии, геологии, гидродинамики и реологии объединяет дилатансия DV=V–VD. Упругость горных пород,
эластичность мембраны определяются пределом прочности s в точке G, где удлинение-расширение объема V до значения VD происходит без разрушения материала.
Точки B и F расположены на
границе метастабильного состояния и через них проходит экспериментальная
изотерма реального газа, поэтому участок BF фактически является изобарой на такой
изотерме. Из точки B жидкость превращается в газ, как следствие скачка в точку F, или в
метастабильную жидкость, переходя по изотерме в точку A. Тогда переход
по изотерме в точку A связан с изменением свободной энергии, но в точку F – с фазовым
переходом, так как на изобаре BF потенциал G претерпевает скачок. В точке F возникает конденсация газа, откуда
возможно превращение в жидкость вдоль изобары BF или в метастабильный газ при
изотермическом сжатии в точку D. Значит, точки B и F являются точками бифуркации – раздвоения на энергию F вдоль изотермы
и потенциал G по изобаре, где возможно сосуществования фаз [25].
Теорема. Если сжимаемость b=-V0-1dV/dP на изотерме реального газа
трижды дифференцируемая функция в точке перегиба V0, то данная точка является единственной точкой
фазового перехода 3 рода и порождает солитон в области неустойчивых состояний.
Доказательство. На основе формулы (1) считаем, что dV>0. Для термодинамического
равенства требуется выполнение условий [16, c. 567-568]
¶2P/¶V2=0, ¶3P/¶V3<0. (4)
Данное условие частный случай того, что в точке
перегиба все производные четного порядка равны нулю [38]. Результаты, полученные в
[20], явились следствием ¶2P/¶V2=0. Если к неравенству (4)
присоединить условие ¶P/¶V=0, то получим критическую
точку C в ее классическом смысле
[16]. Такая критическая точка является точкой перегиба, в которой
¶P/¶V=¶2P/¶V2=0, ¶3P/¶V3<0. (5)
Однако точки перегиба не исчерпываются условиями (4)
и (5). Дополнив условие (4) неравенством ¶P/¶V<0, получим на бинодали точки
перегиба B и F, в
которых
¶P/¶V<0,
¶2P/¶V2=0, ¶3P/¶V3<0. (6)
В области неустойчивых состояний точка перегиба E определяется условиями
¶P/¶V>0,
¶2P/¶V2=0, ¶3P/¶V3>0. (7)
Условие (6) справедливо для устойчивых состояний реального
газа и позволяет изучать сжимаемую жидкость. Условие (5) отвечает несжимаемой
жидкости.
Для сжимаемости b=-V0-1dV/dP в
точке перегиба V0, не делая никаких
предположений о знаке dV, с учетом ¶2V/¶P2=¶4V/¶P4=0 и ¶P/¶r=c2 находим
производные:
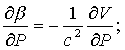 (8)
(8)
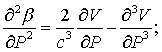 (9)
(9)
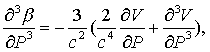 (10)
(10)
где c2=¶P/¶r – это квадрат местной скорости звука в локальном
объеме вокруг точки V0, так как r=V0-1 – плотность
газа в малой окрестности точки V0.
В точке перегиба производная
db/dP=-c-2dV/dP это 3 производная от потенциала G: db/dP=(-V0-1(¶3G/¶P3)). Поэтому потенциал G для элемента объема dV есть химический потенциал m одной частицы, по энергии
равный уровню Ферми, так как b трижды дифференцируемая
функция, но P=-(¶E/¶V)S требует вычисления
производных по 3 координатам, где E –
энергия, S – энтропия. Для фазового
перехода 3 рода необходим скачок db/dP. Исключим правую часть системы (8)-(10) и относительно db/dP получим обыкновенное дифференциальное уравнение 3 порядка с
постоянными коэффициентами
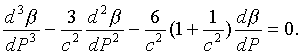 (11)
(11)
В уравнении (11)
c2=¶P/¶r>0, так как dV>0 в точке перегиба B или F. Уравнению (11) соответствует условие (6) и характеристическое уравнение, один корень которого q0=0 (изолированная точка).
Остальные корни квадратного уравнения действительные, различные и разного знака
для всех скоростей c>0 описывают странный
аттрактор (особая точка типа седло) в зависимости от градиента давления dP. Это обуславливает
отталкивание частиц – квантовый эффект
[16] в метастабильной области, поэтому объем растет в опытах [32, 33] и не
может быть новым явлением. Так как градиент давления вызывает осмотическое
давление [16], то замкнутая система термодинамики становится проницаемой и
превращается в открытую систему.
Химический потенциал m частицы – молекулы определяется знаком
якобиана в формуле (1), т.е. знаком dV. Химический потенциал нулевой частицы m0=0 соответствует q0=0 и следует из dV=0, а это геодезическая линия
нулевой длины – траектория светового луча [38]. Такая частица излучает фотон, а
в фазовом переходе обуславливает критическую опалесценцию. Элементу объема dV>0 соответствует m2>0, а частица с таким
химическим потенциалом является бозоном. Тогда частица dV<0 будет фермионом, так как ее химический потенциал m1<0.
Под спинодалью, т.е. в
области неустойчивых состояний, а это изотерма с положительным наклоном (¶P/¶V)T>0, в точке перегиба E выполняются условия (7). Устойчивым состояниям на такой изотерме
отвечают только частицы dV<0, а это L-частицы. После подстановки отрицательного значения dV в условие (7)
получим условие (6), определяющее устойчивое состояние. В тоже время, все
частицы dV>0, но это D-частицы,
будут неустойчивыми. Тогда поведение L-частиц
описывается уравнением
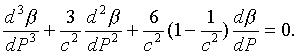 (12)
(12)
Уравнение (12) получено из
уравнения (11) переменой знаков при коэффициентах, так
как ¶P/¶r=–c2<0
для "dV<0. Уравнению (12) соответствует
характеристическое уравнение, один корень которого q0=0. Остальные корни q1, q2 будут комплексными корнями,
если c>(1.375)1/2.
Это справедливо как для сверхзвуковой скорости, где db/dP=(-V0-1(¶3G/¶P3)), так для и групповой скорости u>(1.375)1/2c, где c – скорость света, так как d3b/dP3 соответствует пятой производной ¶5G/¶P5. Элемент объема dV в случае db/dP содержит гидродинамическую частицу в малой окрестности точки V0, но для d3b/dP3 – квантовую частицу в точке V0. Для получения квантовой частицы
необходимо сжать молекулярный объем так, чтобы распределенная плотность газа
была сосредоточена в точке V0, т.е. трижды
продифференцировать сжимаемость b или объем. Значит, фазовый переход
3 рода является границей между макрочастицами и квантовыми частицами,
разделенных условием ¶4V/¶P4=0.
Случай комплексных корней
дает устойчивый фокус и уравнение (12) описывает стационарную волну
сжимаемости, зависящую от dP.
Действительные отрицательные корни и устойчивый узел получаем для скорости u<c, поэтому волна сжимаемости
монотонно затухает. Устойчивому фокусу и устойчивому узлу соответствуют в
начале координат односторонние производные, что определяет скачок искомой db/dP, т.е. скачок ¶3G/¶P3.
Отрицательные элементы
объема dV<0 являются в клетке L-аминокислотами, а это
следует из леммы и [15]. Химический потенциал L-аминокислот m<0, поэтому их отличает высокая химическая
активность, устойчивое состояние под спинодалью, чем поддерживается динамика в
клетке, но в зависимости от градиента давления.
Рассматривая уравнение (12)
на временном интервале, получим следующее уравнение
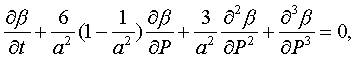
аналогичное солитону. Так как уравнение (12)
получено в области неустойчивых состояний для частиц с объемом dV<0, то
наблюдение таких частиц, солитонов требует редкого сочетания условий в природе.
Именно в такие условия попал Рассел, наблюдая солитон. Значит, под спинодалью существует
точка перегиба на изотерме, которая является единственной точкой фазового
перехода 3 рода и порождает солитон из частиц dV<0. Движение солитона является направленным, согласно
градиенту давления, устойчивому фокусу или узлу, поэтому движение L-частиц
означает переход в новую фазу.
Для
искусственного создания сочетания условий необходимо понимание физической сути
отрицательного элемента объема, его устойчивости в области абсолютно
неустойчивых состояний. Тогда эксперимент будет многократно повторяемым не
только в гидродинамике, но и в оптике, где цвет солитона определяется знаком dV<0. Главным
следует считать то, что система (8)-(10) получена из основного уравнения
термодинамики и фазовый переход 3 рода трансформирует замкнутую систему
термодинамики в открытую систему.
Итак, расщепление вещества
на частицы с разными по знаку химическими
потенциалами m0, m1 и m2 и движение частиц
противоположного знака в разные фазы зависит от
градиента давления. Так как в разных фазах частицы с потенциалами m0, m1 и m2 удовлетворяют условию равновесия фаз: |m1|=m2, то это фазовый переход. Тем более,
это фазовый переход 3 рода в силу разделения частиц по зеркальному признаку и
скачка искомой db/dP, т.е. скачка третьей производной ¶3G/¶P3 термодинамического потенциала G. Теорема доказана. ■
Заключение
Таким образом, фазовый переход
3 рода и оптическая активность зависят от якобиана в элементе объема. Знак
якобиана определяет положительность или отрицательность элемента объема.
Доказанная лемма ставит положительный элемент объема в соответствие D-изомеру,
отрицательный элемент объема – L-изомеру и нулевой элемент
объема – R-изомеру, т.е. рацемату. Оптически активные вещества
выражаются поверхностями 3 порядка и выше, но оптически неактивное вещество –
поверхностью 2 порядка. Это определяет роль кручения молекулярных токов в знаке
оптической активности, а отрицательную кривизну надо рассматривать, учитывая
знак кручения.
Фазовый переход 3 рода
отвечает случаю проницаемости замкнутой системы термодинамики в открытую
систему. Полученный результат важен не только для понимания асимметрии
биоорганического мира, где, как не странно, аминокислоты живых существ состоят
из отрицательных элементов объема, что обуславливает их динамическую активность
в виде колебаний. Устойчивость термодинамического состояния приобретает новое
значение для исследований вблизи критической точки, так как отрицательному
элементу объема отвечает устойчивость на изотермах с положительным наклоном,
т.е. под спинодалью. Поэтому надо пересмотреть понятие абсолютной отрицательной
температуры с учетом левых L-частиц.
При условии, что сжимаемость
– трижды дифференцируемая функция
градиента давления, решены и проблема Пастера, и проблема фазового перехода 3
рода, которые оказались связанными. Это явилась следствием того, что в фазовом
переходе 3 рода вещество расщепляется по зеркальному признаку на L- и D-частицы
и образуется солитон из отрицательных частиц dV<0. Разные цвета обусловлены частицами
противоположного знака в 2-цветном солитоне. Фазовый переход 3 рода является
границей между макрочастицами и квантовыми частицами, разделенных условием ¶4V/¶P4=0.
В веществе преобладают
частицы dV>0,
которые представлены изотопами, в основном, с нулевым спином, а также с
целочисленным спином. Малая доля частиц dV<0 в веществе обусловлена изотопами с дробным спином, т.е.
фермионами, а это диспропорция в зеркальной асимметрии отражает реальное
соотношение между L- и D-частицами. Понимание сути
отрицательного элемента объема и полученные результаты необходимы в различных
сферах науки для объяснения аномалий, а в технологиях – для получения чистых
веществ с новыми свойствами, очистки от примесей, извлечения требуемых
компонент в производстве лекарств, металлов, композитов, полимеров и т. д.
Список литературы
1.
Кизель
В.А. Физические причины дисимметрии
живых систем. М.: Наука, 1985. 120 с.
2.
Аветисов
В.А., Гольданский В.И. Физические аспекты нарушения зеркальной симметрии
биоорганического мира // Успехи физических наук. 1996. Т. 166. № 8. С. 573-591.
3.
Островский
В.Е., Кадышевич Е.А. Обобщенная гипотеза происхождения простейших элементов
живой материи, трансформации первичной атмосферы и образования залежей гидрата
метана // Там же. 2007. Т. 177. № 2. С. 183-206.
4.
Williams K., Lee E. Importance
of drug enantiomers in clinical
pharmacology // Drugs. 1985. Vol. 30. P. 333-354.
5.
Dunina V.V., Beletskaya I.P. Homogeneous
Catalysis by Optically-Active Complexes of Transition-Metals and its
Application in The Synthesis of Bioactive Molecules. 3. Oxidation // Zhurnal
Organicheskoi Khimii. 1993. V. 29 (4). P. 806-878. (Russian).
6.
Яблоков M.Ю., Иванов
В.Ф., Грибкова О.А. и др. Структурно-обусловленная оптическая
активность в пленках полианилина // Исследовано в России. 2004. С. 1577-1585.– http://zhurnal.ape.relarn.ru/articles/2004/145.pdf
7.
Glazer A.V., Stadnicka K. On the Origin of
Optical Activity in Crystal Structures // J. Appl. Cryst. 1986. V.19. P.
108-122.
8.
Devaragan V., Glazer A.V. Theory and
computation of optical rotatory power in inorganic crystal // Acta Cryst. 1986.
V. A42. P. 560-569.
9.
Vekstein G. E. On the natural optical activity
in an isotropic medium: An exactly solvable model // Am. J. Phys. 1996. N 64. P. 607–610
10.
Калдыбаев
К.А., Константинова А.Ф., Перекалина З.Б. Гиротропия одноосных поглощающих
кристаллов / Ин-т кристаллографии им. А.В. Шубникова РАН. М.: 2000. 300 с.
11. Kondepudi D.K., Nelson G.W. Weak neutral currents
and the origin of biomolecular chirality // Nature. 1985. Vol. 314. P. 438-441.
12.
Тукембаев
Ч.А., Валуйский П.П., Васильев И.А. и др. Решение задачи о вращении плоскости
поляризации света // Вестник Инженерной академии наук Республики Казахстан.
2001. № 1(6). С. 52-56.
13.
Тукембаев Ч.А. Фазовый переход при образовании солитонов и
трансформации замкнутой системы термодинамики в открытую систему //
Физико-химический анализ многокомпонентных систем. 2007. Вып. V. URL: http://kubstu.ru/fh/fams/st25.doc
14.
Тукембаев Ч.А. Образование поры в биологической мембране сквозь одностороннюю
поверхность // Математическая морфология. 2007. Т.6. Вып.4. URL: http://www.smolensk.ru/user/sgma/MMORPH/N-16-html/tukembaev-1/tukembaev-1.htm
15.
Тукембаев Ч.А. Гипертермия, митогенетическое излучение и
зеркальные изомеры в проблеме рака // Там же. Вып.3. URL: http://www.smolensk.ru/user/sgma/MMORPH/N-15-html/tukembaev/tukembaev.htm
16.
Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Ч.
1. М.: Наука, 1995. 608 с.
17.
Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых
переходов. М.: Наука, 1982. 381 с.
18. Domb C. The critical point. London: Taylor &
Francis, 1996. 376 p.
19. Zinn-Justin J. Quantum Field Theory and Critical Phenomena. Oxford:
Clarendon Press, 1994. 996 p.
20.
Олемской
А.И., Бражный В.А. Полевая теория флуктуаций при фазовых переходах // Физика
твердого тела. 1999. Т. 41. Вып. 9. С. 1689-1692.
21.
Базаров
И.П. Термодинамика. М.: Высшая шк., 1976. 447 с.
22.
Bazarov I.P., Bondarenko V.V. On the
impossibility of the third and higher order phase transitions // J. Phys. Chem. (Russia). 1996. V. 70. N. 7. P. 1198-1200.
23.
Берри
Р.С., Степанов Б.М. Фазовые переходы и сопутствующие явления в простых системах
связанных атомов // Успехи физических наук. 2005. Т. 175. № 4. С. 368-411.
24.
Коршунов
С.Е. Фазовые переходы в двумерных системах с непрерывным вырождением // Там же.
2006. Т. 176. № 3. С. 234-274.
25.
Смирнов
Б.М. Кластеры и фазовые переходы // Там же. 2007. Т. 177. № 4. С. 369-373.
26. Gross D.J., Witten E. Possible third-order phase transition in the large-N
lattice gauge theory // Phys.
Rev. D. 1980. V. 21. P. 446-453. http://link.aps.org/abstract/PRD/v21/p446
27. Eisele T. On a third-order phase transition //
Communic. in Mathem. Phys. 1983. V.90. N.1. P.125-159.
28. Azakov P. I. One-plaquette (2+1)-model with
arbitrary action // Theoretical
and Mathematical Physics. 1985. V.62. N.2. P.
222–235.
29. Alimohammadi M., Khorrami M. On the phase structure of
two-dimensional generalized Yang-Mills theories // Nucl.
Phys. 2001. B597. P. 652-661.
30. Cronström C., Noga M. Third-order Phase Transition and Superconductivity in Thin Films //
Czechoslovak J. Phys. 2001. Vol. 51, N. 2, P. 175-184.
31. Li L. and Meurice Y. Is there a third-order phase transition in quenched
OCD? // Proceedings of Science XXIIIrd
International Symposium on Lattice Field Theory. 25-30 July 2005. Trinity
College, Dublin, Ireland. P. 258/1-258/6. http://arxiv.org/pdf/hep-lat/0507034
32.
Иванов Д.Ю. Поведение критических индексов в ближайшей
окрестности критической точки неидеализированных систем // Докл. РАН. 2002. Т.
383. № 4. С.478-481.
33.
Иванов Д.Ю. Феноменологическая модель критического поведения
реальных систем // Там же. 2004. Т. 394. №
6. С. 757-760.
34.
Жуховицкий Д.И. Поверхностное натяжение границы раздела
пар-жидкость с конечной кривизной // Коллоидный журнал. 2003. Т. 65. № 4. С.
480-494.
35.
Гинзбург
В.Л. О физике и астрофизике. М.: Наука, 1985. 400 с.
36. Маневич Л.И., Савин А.В.,
Смирнов В.В. и др. Солитоны в невырожденных бистабилъных системах // Успехи
физических наук. 1994. Т. 164. № 9. С.
937-958.
37.
Simos C., Couderc V., Barthelemy A. et al. Phase-dependent
interactions between three-wave spatial solitons in bulk quadratic media // J. Opt.
Soc. Am. B. 2003. V. 20. P. 2133-2141.
38.
Корн
Г, Корн Т. Справочник по математике. М.: Наука, 1984. 832 с.
Приложение
В последние несколько лет в
МГУ развивается новое направление в "классической" нелинейной оптике,
остававшееся до последнего времени практически не затронутым ни теоретическими,
ни экспериментальными исследованиями. Речь идет о новом круге
нелинейно-оптических явлений в изотропных средах с нарушенной зеркальной
симметрией (прежде всего - в жидких растворах зеркально-асимметричных
(хиральных) молекул), составляющих нелинейный аналог эффектов естественной
оптической активности в таких же средах. Этот казалось бы весьма частный вопрос
физики нелинейных оптических процессов приобретает актуальность и
междисциплинарную значимость в связи с выработкой новых подходов к изучению
удивительного феномена живой природы на молекулярном уровне, получившим
название "хиральной чистоты" биоорганического мира. По пока
невыясненным причинам, живая природа "предпочитает" выбирать в
качестве элементарных молекулярных кирпичиков только один из двух возможных
зеркальных стереоизомеров органических молекул ("правых" или
"левых"): все молекулы углеводов - сахаров, входящих в живые
организмы или представляющих продукты их жизнедеятельности, являются
"правыми" изомерами, а молекулы аминокислот, напротив, - только
"левыми" изомерами и т. п. Эта открытая еще Л.Пастером
фундаментальная зеркальная асимметрия живой природы на молекулярном и
надмолекулярном уровне до сих пор не нашла своего объяснения в рамках
физико-химических представлений. Однако, наличие глубокой связи между
зеркально-асимметричной структурой молекулярной основы жизни и возникновением и
развитием биоорганического мира в настоящее время не вызывает сомнений. Одним
из главных физических инструментов изучения этого феномена живой природы была и
пока остается спектроскопия оптической активности жидких растворов
биоорганических молекул. Однако, целый ряд фундаментальных ограничений этого
метода "линейной" оптической спектроскопии не позволяют с его помощью
продвинуться сколько-нибудь далеко в решении упомянутой фундаментальной
проблемы. Недавно удалось показать, что своеобразно протекающие в таких средах
нелинейные оптические процессы могут быть положены в основу нового типа
оптической спектроскопии с многообещающими перспективами в области изучения
молекулярной хиральности. Речь идет о таких новых явлениях, как электровращение
плоскости поляризации световой волны, круговой электродихроизм, оптическое
выпрямление, циркулярный фотогальванический эффект, генерация суммарных и
разностных оптических частот в объеме и на поверхности диссимметричных
жидкостей, и другие нелинейно-оптические эффекты, описываемые
электро-дипольными оптическими восприимчивостями четного порядка
(отсутствующими в центросимметричных жидкостях и рацемических растворах);
нелинейная оптическая активность, круговой дихроизм двухфотонного поглощения
света, и другие. Исследовательская активность в этом направлении стремительно
нарастает во многих лабораториях мира. Ряд ведущих конференций по нелинейной
оптике и применениям лазеров в науках о жизни уже ввели в свои программы
разделы по нелинейным оптическим явлениям в средах с нарушенной зеркальной
симметрией. Некоторые из предсказанных эффектов уже экспериментально
обнаружены, другие еще ждут проверки экспериментом. Но уже сейчас ясно, что
новые нелинейные оптические явления в сочетании с современной фемтосекундной
лазерной техникой способны существенно обновить всю область изучения
молекулярной хиральности, и через нее - изучение феномена нарушения зеркальной
симметрии в биоорганическом мире.
Профессор Н.И.
Коротеев, физический факультет МГУ
THE
VALUE OF ORIENTATION OF VOLUME FOR OPTICAL ACTIVITY AND Third-order Phase transition
Tukembaev Ch. A.
The third-order phase transition and
optical activity depend from the Jacobian in an element of volume. The
Jacobian's sign determines positivity or negativity of an element of volume dV. The positivity
dV correspond to a D-isomer, the negativity dV – L-isomer and equality to zero – R-isomer
(racemate). Optically active substances are expressed by surfaces 3 orders and
above, but optically inactive substance - a surface 2 orders. It defines a role
of torsion of molecular currents in a sign of optical activity, and negative
curvature should be investigated with a sign of torsion.
The third-order phase transition
causes the transmittivity of the closed system of thermodynamics in the open
system and gives boundary between macroparticles and quantum particles. Amino
acids of alive essences consist of negative elements of volume, and it causes
their dynamic activity. The received result is important not only for an
essence of asymmetry of alive essences. Stability of a thermodynamic condition
gets new value for studying behaviour of substance near to a critical point.
The negative element of volume gets stability on isotherms with positive
declination. In this connection it is necessary to reconsider a question on
absolute negative temperature depending on L-particles.
Provided that the compressibility – three times differentiated function of a gradient
of pressure, are solved also Pasteur's problem, and a problem of third-order phase transition which have been connected with each other. The substance is
split to a mirror attribute on L- and D-particles in
the third-order phase transition,
therefore is formed the soliton of particles dV<0. Different colors in 2-color soliton are
caused by particles of an opposite sign.
The understanding of an essence of a negative
element of volume and the received results are necessary in various spheres of
a science for an explanation of anomalies, and in technologies – for
manufacture of pure substances with new properties, scavenging in manufacture
of medicines, metals, composites, polymers, etc.
Keywords: optical activity,
torsion, orientation of volume, L-isomer, D-isomer, R-isomer, critical point.
Pages – 10, figures – 1, bibliography – 38 references.
Department of applied computer science,
Kyrgyz state university of construction, transport and architecture,
34 “b”, Maldybaev Str., Bishkek, 720020, Kyrgyzstan,
tel.: +996(312) 549 223,
e-mail: choro@istc.kg
Автор: Тукембаев Чоро Абдылдаевич.
Кыргызский
государственный университет строительства, транспорта и архитектуры, кафедра
прикладной информатики, старший преподаватель,
720020, Бишкек, ул.
Малдыбаева, 34-б, Кыргызстан,
тел. +996(312) 549 223, e-mail: choro@istc.kg
Кафедра прикладной информатики
Кыргызский государственный университет строительства, транспорта и архитектуры.
Бишкек, Кыргызстан
Поступила в редакцию 17.11.2007.