Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 7. -
Вып. 1. - 2008. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-17-html/TITL-17.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-17-html/cont.htm
УДК
621.396.969
Оптимальные по
критерию минимума средних квадратов алгоритмы
формирования радиолокационных изображений
групповых аэродинамических объектов
Ó
2008 г. Вашкевич С. А.
В
статье разрабатываются оптимальные по критерию минимума средних квадратов
ошибки алгоритмы формирования радиолокационных изображений групповых аэродинамических
объектов. В основе синтеза этих алгоритмов лежит теория статистического оценивания.
Ключевые слова: радиолокационное
изображение; оптимальный алгоритм; критерий минимума СКО.
Одним из перспективных направлений расширения информационных возможностей
современных РЛС зенитных комплексов является радиовидение [1]. Это направление
позволяет формировать радиолокационные изображения (РЛИ) объектов, находящихся
в зоне облучения РЛС. Для получения РЛИ применяются различные методы, но
наибольшую популярность из них приобрел метод инверсного синтезирования
апертуры антенны. В свое время формированием РЛИ аэродинамических объектов на основе
этого метода занимались Я. Д. Ширман, А. Я. Пасмуров,
Ю. С. Зиновьев, Б. Д. Стайнберг, Н. Х. Фархат,
А. А. Манукян, Д. Г. Митрофанов и др [2 – 7]. Однако
все разработанные ими способы базировались на детерминированном подходе к
задаче формирования РЛИ, в основе которых лежали оценки параметров отраженного
сигнала, полученные при очень больших отношениях сигнал-шум. Другие же задачи
радиолокационного наблюдения такие как обнаружение, измерение координат и параметров
движения, разрешения объектов традиционно рассматривались с позиций
стохастического подхода, а в результате их решения синтезировались оптимальные
по одному из критериев алгоритмы. Возникает вопрос, связанный с возможностью
разработки стохастических алгоритмов формирования РЛИ в рамках метода
инверсного синтезирования апертуры антенны. К тому же стохастические алгоритмы
формирования РЛИ существуют и довольно успешно применяются в бортовых РЛС с
прямым синтезированием апертуры антенны [1]. Но эти алгоритмы не совсем пригодны
для непосредственного применения в РЛС зенитных комплексов в виду ряда специфических
особенностей наблюдения аэродинамических объектов, в том числе и групповых [8].
Таким образом, целью настоящей статьи является
разработка оптимальных по критерию минимума средних квадратов (МСК) ошибки алгоритмов
формирования РЛИ групповых объектов, использующих цифровой инверсный синтез
апертуры антенны.
Перед тем как приступить к синтезу оптимальных
алгоритмов, необходимо выяснить физический смысл РЛИ. В радиолокации
повсеместно используется способность реальных объектов отражать (рассеивать)
падающую на них электромагнитную энергию. Но особенность РЛИ заключается в том,
что оно должно соответствовать положению отражающих объектов в пространстве, а
поскольку при инверсном синтезировании используются двумерные РЛИ, то – на
плоскости.
В математической модели сигнала, отраженного от
групповой цели, [8] способность объектов рассеивать электромагнитные волны
описывалась с помощью двумерной функции радиолокационного рассеяния (РЛР) 
. Для удобства понимания
дальнейших преобразований целесообразно привести вид модели отраженного сигнала
[8]:
, (1)
где 
– функция
радиолокационного рассеяния [9]; 
– ядро
интегрального преобразования, соответствующее сигналу на выходе оператора L
при воздействии на его вход функции радиолокационного рассеяния (РЛР) в виде
единичного дельта-импульса с координатами 
, т. е. одного элементарного (точечного) отражателя.
Из выражения (1) следует, что отраженный сигнал
получен в результате линейного интегрального преобразования функции РЛР. В
теории линейных систем подобное преобразование рассматривается как решение «прямой»
задачи анализа, когда находится отклик фильтра с известной импульсной
характеристикой на заданное входное воздействие. Тогда под «обратной» задачей следует понимать нахождение неизвестного
входного воздействия по отклику, полученному на выходе системы.
В данном случае нас больше интересует решение обратной задачи.
Формально, для того чтобы решить обратную задачу (восстановить функцию РЛР),
необходимо найти такой оператор, который бы позволил равенство 
превратить в
тождество.
Однако поскольку траекторный сигнал наблюдается всегда в смеси с шумом
, (2)
то задача восстановления функции РЛР по наблюдаемой реализации
может быть решена только приближенно.
Приближенное решение в теории оценивания принято
называть оценкой. Таким образом, РЛИ является оценкой функции РЛР. Поскольку
функция РЛР является комплексной, то и РЛИ оказывается комплексным. Для
практических приложений вместо комплексного используется вещественное РЛИ,
представляющее собой модуль или квадрат модуля комплексного РЛИ.
При статистической формулировке задачи ключевую роль играют уравнения
сообщения и наблюдения [10], а также вид критерия оптимальности. Функция РЛР на
интервале наблюдения (синтезирования) (ИС) не зависит от времени, поэтому
уравнение сообщения выглядит так:
, (3)
Уравнение наблюдения описывается выражением (2), в
котором под шумом наблюдения подразумевается гауссовский случайный процесс,
корреляционная взаимосвязь которого значительно меньше, чем у полезного
(отраженного) сигнала. Поскольку эффективная ширина спектра шума наблюдения
значительно больше полосы пропускания системы обработки, то в пределах этой
полосы его спектральная плотность равномерна, что хорошо согласуется с моделью
комплексного белого шума с нулевым
математическим ожиданием и корреляционной функцией вида
. (4)
Выбор
критерия оптимальности в большинстве случаев основан на интуитивных представлениях
о целевом назначении получаемой оценки. С единых позиций наиболее полно
разработан байесовский подход к вопросам выбора тех или иных критериев
оптимальности оценки, основанный на различных вариациях обобщенного критерия
минимума среднего риска. Обоснованности байесовского подхода способствует то,
что при несущественных для практики ограничениях байесовские правила решения
образуют полный класс [10]. Это означает, что не существует оптимальных правил
статистических решений, которые бы нельзя было получить, используя байесовский
подход. Свобода выбора критерия сводится к произвольному (целесообразному с
интуитивных позиций) выбору функции потерь.
Наиболее
универсальной и часто применяемой на практике мерой близости двух точек
(функции потерь) является квадратичная мера:
. (5)
По своей
физической сущности критерий, использующий различие полей 
и 
в виде выражения (5),
означает, что расстояние между двумя функциями в функциональном пространстве
будет тем больше, чем больше энергия их разности 
. Из теории случайных функций известно, что при одинаковой
энергии на конечном интервале наблюдения наименьшую вероятность из всех
случайных процессов имеет белый шум. Другими словами, критерий, использующий меру
(5), менее всего чувствителен к искажениям 
в виде белого шума.
Это способствует получению более зашумленных, но в то же время более четких (с резкими границами) изображений, чем при использовании других критериев, в которых РЛИ более «сглажены». Поскольку более четкие границы объектов способствуют лучшему их разрешению, то вполне оправдано применение критерия с квадратичной мерой в качестве основного критерия синтеза системы формирования двумерных изображений групповых аэродинамических объектов.
С точки
зрения математической статистики задача синтеза формулируется следующим образом.
Располагая
априорными сведениями о статистических характеристиках функции РЛР и шума
наблюдения, а также известной функциональной зависимостью между функцией РЛР и
наблюдаемой реализацией случайного процесса, требуется найти решающее правило
(алгоритм), позволяющее, используя полученную на ИС реализацию случайного
процесса 
, формировать оценку функции РЛР, оптимальную по байесовскому
критерию с квадратичной функцией потерь.
Общее
решение сформулированной задачи известно [10] и сводится к нахождению оценки,
при которой апостериорная дисперсия имеет наименьшее значение. В формульном
выражении решающее правило выглядит так:
.
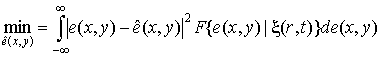(6)
где 
– функционал апостериорной плотности вероятности
функции РЛР 
.
Байесовскую
оценку при квадратичной функции потерь в теории решений называют оценкой,
оптимальной по минимуму СКО, или МСК-оценкой.
Выражение
(6) легко преобразуется к виду
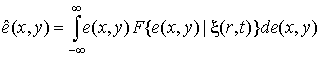, (7)
откуда
следует, что оптимальная по минимуму СКО оценка является апостериорным математическим
ожиданием поля оцениваемых параметров (средним значением апостериорной
плотности вероятности (АПВ)).
Апостериорная
плотность вероятности находится как произведение априорной плотности
вероятности и функции правдоподобия:
, (8)
и
если она симметрична относительно оцениваемых параметров поля 
(например, имеет вид
гауссовского распределения), то ее среднее значение совпадает с максимумом. В
этом случае МСК-оценка оказывается также оптимальной по критерию максимума
апостериорной вероятности (МАВ), т. е.
(9)
и ее вместо выражений (6) или (7) удобнее находить
как решение уравнения:
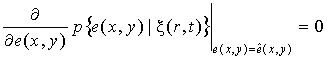. (10)
Для гауссовских распределений математические преобразования будут значительно компактнее, если вместо выражений (9), (10) использовать:
, (11)
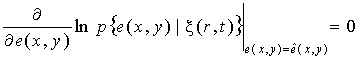. (12)
Как известно из теории статистических решений [11],
в общем случае МАВ-оценка получается как оптимальная байесовская оценка при
простой функции потерь в вид дельта-функции. По сути, это ступенчатая мера различия двух векторов, которая равна
нулю только при абсолютном совпадении всех их компонентов. При малом отличии
хотя бы одного из них она равна бесконечности. Понятно, что этот критерий
различия хорош для задач обнаружения точечных объектов, когда требуется
зафиксировать превышение величины одного из элементарных отражателей модели
функции РЛР над общим фоном. Таким образом, благодаря совпадению МСК- и
МАВ-оценок при гипотезе о гауссовском апостериорном распределении, критерий МСК
также хорошо согласуется с задачей обнаружения целей.
Формула (9)
позволяет разделить в уравнении оценки роли наблюдения и априорных данных:
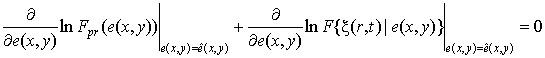. (13)
При слабых
априорных данных:
,
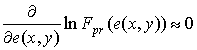оценка, полученная из решения уравнения (13), близка
к оценке по максимуму функции правдоподобия (МП)
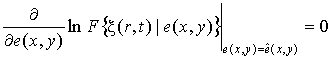. (14)
В теории решений МП-оценка широко используется в тех случаях, когда нет сведений об априорном распределении вероятностей и нельзя отдать предпочтение той или иной функции потерь.
В явном виде аналитические выражения для оптимальных оценок можно получить, если воспользоваться для решения уравнений основными принципами и положениями вариационного исчисления.
Рассмотрим
синтез алгоритма формирования РЛИ, используя общее правилом (9) получения
оценки оптимальной по критериям МСК и МАВ.
Для учета
особенностей наблюдения аэродинамических объектов, воспользуемся более
подробной моделью траекторного сигнала [8]:
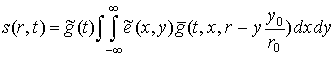, (15)
где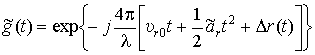 
; 
;
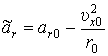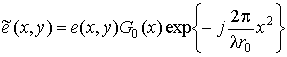(16)
– преобразованная функция
РЛР;
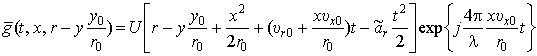. (17)
Если в
качестве информационного параметра использовать функцию 
, то алгоритм будет содержать меньше нелинейных преобразований,
а следовательно, быть более устойчивым.
В качестве
модели непрерывной по пространственным координатам и неизменяющейся во времени
функции РЛР 
будем использовать модель
в виде нестационарного белого гауссовского шума с корреляционной функцией [8]:
и нулевым математическим ожиданием.
Для
преобразованной функции РЛР 
с учетом выражения
(16) корреляционная функция рассчитывается по формуле
. (18)
Как
известно [11], функционал плотности вероятности случайного процесса имеет вид
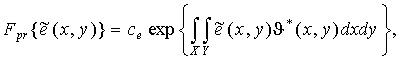(19)
где функция 
находится из
интегрального уравнения
,
которое для корреляционной функции (18) имеет решение:
.
Подставив
это выражение в формулу (19), получим следующее выражение для функционала
априорной вероятности:
,
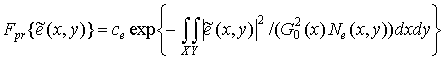где X, Y – область существования функции 
, которая в рассматриваемой задаче зависит от размеров зоны
обзора; 
– нормирующий коэффициент.
В случае
белого гауссовского шума наблюдения функционал правдоподобия
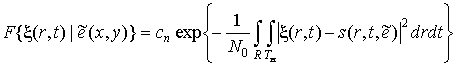
также имеет вид экспоненциальной зависимости и поэтому вместо функционала АПВ (9) удобнее максимизировать его логарифм:
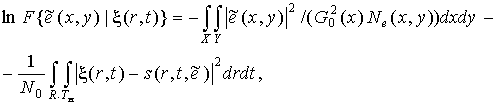(20)
где 
и 
– размеры РГ по
соответствующим координатам.
Из теории
вариационного исчисления известно, что необходимым условием экстремума
функционала является равенство нулю его первой вариации, а функция 
, при которой оно достигается, находится как решение
уравнения Эйлера – Лагранжа. Поскольку интегральные преобразования
обладают свойством линейности, то вместо функционала (20) исследовать на
экстремум можно его подынтегральное выражение
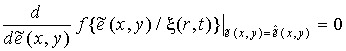, (21)
где 
– подынтегральное
выражение функционала (20), а дифференцирование по функции 
выполняется так же,
как по параметру. Для получения 
из выражения (20) необходимо
подставить выражение для 
, раскрыть квадрат модуля во втором слагаемом и поменять, где
это необходимо, порядок интегрирования.
Подставив в
выражение (21) выражения (15), (20) и выполнив необходимые преобразования,
получим
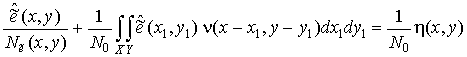, (22)
где 
– оцениваемая
функция, описываемая выражением (16);
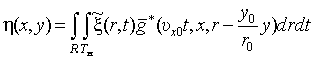
– функция, представляющая собой сигнал на выходе устройства двумерной согласованной обработки;
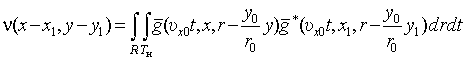
– функция, описывающая отклик
устройства на сигнал от точечной цели (автокорреляционная функция системы
формирования траекторного сигнала); 
– демодулированный
траекторный сигнал.
Выражение
(22) имеет вид неоднородного уравнения Фредгольма второго рода. В случае
однородной модели поверхности, т. е. когда 
интегральное уравнение
(22) сводится к линейному уравнению. Если область интегрирования (X, Y) допускает замену конечных пределов интегрирования на бесконечные, то
решить уравнение (22) можно методом преобразования Фурье, т. е. в
частотной области. Условие замены пределов интегрирования выполняется только в
случае однородной функции РЛР.
Однако из
выражения (18) следует, что даже при модели функции РЛР 
в виде однородного
дельта-коррелированного поля с постоянной спектральной плотностью 
и корреляционной
функцией
функция
будет неоднородной
из-за умножения исходного поля РЛР 
на 
. В результате 
и, следовательно, в
общем виде решить уравнение (22) в частотной области не удается. Но поскольку в
режиме сопровождения групповая цель находится в центре реальной диаграммы
направленности антенны РЛС, то допустимо считать 
, а для однородной модели зоны наблюдения 
.
Выбор
однородной модели в случае наблюдения за аэродинамическими объектами в полете
может вызвать недоумение. И только сравнение статистических характеристик сигналов,
отраженных от однородной поверхности и аэродинамических объектов сложной формы
с отсутствием на них отдельных явно выраженных блестящих точек, позволяет согласиться
с использованием этой модели. Хотя более корректным будет использование неоднородной
модели.
В случае
однородной модели для решения уравнения (22) можно воспользоваться частотным
методом, т. е. методом двумерного преобразования Фурье:
.
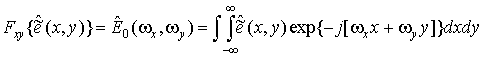Предполагая корректной замену конечных пределов интегрирования бесконечными и применив к обеим частям уравнения (22) преобразование Фурье, получим
,
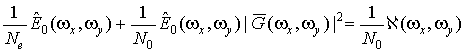откуда
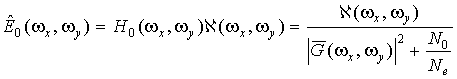, (23)
где 
– Фурье-образ оценки;
– двумерное
Фурье-преобразование сигнала на выходе устройства согласованной обработки; 
; 
– комплексная
частотная характеристика (КЧХ) устройства восстановления (квазиобратного
фильтра), которое формирует оценку функции РЛР, оптимальную по критерию
минимума среднего квадрата ошибки.
Полученное
выражение (23) является двумерным аналогом оптимального стационарного фильтра
Винера [12].
Искомая
оценка 
находится как обратное преобразование Фурье
от оценки, найденной в частотной области:
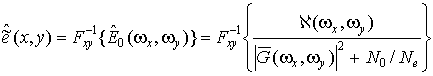, (24)
где
– обозначает двумерное обратное преобразование Фурье.
Для
сравнения найдем оценку функции 
по критерию максимума функционала
правдоподобия (14). В этом случае исследовать на экстремум необходимо логарифм
функционала правдоподобия следующего вида:
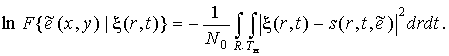
Выполнив
необходимые преобразования, можно получить выражение аналогичное выражению
(22):
. (25)
Решение уравнения
(25) в частотной области имеет вид
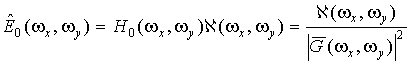. (26)
Решение
(26) отличается от решения (23) только структурой восстанавливающего фильтра.
Восстанавливающий фильтр, используемый в выражении (26), называется обратным.
Необходимость восстанавливающих фильтров и их отличие, с точки зрения физики
протекающих процессов, можно объяснить так.
Пространственный
спектр 
функции РЛР 
подвержен амплитудным
искажениям как в процессе формирования траекторного сигнала, так и в процессе
согласованной обработки. Эти искажения пропорциональны квадрату модуля КЧХ системы формирования
траекторного сигнала 
. Для их устранения и нужен восстанавливающий фильтр.
На первый
взгляд, восстановление амплитуд подавленных гармоник спектра оцениваемого
сигнала 
будет лучше при
использовании алгоритма (26), чем алгоритма (23). Однако поскольку КЧХ реальной
системы формирования траекторного сигнала обычно узкополосная и расположена в
диапазоне низких частот, то фильтр 
, обладая большим коэффициентом усиления на высоких частотах,
очень сильно усиливает высокочастотные составляющие шума наблюдения, что отрицательно
сказывается на устойчивости и качестве функционирования системы обработки.
Фильтр с
КЧХ вида
обеспечивает
необходимое ограничение усиления на уровне, не превышающем отношение
спектральных плотностей восстанавливаемого сигнала и шума наблюдения 
, чем и достигается его устойчивость к шумам.
Используемое
для решения уравнения (23) двумерное преобразование Фурье не всегда выполнимо
или не приводит к желаемым результатам. Это связано с особенностями ядер
интегрального преобразования, а именно с их инвариантностью относительно
разности пар аргументов: r и y, x и t. В частности, при сопровождении групповой
цели ядро интегрального преобразования в операторе L{…} описывается выражением (17). Если в уравнении
(22) используется демодулированный сигнал 
, то в качестве импульсной характеристики в этом уравнении
можно применить упрощенное ядро следующего вида:
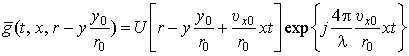. (27)
Для РЛС с
низкой разрешающей способностью по дальности ядро (27) можно еще упростить:
.
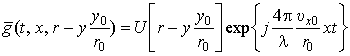Полученное
ядро состоит из двух множителей, каждый из которых зависит только от одной из
пар независимых аргументов. Первый множитель инвариантен относительно разности
аргументов r и
y и описывает ядро преобразования типа свертки.
Второй не имеет инвариантной разности, поскольку аргументы x и t в нем перемножаются, а само ядро эквивалентно
ядру преобразования Фурье. Поскольку преобразование Фурье является одной из
классических операций спектрального (гармонического) анализа входного сигнала,
то алгоритм, основанный на интегральном преобразовании с таким ядром, можно
назвать алгоритмом, использующим способ гармонического анализа [9].
Найдем
решение уравнения (22) с учетом особенностей способа гармонического анализа. По
ядру (27) видно, что применение двумерного преобразования Фурье к уравнению
(22) не приведет к его упрощению, поскольку второй множитель ядра не позволяет
рассматривать второй член уравнения (22) как двумерную свертку. Поэтому
ограничимся преобразованием в частотную область обеих частей уравнения (22)
только по координате наклонной дальности. Тогда, допуская корректной замену конечных
пределов интегрирования по x на
бесконечные, для однородной модели функции РЛР имеем
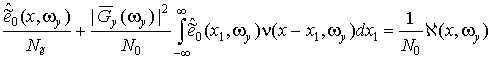, (28)
где
; 
; 
;
.
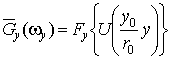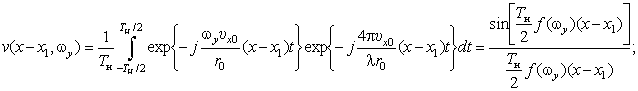
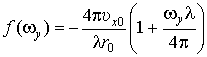В
приближении гармонического анализа траекторный сигнал можно рассматривать как
преобразование Фурье от функции РЛР 
по координате
поперечной дальности 
. Поэтому конечная длина интервала наблюдения 
в рассматриваемой задаче задает ширину
спектра пространственных частот 
искомой функции РЛР.
С учетом этого для вычисления интеграла свертки в левой части (28) можно
воспользоваться фильтрующим свойством функции 
[13]. Для того, чтобы
это свойство строго выполнялось для всех значений пространственной частоты 
, можно ввести новую переменную 
. Тогда
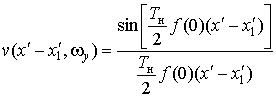
и уравнение (28) примет вид
,
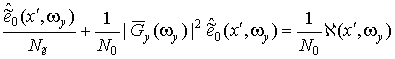откуда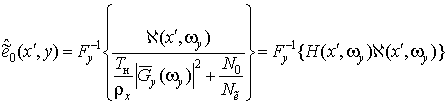 
, (29)
,
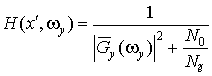где 
.
Понятно,
что полученную таким образом оценку 
можно считать близкой
к оптимальной по критерию МСК, только в области пространственной переменной 
, в которой функция 
. На практике для дальнейшего использования обычно берут оценку
функции РЛР участка поверхности, попадающего в ДН антенны РЛС по уровню не менее
0,707.
Анализируя выражения (23, 26, 29), можно прийти к выводу, что первым
этапом обработки зарегистрированной РГ является согласованная с импульсной
характеристикой системы формирования траекторного сигнала обработка, а вторым –
устранение искажений (восстановление), вызванных условиями формирования и
обработки РГ.
Исследования
МСК-алгоритмов доказали [9], что в отличие от традиционных согласованных
алгоритмов качество (детальность) РЛИ, формируемых с их помощью, зависит от
отношения сигнал-шум (q) на входе. Это подтверждает выражение [9]:
,
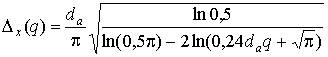где q – отношение сигнал-шум; 
– размер апертуры
антенны.
Найденная
при тех же условиях ширина отклика согласованного фильтра рассчитывается
по выражению: 
.
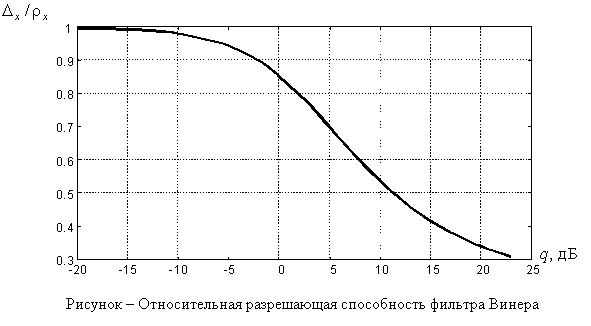
Для сравнения разрешающей способности согласованного и МСК-алгоритмов
целесообразно воспользоваться графиком (рисунок), из которого следует, что уже
при реально существующих в РЛС величинах q = 3 – 5 дБ разрешающая способность
на 20 – 30 % лучше, чем у
согласованного. Улучшение разрешения в 2 раза наблюдается при q = 12 – 15 дБ.
Литература
1. Радиовидение. Радиолокационные системы дистанционного
зондирования Земли / Под ред. Г. С. Кондратенкова. М., Радиотехника,
2005.
2. Лещенко С. П., Горшков С. А., Ширман Я. Д.
Принцип получения двумерных изображений при недостаточном
азимутальном разрешении // Радиотехника и электроника. 1991. Т. 36.
№ 8.
3. Лихачев В. П., Пасмуров А. Я.
Формирование радиолокационных изображений летательных аппаратов при условии частичной
когерентности сигнала // Радиотехника и электроника. 1999.
Т. 44. № 3.
4. Манукьян А. А.
Определение координат локальных неоднородностей на поверхности объекта по
многочастотной амплитудно-фазовой диаграмме обратного рассеяния при наличии
фазовых искажений // Радиотехника и электроника. 1994. Т. 39.
№ 1.
5. Митрофанов Д. Г.
Алгоритмы адаптивного метода построения двумерного радиолокационного изображения // Измерительная
техника. 2004. № 11.
6. Стайнберг Б. Д.
Формирование радиолокационного изображения самолета в диапазоне
СВЧ // ТИИЭР. 1988. Т. 76. № 12.
7. Фархат
Н. Х. Формирование радиолокационных изображений методом разнесения в
диапазоне СВЧ и автоматизированная идентификация целей, основанная на
использовании моделей нейронных сетей // ТИИЭР. 1989. Т. 77. № 5.
8. Вашкевич С. А.
Оптимально-адаптивное формирование радиолокационных изображений в РЛС с
цифровым инверсным синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА
ВПВО ВС РФ, 2007.
9. Карпов О. А.,
Вашкевич С. А. Оптимальная адаптивная обработка сиг-налов в РЛС с
цифровым синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА ВПВО ВС РФ, 2005.
10. Тихонов
В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических
устройств и систем. М., Радио и связь, 1991.
11. Тихонов
В. И. Статистическая радиотехника. М., Радио и связь, 1982.
12. Муш Б. С.,
Кузнецова Ю. В. Практическое использование оператора оптимальной
фильтрации Винера-Колмогорова в квазиголографических системах // Радиотехника.
1983. № 6.
13. Корн
Г., Корн Т. Справочник по математике для научных работников и инженеров.
М., Наука, 1984.
Optimum by
criterion of a
minimum MSE
algorithms of shaping of
the radar-tracking images
of group aerodynamic plants
Vashkevich S. A.
In paper the algorithms of shaping of the radar-tracking images of
group aerodynamic plants are developed optimum by criterion MSE. In a basis of synthesis of these algorithms the theory of
a statistical estimation lays.
Кафедра радиоэлектроники
Военная академия войсковой ПВО ВС РФ
Поступила в редакцию 3.02.2008.