- Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 7. -
Вып. 1. - 2008. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-17-html/TITL-17.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-17-html/cont.htm
УДК
621.396.969
теоретические положения
синтеза
адаптивных оптимальных
и субоптимальных алгоритмов
формирования радиолокационных
изображений групповых аэродинамических объектов
Ó
2008 г. С. А. Вашкевич
В статье на основе
адаптивного байесовского подхода изложены теоретические положения синтеза
адаптивных оптимальных и субоптимальных алгоритмов формирования
радиолокационных изображений групповых сосредоточенных аэродинамических объектов.
Ключевые слова:
радиолокационное изображение; адаптивный байесовский подход; адаптивный
оптимальный (субоптимальный) алгоритм.
Синтезированные в [1] алгоритмы формирования радиолокационных изображений (РЛИ) групповых аэродинамических объектов (ГАО) предусматривают наличие полной априорной информации о статистических характеристиках как наблюдаемого сигнала, так и функции радиолокационного рассеяния (РЛР) группового объекта. Кроме того, при синтезе этих алгоритмов предполагалось, что импульсная характеристика радиоканала «РЛС – среда распространения – наблюдаемый объект» является детерминированной функцией, а ее параметры известны и не изменяются на всем интервале синтезирования (ИС). Однако эти условия практически невыполнимы при инверсном синтезировании апертуры антенны. Обычно статистические характеристики наблюдаемого сигнала, отражающей способности объекта и параметров его движения заранее неизвестны. А траекторные нестабильности полета отдельных объектов и независимость их пилотирования приводят к отличию параметров импульсных характеристик, описывающих движение всей группы и каждого объекта в отдельности.
Известно [2], что статистические алгоритмы в силу относительной нечувствительности к виду статистических распределений параметров входных сигналов могут до некоторого уровня априорной неопределенности сохранять свои качественные характеристики. Традиционные алгоритмы инверсного синтезирования, использующие когерентное накопление, сохраняют качественные характеристики в пределах интервала когерентности отраженного сигнала. Для разных групповых целей и параметров их движения величина этого интервала изменяется в диапазоне от десятков миллисекунд до единиц секунд. От продолжительности ИС зависит угловая разрешающая способность РЛС с инверсным синтезированием апертуры (РИСА). Выбирая ИС (в целях достижения высокой разрешающей способности) больше интервала когерентности, можно столкнуться с ухудшением качества получаемых РЛИ. Причиной этого является незнание свойств отраженного сигнала, а наиболее часто – параметров импульсной характеристики. Априорную неопределенность можно существенно уменьшить, если удастся измерить параметры движения групповой цели с необходимой точностью, а затем использовать их для настройки алгоритмов синтезирования. Но погрешность существующих радиолокационных измерителей (например, радиальной скорости и дальности) существенно превышает допустимый для процесса инверсного синтезирования апертуры антенны диапазон.
В связи с этим задача разрешения ГАО, а с ней и задача инверсного синтезирования апертуры антенны должны ставиться и решаться в условиях существенной априорной неопределенности, когда статистические характеристики входного сигнала и параметры импульсной характеристики заданы приближенно.
Для решения задач статистического оценивания в условиях априорной неопределенности достаточно полно проработан известный математический аппарат адаптивного байесовского подхода, предложенный Р. Л. Стратоновичем [3]. Его отличие от классического неадаптивного варианта [1] заключается, прежде всего, в увеличении числа оцениваемых функций и параметров, а также в использовании эмпирических оценок априорных распределений. Полученные с помощью этого подхода алгоритмы называются адаптивными к изменениям того или иного информационного или сопутствующего параметра.
Цель настоящей статьи заключается в теоретическом обосновании синтеза адаптивных оптимальных и субоптимальных алгоритмов формирования РЛИ ГАО на основе статистической теории оптимального оценивания, а в частности, адаптивного байесовского подхода.
Существующую в
статистическом описании сигнала, отраженного от ГАО, [4] неопределенность можно
свести к параметрическому типу, т. е. описать конечным числом неизвестных параметров 
. В их качестве следует понимать не только неизвестные
числовые значения различных коэффициентов, но и неизвестные функции, вводимые в
модели сигналов и сообщений для раскрытия неопределенности. Это возможно благодаря
тому, что задача статистического синтеза формализуется и решается в рамках аппарата
функционального анализа, где любая функция может рассматриваться как параметр.
Как только
неопределенность удалось свести к конечному числу неизвестных параметров и
функций 
, адаптивная задача может быть решена обычными методами
теорий статистических решений или фильтрации. Включив неизвестные параметры в
число оцениваемых, исходная статистическая задача сводится к оценке
расширенного вектора сообщений 
.
В теории адаптации [3]
изложенный подход называют адаптивным байесовским. Параметры расширенного
вектора сообщений, которые изначально в неадаптивном варианте задачи входили в
число оцениваемых, считают информационными, вновь введенные для раскрытия неопределенности
параметры – сопутствующими. В нашем случае информационным параметром может быть
комплексная функция РЛР 
или вектор
параметров 
, описываемые соответствующими математическими моделями [4].
Все остальные функции и параметры 
, включенные в вектор оцениваемых, являются сопутствующими.
Используя адаптивный
байесовский подход, сформулируем задачу синтеза адаптивных алгоритмов для
получения РЛИ групповой цели. Будем считать, что в функции фазовых искажений
входного сигнала имеется конечное число неизвестных параметров 
, т. е.
неопределенность относится к разряду параметрических.
В процессе наблюдения (
) за групповой целью, движущейся по произвольной траектории,
формируется траекторный сигнал, который в общем случае может быть описан выражением
[4]
, (1)
где 
– расширенный вектор
сообщений; 
– белый комплексный
гауссовский шум с корреляционной функцией
и
функционалом плотности вероятности
.
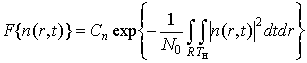В дискретных по
наклонной дальности моделях функции РЛР [4] при отсутствии миграций сигнала
наблюдения в каждом 
-м канале наклонной дальности можно считать независимыми.
Тогда
, (2)
,
.
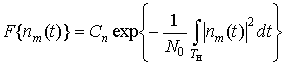Индекс
в дальнейшем будем
опускать.
Для дискретных по обеим координатам
моделей функции РЛР или в других случаях векторного наблюдения [4] имеем
, (3)
,
.
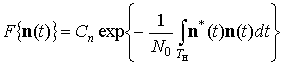Основой адаптивного
байесовского подхода к синтезу информационных систем служит оценка 
, оптимальная по критерию максимума апостериорной вероятности
(МАВ) и полученная для всего расширенного вектора сообщений, а не только для
информационных параметров. Если компоненты вектора сообщений представлены
полями (
) или функциями (
), то алгоритм получения МАВ-оценки имеет вид
(4)
или
(5)
где
, 
– функционалы
апостериорной плотности вероятности.
Если расширенный
оцениваемый вектор содержит набор постоянных на ИС параметров (
= const), то
, (6)
где
– функция
апостериорной плотности вероятности.
Согласно формуле Байеса,
функции и функционалы апостериорной плотности вероятности формируются из
соответствующих априорных характеристик 
, 
, 
и функционалов
правдоподобия 
, 
, 
,
которые получают из функционалов шума наблюдения простой заменой переменных.
Выражения для этих функционалов имеют
вид [2]
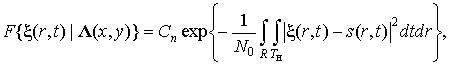(7)
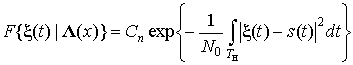, (8)
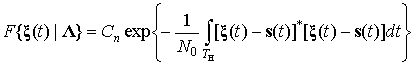. (3.9)
Для симметричных
апостериорных плотностей вероятности (например, гауссовских) МАВ-оценки
оптимальны и по критерию минимума среднего квадрата ошибки (МСК). В случае,
когда априорные плотности вероятности в выражениях (4) – (6) неизвестны,
оценку расширенного вектора сообщений можно искать по критерию максимума
функции правдоподобия (МП):
, (10)
, (11)
. (12)
Эффективным аппаратом
решения задач, в котором может быть использован адаптивный байесовский подход,
является аппарат марковской теории фильтрации. В марковской теории [5]
оперируют моделями, описанными с помощью дифференциальных или разностных
уравнений. Динамические модели функции РЛР [4] полностью соответствуют требованиям,
предъявляемым к моделям в теории фильтрации марковских процессов. Если
аналогичным образом описать сопутствующие параметры, то необходимые для синтеза
уравнения наблюдения и сообщения примут вид
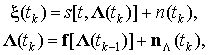(13)
где 
– функция,
связывающая компоненты вектора сообщения на 
и 
шагах; 
– вектор формирующих
шумов.
Основой синтеза
оптимальных алгоритмов, как и ранее, остается критерий МАВ. Но в отличие от
общей теории статистических решений, где оценки формируются по всему массиву
данных, полученных на интервале наблюдения, в теории фильтрации марковских
процессов [2, 5] оценивание выполняется в текущем времени (аналоговая
фильтрация) или в его дискретные моменты (дискретная, или непрерывно-дискретная
фильтрация). Оптимальный по критерию МАВ алгоритм (для случая непрерывно-дискретной
фильтрации) имеет вид
, (14)
где
– массив данных
наблюдаемого на интервале 
траекторного сигнала.
При гауссовском
характере всех распределений байесовские оценки по критерию МАВ будут
оптимальными и по критерию МСК. Для МСК справедливо следующее выражение:
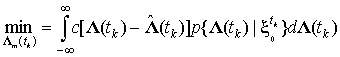(15)
или,
что одно и то же,
.
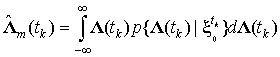(16)
Особенностью оптимальных
алгоритмов, полученных с использованием теории фильтрации марковских процессов,
является то, что они представляют собой набор рекуррентных разностных, или
дифференциальных уравнений.
Отметим, что, включив
вектор параметров неопределенности 
в состав оцениваемого
вектора 
в соответствии с адаптивным
байесовским подходом, в общей структуре синтезируемых алгоритмов можно условно
выделить два параллельных, но взаимосвязанных канала обработки [6]: канал оценки
вектора информационных параметров е
(канал формирования изображения – КФИ) и канал оценки параметров неопределенности
(КОПН) (рис. 1).
Взаимная связь между
каналами проявляется в том, что при оценивании соответствующих информационных
или сопутствующих параметров используются значения смежных оценок, т. е.
при нахождении оценки вектора информационных параметров 
используются оценки
вектора сопутствующих параметров 
и наоборот. В адаптивных
алгоритмах как информационные, так и сопутствующие параметры оцениваются по
одной и той же выборке (реализации) наблюдаемого траекторного сигнала 
. Оценки вектора сопутствующих параметров могут использоваться
как дополнительная информация о решаемой радиолокационной задаче. В случае
разрешения сопровождаемой групповой цели в качестве сопутствующих параметров
используются радиальная скорость и ускорение групповой цели, ее тангенциальная
скорость и т. д. В существующих РЛС радиальное ускорение и тангенциальная
скорость цели могут измеряться только по результатам вторичной обработки. В адаптивных
алгоритмах эти параметры нужны и находятся уже на стадии первичной обработки
отраженного сигнала. Точность их измерений выше, чем при вторичной обработке.
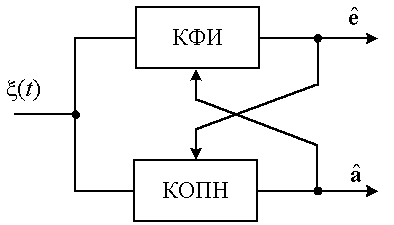
Рис.1.
Обобщенная структура адаптивного байесовского алгоритма формирования РЛИ при параметрической
априорной неопределенности
Однако структура
алгоритмов, синтезированных на основе оптимального байесовского подхода,
получается довольно сложной и не всегда может быть реализована в алгоритмах
первичной обработки сигналов. Поэтому наиболее часто вместо оптимальных алгоритмов
используются суб-оптимальные, которые намного проще своих оптимальных вариантов,
но близки к ним по точности.
Строго формализованных и
единых для всех случаев методов получения простых в реализации субоптимальных
алгоритмов, к сожалению, не существует. Но можно предложить, по крайней мере,
два направления поиска таких алгоритмов. Одно из них основано на разрыве
несущественных связей внутри структуры исходного оптимального адаптивного
алгоритма. Другое заключается в упрощении моделей сигналов, используемых при постановке
задачи синтеза и синтезе адаптивных алгоритмов, оптимальных уже для этих «упрощенных»
моделей. В обоих случаях предполагается, что упрощения как алгоритмов, так и моделей
физически обоснованы, а их корректность проверена, например, с помощью математического
моделирования и желательно по реальным сигналам.
Следуя первому направлению,
разорвем связь между каналом КОПН и вектором оценок 
(рис. 1). Это
допустимо, если оценки 
и 
независимы.
Действительно, поскольку их спектральные характеристики существенно различаются,
то эти оценки можно считать независимыми. Энергетический спектр фазовых
параметров, обычно используемых в качестве параметров неопределенности, лежит в
низкочастотной области, а его полоса не превышает десятка герц. Положение же
максимума энергетического спектра функции РЛР зависит от тангенциальной
составляющей скорости движения групповой цели и при тех условиях, когда
возможно инверсное синтезирование, находится в районе десятков, а то и сотен
герц.
Основное преимущество
новой структуры (рис. 2) заключается в том, что алгоритмы функционирования
в КФИ и КОПН можно синтезировать раздельно и независимо друг от друга.
Например, при синтезе алгоритмов работы КФИ считать параметры фазовых искажений
а известными, что существенно
упрощает синтез. В процессе же функционирования КФИ вместо значений а
использовать их оценки (
), полученные в КОПН. Поэтому в качестве алгоритмов обработки
сигналов в КФИ могут применяться нерекуррентные (синтезированные на основе
теории статистических решений) и рекуррентные (разработанные с помощью теории
фильтрации) оптимальные алгоритмы [1, 6, 7] или их различные субоптимальные
варианты.
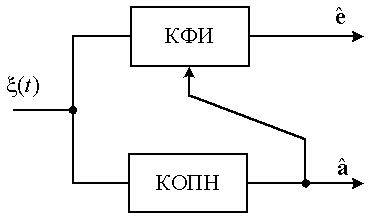
Рис.
2. Структура устройства обработки с независимыми каналами
Кроме того, при независимом
синтезе алгоритмов функционирования КОПН можно существенно уменьшить количество
оцениваемых параметров функции РЛР,
которые в этом случае выступают в роли сопутствующих.
Таким образом, разорвав
несущественную связь в структуре оптимального фильтра (сделав каналы КФИ и КОПН
независимыми), удается упростить как сам синтез, так и разрабатываемые в нем
алгоритмы.
Второе
направление уменьшения вычислительной сложности алгоритмов заключается в том,
что поскольку задача синтеза алгоритма адаптации не связана с необходимостью
получения полноценных оценок функции РЛР, то имеется возможность упростить
модели, описывающие их статистические характеристики, существенно уменьшить их
количество и, кроме того, так сформулировать задачу оценивания, чтобы для ее
решения допустимо было использовать быстрые вычислительные алгоритмы, например
БПФ.
Необходимо отметить, что
адаптивный байесовский подход имеет ряд особенностей, которые затрудняют
процесс оценивания. Сущность основных из них заключается в следующем [3].
1. Каждый из
введенных в число оцениваемых параметров требует априорного статистического
описания, что при существенной неопределенности довольно проблематично.
2. Параметры,
связанные с неопределенностью решаемой задачи, могут входить в уравнения
сообщения и наблюдения нелинейно, что приводит к алгоритмам оценивания в виде
условно незамкнутых систем уравнений.
3. Точность
оценивания снижается пропорционально увеличению размерности вектора оцениваемых
параметров.
Для уменьшения влияния
этих недостатков существует много способов, выбор которых зависит от особенностей
решаемой задачи. Кратко можно пояснить сущность этих способов.
Во-первых, если
неизвестны априорные распределения функций или параметров, то их можно заменить
любым достаточно плавным и удобным для
математических преобразований распределением. Этот принцип основан на
асимптотической нечувствительности оптимальных алгоритмов к априорному
распределению. Неопределенность распределений можно также описать параметрически,
а неизвестные параметры вновь включить в число оцениваемых. Однако следует
помнить, что для всех вновь вводимых параметров и функций также потребуются
априорные распределения. Разомкнуть этот круг можно за счет использования
МП-оценок вновь введенных параметров, которые не нуждаются в априорном описании.
Во-вторых, в рамках
адаптивного байесовского подхода возможна замена априорных распределений или
неизвестных параметров этих распределений их эмпирическими оценками,
полученными по обучающим выборкам. Однако в большинстве реальных ситуаций
получить специальную обучающую выборку в РИСА не представляется возможным.
В-третьих, недостаток
адаптивного байесовского подхода, заключающийся в снижении точности совместных
оценок с увеличением числа оцениваемых параметров и функций, что устраняется
увеличением продолжительности наблюдения или количества независимых каналов
наблюдений. В РИСА – это комплексирование измерений по различным каналам наклонной
дальности (расширение вектора наблюдений).
В-четвертых,
если параметры входят в уравнения сообщения и (или) наблюдения нелинейно, то
могут быть использованы различные методы линеаризации уравнений относительно
интересующих параметров. Возможно также применение других методов теории
нелинейной фильтрации, в частности, метода гармонического оценивания в
квазилинейных алгоритмах для расширения области их сходимости.
Таким
образом, оптимально-адаптивные алгоритмы формирования РЛИ ГАО в соответствие с
адаптивным байесовским подходом должны оценивать по критериям МАВ или МСК не
только параметры функции РЛР, но и сопутствующие фазовые параметры отраженного
сигнала. Оптимальные адаптивные алгоритмы сложны и поэтому возникают большие
трудности их реализации в системе первичной обработки радиолокационных сигналов.
Для получения более простых субоптимальных алгоритмов можно разорвать одну из
перекрестных связей, что позволяет существенно упростить синтез адаптивных алгоритмов.
В процессе синтеза следует применять различные методы преодоления негативных
особенностей адаптивного байесовского подхода.
Работа
выполнена в рамках проекта № 07-07-96401 регионального конкурса «Центр»
при финансовой поддержке администрации Смоленской области и РФФИ.
Литература
1. Вашкевич
С. А. Оптимальные по критерию минимума средних квадратов
алгоритмы формирования радиолокационных изображений групповых аэродинамических
объектов // Мат.
морфология: Электронный мат. и медико-биологический журн. 2008. Т. 7. № 1. URL: http://www.smolensk.ru/
user/sgma/ MMORPH/ N-17-html/ vashkevich-2/vashkevich-2.htm
2. Тихонов
В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических
устройств и систем. М., Радио и связь, 1991.
3. Стратонович Р. Л.
Принципы адаптивного приема. М., Сов. радио, 1973.
4. Вашкевич
С. А. Аналитико-статистическое описание сигнала, отраженного от групповой воздушной цели, ориентированное
на разработку оптимальных по критерию минимума СКО алгоритмов формирования радиолокационных
изображений // Мат.
морфология: Электронный мат. и медико-биологический журн. 2008. Т. 7. № 1. URL: http://www.smolensk.ru/user/
sgma/MMORPH/N-17-html/vashkevich/vashkevich.htm
5. Ярлыков
М. С., Миронов М. А. Марковская теория оценивания случайных процессов.
М., Радио и связь, 1993.
6. Карпов О. А.,
Вашкевич С. А. Оптимальная адаптивная обработка сиг-налов в РЛС с
цифровым синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА
ВПВО ВС РФ, 2005.
7. Вашкевич С. А.
Оптимально-адаптивное формирование радиолокационных изображений в РЛС с
цифровым инверсным синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА
ВПВО ВС РФ, 2007.
Theoretical positions of
synthesis of adaptive optimum and suboptimal algorithms
of shaping of
the radar-tracking images of
group aerodynamic plants
Vashkevich S. A.
In paper on the basis of the statistical adaptive
approach the theoretical positions of synthesis of adaptive optimum and suboptimal
algorithms of shaping of the radar-tracking images of the group concentrated
aerodynamic plants are explained.
Кафедра радиоэлектроники
Военная академия войсковой ПВО ВС РФ
Поступила в редакцию 2.04.2008.