- Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 7. -

Вып. 1. - 2008. - URL:

 

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ

 

http://www.smolensk.ru/user/sgma/MMORPH/N-17-html/TITL-17.htm

 

http://www.smolensk.ru/user/sgma/MMORPH/N-17-html/cont.htm

 

 

 

УДК 621.396.969

 

 Аналитико-статистическое  описание  сигнала, отраженного  от  групповой  воздушной  цели,  ориентированное  на  разработку оптимальных  по  критерию  минимума  СКО  алгоритмов  формирования  радиолокационных  изображений

 

Ó 2008 г. Вашкевич С. А.

 

(vashkevich.doc)

 

В статье разрабатываются математические модели радиолокационного сигнала, отраженного от групповой воздушной цели, пригодные для априорного описания процесса наблюдения при синтезе оптимальных по критерию СКО алгоритмов формирования радиолокационных изображений.

Ключевые слова: радиолокационное изображение; модель отраженного сигнала; критерий минимума СКО; оператор радиолокационного зондирования

 

 

Известно [1, 2], что для синтеза оптимальных по критерию минимума средней квадратичной ошибки (СКО) алгоритмов оценивания (фильтрации), которые можно использовать в качестве алгоритмов формирования радиолокационных изображений, необходимо априорное аналитико-статистическое описание свойств оцениваемых параметров и помех на интервале наблюдения. Априорное описание должно быть в виде так называемых уравнений наблюдения и сообщения. В качестве наблюдения при цифровом инверсном синтезировании апертуры антенны используется смесь отраженного радиолокационного (полезного) сигнала и помехи с известными вероятностными характеристиками.

Целью настоящей статьи является разработка математической модели (ММ) сигнала, отраженного от групповой воздушной цели, адекватно описывающую физические процессы взаимодействия электромагнитных волн, объектов наблюдения и окружающей среды на интервале синтезирования, а также удовлетворяющей форме уравнения наблюдения для дальнейшего использования в процессе синтеза оптимальных алгоритмов формирования радиолокационных изображений.

Для описания процессов излучения, распространения, отражения и приема зондирующего сигнала на интервале синтезирования воспользуемся фильтровым подходом к моделированию отраженного (траекторного) сигнала [2, 3]. Особенность этого подхода заключается в том, что перечисленные физические процессы описываются математически в виде отображения множества отражающих элементов цели на множество элементов регистрируемого в РЛС сигнала (радиоголограммы). Поскольку процессы при условии достаточности динамического диапазона приемного тракта принято считать удовлетворяющими свойству линейности, то оператор преобразования также будет линейным. В теории линейных систем в основном используются матричные (дискретные) и интегральные (непрерывные) операторы.

Опишем процесс формирования траекторного сигнала с помощью линейного интегрального оператора (оператора радиолокационного зондирования):

 

,                 (1)

 

где  – функция радиолокационного рассеяния [5];  – ядро интегрального преобразования, соответствующее сигналу на выходе оператора L при воздействии на его вход функции радиолокационного рассеяния (РЛР) в виде единичного дельта-импульса с координатами , т. е. одного элементарного (точечного) отражателя.                            

Отсутствие координаты z в выражении (1) объясняется свойством фильтрового подхода, при котором функция РЛР должна быть определена в плоскости изображения, где используются всего лишь две координаты – x и y. Следует отметить, что разработанные в [6] ММ функции РЛР удовлетворяют этому свойству.

Ядро интегрального оператора имеет смысл импульсной характеристики системы «РЛС – среда распространения» и описывается выражением

 

,         (2)

 

где  – функция, учитывающая модуляцию сигнала ДН антенны РЛС;  – закон изменения комплексной огибающей зондирующего импульса, выраженный в независимой пространственной координате наклонной дальности  ( и  – скорость и время распространения радиоволн);  – закон изменения текущего расстояния РЛС – цель, определяющий задержку комплексной огибающей отраженного сигнала по шкале наклонной дальности;  – закон изменения фазы отраженного сигнала.

Из существующих режимов функционирования наземных РЛС наиболее приемлемым для инверсного синтезирования апертуры антенны является режим сопровождения цели, обеспечивающего длительное когерентное накопление.

В этом режиме центр диаграммы направленности антенны (ДНА) отслеживает угловые перемещения аэродинамических объектов, т. е. положение объектов наблюдения в ДНА на интервале синтезирования не изменяется: . Кроме того, отраженный сигнал стробируется по дальности, что не допускает захвата аэродинамических объектов, находящихся на других дальностях.

Из анализа выражения (2) следует, что импульсная характеристика оператора радиолокационного зондирования зависит от закона изменения текущего расстояния до цели. Выражение, описывающее этот закон для центра сопровождения групповой цели, найдено в монографии [6] и имеет вид

 

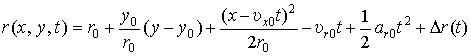,      (3)

 

где ,  – наклонная и горизонтальная дальности центра сопровождения; ,  – радиальная и тангенциальная скорости групповой цели;  – радиальное ускорение цели;  – случайное приращение наклонной дальности, учитывающее флуктуации фазы отраженного сигнала.

В выражении (3) сумма первых двух слагаемых равна дальности до центра сопровождения групповой цели в начале интервала синтезирования. Три следующих слагаемых описывают закон изменения дальности на этом интервале, а последний член учитывает эквивалентное приращение дальности, вызванное фазовыми флуктуациями отраженного сигнала.

Подставив выражения (2) и (3) в формулу (1) и учитывая перенос комплексной огибающей на расстояние , соответствующее задержке отраженного сигнала с точностью до случайной начальной фазы переотражения, получим

 

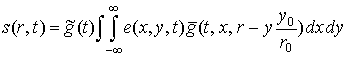,                  (4)

 

где 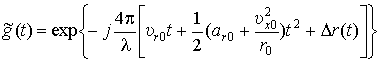 – мультипликативный фазовый множитель, учитывающий радиальное приближение объектов наблюдения и траекторные нестабильности;

 

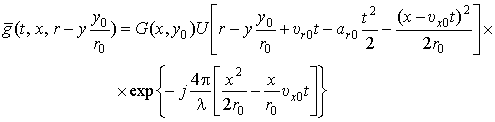          (5)

 

– ядро интегрального преобразования.

По полученным выражениям можно охарактеризовать некоторые особенности отраженного сигнала и этапы последующей его обработки.

Анализ выражения (4) показывает, что мультипликативный фазовый множитель  не зависит от переменных x и y и поэтому вынесен за пределы интегрального оператора, т. е. он влияет не на процесс преобразования функции РЛР  в операторе L, а на его результат. Зависимость этого множителя от времени подчеркивает нестационарность оператора формирования траекторного сигнала. Поэтому первичными этапами обработки радиоголограммы будут этапы, связанные с компенсацией влияния мультипликативного фазового множителя .

Рассмотрим более подробно составляющие  и их влияние на спектральные характеристики траекторного сигнала.

Наличие радиальной скорости , а значит и доплеровской частоты  в мультипликативном фазовом множителе говорит о смещении спектра отраженного сигнала на , которое в процессе обработки потребуется устранить. Поскольку радиальная скорость цели в РЛС измеряется приближенно, то целесообразнее эту операцию выполнить адаптивным методом, используя анализ радиоголограммы.

Присутствующие в  радиальное ускорение и тангенциальная скорость могут привести к расширению спектра отраженного сигнала и ухудшению его когерентных свойств. Эти составляющие вызывают квадратичный набег фазы отраженного сигнала. Поэтому одним из этапов обработки радиоголограммы должна быть компенсация этого набега.

Влияние траекторных нестабильностей () также проявляется через множитель  и приводит как к смещению спектра траекторного сигнала, так и к его расширению. Поэтому компенсирующие алгоритмы должны быть либо инвариантными, либо адаптивными к параметрам траекторных флуктуаций.

Из анализа выражения (5) следует, что положение комплексной огибающей

 

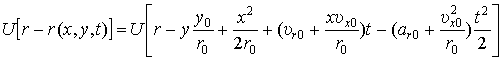     (6)

 

по координате наклонной дальности (r) в течение интервала синтезирования будет изменяться. Этот эффект называется миграцией сигнала по дальности. Если величина миграции сигнала на интервале синтезирования меньше половины элемента разрешения по дальности, то ею можно пренебречь. В формульном представлении это означает следующее:

 

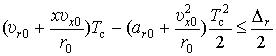,                            (7)

 

где  – величина элемента разрешения по дальности.

Понятно, что условие (7) будет выполняться только для РЛС с инверсным синтезированием апертуры антенны, обладающей низким разрешением по дальности, т. е. элемент разрешения более ста метров. В противном случае в процессе обработки сигнала приходится устранять (компенсировать) его миграцию с помощью адаптивных алгоритмов.

С учетом пренебрежения или устранения миграции, выражение (6) примет вид

 

.

 

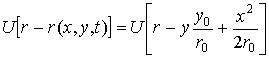В режиме сопровождения цели значение x мало, и поэтому комплексная огибающая будет зависеть только от переменных r и y.

Фазовый множитель ядра интегрального преобразования (5) зависит только от x, что позволяет разделить ядро интегрального преобразования на два независимых множителя:

 

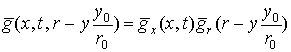,                           (8)

 

а сам оператор L записать в виде

 

.                         (9)

 

Это означает, что процесс формирования траекторного сигнала при инверсном синтезировании можно представить как последовательное применение к функции РЛР двух одномерных линейных операторов Lr и Lx.

Оператор преобразования по наклонной дальности представляет собой линейный интегральный оператор типа свертки

 

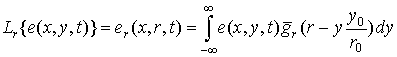.           (10)

 

Оператор преобразования по поперечной дальности эквивалентен интегральному обратному преобразованию Фурье функции РЛР к пространственной частоте ,

 

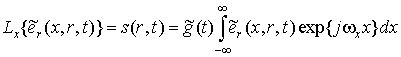,           (11)

 

где 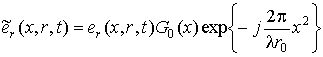   – функция РЛР, умноженная на некоторую комплексную неслучайную функцию. Модуль этой функции зависит от формы ДНА РЛС , а фаза изменяется в зависимости от координаты  по квадратичному закону. Обычно сопровождаемая цель находится вблизи центра диаграммы направленности, т. е. , а . Тогда с точностью до постоянного множителя

 

.

 

Выражения (8) – (11) описывают непрерывную по всем входящим в нее аргументам математическую модель траекторного сигнала. Непрерывная модель компактна при записи и хорошо отражает физику процессов.

Однако при аналитических исследованиях иногда бывает важно сконцентрировать внимание на процессах формирования и обработки сигнала по какой-нибудь одной из пространственных координат. В этом случае потребуется модель, в которой интересующая координата изменяется непрерывно, а все остальные – дискретно.

Кроме того, в РЛС с цифровым инверсным синтезированием апертуры антенны сигналы обрабатываются в дискретной (цифровой) форме как по наклонной дальности , так и по времени наблюдения . Дискретизация по наклонной дальности выполняется в аналогово-цифровом преобразователе на выходе квадратурного фазового детектора или на выходе усилителя промежуточной частоты (при оцифровке сигнала на промежуточной частоте) приемного тракта РЛС, а дискретизация по времени наблюдения возникает вследствие импульсного характера излучения станции.

Например, рассмотрим непрерывную по координате   и дискретную по наклонной дальности  модель отраженного сигнала. Ограничимся простой формой огибающей зондирующего импульса РЛС – прямоугольной или гауссовой формы – без внутриимпульсной частотной или фазовой модуляции. Это ограничение не сказывается на синтезе алгоритмов формирования радиолокационного изображения, но позволяет значительно упростить математические выкладки и сделать более понятным физический смысл полученных выражений.

Из анализа выражения (4) следует, что от переменной r зависит только ядро интегрального преобразования (импульсная характеристика), которое в дискретной форме будет иметь вид вектор-функции

 

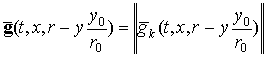         ,                            (12)

 

 

где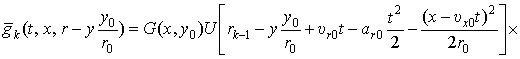     

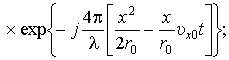
,  – шаг дискретизации сигнала на выходе  АЦП по наклонной дальности,  k = 1, 2, ..., K.

Подставив выражение (12) в выражение (4), получим дискретную по наклонной дальности и непрерывную по времени наблюдения модель траекторного сигнала:

 

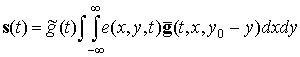                    ,                   (13)

 

где   – вектор-функция сигнала.

Если воспользоваться дискретно-непрерывной моделью функции РЛР [6]

 

,

 

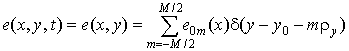где 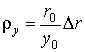,  то выражение (13) примет следующий вид:

 

,

 

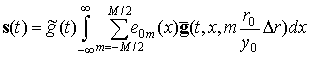где                                  ;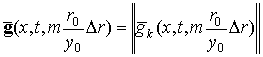

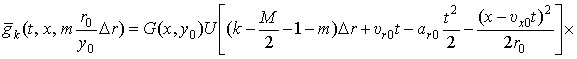
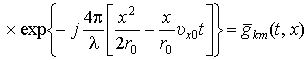.                       (14)

Или более компактно в векторно-матричной форме записи:

 

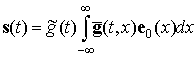                                      ,                             (15)

 

где   – матрица импульсных характеристик;  – вектор-функция параметров РЛР; ;  – количество отсчетов дальности в сигнале, отраженном от наблюдаемых объектов.

При соблюдении условий разделения ядра интегрального преобразования (4) матрица  становится диагональной, что позволяет свести модель (15) к системе M независимых уравнений, различающихся только номером дальностного канала:

 

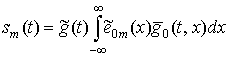                      ,                              (16)

 

где 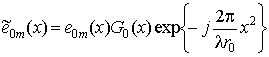 ;  – ядро Фурье-преобразо-вания вида

.

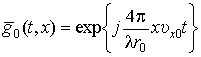Для того чтобы получить дискретную модель по трем координатам r, x, y, необходимо в выражение (16) подставить дискретную по x модель функции РЛР [5, 6]. В результате этого получим

 

,                                     (17)

 

где ; ; .

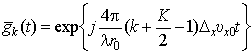Размерность векторов (K) в выражении (17) зависит только от размеров зоны обзора (ширины ДНА РЛС , где da – азимутальный раскрыв антенны РЛС) и величины элемента разрешения по поперечной дальности (). Она не зависит как от длительности интервала наблюдения, так и от выбора момента наблюдения:

 

,

 

т. е. значения компонент вектора  постоянны.

Подводя итоги описанию и анализу ММ траекторного сигнала, отраженного от группы аэродинамических объектов, необходимо отметить:

Во-первых, все полученные ММ эквивалентны и взаимозаменяемы.

Во-вторых, траекторному сигналу свойственны миграции по наклонной дальности на интервале синтезирования, что усложняет как модели сигнала, так и дальнейшую его обработку.

В-третьих, при отсутствии миграций или их компенсации оператор РЛЗ делится на два одномерных оператора: Lr и Lx. Оператор РЛЗ по наклонной дальности (Lr) имеет вид оператора типа свертки, а оператор РЛЗ по поперечной дальности (Lx) описывается обратным преобразованием Фурье.

 

 

Литература

 

1. Сейдж Э. П., Мелс Д. Л. Теория оценивания и ее применение в связи и управлении: Пер. с англ. / Под ред. Б. Р. Левина. М., Связь, 1976.

2. Тихонов В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических устройств и систем. М., Радио и связь, 1991.

3. Афиногенов А. Ю., Школьный Л. А. Методы мат. моделирования радиолокационных изображений искусственных распределенных объектов // Зарубежная радиоэлектроника. 1998. № 2.

4. Школьный Л. А. Два способа описания оператора зондирования при синтезе систем обработки сигналов в РСА по координате путевой дальности // Импульсная техника и дискретная обработка информации: Сб. науч.-метод. материалов. М., Изд-во ВВИА, 1981.

5. Карпов О. А., Вашкевич С. А. Оптимальная адаптивная обработка сигналов в РЛС с цифровым синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА ВПВО ВС РФ, 2005.

6. Вашкевич С. А. Оптимально-адаптивное формирование радиолокационных изображений в РЛС с цифровым инверсным синтезированием апертуры антенны: Монография. Смоленск, Изд-во ВА ВПВО ВС РФ, 2007.

 

 

Analytic-statistical  exposition  of  a  signal reflected  from  a  group  air  target,  oriented  on development  optimum  by  criterion  of  a  minimum  MSE  of shaping’s  algorithms  of  the  radar-tracking  images

 

Vashkevich S. A.

 

In paper the mathematical models of a radar-tracking signal reflected from a group air target, suitable for a priori exposition of process of observation are developed at synthesis optimum by criterion MSE of algorithms of form’s the radar-tracking images.

 

 

Кафедра радиоэлектроники

Военная академия войсковой ПВО ВС РФ

Поступила в редакцию 24.01.2008.