Математическая морфология.
Электронный математический и медико-биологический журнал. - Т. 7. -
Вып. 2. - 2008. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-18-html/TITL-18.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-18-html/cont.htm
УДК 57.001.6
Количественные аспекты злокачественного роста
Ó 2008 г.
Седова Г. П.
(sedova.doc)
Исследование
посвящено изучению количественных аспектов злокачественного роста.
Рассматривается кинетика нарастания массы многоклеточного организма при нормальном
росте, кинетика роста злокачественной опухоли, зависимость снижения потенциала
роста от нарастающей массы. Вводится понятие «короткодействие». Приводится гипотеза
злокачественного роста.
Ключевые
слова: злокачественный
рост, кинетика нарастания массы, кинетика роста, короткодействие.
Содержание
1. Кинетика нарастания массы многоклеточного организма при нормальном росте.
2. Кинетика роста злокачественной опухоли.
3. Зависимость
снижения потенциала роста от нарастающей массы. Короткодействие.
4. Гипотеза злокачественного роста.
1
Кинетика нарастания массы многоклеточного организма при нормальном росте
В основе роста
всего живого лежит удвоение начальной массы. Рост живых организмов происходит
по одному и тому же шаблону, а именно, материнская клетка, достигнув
предельного размера, делится на две, каждая из которых дорастает до размеров
материнской клетки. Т.о., за данный промежуток времени, называемый клеточным
циклом, происходит удвоение массы. Величиной этого цикла и различается рост
различных клеток. Никакая клетка не образуется в
единственном числе из образующих ее элементов.
«Клетка от
клетки» __ таков закон биологии, не знающий исключений. Величина клеточного
цикла показывает как быстро происходит деление клеток, т.е. она характеризует
интенсивность биосинтетических процессов.
В проточной
культуре, когда с постоянной скоростью подается питание и отводится часть
культуральной жидкости, чтобы не накапливались тормозящие рост продукты жизнедеятельности,
биомасса удваивается через один и тот же промежуток времени. Назовем его
периодом удвоения массы. Например, культура кишечной палочки удваивает свою массу
каждые 20 минут.
Математически
рост подобных популяций выражается следующей формулой
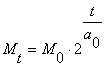 (1)
(1)
где
Mt
- масса в момент
времени t;
Mo - начальная масса;
T - время;
ao - период удвоения массы.
Из этой формулы следует, что период удвоения массы такой популяции равен
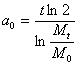
и он будет одним и
тем же, для какого бы момента времени мы его ни вычислили.
Многоклеточный организм в сущности тоже представляет популяцию клеток, но в отличие от проточной культуры эти клетки связаны между собой в единую массу.
Попытаемся распространить формулу (1) на многоклеточный организм. Что в
этом случае в ней изменится?
Как и в случае популяции, рост многоклеточного
организма начинается с начальной массы, а именно, если это эмбриональный рост,
то это масса зиготы, если речь идет о постэмбриональном росте, то это масса
организма в момент рождения. Поэтому Mo в формуле сохранится. Число 2 в
формуле также сохранится, т.к. и в многоклеточном организме рост происходит путем
удвоения массы. Время t __ объективная
реальность, от нас независящая. Изменится только период удвоения массы a. Понятно, что в случае многоклеточного организма он уже не будет
постоянной величиной, а будет какой-то функцией времени. Чтобы определить,
какой именно, обратимся к экспериментальным данным.
Проведем рассуждения в общем виде.
Пусть многоклеточный организм в
в момент времени t1 имеет массу M1,
в момент времени t2 имеет массу M2,
в момент времени t3 имеет массу M3,
и т.д.
Вычислим периоды удвоения массы, соответствующие указанным моментам времени, т.е. ставим вопрос таким образом:
С каким бы
периодом должна была бы удваиваться масса M0, чтобы за время t1 дорасти до массы M1, если бы это удвоение было равномерным?
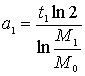 .
.
С каким бы
периодом должна была бы удваиваться масса M0, чтобы за время t2 дорасти до
массы M 2 ,если бы это удвоение было
равномерным?
 .
.
С каким бы
периодом должна была бы удваиваться масса M0., чтобы за время t3 дорасти до массы M 3 , если бы это удвоение было равномерным?
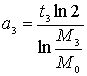 ,
,
и т.д.
Если бы подобные вычисления
были произведены для проточной культуры, то величины a1, a2, a3 и т.д. были бы
равны. Но в случае многоклеточного организма они образуют возрастающую
последовательность, т.к. для удвоения массы многоклеточному организму требуется
все большее количество времени.
По изменению
величин a1, a2, a3 и т.д. мы можем судить о том, по какому
закону замедляется рост многоклеточного организма. Нанесем полученные значения
на график a=f (t).
По горизонтальной
оси отложим время t, обычное время, которое течет независимо от нас, по
вертикальной оси __ время удвоения массы, соответствующее данному моменту времени t.
Назовем его
периодом удвоения массы. Обозначим буквой a .
Когда мы
обратимся к экспериментальным данным по росту различных организмов, вычислим для
каждого из них величины a1, a2, a3 и т.д. и построим график a=f ( t) , то увидим, что он представляет собой прямую линию.
Следовательно, масса многоклеточного организма удваивается с линейно возрастающим периодом.
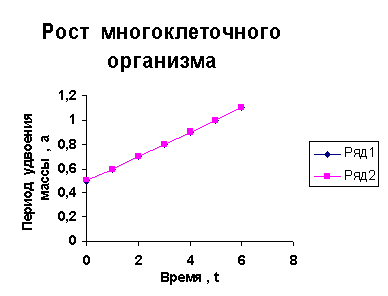
Данная закономерность проверена мною на большом количестве
взятых из литературы экспериментальных
данных. Исключений не обнаружено. Более
подробно вывод указанной закономерности выполнен мною в статье
«Закономерность роста биологических объектов»,
напечатанной в электронном
математическом и медико-биологическом журнале «Математическая
морфология» за 2004 г. [1].
Линейный характер зависимости периода удвоения массы от времени имеет место не только для целых многоклеточных организмов, но и для отдельных органов и тканей, одноклеточных организмов и вообще для всех биологических объектов. Но поскольку мы желаем подойти к злокачественному росту, а он имеет место только в многоклеточных организмах, будем рассматривать только многоклеточные организмы.
Приведем несколько примеров эмбрионального и постэмбрионального роста многоклеточных организмов в качестве иллюстрации указанной закономерности.
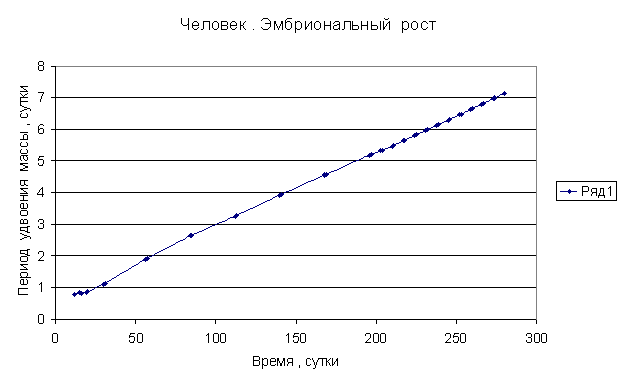

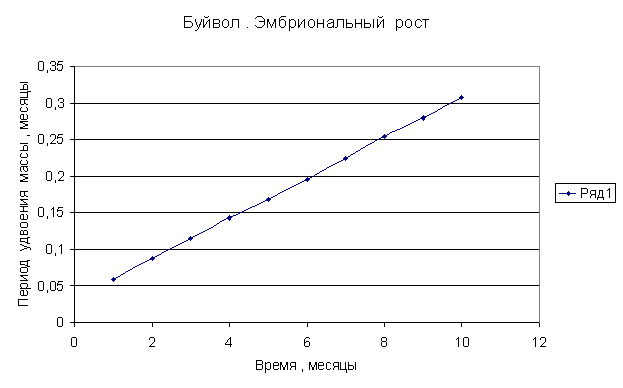



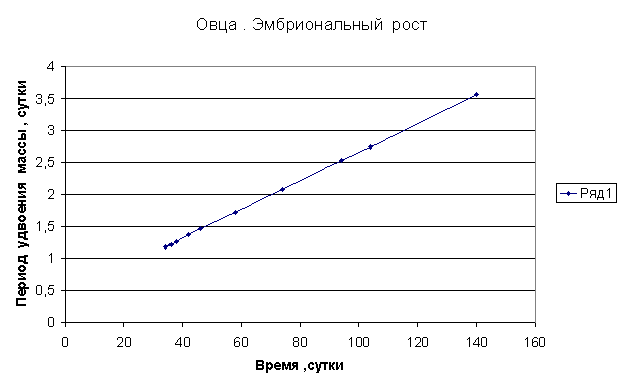

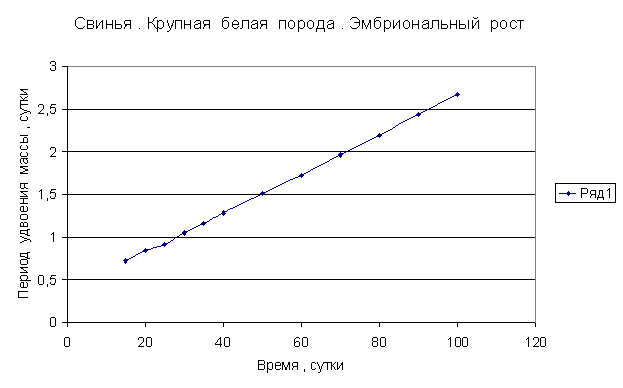
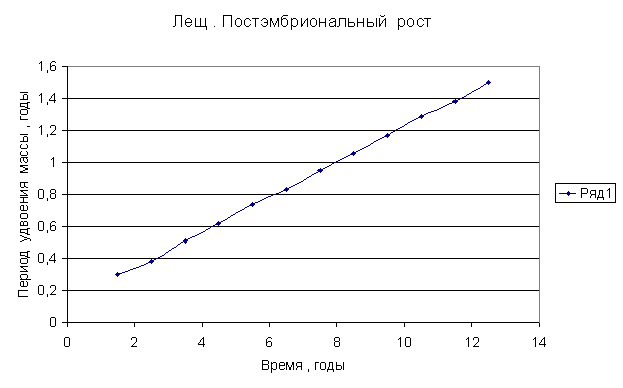

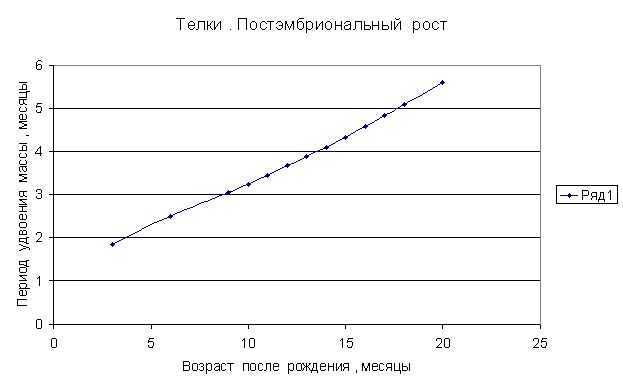

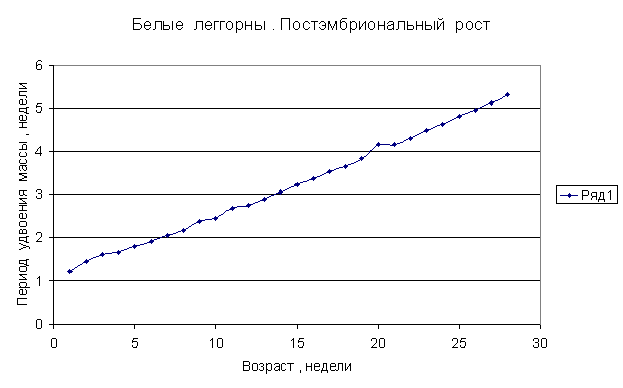

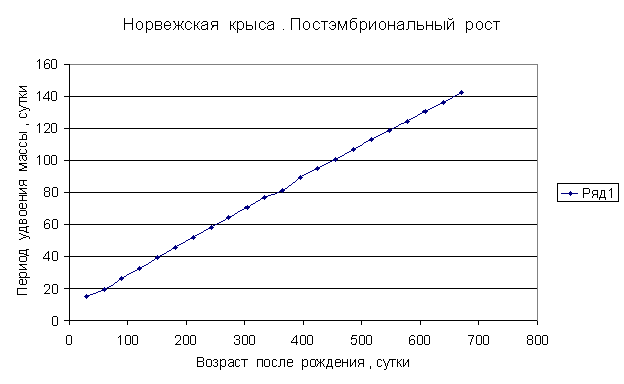

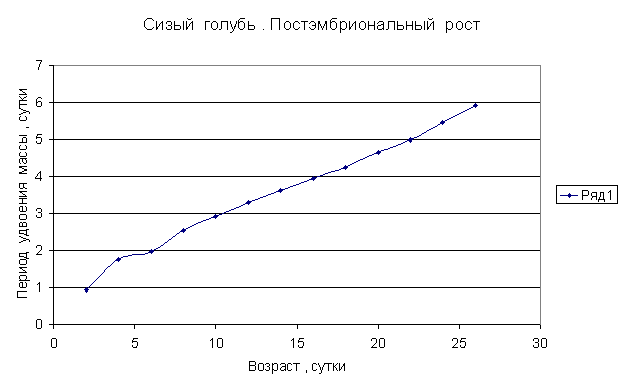
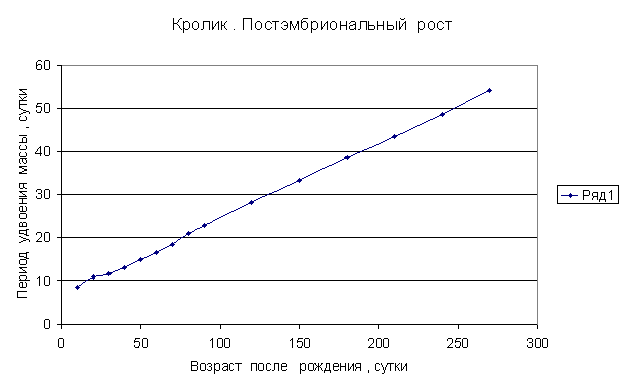

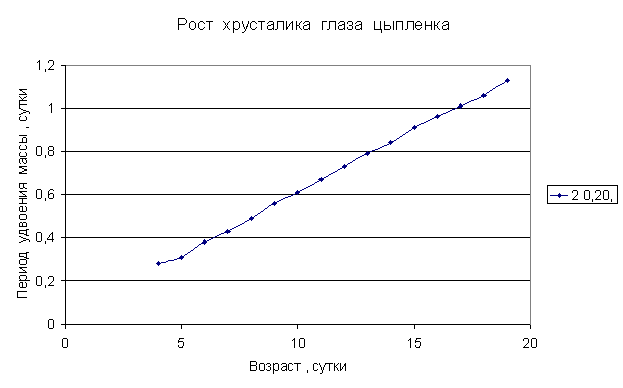

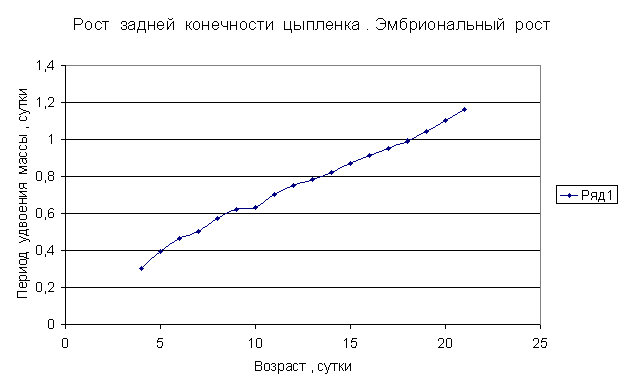

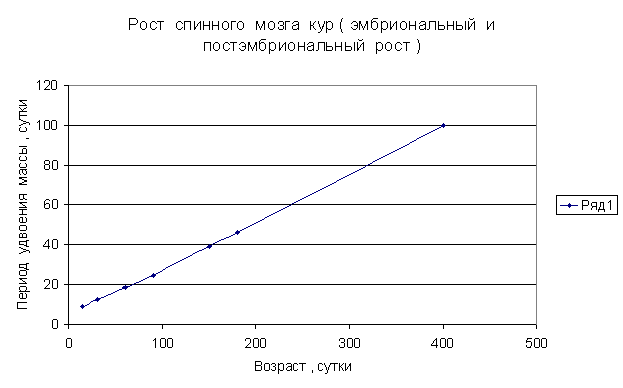
 П
П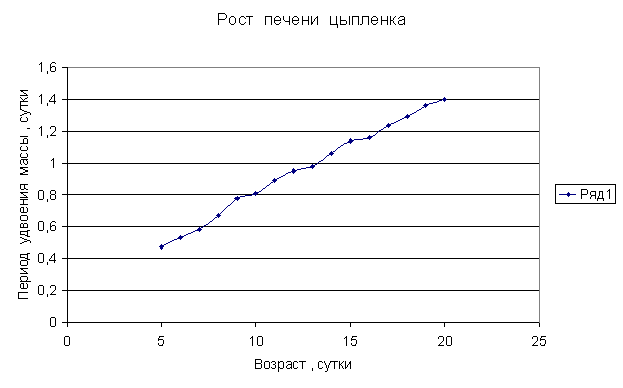

Приведенные
примеры показывают, что закон нормального роста __ это линейное увеличение периода удвоения массы с
течением времени.
Из аналитической
геометрии известно, что уравнение прямой линии в указанных выше координатах записывается следующим образом:
a = a0 + kt
(уравнение прямой с угловым
коэффициентом), a0 и
k __ параметры, т.е. величины, имеющие постоянное значение на
протяжении роста данного биологического объекта, но разные для разных
биологических объектов.
Слагаемое kt определяет замедление роста
биологических объектов и связанное с этим старение организма. Т.к. с каждой
единицей времени удвоение массы организма происходит все медленнее, неизбежно
наступит такой момент, когда период удвоения массы a0 +kt станет настолько большим, что организм не в состоянии осуществлять
физиологическую регенерацию. Клетки будут отмирать быстрее, чем
восстанавливаться. Это обстоятельство кладет биологический предел
продолжительности жизни живого организма.
Этот вывод
находится в соответствии с выводом геронтологов о том, что максимальный предел
продолжительности жизни человека не увеличивается с улучшением условий его
существования, а только увеличивается количество людей, приближающихся к этому
пределу, установленному природой для каждого живого организма.
Подставив в
формулу (1), с которой мы начинали наши рассуждения, вместо a0 значение a0 +kt, получим формулу (2), нарастания массы живого организма в функции от времени.
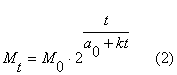
a0 __ начальный период
удвоения массы, k __ коэффициент замедления роста. По
этой формуле наращивают свою массу все живые организмы каждый со своими
параметрами a0 и k.
2
Кинетика роста злокачественной опухоли
Рассмотрим два частных случая формулы (2), когда
рост происходит с постоянным периодом удвоения массы.
1.
Рост популяции одноклеточных организмов в проточной
культуре. В этом случае формула (2) переходит в формулу (1)
2.
Злокачественный рост в начальной стадии своего развития.
Внедрение кинетики в онкологию связано с работами акад. Н. М. Эмануэля [2]. В его труде «Кинетика экспериментальных опухолевых процессов» проанализированы результаты, полученные разными исследователями, по росту большого количества злокачественных опухолей. В результате этого анализа он пришел к выводу о том, что в начальной стадии перевиваемых, экспериментальных опухолей выполняется экспоненциальный закон роста. Во многих случаях эта стадия является более или менее продолжительной. При некоторых опухолях и особенно при лейкозах экспоненциальный характер роста сохраняется вплоть до гибели животного.
Экспоненциальный характер наблюдается также и в случае роста метастазов опухолей.
По данным многих
авторов экспоненциальный характер роста сохраняется до образования 10 8¸10 9 опухолевых клеток.
В дальнейшем рост
опухоли отклоняется от потенциального закона, но нам важен именно начальный
момент ее развития.
По мере
увеличения массы опухоли ее внутренние и внешние участки оказываются в
неодинаковых условиях в отношении доступа к питательным веществам, часть
опухоли разрушается, происходит некроз и все это сказывается на общей картине
роста опухоли.
Итак, в начальной
стадии злокачественная опухоль растет по экспоненциальному закону. Это
означает, что если нормальные клетки растут по закону линейного возрастания
периода удвоения массы, т.е. по закону a =a0 +kt , все время
замедляя свой рост, старея, злокачественная клетка в какой-то момент
времени t1 прекращает замедлять свой рост и дает начало популяции
клеток, растущей с постоянным периодом удвоения массы a=a0+kt1=const. У старых людей этот период имеет большую величину, т.к. велико значение t1, но важно, что
больше он уже не увеличивается. Что конкретно происходит или в окружении
клетки, или в самой клетке, в результате чего замедляющая рост величина kt перестает увеличиваться,
математика подсказать не может. Но то обстоятельство, что злокачественная
опухоль в количественном отношении растет по тому же закону, что и популяция
одноклеточных организмов в проточной культуре, дает основание рассматривать
злокачественную опухоль как популяцию одноклеточных организмов, независимых от
организма.
Такой взгляд на
злокачественную опухоль подводит научную базу под направление в онкологии,
известное как микробная терапия рака.
Исследователями замечено, что некоторые
микроорганизмы и простейшие, попавшие в раковую опухоль, оказывают на нее
тормозящее действие или даже полностью
разрушают ее. Наиболее известными из них являются бактерия кишечной палочки и
трипаносома.
Если в одном и
том же жизненном пространстве существуют две популяции (в данном случае популяция раковых клеток и
микробная популяция), то одна из них
вытесняет другую и понятно, что преимущество будет за той популяцией, которая
быстрее размножается.
Так, может быть,
имеет смысл преднамеренное заражение злокачественной опухоли быстрорастущей микробной популяцией. Конечно, эта
популяция не должна наносить непоправимый
вред самому организму.
3
Зависимость снижения потенциала роста от нарастающей массы
Мы исследовали
закономерность нарастания массы от времени при нормальном и злокачественном росте.
Установили, что при нормальном росте период
удвоения массы увеличивается по линейному закону, а при злокачественном
росте период удвоения массы остается постоянным.
Исследуем теперь
зависимость этого периода от самой нарастающей массы. Но будет удобнее для
восприятия, если мы будем рассматривать не период, а величину ему обратную ![]() . Назовем ее потенциалом роста. Эта величина характеризует
способность организма к удвоению своей массы. Исследуем, как эта способность
меняется с нарастанием массы.
. Назовем ее потенциалом роста. Эта величина характеризует
способность организма к удвоению своей массы. Исследуем, как эта способность
меняется с нарастанием массы.
Обратимся сразу к экспериментальным
данным и построим график q=f( M).
В проточной
культуре биомасса удваивается с постоянным периодом a,
следовательно,
и величина ему обратная ![]() также будет
постоянной. Здесь каждая клетка
является самостоятельным организмом и ее рост не зависит от других клеток.
также будет
постоянной. Здесь каждая клетка
является самостоятельным организмом и ее рост не зависит от других клеток.
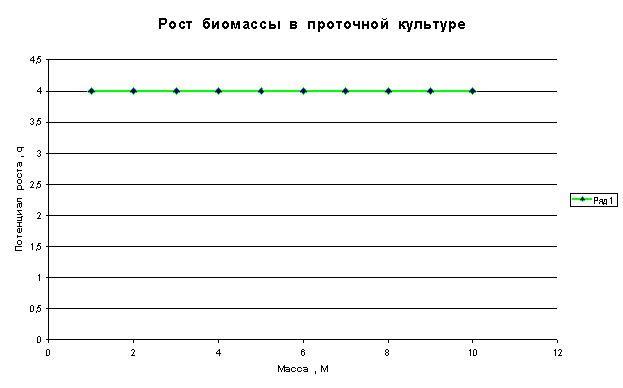
Графики зависимости q=f(M) для многоклеточных организмов имеют следующий
вид.
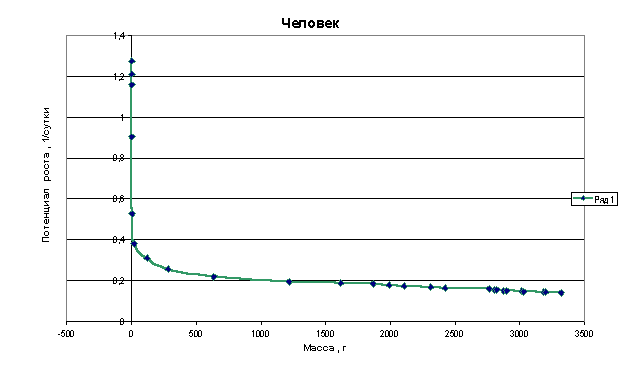
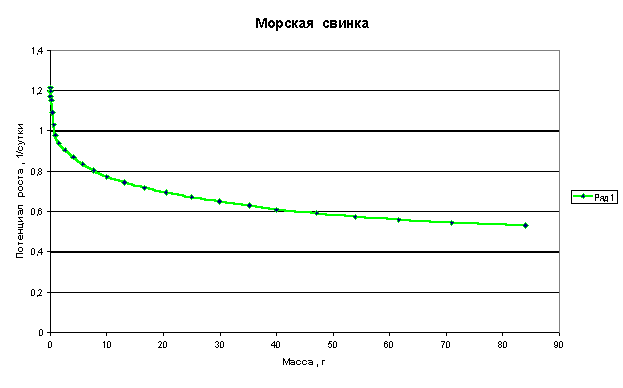


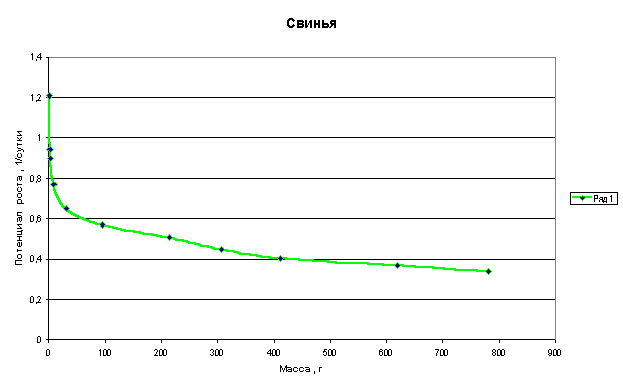
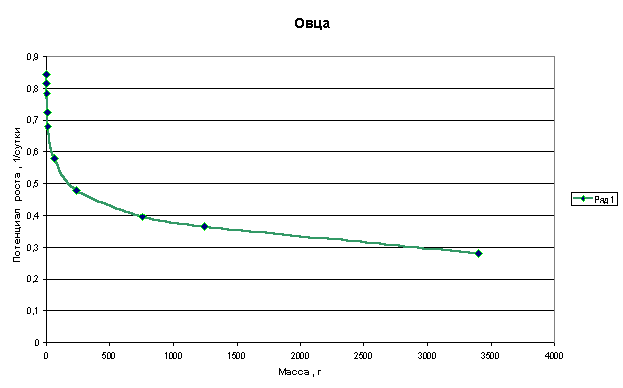
Из приведенных графиков видно, что потенциал роста или способность организма удваивать свою массу резко падает в самом начале роста, когда эта масса еще очень мала. В дальнейшем это падение уменьшается и впоследствии нарастание массы практически не влияет на величину потенциала.
Клетки, образующие многоклеточный организм, взаимодействуют друг с другом и тормозят рост друг друга. Из приведенных графиков видно, что это взаимодействие носит характер короткодействия, т.е. тормозящее рост действие проявляется только на небольшом расстоянии от клетки.
Каждая клетка взаимодействует только с теми клетками, которые расположены в непосредственной близости от нее. С клетками же, расположенными на большем расстоянии, она не взаимодействует, не хватает ее радиуса действия. И соответственно, другие клетки, расположенные дальше этого радиуса, не оказывают действия на эту клетку.
В начале роста, когда масса организма очень мала, все клетки взаимодействуют между собой, т.к. каждая клетка находится в радиусе действия других клеток. Ее рост затормаживается всеми другими клетками, и соответственно, она затормаживает рост других клеток.
На этом участке даже малейшее увеличение массы вызывает резкое снижение потенциала роста.
В дальнейшем все большее число клеток не достают друг до друга своим радиусом действия. Соответственно в организме уменьшается доля взаимодействующих клеток, снижение потенциала уменьшается. Эта доля продолжает уменьшаться и дальше по мере нарастания массы и со временем становится настолько малой, что практически не влияет на снижение потенциала роста.
Итак,
тормозящее рост действие клеток многоклеточного организма проявляется только на
коротком расстоянии от клетки. Об этом нам говорят графики зависимости q=f(M). Если бы это было иначе, то вид графиков был бы
иной.
Короткодействующие силы довольно распространены в природе. Это, например, силы связывающие между собой нуклоны в атомном ядре. Там поведение каждого нуклона определяется только теми нуклонами, которые находятся в непосредственной близости от него.
Короткодействующими являются также химические связи между молекулами твердых и жидких тел.
4
Гипотеза злокачественного роста
Предположим, что в результате каких-либо изменений в ближайшем окружении клетки она отдалилась со всех сторон от окружающих ее клеток на расстояние, большее, чем радиус короткодействия. В этом случае она не взаимодействует с соседними клетками и не испытывает от них тормозящего рост действия. Расстояние, о котором идет речь, очень мало и при некоторых условиях это отделение вполне возможно. Оно может произойти под влиянием самых разных причин: механического удара, трения о различные предметы, воспалительных процессов, действия различных химических веществ, радиации и т.д. Видимо поэтому так много причин, вызывающих злокачественный рост. Причин много, а суть одна - это пространственная изоляция клетки, отдаление ее от соседних клеток на расстояние, большее радиуса короткодействия. Логически можно предположить, что такая же изоляция может произойти в результате изменений в самой клетке, выразившихся в сокращении радиуса короткодействия самой клетки.
Клетки многоклеточного организма объединены между собой силами взаимодействия. Если бы этого не было, он представлял бы собой популяцию самостоятельных клеток, подобную популяции клеток в проточной культуре, и рос бы по закону этой популяции, т.е. без замедления роста. Но рост многоклеточного организма замедляется.
Эта разность между энергией роста популяции и энергией роста многоклеточного организма реализована в виде энергии связи клеток между собой. Аналогию мы находим в атомном ядре. Нуклоны, образующие ядро, связаны между собой силами взаимодействия. При разрыве этих связей энергия связи высвобождается в виде энергии ядерного взрыва.
Аналогично, при отделении клетки от соседних клеток энергия связи этой клетки высвобождается в виде энергии неконтролируемого роста и размножения этой клетки.
Вернуть клетку в прежнее положение невозможно, также как невозможно разломанный надвое кусок мела сделать вновь целым.
Поэтому процесс
злокачественного перерождения клеток необратим. Проверить изложенную гипотезу
можно, отделив какую- либо клетку покровной ткани на небольшое расстояние со всех сторон
от соседних клеток и пронаблюдать ее
дальнейшую судьбу. Если результат получится отрицательный, это будет означать несостоятельность гипотезы короткодействия.
В этом случае ее нужно или
подкорректировать, или отбросить. Но думаю, учитывая актуальность проблемы
злокачественного роста, предложенная гипотеза заслуживает экспериментальной
проверки.
ЛИТЕРАТУРА
1. Седова Г. П.
Закономерность роста биологических объектов. - Математическая морфология.
Электронный
математический и медико-биологический журнал. - Т. 5. - Вып. 2. - 2004. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/N-10-html/sedova/Sedova2004.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-10-html/cont.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-10-html/TITL-10.htm
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
2.
Эмануэль Н. М. Кинетика экспериментальных опухолевых процессов. – М.:
Наука, 1977. – 414с.
THE QUANTITATIVE ASPECTS OF MALIGNANT BODY HEIGHT
Sedova G. P.
Examination is devoted to studying of the quantitative aspects malignant body height. The kinetics of increase is surveyed masses of a metaphyte at normal body height, kinetics of body height of a malignant tumour, dependence of downstroke potential of body height from the increasing mass. The concept is introduced “short-range interaction”. The hypothesis of malignant body height is resulted.
Key words: malignant body height,
kinetics of increase of mass, kinetics of body height, short-range interaction.
г. Орел
Галина Павловна Седова
Поступила в редакцию 16.04.2008.