Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 7. -
Вып. 2. - 2008. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-18-html/TITL-18.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-18-html/cont.htm
УДК 530.1
СТРУКТУРНая НЕЛИНЕЙНОСТь в изотопном механизме рака
Ó 2008 г. Тукембаев Ч. А., Свиденко В. Н.
Найдено
аналитическое решение проблемы структурной нелинейности высокого порядка при
условии, что заданная однородная плотность есть трижды дифференцируемая функция
по dP. Решение является теоретическим
обоснованием многочастотного резонанса и изотопного механизма рака в терапии
нелинейными акустическими и электромагнитными волнами. Показано, что jamming-переход обусловлен критической точкой для
частиц растворителя и растворенного вещества.
Ключевые
слова:
нелинейные волны, многочастотный резонанс,
продольный и поперечный эффект
Доплера,
терапия рака, тяжелый азот.
1.
Введение
Проблема фазовых переходов и критических явлений стоит
под № 6 в "физическом минимуме" Гинзбурга [1]. Изучение фазовых
переходов, критических явлений (Орнштейна-Цернике) сталкивается с определенными
трудностями на основе теории Ландау, ренормгруппы, а также в кластерах и
фазовых переходах 3 рода [2-15]. Трудности вызваны сложностью изучения
изолированных и критических точек, в частности, критических индексов [5, 6].
Главным упущением перечисленных исследований [3-15] надо считать то, что,
сосредоточившись на поведении вещества вблизи критической точки, авторы не
приняли во внимание необходимость изучения химического потенциала и критическую
точку раствора [16], а она дает более полные представления о веществе,
поскольку включает в себя критическую точку вещества, как частный случай. В
работах [17, 18] предлагалось связать решение проблемы Пастера с критической
точкой, где хиральный избыток формируется под влиянием «сильного поля» Ландау
[16]. Это подверглось необоснованной критике [19], которая отрицательно
сказалась на решении проблемы Пастера, а ее решение по прошествии десятилетия нисколько
не продвинулось [20]. В отличие от работ [10-15] и,
особенно, [21] в исследованиях [22-26] установлено, что фазовый переход 3 рода есть
разделение частиц по зеркальному признаку. Тем самым, найден путь решения
проблемы Пастера [19].
Теория критических явлений Орнштейна-Цернике [2]
основана на выполнении ограничений [27], а ее применение связано с аномальной
диффузией [28]. Сжимаемость c(T)=(dV/dP)TN/q0V2, т.е. зависит от флуктуаций
среднего числа молекул N0 в
большом (по сравнению с корреляционной длиной) объеме V, где q0=N0/V0 –
плотность среднего числа частиц в объеме. Для вывода уравнений
Орнштейна-Цернике требуется накладывать ограничения на корреляционную функцию,
что обусловлено избыточностью формулы из-за плотности частиц q0. Умножив
c(T) на
V/N, получаем
сжимаемость в ее классическом виде c=-V-1dV/dP.
Нелинейные волны состоят в
"физическом минимуме" под № 11
и, как структурная нелинейность,
определяются в структурно-неоднородных средах из уравнений гидродинамики. Это уравнения
волн Бюргерса, Хохлова-Заболотской, наследственных сред Вольтерра и различные
модификации этих уравнений с гистерезисом, содержащие скорость звука в виде с3
[29]. К ним по принадлежности
к гистерезису относятся явления с памятью формы на ферромагнетиках [30] и
сегнетоэлектриках [4]. Актуальность анализа прямых и обратных задач волновых
задач [29, 31] обусловлена
конструированием нелинейных литотриптеров [32] и устройств электромагнитной
терапии [33, 34], разрушающих конкременты и раковые клетки как неоднородности.
Нелинейные волны ограничены
слева линейными волнами, определяемых производной ¶P/¶r=с2 – const. С ростом давления для волн
сжатия производная (¶2V/¶P2)S>0 при постоянной энтропии S, но для волн разрежения (¶2V/¶P2)S<0 [35], поэтому надо определиться с независимой
переменной в этой производной. Нелинейность обусловлена макроскопическими
упругими свойствами, как разложение внутренней энергии E слабо деформированной среды в
степенной ряд по инвариантам тензора деформаций [36]; коэффициенты при
квадратичных членах разложения являются линейными модулями упругости, при
кубичных членах – нелинейными модулями Ландау. Модуль упругости e=-V0dP/dV и сжимаемость c=-V0-1dV/dP – это обратные величины,
произведение которых ec=1, чего нельзя
сказать о вторых ¶2P/¶V2,
¶2V/¶P2
и третьих производных ¶3P/¶V3,
¶3V/¶P3.
Индексом "0" отмечены
переменные однородной среды. В отличие
от нелинейных модулей Ландау будем искать решение задачи структурной нелинейности в зависимости от производных ¶2r0/¶P2 и ¶3r0/¶P3 для определения нелинейной длины волны [29] и многочастотного
резонанса на неоднородностях. Практическое применение решения служит
электромагнитной терапии рака [33, 34], являющейся альтернативой нелинейным
литотриптерам, а также в вынужденном комбинационном рассеянии (ВКР) [37].
Падение волны с крутым ударным фронтом на первичную
опухоль приводит к рассасыванию метастазов. При этом возникает разрушение
субклеточных структур гигантскими градиентами давлений и ускорениями на фронте
за счет инерционных сил, обусловленных пространственной неоднородностью
плотности, сдвиговой упругости, которая очень чувствительна к патологическим
изменениям ткани. Например, в опухолевой ткани сдвиговая упругость
увеличивается на 2-3 порядка, в то время как другие параметры (плотность среды,
скорость звука) изменяются лишь на несколько процентов [29, c. 89]. В дополнение к [29] подчеркнем важное
обстоятельство. Сдвиговая вязкость x по сравнению с объемной вязкостью h связана с изменением поверхности, что напрямую
отражается на сдвиговой упругости. Рассматриваемая однородная плотность
становится неоднородной плотностью. Поэтому надо считать, что сдвиговая
упругость зависит от поверхностного натяжения так, что патологические изменения
ткани определяются изменениями ее поверхности.
Возникает вопрос о химическом составе примеси, но в
настоящее время химический состав нормальных и опухолевых клеток различается
только по концентрациям. На это указывает падение pH внутриклеточной жидкости опухолей ниже 7.0 [38, 39].
Что вызывает изменение концентрации водородных ионов, если клетки организма не
облучаются и наличие радиоактивных элементов и их следов в организме
физико-химическими анализами не регистрируется? Тем не менее, на уровне тонких
методов спектрального анализа наблюдается различие в спектрах опухолевых и
нормальных тканей. Однако идентифицировать вещество, возбуждающее рак не
удается, поэтому приходится считать примесь "фантомом рака".
2. Изотопный механизм рака
Мы не затрагиваем изменений ДНК и субклеточные
структуры, они учитываются как неоднородности. Нас интересуют только
физико-химические свойства неоднородностей, по которым надо определить
химико-изотопный состав. Внедрение "фантома рака" отражается на
изменении механических характеристик ткани и выражается в резком росте
сдвиговой упругости. С точки зрения механических характеристик опухолевая ткань
представляет собой совершенно иное тело, так как сдвиговая упругость отличается
на 2-3 порядка по сравнению со сдвиговой упругостью нормальных тканей, судя по
измерениям [29]. Неужели совершенство физических приборов не позволяет
идентифицировать "фантом рака", как вещество, свойства которого
проявляются в спектрах и механических характеристиках? Или же это вызвано
недостаточностью знаний и непониманием того, что скрывают в себе спектры и сдвиговая
упругость? Для ответа на этот вопрос, необходимо исследовать структурную
нелинейность в зависимости от концентрации.
Изучению критической концентрации посвящен новый
фазовый переход типа "jamming" (затор или пробка) и предложен вниманию в
авторитетном журнале Nature. Он
обусловлен критической концентрацией в коллоидных системах, конденсированных
средах и гранулах [40-50]. Анализ этих работ выявил, что авторы не взяли за
основу jamming-перехода давно разработанную критическую точку
раствора [16]. В перечисленных выше работах упоминается в ссылке теория
упругости Ландау [36]. Единственной тому причиной надо считать то, что физика
фазовых переходов изучала критическую точку вещества и оставила в стороне
критическую точку раствора.
Тяжелый азот давно применяется биологами и медиками в
качестве меченого атома [51]. В [52] 15N добавлялся в питание и выявлено, что содержание
аминокислот резко отличается от содержания аминокислот контрольной группы. К
сожалению, в 1983 году исследователь [52] не связал данный факт с токсичностью
тяжелого азота для молодого развивающегося организма, что ему было подсказано в
дальнейшем. В [53] расчетным путем была определена концентрация 15N в атмосфере, которая в основном состоит из азота, а
это 78 %. Азот состоит из 2 изотопов: 14N – легкого азота и 15N – тяжелого азота. Стандартное содержание каждого
изотопа известно, поэтому концентрация 15N в азоте равна 10.95‰. Именно это значение
концентрации совпало с критической концентрацией вымирания популяций, найденной
опытным путем, но нормальное значение равно 7.5‰ [54]. Этому объяснение
простое. Если концентрация 15N в мембране клетки больше 10.95‰, то солнечный свет на
всей спектральной линии азота за счет естественного уширения не будет проникать
внутрь клетки, а потому прекратится фотосинтез внутри клетки.
Роль оксида азота NO в организме
освящена в обзорах [55-66]. Однако остается неизвестным признак, по которому
азот в NO надо разделять на неорганическую и биологическую
составляющие. Это важно, поскольку продуктом неорганического азота является не
только N2O, но и
вещество, обуславливающее непроницаемость мембраны. Основываясь на изложенном,
для идентификации веществ в наших работах используются физические методы в
неразрешенных местах новых явлений.
Для определения признака биологического и неорганического азота надо
опираться на изотопный состав оксида азота. Достаточно определить вязкость
оксида азота в зависимости от изотопного состава NO. Вязкость оксида азота h зависит от изотопов азота в нем так, что вязкость 14N16O меньше вязкости
15N16O. При 20 °C для 14N16O h=189.9×10-7 кг/м×с, но для 15N16O h=192.85×10-7 кг/м×с [66]. Именно большая вязкость 15N16O обуславливает,
во-первых, больший контакт 15N16O со стенками
кровеносных сосудов при транспорте крови по сравнению с 14N16O и сдвиговые
напряжения; во-вторых, изотоп 15N является фермионом, поэтому более химически активный,
чем бозон 14N. Все это
способствует присоединению 15N16O к химическим
элементам или соединениям на границе ткани сосуда, принадлежащих этой ткани, и
образовать с ними прочное химическое соединение в коллагене. В результате
сдвиговая упругость стенок сосуда увеличиться, что выразится атеросклерозом, а
затем будет обнаруживаться в апатите и коллагене костей. Ранее этот факт
исследователи не могли заметить, так как не принимали во внимание изотопы
азота. Однако канадским ученым удалось обнаружить высокую концентрацию 15N в останках вымерших популяций. В результате появилось
еще одно доказательство о роли тяжелого азота как причины рака. Это вкупе с
захватом p--мезона тяжелым азотом и критической температурой N2O дает
возможность надеяться на превращение гипотезы в теорию. В этой связи актуально
изучение содержания изотопа 15N, NO и N20 в
экологии [67, 68].
Обобщая опыт применения гипертермии в клинике, Европейское Общество
иммунодефицита (INS) установило порог гипертермии,
равным 38.5 °С. Интервал 38.5-39.0 °C особо опасен из-за роста объема опухоли скачком.
Может произойти разрыв опухоли, поэтому данный интервал стараются как можно
быстрее пройти при нагреве и при охлаждении после сеанса гипертермии. Вне этого
интервала опухоль возвращается к своим размерам. Принимая во внимание
полупроницаемость мембраны, следует считать, что скачок объема в интервале
38.5-39.0 °C может быть обусловлен только
большими градиентами давления неизвестного газа. Так как гипертермия внутри
интервала 38.5-39.0 °С проявляется в виде скачка объема опухоли, то в этом интервале опухоль
содержит неизвестное вещество, для которого полупроницаемая мембрана становится
непроницаемой: система замкнута.
В работе [69] установлено, что искомым веществом является закись азота N2O, при этом
критическая температура N2O Tc=38.75 °С точно попадает в центр интервала 38.5-39.0 °С. Значит, фазовое превращение закиси азота при
переходе через критическую температуру Tc вызывает скачок объема. При охлаждении в конце сеанса
гипертермии скачок объема в интервале 38.5-39.0 °C гласит о неуспешном лечении, так как N2O и порождающее N2O вещество
остались в опухоли. Высокая концентрация N2O во
внутриклеточной жидкости проявляется в виде скачка объема внутри интервала
38.5-39.0 °С, поскольку возникают
флуктуации объема и температуры вблизи критической точки N2O [70, 71].
Закись азота, как наркотик, отравляет клетку. Так как имеет место скачок объема
N2O, то, значит,
мембрана опухолевой клетки стала непроницаемой для закиси азота. В свою
очередь, N2O является конечным продуктом оксида азота NO [70, 71].
Способ распознавания биологического или неорганического азота в составе
аминокислот предложил Пастер. Все природные аминокислоты входят в состав белков
и являются L-изомерами в отличие от D-аминокислот, которые также встречаются в природе, но
не в белках, а в оболочках бактерий и структурах многих антибиотиков.
Традиционные методы измерения оптической активности содержат главное препятствие
в измерении l- или d-вращения плоскости поляризации света, соответственно,
L- или D-изомерам.
Препятствие в том, что невозможно in vitro
заполнить кювету длиной 10 см внутриклеточной жидкостью опухоли. Приходится
ограничиваться малыми объемами жидкости, но тогда надо решить проблему Пастера.
С учетом этого необходимо иметь ответы на вопросы. Какими квантовыми свойствами
должен обладать азот, чтобы в результате этих свойств появился биологический
азот и какие должны быть ядерно-физические свойства азота, чтобы он стал
неорганическим азотом?
Ответ на эти вопросы дан в работах [72, 73]. Биологическим азотом
является легкий изотоп азота 14N, который порождает 3-валентные соединения, но
неорганическим азотом – тяжелый изотоп азота 15N, который образует 5-валентные соединения в нормальном
состоянии. Из тяжелого азота 15N получается цианамид в порах мембраны, что делает ее
непроницаемой [73]. Температура плавления цианамида равна 42.8 °С, что и вынуждает разогревать больные ткани до 43.0 °С в сеансах гипертермии. Это доказательство основано
на следующем. Во-первых, эффект пионной терапии опухоли заключается в ядерном
взаимодействии пионов-p- и протонов с 15N, тогда как пион и протон не могут преодолеть
квадрупольный барьер 14N в
пределах энергии, необходимой для рождения пионов [74], используемых для
терапии, во-вторых, вымирание популяций начинается тогда, когда содержание 15N в организме равно 10.95‰ (промилле), а это есть
критическая концентрация, равновесная содержанию 15N в атмосфере. Кроме давления, температуры и объема в
критической точке, исследуется критическая концентрация для системы с
переменным числом частиц [16]. Различие в массах 14N и 15N обуславливает изотопический эффект
Максвелла-Рейнольдса: разницу в критических температурах [74, т. 1, c. 766] и может быть обнаружен, так как подается
вычислению [75], в-третьих, спин, магнитный и квадрупольный моменты 14N, а это бозон, вынуждают к образованию L-изомера в паре с другим изотопом 14N.
Следует также отметить, что если в паре с 14N другим изотопом будет тяжелый азот 15N – фермион, то образуется D-изомер, т.е. найдена причина, по которой разделяются
зеркальные изомеры, как решение проблемы Пастера. Математическим обоснованием
служит элемент объема dV=(g)1/2dxdydz, где положительному якобиану g>0 соответствует dV>0 в правой системе координат и D-изомер. Для наглядности можно применить метод [76],
позволяющий найти изменения для разных изотопов. Если g<0, то dV2<0 и получаем L-изомер, где dV
принимает комплексное значение, как частица, поверхность которой имеет
отрицательную кривизну. Это означает, что внутри объема V,
рассматриваемого в правой системе координат, появилась L-частица с комплексным элементом объема dV,
компоненты метрического тензора которого выражены в левой системе координат.
Оптически активными являются парамолекулы, но ортомолекулы оптически неактивны.
Основываясь на боковой волне [35] в преломленных лучах
[77] и результатах наших исследований [78, 79], дадим объяснение тому, как свет
проникает внутрь нормальной клетки в виде боковой волны в оптическом диапазоне.
При этом, как известно [79],
внутрь опухолевой клетки боковая
волна не проникает, причиной чему является структурная нелинейность,
выражающаяся в высокой концентрации тяжелого азота 15N на поверхности клетки по сравнению с содержанием
тяжелого азота в атмосфере Земли. Причем, если концентрация 15N на поверхности клетки больше, чем концентрация 15N в атмосфере, то свет не проникнет внутрь клетки не
только на линиях 15N, но и на всей
ширине линии азота, так как естественное уширение линии 15N перекроит линию легкого азота 14N, а, следовательно, всю линию азота. В этой связи
субклеточные субстанции лишатся света на жизненно важной линии азота в
оптическом диапазоне. Это значит, что прекратится фотосинтез аминокислот и
белков из биологического азота, основой которого является легкий азот 14N, но его заменит неорганический азот 15N, образующий и трех- и пятивалентные соединения.
Данный факт преломления соответствует переходному излучению [80].
Настоящая работа посвящена теоретическому обоснованию структурной
нелинейности на примере изменений механических и физико-химических свойств
между нормальными и опухолевыми клетками.
3. Отрицательный элемент объема
Масса M и объем V являются функциями двух
разных переменных. Масса, какими бы не были P, V и T, зависит от числа частиц N0 в
заданном объеме. В однородном теле средняя плотность r0=M0/V0=m0N0/V0. В рамках молекулярной физики масса M0=m0åNi, i=1, …, K, определяется числом отдельных частиц Ni в объеме V0 и массой отдельной частицы, молекулы m0=const. Объем V это
функция координат x, y, z. Поскольку
m0=const, то при
дифференцировании m0 выносится вне знака
дифференциала m0d(N0/V0). Однако выражение под дифференциалом содержит
неопределенность. Отношение N0/V0=q0 представляет
собой плотность частиц с массой m0 в объеме
V0.
Дифференцирование по объему не вызывает затруднений, если элемент объема dV=dxdydz. В
общем случае, элемент объема определяется якобианом [81], который может быть
равен нулю. Тогда получаем особую точку. Неравенство элемента объема dV нулю и дифференцируемость являются только
достаточными условиями трансформации однородной плотности r0 в
неоднородную плотность r¢.
Средняя плотность r0=m0q0
выражается через плотность числа частиц в объеме – q0=N0/V0. Когда q0 зависит только от объема V, то возможно найти лишь производную ¶q0/¶P=(¶q0/¶V)(¶V/¶P), считая, что N0=const. Изменяется элемент объема dV, занимаемый молекулой. Однако, числитель
в q0=N0/V0 остается неопределенным, так как число
частиц åNi=N0 не поддается счету. Например, для одного моля газа N0 равно числу Авогадро NA=6.022×1023 моль–1. Иначе, число частиц фактически является неизмеримым
множеством для современных физических приборов, поэтому нуждается в нормировке
путем деления на общее число частиц N0.
В результате нормировки получим сумму
концентраций ni=Ni/N0, равную 1, что осуществимо на практике.
Тот же самый результат мы получим, дифференцируя числитель отношения N0/V0 по числу частиц, как ¶N0/¶N0=1 (dx/dx=1). Следовательно, чтобы преобразовать
несчетное множество частиц в объеме, надо перейти к концентрациям путем
нормировки или продифференцировать числитель отношения N0/V0 по числу частиц N. Производная в знаменателе (V0)¢ берется по криволинейным координатам x1, x2, x3, связанных с прямоугольными декартовыми координатами (x, y, z) формулами ![]()
![]()
![]() и равна якобиану
и равна якобиану
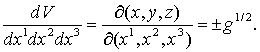
Квадрат якобиана
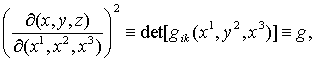
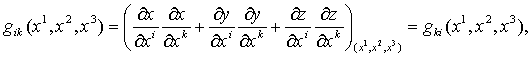
(i, k=1, 2, 3),
функции gik(x1, x2, x3) –
компоненты метрического тензора. В правой системе координат якобиан ¶(x, y, z)/¶(x1, x2, x3)=g1/2>0, но в левой системе координат g1/2<0,
по определению [81].
Для перехода от однородной плотности к
неоднородной плотности, по сути, необходимо применить правило Лопиталя к
плотности частиц q0, равному
отношению N0/V0. Тем самым, однородная плотность r0 становится неоднородной плотностью r¢=(r0)¢/(V0)¢, если
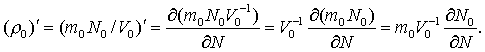
Иначе говоря, в однородном газе равенство частной производной ¶N0/¶N по переменной числа частиц N, означает возможность дифференцирования
по всему числу частиц. Поэтому соответствие нормировке есть ¶N0/¶N=1. Тогда классическое определение
плотности r=DM0/DV0@dM/dV совпадает с неоднородной плотностью r¢ и имеет вид
![]()
а производная плотности частиц q¢=dN/dV, где индекс "0"
при r теперь можно опустить. Следовательно,
неоднородная плотность есть r¢=m0q¢. Для однородного газа m=m0 вынесено за знак дифференциала, так как считаем массу молекулы m0=const,
что справедливо для однородного газа.
Таким образом, для перехода от однородной плотности к
неоднородной плотности необходимо, чтобы все частицы в объеме были различимы и
функция q дифференцируемой по
числу частиц, т.е. должна быть гладкой. Если в некоторой точке dV меняет знак так, что dV>0 становится dV<0,
то возникает разрыв производной в точке на левостороннюю и правостороннюю
производные. Когда dV=0,
то получаем особую точку. В квадратичной
метрике разрыва производной из-за перемены знака нет. Возведение в квадрат,
т.е. dV2, устраняет
такую особенность из-за потери знака (dV2)1/2=|dV|. Следовательно, в квадратичной метрике частицы с
отрицательными элементами объема dV<0 считаются частицами с положительным элементом объема dV>0, но
остается точка, где dV=0,
как особая точка. Особенности такого рода, где (¶P/¶V)T обращаются в нуль, требуют отдельного
изучения и не ясно насколько теория Ландау претерпит изменения [16, 2 изд].
Однако, из того, что теория Ландау пренебрегает частицами dV<0, следует пересмотреть вопрос о
правильности термодинамических неравенств в плане равенства смешанных
производных в точке с односторонними производными, где dV меняет знак.
Теорема 1. Знак ¶P/¶V
соответствует знаку элемента объема dV.
Доказательство.
Давление P зависит от объема V и температуры T. Из дифференциалов
dP и dV независимой
переменной является только элемент объема dV, который может быть как
положительным, так и отрицательным в зависимости от знака якобиана: выбора
правой или левой системы координат [81]. В таком случае для волны сжатия производная ¶P/¶V>0, если dV>0. Тогда волне разрежения ¶P/¶V<0
соответствует dV<0. Теорема доказана.
Ранее считалось, что волне разрежения
соответствует DP<0, а dV может быть только положительным, чем и был обусловлен
отрицательный результат [82-88], так как для ячеек разностной схемы не
учитывались dV<0. Теперь такая некорректность, в том числе и для (¶2V/¶P2)S [35], преодолена.
Физическая суть отрицательного элемента объема в том, что под этим понимается
отрицательная кривизна на плоскости [89]. В пространстве кривизна k=|r²| положительная величина, но "dV<0
отрицательно кручение t=|r¢r²r¢²|, r –
радиус-вектор [81], поэтому
заданный в области G объем V равен SdV+S(-dV)=V1-V2. Значит, вопрос об адекватности исходных уравнений
моделям на ячейках разностных схем [90] решается с учетом V=V1+|V2|.
ТЕОРЕМА 2. Если dV<0, то отрицательных температур нет.
ДОКАЗАТЕЛЬСТВО. Термодинамическое неравенство [16, c. 83-86] справедливо только для частиц dV>0,
т.е. до тех пор, пока нет различия частиц по знаку dV в фазовых переходах 1 и 2 рода. Такое термодинамическое неравенство становится
некорректным в фазовых переходах 3 рода, поскольку требуется отличать частицы
по знаку dV,
как зеркальные частицы [22-26]. Тогда термодинамическое
неравенство приобретает новый вид
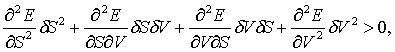
где
вторые смешанные производные по ¶S и ¶V неравны друг другу, т.е. для частиц с разным знаком dV односторонние вторые смешанные производные
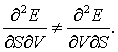
Тем самым, в термодинамических неравенствах (21,5) и (21,6) [16]
устраняется двузначность по отношению к T и (¶P/¶V)T<0, поскольку на участках изотерм с положительным
наклоном будут устойчивы состояния, у которых dV<0. Причем температура всегда положительная
величина: в формулах вместо T<0 надо принять dV<0. Именно поэтому, по сравнению с [16], выбор в [22-26]
был сделан в пользу отрицательного элемента объема dV<0, следовательно,
отрицательных температур в природе нет. Теорема доказана.
В отличие от [2, 27] для установления фактора,
вызывающего аномальную диффузию [28] и явление [91], умножим c на m0 – массу
одной частицы и получим массовую сжимаемость m0c=-r0dV/dP, где
r0=m0N/V0. Полагаем, что r0 трижды
дифференцируемая функция и число частиц в объеме является счетным множеством:
зеркальные частицы различимы по знаку dV. Тогда нелинейная волна ограничена на правой границе
следующим образом.
ТЕОРЕМА 3. Для существования
нелинейной волны и продольного эффекта
Доплера необходимо и достаточно, чтобы "x>0 производная ¶2r0/¶P2 была ограничена пределом прочности s/Dl при максимуме удлинения Dl.
ДОКАЗАТЕЛЬСТВО. В неоднородной
среде
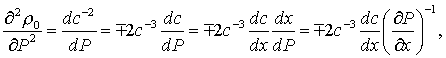 (1)
(1)
где
знак соответствует волнам сжатия или разрежения, согласно теореме 1.
Векторам касательной t, главной
нормали n и бинормали b соответствуют x=x1, x2, x3. Вторая производная r² кривизны k определяется через градиент скорости w=dc/dx и как проекция на соприкасающуюся плоскость есть
изменение скорости cºu по главной
нормали n к ее направлению по касательной t.
Производная du/dx (м/с×м=1/с) является, по сути, варьируемой в
зависимости от x
частотой, что характеризует продольные
колебания упругих волн и продольный эффект Доплера.
Предел эластичности f=Ds/Dl ограничен относительным удлинением Dl/Dx, при котором происходит разрыв элемента объема на две частицы. Если градиент давления ¶P/¶x>f, то произойдет разрыв dV на два элемента объема.
Производная ¶2r0/¶P2<f и при росте ¶P/¶x ведет себя как малая конечная
величина. Значит, продольные колебания
объема определяются существованием нелинейной волны, продольного эффекта Доплера,
градиентами скорости и давления при условии, что ¶P/¶x£f. Теорема доказана.
Таким образом, при росте ¶P/¶x возникает деление элемента объема всякий раз на пару частиц по мере того,
как ¶P/¶x=f. Поэтому, если ¶P/¶x>f, то внутри
каждого элемента объема останутся только молекулы. Частицы одного сорта имеют
одинаковый предел эластичности, поэтому частицы делятся лавинообразно в
определенном направлении (разлома среды), где s минимально, с характерным излучением
волн. Это объясняет нелинейную акустику, эффект литотриптера [29, 32],
аномальную диффузию [28] и явление [91], так как остаточные напряжения горной
породы обуславливают градиент давления, приводящий к разлому породы по мере
превышения предела прочности породы градиентом давления на участках Dl. Проникновение частиц в другую среду в виде нелинейной волны – это есть
аномальная диффузия. Деление конкрементов и раковых клеток с помощью
литотриптера напрямую зависит от крутизны ударного фронта, а точнее от Ds/Dl=f, как предела прочности конкремента или
раковой клетки на растяжение. Тем не менее, убывание ¶2r0/¶P2 сопровождается ростом ¶3r0/¶P3.
ТЕОРЕМА 4. Независимо от знака u
рост ¶3r0/¶P3 неограниченный.
ДОКАЗАТЕЛЬСТВО. Дифференцируем
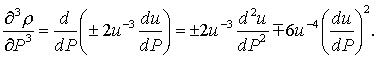 (2)
(2)
Из условия трижды дифференцируемости r0 постоянная ¶3r0/¶P3=±2B,
поэтому условию u>0, если ¶3r0/¶P3=2B, соответствует уравнение
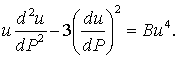
Последовательные замены v(u)=u¢(P) и w(u)=v2 дают уравнение 1 порядка
![]() (3)
(3)
Поскольку знак при w отрицательный, то рост ¶3r0/¶P3 неограничен. Если
u<0 знак при w левой
части уравнения (3) не изменится, а потому ¶3r0/¶P3 растет. Для волны разрежения ¶3r0/¶P3=-2B, поэтому v становится мнимой величиной.
Тогда производная ¶3r0/¶P3 неограниченно растет, но по периодическому закону, и
обусловлена ростом скорости. Теорема
доказана.
ТЕОРЕМА 5. Пусть заданы ¶P/¶x=a(x), (¶P/¶x)2=a2(x), ¶2P/¶x2=b(x) и y(x)=u¢/u. Тогда градиент w=d2u/dx2
ограничивает нелинейную волну справа и в зависимости от знака ¶3r0/¶P3=±2B определяется решением уравнения
Риккати
![]() (4)
(4)
ДОКАЗАТЕЛЬСТВО. Согласно формулам (1) и (2)
производная
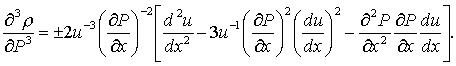
Если
приравнять первый сомножитель к постоянной ±2B, то с
увеличением x получаем убывание нелинейной волны, так как (¶P/¶x)-2. Второй
сомножитель в квадратных скобках дает закон изменения градиента w=u²(x) в зависимости от (¶P/¶x)2,
¶2P/¶x2 и ¶P/¶x, который
смыкается своей левой границей с правой границей нелинейной волны. Приравнивая
сомножитель в квадратных скобках к постоянной ±2B, получаем
следующее уравнение
![]()
Подстановка
y(x)=u¢/u приводит к уравнению Риккати
![]()
Теперь,
если сомножитель в квадратных скобках взять со знаком "-"
и приравнять его к постоянной ±2B, то в уравнении Риккати
знаки при свободном члене 2B только поменяются на "±". Теорема доказана.
Производная d2c/dx2
выражается отклонением в поперечном направлении. Такое отклонение происходит в
спрямляющей плоскости по бинормали b в направлении касательной t, а потому знак может быть как положительным, так и
отрицательным. В случае положительного знака элемент объема dV, построенного на векторах t, n и b, будет положительным. Если dV<0, то в тройке векторов t, n и b пара
векторов поменяется местами, а это значит, что отрицательному элементу объема dV соответствует левая система координат. Именно поэтому
¶3r0/¶P3=±2B. Отклонение в поперечном направлении есть отклонени в
спрямляющей плоскости, что обуславливают поперечный эффект Доплера и вращение
плоскости поляризации волны.
5. Нелинейные колебания и многочастотный резонанс
Для разрывной функции справа и слева от точки разрыва
надо взять n членов в суммах ряда Фурье, которые в точке разрыва
равны нулю, а именно так надо трактовать фазовый переход n рода. В
точке перегиба четные производные равны нулю, и ее отделяют от разрыва только
неравенство нулю ее нечетных производных. Тогда остается изучить точку перегиба
на устойчивость, так как неустойчивости будет соответствовать разрыв [22-26].
Схему применения метода продемонстрируем для
сжимаемости, поскольку она тесно связана с теорией критических явлений
Орнштейна-Цернике. Умножим массовую сжимаемость m0c=-r0dV/dP на постоянное число w02, равное квадрату частоты w0=(s/m0)1/2
гармонических колебаний. Тогда sc=-w02r0dV/dP, так как s - это коэффициент
упругости по закону Гука или константа силовых связей молекулы. Фазовому переходу 2 рода соответствует, как известно,
скачок сжимаемости, когда ¶P/¶V=0.
Принимая z=sc и считая r0 кубической нелинейностью, трижды
дифференцируем левую и правую части выражения z=-w02r0dV/dP:
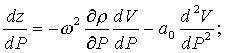 (5)
(5)
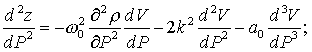 (6)
(6)
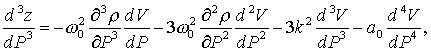 (7)
(7)
где
a0=w02r0, k2=w2(¶r/¶P)=w02/u2, (k2)¢=(w02/u2)¢=-2w02u-3u¢=-2k2u¢/u, u¢=du/dP, u¢/u=y, (k2)²=-2k2u-1u²+6k2(u¢/u)2, k - волновой вектор. Причем, k2>0, (k2)¢<0 для волн сжатия, т.е. "dV>0, но k2<0, (k2)¢>0 для волн разрежения dV<0. В отношении (k2)² можно только полагать инверсию знака, но из трижды
дифференцируемости r0
производная (k2)²=±w02/2B есть постоянная величина, (k2)¢ – линейная функция и k2 – квадратичная функция. Рассмотрение системы в форме
(5)-(7) обусловлено тем, что доступны измерениям только w0 и r0.
Система (5)-(7) из 3 уравнений с 4 производными dV/dP, d2V/dP2, d3V/dP3 и d4V/dP4 в правой
части. В таком виде число производных соответствует фазовому переходу 4 рода,
поэтому для изучения фазового перехода 3 рода будем считать производную d4V/dP4=0. Тем
самым, систему (5)-(7) можно рассматривать относительно точки квазиперегиба Eq,
тогда производную d2V/dP2 считаем малым параметром e. Если e=0, то точка квазиперегиба Eq будет точкой перегиба Eex, так как все четные производные равны нулю. В случае e¹0 точка квазиперегиба Eq может быть особой точкой.
ТЕОРЕМА 6. Точка перегиба системы (5)-(7) есть центр
симметрии и линейных колебаний только тогда, когда dV<0.
ДОКАЗАТЕЛЬСТВО. Согласно принятым обозначениям и
условиям в точке перегиба d2V/dP2=d4V/dP4=0 система (5)-(7) примет следующий вид:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Исключив
dV/dP и d2V/dP2 в правой
части системы (8)-(10), получим уравнение 3 порядка, соответственно для волн
разрежения (+) и сжатия (-)
![]() (11)
(11)
так
как для волн сжатия k2>0, (k2)¢<0, (k2)²>0 "dV>0, но для волн разрежения k2<0, (k2)¢>0, (k2)²<0 "dV<0. Подстановкой z¢=w в (11) дает уравнение 2 порядка
![]() (12)
(12)
поэтому колебания возникают только, когда dV<0. Теорема доказана.
Значит, колебания на основной гармонике (k1, k2)
уравнения (12) имеют место только для отрицательного элемента объема
(электрона). Тем не менее, колебания возможны на
побочных гармониках при любом знаке уравнения (12).
ТЕОРЕМА 7. Нелинейные колебания на
побочных гармониках не зависят от знака корней k1 и k2 соответствующего уравнению (12)
характеристического уравнения и определяются его детерминантом
![]() (13)
(13)
ДОКАЗАТЕЛЬСТВО. В детерминанте корням k1 и k2 знак
"-" соответствует
волне разрежения, а знак "+" – волне сжатия. Детерминант D=0, если
корни k1=k2 уравнения (12), т.е. когда 2 поверхности параллельны.
Пара корней в (13) k2=0,
поэтому получим нелинейное уравнение 2 порядка относительно переменной k2
![]() (14)
(14)
Замена
k2=y приводит к
известному нелинейному уравнению 2 порядка
![]()
решение которого дано в [92, с. 491]. Возврат к переменным системы
(8)-(10), дает ее решение на побочных частотах в зависимости от w0 и r0 при k1=k2.
Помимо известных методов [93], изучение устойчивости
уравнения (14) более эффективно с помощью обобщенного критерия Гурвица [94].
Зададим (k2)¢ и (k2)² в виде интервальных чисел [(k2)¢]=[l¢] и [(k2)²]=[l²] и
преобразуем уравнение (14) в полином с интервальными коэффициентами
![]() (15)
(15)
![]() (16)
(16)
Теперь,
вычисление определителей матрицы Гурвица сводится к вычислениям по правилам
интервального анализа, откуда находим, какими должны быть интервалы [(k2)¢] и [(k2)²], определяющие область устойчивости.
Решение уравнения (16) находим по
формуле Кардано, где можно задать вместо интервальных коэффициентов [y¢] и [y²] их средние значения и границы интервалов. Так как
детерминант уравнения (16) для волн сжатия D>0, то ему соответствуют одно действительное и два
комплексных корня. Дополнительно к корням k1=k2 получаем
6 корней k3, k4, k5, k6, k7 и k8, являющихся ненулевыми волновыми векторами, среди
которых, по крайней мере, 4 комплексных корня определяют многочастотный спектр
резонанса. Для волны разрежения D<0, поэтому каждому отрицательному корню lj
соответствует пара мнимых корней kj, что вызывает колебания. Следовательно,
точка перегиба системы (8)-(10) является центром симметрии Ли, порождающего
нелинейные колебания на побочных частотах или модах ВКР, соответствующих
комплексным корням уравнения (15). Теорема доказана.
Теоремы 6 и 7 дают объяснение резонанса на
побочных гармониках в ВКР [37], акустоэлектронике [31], электромагнитной
терапии [33, 34] и терапии рака нелинейной акустикой [32]. Начальные условия
для уравнения (14) будут определять крутизну ударного фронта нелинейного
литотриптера, так как надо задать (k2)¢ в начальной точке в прямой волновой задаче. В обратной волновой задаче крутизна должна определяться в
зависимости от предела эластичности конкрементов и раковых клеток. Для
повышения эффективности электромагнитной терапии необходимо между облучаемой
клеткой и излучателем электромагнитных волн создать среду тяжелого азота с
концентрацией 15N, превышающей 10.95‰
или 0.365%. В экологически чистых регионах содержание
15N в атмосфере меньше 0.365%, что обуславливает выживаемость организмов, у
которых низкая концентрация 15N в клетках. В регионах, где в атмосфере содержание 15N больше 0.365%, 15N накапливается в клетке по сравнению с нормальным значением, равным 7.5%, а отклик организма начинается на значениях
концентрации, превышающих критическое значение, равное 10.95‰, но это уже
вызывает болезни и смерть. Возможно, к таким регионам надо отнести Коричневое
Азиатское облако.
ЛИТЕРАТУРА
1. Гинзбург В.Л. Нобелевская лекция // УФН. 2004. Т. 174. № 11. С. 1240-1255.
2.
Балеску Р.
Равновесная и неравновесная статистическая механика. Т. 1. М.: Мир, 1978. 406
с.
3.
Брагинский А.Я.
Неоднородные упорядоченные состояния и трансляционная природа калибровочной группы
в континуальной теории Ландау. I. Общее
рассмотрение // ЖЭТФ. 2007. Т. 132. Вып. 1(7). С. 40-44.
4.
Гуфан А.Ю.
Полносимметричный параметр порядка в феноменологической теории фазовых
переходов. Сегнетоэластики // ЖЭТФ. 2007. Т. 132. Вып. 1(7). С. 138-149.
5.
Иванов Д.Ю.
Феноменологическая модель критического поведения реальных систем // Докл. РАН.
2004. Т. 394. № 6. С. 757-760.
6.
Погорелов А.А., Суслов
И.М. Ренормгрупповые функции для двумерных фазовых переходов: к вопросу о
сингулярных вкладах // ЖЭТФ. 2007. Т. 132. Вып. 2(8). С. 406-416.
7.
Берри Р.С., Степанов
Б.М. Фазовые переходы и сопутствующие явления в простых системах связанных
атомов // УФН. 2005. Т. 175. № 4. С. 368-411.
8.
Коршунов С.Е. Фазовые
переходы в двумерных системах с непрерывным вырождением // Там же. 2006. Т. 176. № 3. С. 234-274.
9.
Смирнов Б.М. Кластеры и
фазовые переходы // Там же. 2007. Т. 177. № 4.
С. 369-373.
10. Gross D.J., Witten
E. Possible third-order phase
transition in the large-N lattice gauge theory // Phys. Rev. D. 1980. Vol. 21. P. 446-453.
11. Eisele T. On a
third-order phase transition // Communic. in Mathem. Phys. 1983. Vol.90. No 1.
P.125-159.
12. Azakov P. I.
One-plaquette (2+1)-model with arbitrary action // Theoretical and Mathematical Physics. 1985. Vol.62.
No.2. P. 222-235.
13. Cronström
C., Noga M. Third-order Phase
Transition and Superconductivity in Thin Films // Czechoslovak J. Phys.
2001. Vol. 51. No 2. P. 175-184.
14. Alimohammadi
M., Khorrami M. On the phase structure of two-dimensional generalized
Yang-Mills theories // Nucl. Phys. 2001. B597. P. 652-661.
15. Li L., Meurice Y. Is there a
third-order phase transition in quenched OCD? // Proceedings of Science XXIIIrd International Symposium on Lattice
Field Theory. 25-30 July 2005. Trinity College, Dublin, Ireland. P.
258/1-258/6.
16. Ландау Л.Д., Лифшиц Е.М. Статистическая физика. Ч. 1.
М.: Наука, 1995. 608 с.
17. Kondepudi D.K., Nelson, G.W.
Chiral Symmetry Breaking in Nonequilibrium Systems // Phys. Rev. Lett. 1983. Vol. 50. P. 1023-1026.
18. Kondepudi
D.K., Nelson G.W. Weak neutral
currents and the origin of biomolecular chirality // Nature. 1985. Vol. 314. P. 438-441.
19. Аветисов В.А., Гольданский В.И. Физические аспекты
нарушения зеркальной симметрии биоорганического мира // УФН. 1996. Т. 166. № 8. С. 573-591.
20. Островский В.Е., Кадышевич Е.А. Обобщенная гипотеза
происхождения простейших элементов живой материи, трансформации первичной
атмосферы и образования залежей гидрата метана // УФН.
2007. Т. 177. № 2. С. 183-206.
21. Bazarov I.P.,
Bondarenko V.V. On the impossibility of the third and higher order phase
transitions // J. Phys. Chem. (Russia). 1996. Vol. 70. N. 7. P. 1198-1200.
22. Тукембаев Ч.А. Значение ориентированного объема для
оптической активности и фазового перехода 3 рода // Математическая морфология.
2007. Т. 6. Вып. 4. http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
23. Тукембаев Ч.А. Фазовый переход при
образовании солитонов и трансформации замкнутой системы термодинамики в
открытую систему // Физико-химический
анализ многокомпонентных систем. 2007. Вып. V. http://kubstu.ru/fh/fams
24. Тукембаев Ч.А. Фазовый
переход и дилатансия в эксгаляции радона // Там же. 2008. Вып. VI. http://kubstu.ru/fh/fams
25. Тукембаев Ч.А., Васильев
И.А. Нелинейная эксгаляция радона как
фазовый переход // Радиоэколог. и смежные проблемы уранового пр-ва. Ч.V / Отв. ред. И.А. Васильев. Ин-т физики
НАН КР. Бишкек: Илим, 2008. С. 41-49.
26. Тукембаев Ч.А. Фазовый
переход в нелинейной эксгаляции радона // Известия Челябинского научного центра
РАН. 2008. Вып. 2(40) (в печати). http://www.csc.ac.ru/news/
27. Учайкин
В.В. Дробные производные в теории фазовых переходов // Обозрение приклад. и
промышл. математ. 2005. Т. 12. Вып. 2. С. 538-540.
28. Учайкин В.В. Автомодельная аномальная диффузия и
устойчивые законы // УФН. 2003. Т. 173. № 8. С. 847-876.
29. Руденко О.В. Гигантские нелинейности
структурно-неоднородных сред и основы методов нелинейной акустической диагностики
// УФН. 2006. Т. 176. № 1. С. 77-95.
30. Васильев А.Н., Бучельников В.Д., Такаги Т. и др.
Ферромагнетики с памятью формы // УФН. 2003. Т. 173. № 6. С. 577-608.
31. Гуляев Ю.В. Акустоэлектроника (исторический обзор) //
УФН. 2005. Т. 175. № 8. С. 887-895.
32. Руденко О.В. Нелинейные волны: некоторые
биомедицинские приложения // УФН. 2007. Т. 177. № 4. С. 374-383.
33. Синицын Н.И., Петросян В.И., Елкин В.А., Девятков
Н.Д., Гуляев Ю.В., Бецкий О.В. Особая роль системы «миллиметровые волны –
водная среда» в природе // Биомедицинская радиоэлектроника. 1999. № 1. С. 3-21.
34. Бецкий О.В., Кислов В.В., Лебедева Н.Н. Миллиметровые
волны и живые системы. М.: САЙНС-ПРЕСС, 2004. 272 с.
35. Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука,
1988. 736 с.
36. Ландау Л.Д., Лифшиц Е.М. Теория упругости. М.: Наука,
1987. 246 с.
37. Шамров Н.И. Переходное вынужденное комбинационное
рассеяние при полном фазовом согласовании // Математическое моделирование.
2002. Т. 14. № 6. С. 36-42.
38.
Бяков В.М., Степанов
С.В. К механизму первичного биологического действия ионизирующих излучений //
УФН. 2006. Т. 176. № 5. С. 487-506.
39. Патологическая физиология / Под ред. А.Д.
Адо и Л.М. Ишимовой. М.: Медицина, 1980. 520 с.
40. Liu A.J., Nagel S.R. Nonlinear dynamics:
Jamming is not just cool any more // Nature.
1998. Vol. 396. P.
21-22.
41. Cates M.E., Wittmer J.P.,
Bouchaud J.-P., Claudin P. Jamming,
force chains, and fragile matter // Phys. Rev. Lett. 1998. V. 81, P. 1841.
42. Trappe V., Prasad V.,
Cipelletti L., Segre P. N. , Weitz D. A. Jamming phase diagram for attractive particles
// Nature. 2001. Vol. 411. P. 772-775.
43. Olemskoi A.I., Khomenko A.V. Synergetic theory for a jamming transition in
traffic flow // Physical Rev. E. 2001. Vol. 63. No 036116. P. 1-4.
44. Caballero G., Kolb E., Lindner
A., Lanuza J., Clement E. Experimental investigation of granular dynamics close
to the jamming transition // Journal of Physics: Condensed Matter. 2005. V. 17.
N. 24. S. 2503-2516.
45. Cates M.E., Haw
M.D., Holmes
C.B. Dilatancy, jamming, and the physics of
granulation // J. Phys.: Condens. Matter. 2005. Vol. 17. N.24. P. S2517-S2531
46. Corwin E.I., Jaeger H.M., Nagel S.R. Structural signature of jamming in granular media // Nature. 2005. Vol. 435. P. 1075-1078.
47. Mezzenga R., Schurtenberger
P., Burbidge A., Michel M. Understanding foods as soft materials // Nature
materials. 2005. Vol. 4. P. 732-740.
48. Song Ch., Wang P., Potiguar
F., Makse H.A. Experimental and computational studies of jamming // Journal of
Physics: Condensed Matter. 2005. V. 17. N. 24. S. 2755-2765.
49. Зайцев В.Ю., Назаров В.Е., Турна В., Гусев В.Э.,
Костаньеде Б. Экспериментальное исследование нелинейных акустических эффектов в
зернистых средах // Акустический журнал. 2005. Т. 51. № 5. С. 633-644.
50. Зайцев В.Ю., Назаров В.Е., Таланов В.И.
"Неклассические" проявления микроструктурно-обусловленной
нелинейности: новые возможности для акустической диагностики // УФН. 2006. Т. 176. № 1. С. 97-102.
51. Мак-Мюррей У. Обмен веществ у человека. М.: Мир, 1980.
368 с.
52.
Валуйский П.П. Аспаргин
и лизин в питании телят. Фрунзе: Илим, 1983. 128 с.
53. Тукембаев Ч.А., Васильев И.А. Физика гипертермии и p–-терапии
рака // Известия вузов (Кыргызстан). 2003. № 3-4. С. 54-58.
54. Вебер А.В., Линк Д.В. Неолит Прибайкалья:
итоги и перспективы изучения // Археология,
этнография и антропология Евразии / СО РАН. 2001. № 1(5). С. 135-146.
55.
Ванин А.Ф. Оксид азота и
его обнаружение в биосистемах методом электронного парамагнитного резонанса //
УФН. 2000. Т. 170. № 4. С. 455-458.
56. Регигер С.А., Шадрина Н.Х. Математические модели транспорта оксида азота в
кровеносном сосуде // Биофизика. 2005. Т. 50. № 3. С. 515-536.
57. Серая И.П., Нарциссов Я.Р. Современные представления о
биологической роли оксида азота // Успехи современной биологии. 2002. Т. 122. №
3. С. 249-258.
58. Ульянова Н.А., Максимов Г.В., Чурин А.А., Рубин А.Б.
Исследование действия оксида азота (II) на вязкость мембран нервных клеток //
Биофизика. 2005. Т. 50. Вып. 2. С. 289-296.
59. Alderton W.K.,
Cooper C.E. Khowles R.G. Nitric oxide synthases: structure, function and
inhibition // Biochem. J. 2001. Vol. 357. P. 593-615.
60. Buerk D.G. Can we model nitric
oxide biotransport? A survey of mathematical models for a simple diatomic
molecule with surprisingly complex biological activities // Ann. Rev Biomed.
Eng. 2001. Vol. 3. P. 109-143.
61. Kelm M. Nitric oxide
metabolism and breakdown // Biochem. Biophys.
Acta. 1999. Vol. 1411. P. 273-289.
62. Nitric Oxide:
Principal and Actions / Ed. Lancaster J.R. San Diego etc.: Acad. Press, 1996.
355 p.
63. Wong A.Y.K., Klassen G.A. A
model of electrical activity and cytosolic calcium dynamics in vascular
endothelial cells in response to fluid shear stress // Ann. Biomed. Eng. 1995.
Vol. 23. P. 822-832.
64. Yang J., Clark J.W., Bryan
R.M., Robertson C. The myogenic response in isolated rat cerebrovascular arteries: smooth
muscle cell model // Med. Eng. Phys. 2003. Vol. 25. P. 691-709.
65. Yang J., Clark J.W., Bryan
R.M., Robertson C. The myogenic response in isolated rat cerebrovascular arteries: vessel
model
// In
the same place. P. 711-717.
66.
Таблицы
физических величин. Справочник / Под ред. И.К. Кикоина. М.: Атомиздат, 1976.
1008 с.
67. Siegwolf R.T.W., Matyssek R.,
Saurer M., Maurer S., Gunthardt-Goerg M.S., Schmutz P., Bucher J.B. Stable Isotope Analysis Reveals Differential Effects
of Soil Nitrogen and Nitrogen Dioxide on the Water Use Efficiency in Hybrid
Poplar Leaves // New Phytologist. 2001. V. 149. No 2. P. 233–246.
68. Trudell S.A., Rygiewicz P.T.,
Edmonds R.L. Patterns of nitrogen and carbon stable isotope ratios in
macrofungi, plants and soils in two old-growth conifer forests // New
Phytologist. 2004. V. 164. No 2. P. 317–335.
69. Тукембаев Ч.А., Васильев И.А. Физика гипертермии и p–-терапии
рака // Известия вузов
(Кыргызская Республика). 2003. № 3-4. С. 54-58.
70.
Еремин Е.Н.
Основы химической термодинамики. М.: Выс. шк., 1974. 341 с.
71. Некрасов Б.В. Основы общей химии. В 2-х т. М.: Химия
1973.
72. Тукембаев Ч.А. Гипертермия, митогенетическое излучение и зеркальные
изомеры в проблеме рака // Математическая
морфология. 2007. Т. 6. Вып. 3. http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
73. Тукембаев Ч.А. Влияние
критической концентрации тяжелого азота на обобщенную восприимчивость N2O в открытой
системе термодинамики // Физико-химический анализ многокомпонентных систем. 2007. Вып. V. http://kubstu.ru/fh/fams
74.
Левич В.Г.
Курс теоретической физики. В 2-х т. М.: Наука, 1969.
75. Надыкто Б.А. Об изотопном массовом сдвиге уровней
энергии гелиеподобных и литиеподобных ионов //
Докл. РАН. 1994. Т. 334. № 1. С. 41-43.
76. Махнев А.С. Об использовании
декартовых координат в молекулярной динамике // Физико-химическая кинетика в
газовой динамике. 2007. Т. 5. – http://www.chemphys.edu.ru/
77. Бреховских Л.М. Волны в слоистых средах. М.: Наука,
1973. 344 с.
78.
Тукембаев
Ч.А., Валуйский П.П., Васильев И.А., Пресняков К.А. Гамма-квантовые процессы в организме // Наука и новые
технологии (Кыргызская Республика). 2000. № 1. С. 202-214.
79. Тукембаев Ч.А. Роль боковой волны в электромагнитной терапии // Математическая морфология. 2007. Т.
6. Вып. 4. http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
80. Гинзбург В.Л. Излучение равномерно движущихся
источников (эффект Вавилова-Черенкова, переходное излучение и некоторые другие
явления) // УФН. 1996. T. 166. № 10. С. 1033-1042.
81. Корн Г., Корн Т. Справочник по математике. М.: Наука,
1984. 832 с.
82. Марчук Г.И. Методы расщепления. М.: Наука, 1988. 264
с.
83. Бахрах С.М., Глаголева Ю.П., Самигулин М.С., Фролов
В.Д., Яненко Н.Н., Янилкин Ю.В. Расчет газодинамических течений методом
концентраций // Докл. АН СССР. 1981. Т. 257. № 3. С. 566-569.
84. Бондаренко Ю.А., Янилкин Ю.В. Расчет термодинамических
параметров смешанных ячеек в газовой динамике // Математическое моделирование.
2002. Т. 14. № 6. С. 63-81.
85. Абакумов М.В., Мухин С.И., Попов Ю.П., Рогожкин Д.В.
Ударные волны разрежения в численных решениях задач газовой динамики // Там же.
2008. Т. 20. № 1. С. 48-60.
86. Тукембаев Ч.А. Обобщение схемы Роте или модификация
метода интегральных соотношений // Исследования по интегро-дифференциальным
уравнениям. 1992. Вып. 24. С. 256-261.
87. Тукембаев Ч.А. Метод исследования устойчивости
численного решения нелинейных задач математической физики // Там же. С. 261-
267.
88. Тукембаев Ч.А. Обобщение метода Римана – точное
решение консервативных уравнений гидродинамики. Бишкек: Илим, 1994. 92 с.
89.
Жуховицкий
Д.И. Поверхностное натяжение границы раздела пар-жидкость с конечной кривизной
// Коллоидный журнал. 2003. Т. 65. № 4. С. 480-494.
90. Birkhoff G. Numerical dynamics
// SIAM Rev. 1983. V. 25. No 1. P. 1-34.
91. Айтматов И.Т., Тажибаев К.Т. Явление скачкообразного
освобождения остаточных напряжений в горных породах // Диплом № 90 на научное
открытие РАЕН / Регистр № А-109 от 29.04.98 г.
92. Камке Э. Справочник по обыкновенным дифференциальным
уравнениям. М.: Наука, 1978. 576 с.
93. Малкин И.Г. Теория устойчивости движения. М.: УРСС,
2004. 432 с.
94. Тукембаев Ч.А. Интервальный критерий устойчивости //
Системы управления и обработки информации для подвижных объектов / Отв. ред.
В.М. Журавлев. Фрунзен. политехн. ин-т. Фрунзе, 1988. С. 45-47.
THE
STRUCTURAL NONLINEARITY in the mechanism of a cancer on the basis of isotopes
Tukembaev Ch. A.,
Svidenko V. N.
The analytical decision of a problem of structural nonlinearity of the high order is found provided that the set homogeneous density is three times differentiated function on dP. The decision is a theoretical substantiation of a multifrequency resonance and the isotope mechanism of a cancer in therapy by nonlinear acoustic and electromagnetic waves. It is shown, that jamming-transition is caused by a critical point for particles of solvent and the dissolved substance.
Keywords: nonlinear waves,
a multifrequency resonance, longitudinal and transverse Doppler Effect, therapy of a cancer, heavy nitrogen.
Авторы: Тукембаев Чоро Абдылдаевич,
старший преподаватель; Свиденко Владимир Николаевич, профессор, доктор
технических наук, лауреат премии "Золотая медаль Ататюрка".
Кафедра прикладной информатики
Кыргызский государственный университет строительства, транспорта и архитектуры
720020, Бишкек, ул. Малдыбаева, 34-б,
Кыргызстан,
тел.
+996(312) 549 223,
e-mail: choro@istc.kg
Department of applied computer science, Kyrgyz state
university of construction, transport and architecture,
34 “b”, Maldybaev Str., Bishkek, 720020, Kyrgyz Republic,
tel.: +996(312)
549 223,
e-mail: choro@istc.kg
Поступила в редакцию 14.06.2008.