Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 7. -
Вып. 3. - 2008. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-19-html/TITL-19.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-19-html/cont.htm
УДК 612.08:001.57
ОПТИМАЛЬНАЯ СТРУКТУРА МИКРОЦИРКУЛЯТОРНОЙ СЕТИ МЫШЦ
Ó 2008 г. Бухаров И. Б.
Предложена
математическая модель структуры микроциркуляторной сети мышц. Модель основана
на принципе минимальных энергетических затрат. Учитывается энергия, потребляемая
сердцем и костным мозгом, а также затраты энергии на перенос массы крови при
передвижении. Рассматривается микроциркуляторная сеть сердца, легких и скелетных
мышц. Определяется оптимальное число капилляров, ответвляющихся от одной
терминальной артериолы. Теоретические результаты сопоставляются с экспериментальными
данными для человека.
Ключевые слова:
микроциркуляторная сеть, принцип минимальных затрат.
Введение
При исследовании структуры системы кровообращения наибольшее распространение получил феноменологический подход, основанный на принципе оптимальности [6]. Выдвигается гипотеза, согласно которой в ходе эволюции видов структурная организация системы кровообращения оптимизировалась таким образом, чтобы минимизировать потребляемую ею энергию. Как и все принципы оптимальности, принцип минимальных энергетических затрат не может быть строго доказан. Его справедливость устанавливается естественно-научным путем, т.е. хорошим соответствием экспериментальных данных и теоретических результатов, следующих из этого принципа.
Принцип минимальных энергетических затрат
был успешно применен для определения структурных параметров не только отдельных
бифуркаций [18, 20, 22], но и всего сосудистого дерева органов и тканей [2, 5,
7, 12, 14].
Предсказываемый этими моделями общий
характер ветвления в сосудистой системе близок к наблюдаемому. Однако, имеются
заметные расхождения между предсказаниями модели и экспериментальными данными,
относящимся к малым артериям и капиллярам. Существенными особенностями этой
части системы кровообращения являются 1) центральная роль диффузии кислорода в
процессах капиллярно-тканевого обмена и 2) регуляция общего периферического
сопротивления сосудов, главным образом, в области малых артерий и артериол.
Целью статьи является применение принципа
минимальных энергетических затрат для определения структурных параметров
микроциркулярной сети мышц.
Целевая функция
Проблема математически формулируется как задача оптимизации с выбранной целевой функцией и ограничениями. Конкретная форма целевой функции зависит от особенностей рассматриваемой системы. Для артериальной системы, основной вклад в ее энергетику вносят энергетические затраты артерий, артериол и капилляров
(1)
где W – энергетические затраты артериальной системы в
единицу времени, 
– энергетические затраты артерий от аорты до терминальных артериол
в единицу времени, 
– энергетические затраты терминальных артериол в единицу времени, 
– энергетические затраты капилляров в единицу времени.
Величина 
представляет собой суммарные энергетические затраты сосудистых генераций
от аорты до терминальных артериол
, (2)
где 
– энергетические
затраты сосудов i-ой генерации в единицу времени, N – число генераций
в артериальной системе, i – номер генерации
(3)
где 
– кровоток, 
– гемодинамическое
сопротивление сосудов i-ой генерации, 
– среднее время жизни
эритроцитов, 
– объем тела, 
– объем крови в
сосудах i-ой генерации, 
– основной обмен, 
– концентрация
эритроцитов в крови, α – энергия
синтеза эритроцита, β –
видоспецифический коэффициент, 
– кпд сердца.
Первый член в (3) представляет собой
энергетические затраты сердца в единицу времени вследствие вязкой диссипации в
сосудах i-ой генерации, второй – «энергетическую ценность
крови» [18], которая включает энергетические затраты на генерацию эритроцитов и
перенос массы крови, находящейся в сосудах i-ой генерации.
Согласно формуле Пуазейля,
(4)
где 
– число ветвей в
сосудах i-ой генерации, 
– длина сосудов i-ой генерации,
– радиус сосудов i-ой
генерации, μ – вязкость крови
(5)
В оптимальном ветвящемся трубопроводе [7]
(6)
(7)
где 
– длина ветви нулевой
генерации, m – коэффициент ветвления (множитель, на который
возрастает число ветвей в каждой последующей генерации).
По аналогии с (3) можно написать для терминальных
артериол
(8)
где 
– гемодинамическое
сопротивление терминальных артериол, 
– энергетические
затраты терминальных артериол в оптимальном ветвящемся трубопроводе в единицу
времени, 
– длина терминальных
артериол в оптимальном ветвящемся трубопроводе, 
– длина терминальных
артериол
(9)
(10)
где 
– число терминальных
артериол, 
– радиус терминальных
артериол.
В оптимальном ветвящемся трубопроводе [7]
(11)
(12)
Типичная структура микроциркуляторной сети
мышц показана на рис. 1.
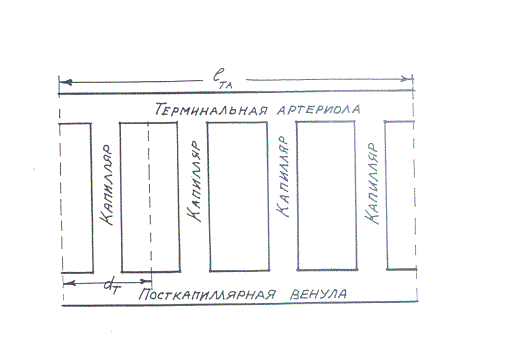
Рис. 1. Типичная структура микроциркуляторной сети мышц [21].
dT – диаметр кроговского тканевого цилиндра,
lTA – длина терминальных артериол
Терминальные артериолы связаны с посткапиллярными венулами параллельной сетью капилляров.
Как видно из рисунка,
(13)
где 
– диаметр кроговского тканевого цилиндра, k – число
капилляров, ответвляющихся от одной терминальной артериолы.
может быть выражен через объем V и площадь поверхности капилляров S органов и
тканей
(14)
(15)
где 
– число капилляров, 
– длина капилляров, 
– радиус капилляров.
Из (14) и (15) следует
(16)
По определению
(17)
Для капилляров можно написать аналогичным образом
(18)
где 
– гемодинамическое
сопротивление капилляров, 
– объем крови в
капиллярах
(19)
Ограничения
При поиске экстремума целевой функции (1)
учитывались следующие ограничения:
1)
объем органов и тканей V задан
V = const,
(21)
2) кислородное потребление органов и
тканей 
задано
(22)
или в эквивалентной форме
S = const
(23)
так как диффузионный поток кислорода из капиллярной
крови в окружающую ткань пропорционален площади поверхности капилляров S [15],
3)
кровоток в органах и
тканях 
задан
(24)
Оптимальные микроциркуляторные параметры
Целевая функция (1) с учетом ограничений (21), (23), (24) и (11-13, 17) принимает вид
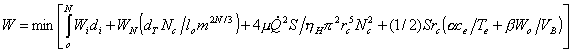(25)
Ввиду большого числа генераций N, в первом
члене (25) суммирование заменено интегрированием по i.
В рассматриваемом приближении имеются два
независимых структурных параметра Nc и N. Оптимальные величины этих параметров определяются из
системы уравнений
(26а)
(26б)
Второй член в (26б) может быть опущен, так
как в оптимальном ветвящемся трубопроводе энергетические затраты ветвей не
зависят от номера генерации: 
[7].
Решая (26а) и (26б) относительно Nc
и N, находим
(27)
[
], (28)
где 
Целевая функция W (25) имеет
абсолютный минимум в точке 
в физиологической
области изменения Nc и
N.
Зная 
и 
, можно найти оптимальное
число капилляров, ответвляющихся от одной терминальной артериолы kопт с
помощью (11) и (17).
Типичные значения параметров, входящих в
(3), (8) и (18), для человека: Te =
120 сут, VB = 70 л, Wo = 85 Вт, ce = 5·109 1/мл, α = 1,7·10-6 Дж, β = 0.7, 
= 0,22, μ = 3
спз [9-11, 16, 19].
Исходные данные для расчета приведены в
табл. 1.
Таблица 1
Базисные микроциркуляторные параметры для человека [3, 8, 13, 17]
|
Органы и ткани |
m |
lo (см) |
lc (мк) |
rc (мк) |
S (м2) |
V (л) |
|
|
Сердце |
2 |
1,5 |
500 |
3 |
10 |
0,3 |
0,2 |
|
Легкие |
3 |
12 |
700 |
4 |
60 |
0,5 |
5,5 |
|
Скелетные мышцы |
2 |
18 |
900 |
3 |
300 |
31,5 |
1,1 |
Результаты расчетов представлены в табл. 2.
Таблица 2
kопт в различных органах и тканях
|
Органы и ткани |
Сердце |
Легкие |
Скелетные мышцы |
|
Теория |
4 |
15 |
4 |
|
Эксперимент [1, 4, 21] |
3-6 |
12-18 |
3-5 |
Как видно из табл. 2, теоретические результаты
находятся в удовлетворительном соответствии с экспериментальными данными.
В (27) и (28) входят два безразмерных
параметра ψ1 и ψ2:
Nc ~ ψ1 и N ~ ln ψ2, что говорит об отсутствии аномальной чувствительности
решения к изменению этих параметров.
Заключение
Представленные результаты свидетельствуют
о применимости принципа минимальных энергетических затрат для определения
структурных параметров микроциркуляторной сети мышц.
Существование оптимального числа капилляров и сосудистых генераций в артериальной системе может быть объяснено конкуренцией двух факторов.
Для заданной площади поверхности капилляров, длина капилляров и, следовательно, их энергетические затраты снижаются с увеличением числа капилляров. С другой стороны, длина терминальных артериол и, следовательно, их энергетические затраты растут с увеличением числа капилляров.
Энергетические затраты артериального
дерева от аорты до терминальных артериол растут с увеличением числа генераций.
С другой стороны, длина терминальных артериол и, следовательно, их
энергетические затраты снижаются с увеличением числа генераций.
Заметим, что приведенные в табл. 2
значения kопт относятся к простейшей структуре микроциркуляторной
сети, наблюдаемой в сердце, легких и скелетных мышцах [21].
Структура микроциркуляторной сети в других
органах (желудок, печень, селезенка) более сложная [21] и требует специального
рассмотрения. В этом случае предложенная модель неприменима и должна быть модифицирована.
Автор благодарит проф. М.А. Ханина за
полезные дискуссии.
Литература
1.
Вейбель Э. Морфометрия легких человека. – Пер. с англ. – М.: Медицина,
1970. – 175 с.
2.
Григорян С.С., Гоциридзе Н.Ш. Об оптимальной организации органной
артериальной сети // Механика биологических сплошных сред / Под ред. С.С.
Григоряна, С.А. Регирера. – М.: Изд-во МГУ, 1986. – с. 119-124.
3.
Левтов В.А., Регирер С.А. Движение крови по артериям // Руководство по
физиологии. Физиология кровообращения. Физиология сосудистой системы / Под ред.
Б.И. Ткаченко, Г.С. Мазуркевича, А.И. Тюкавина и др. – Л.: Наука, Ленинградское
отд-ние. 1984. – с. 94-140.
4.
Маковецкий В.Д., Стебельский С.Е., Козлов В.А., Мишалов В.Д.
Морфологические механизмы регуляции кровотока в гемомикроциркуляторном русле
сердца человека в онтогенезе // Архив анат. гистол. и эмбриол. – 1989. – Т. 96,
№ 2. – с. 26-33.
5.
Мелькумянц А.М. Оптимальная структура артериальной сети скелетных мышц
// Бюллетень экспер. биол. мед. – 1978. – Т. 86, № 9. – с. 259-262.
6.
Розен Р. Принцип оптимальности в биологии. – Пер. с англ. – М.: Мир,
1969. – 215 с.
7.
Черноусько Ф.Л. Оптимальная структура ветвящихся трубопроводов // Прикл.
мат. мех. – 1977. – Т. 41, № 2. – с. 376-383.
8.
Шошенко К.А. Кровеносные капилляры. – Новосибирск: Наука, Сибирское
отд-ние, 1975. – 374 с.
9. Albritton E.C. Standard values in blood. –
Philadelphia-London: W.B. Saunders, 1953. – 199 p.
10.
Altman P.L., Dittmer D.S. Respiration and Circulation. – Bethesda: Federation
of American Societies for Experimental Biology, 1971. – 224 p.
11.
Bing R.J. Cardiac metabolism // Physiol. Rev. – 1965. – v. 45, № 2. – p.
171-214.
12. Cohn D. Optimal systems. I: The vascular system
// Bull. Math. Biophys. – 1954. – v. 16, № 1. – p. 59-74.
13.
Cumming G., Harding L.K., Horsfield K. etc. Morphological aspects of the
pulmonary circulation and of the air-ways // Fluid Dynamics of Blood Circulation
and Respiratory Flow. AGARD Conf. Proc. – 1970. – v. 65, sect 23. – p. 0-6.
14.
Kamiya A., Togawa T. Optimal branching structure of the vascular tree // Bull.
Math. Biophys. – 1972. – v. 34, № 4. – p. 431-438.
15.
Landis E.M., Pappenheimer J.R. Exchange of substances through the capillary
walls // Handbook of Physiology. Section 2. Circulation / Ed. by W.F. Hamilton,
P. Dow. – Washington, DC: American Physiological Society, 1963. – v. 2. – p.
961-1034.
16.
Margaria R.A., Cerretelli C., Aghemo P., Sassi G. The energy cost of running //
J. appl. Physiol. – 1963. – v. 18, № 2. – p. 367-370.
17.
McAlpine W.A. Heart and Coronary Arteries. – Springer-Verlag, 1975. – 224 p.
18.
Murray C.D. The physiological principle of minimum work // Proc. Natl. Acad.
Sci (USA). – 1926. – v. 12, № 3. – p. 207-214.
19.
Rubner M. Elementary Zusammensetzung, Verbrennungswarme und Verbrauch der organischen
Nahrungsstoffe // Handbuch der Normalen und Pathologischen Physiologie / Hrsg.
von G.V. Bergmann, G. Embden, A. Ellinger. – Berlin: Springer-Verlag, 1928. –
Bd. 5. – s. 17-27.
20.
Uylings H.B.M. Optimization of diameters and bifurcation angles in lungs and
vascular tree structures // Bull. Math. Biol. – 1977. – v. 39, № 5. – p.
509-520.
21.
Wiedeman M.P., Tuma R.F., Mayrovitz A.N. An introduction to microcirculation. –
New York: Academic Press, 1981. – 226 p.
22.
Zamir M. Optimality principles in arterial branching // J. Theor. Biol. – 1976. – v. 62, №
1. – p. 227-251.
OPTIMAL STRUCTURE OF
THE MICROCIRCULATORY NETWORK
IN MUSCLES
Bukharov I. B.
A mathematical
model of the structure of the microcirculatory network in muscles is proposed.
The model is based on the principle of minimum energy expenditure. The energy
expenditure of the heart, bone marrow and the energy expended in blood carrying
are taken into account. The microcirculatory network in the heart, lung and
skeletal muscles is considered. The optimal number of capillaries arising from
one terminal arteriole is determined. Theoretical results are compared with
experimental data for man.
Key words: microcirculatory
network, principle of minimum energy expenditure
Центр теоретических проблем
физико-химической фармакологии РАН,
119991 г. Москва, Россия
Centre for Theoretical
Problems of Physico-Chemical Pharmacology, Russian Academy of Sciences, Moscow
119991, Russia
Поступила в редакцию
11.09.2008