Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 7. -

Вып. 4. - 2008. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ

http://www.smolensk.ru/user/sgma/MMORPH/N-20-html/TITL-20.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-20-html/cont.htm

УДК530.1+577.391

К вопросу об эффекте рассасывания метастаз на ударном фронте нелинейного литотриптера

Ó 2008 г. Тукембаев Ч. А.

(tukembaev.doc)

В работе исследован эффект рассасывания метастаз при их стимулировании мощным ударным фронтом волны ультразвука. Частицы опухоли рассматриваются как отрицательные элементы объема или элементы левой среды. Доказано, что исчезновение метастаз обусловлено не ударным фронтом, а волной разрежения, которая вызывает фазовый переход 1 рода. Для элементов левой среды требуется резонанс, который выбрасывает элементы левой среды из жидкой фазы в газовую фазу. Выведена формула, объясняющая осмос молекул сквозь биологическую мембрану. Формула позволяет изучать осмос как сверхтекучесть или как квантовый эффект.

Ключевые слова: левая среда, рак, ультразвук, нелинейная волна, фазовый переход, осмос.

Ультразвук в лечении рака получил признание и, особенно, эффективен с помощью нелинейных литотриптеров. Эффективность зависит от крутизны ударного фронта импульса, сфокусированного на опухоль, что приводит к ее разогреву на несколько десятков градусов, т.е. разрушение опухолевых клеток основано на гипертермии. Механизмами разрушения могут быть большое отрицательное напряжение из-за отражения импульса, сдвиговое напряжение, усталостные повреждения, кавитационная эрозия из-за больших градиентов давления p и гигантских ускорений ~10⁹ g на ударном фронте. Пиковое положительное давление на ударном фронте равно 10⁷ – 10⁸ Па, а на волне разрежения пиковое отрицательное давление на порядок меньше [1, c. 380]. Крутизна ударного фронта положена в объяснение эффекта рассасывания метастаз [1, c. 382] и теоретически основана на нелинейных модулях упругости Ландау 3 порядка, как структурная нелинейность [2].

Структурная нелинейность определяется нелинейной длиной волны l_n. Нелинейная длина волны, в свою очередь, определяется длиной l волны, нелинейным параметром e@10²–10³, оценка которого требует измерений, 2 и 3 гармониками колебаний и кубом скорости звука - v³ для связи с уравнениями римановых волн, Бюргерса и Вольтерра в средах с гистерезисом для запоминания свойств среды [2]. Однако гистерезис надо связывать с многозначной функцией, которая не рассматривается в [2], так как основана на нелинейных модулях упругости Ландау. Многозначная функция появляется при изучении сжимаемости, как функции, обратной упругости. Изотермы Ван-дер-Ваальса p(V) надо представить графиком V(p). В [3-4] получены линейные модули сжимаемости 3 порядка (ЛМС) для описания упруго-сжимаемых сред, левых сред и зеркальных изомеров, как части элементов левой среды. ЛМС выведены в точке перегиба (вблизи критической точки) с учетом левых элементов объема (-dV), что позволило изучать левые среды с помощью обыкновенных дифференциальных уравнений.

Отрицательное давление относится к метастабильному состоянию, где на линии особых точек ACD (см. рис. 1) и в ограниченной ею области спинодального разрыва характер особенности неизвестен [5, c. 319]. Физический смысл комплексного волнового числа определен, например, для обобщенной восприимчивости [5, c. 456], второй вязкости [6, c. 425, 438] и приобретает особый интерес в левых средах [7] и зеркальных изомерах (Пастер) [8]. Идея Kondepudi D.K., Nelson G.W. о накоплении хирального избытка в критической точке не выдержала критики (см. [8, c. 889]), но она стала плодотворной в проблеме рака [9]. В настоящей работе, так как частица рака не идентифицирована, мы изучим ее как элемент объема левой среды или как отрицательный элемент объема [10].

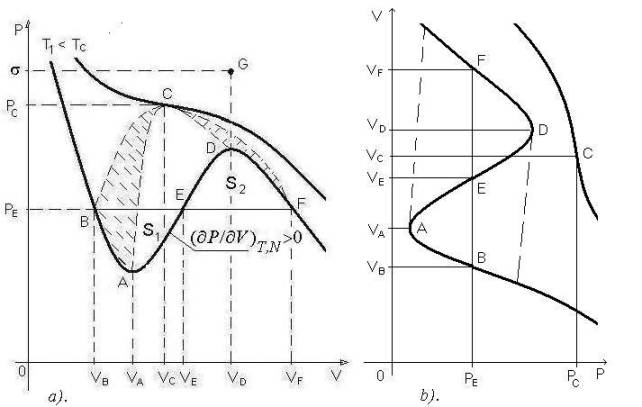
Рис. 1. Изотермы Ван-дер-Ваальса (а) и обратные ей изотермы (б).

В [1, 2] не предполагается существование -dV и критической точки, значения отрицательного давления p<0 на волне разрежения рассматриваются как акустическое давление только для положительных элементов объема +dV. Однако элемент объема легче разделить на 2 частицы при растяжении, а не сжатии [3, 4, 10], поэтому эффект рассасывания метастаз [1, c. 382] надо изучить на волне разрежения с учетом фазового перехода. Возникает вопрос: принадлежит ли частица рака левой среде, как -dV, и испытывает ли она фазовый переход на волне разрежения? В этой связи надо математически обосновать задачу. В отличие от работ, представленных в обзорах [1, 2] нам уже ранее было известно [9-13], что зеркальные изомеры и частицы рака надо исследовать в критической точке закиси азота N₂O совместно с оксидом азота ¹⁵NO и изотопом азота ¹⁵N, как веществом, являющимся благоприятной средой для развития рака.

Некорректность в определении l_n, а тем самым структурной нелинейности, допущенная в работе [2], по сути, есть эпицикл, наращиваемый на эпицикл. Это произошло, видимо, из-за попытки выразить нелинейную длину волны, как v³, и связать ее с боковой волной [6]. В ЛМС k²=w²/v² определяется через v²=¶p/¶r. Плотность среды r=r₀+r¢ задана суммой однородной r₀=const и неоднородной r¢, w=(s/m)^1/2 - частота колебаний, s - упругость по Гуку, m - масса. Поэтому из фазовой скорости v=w(t)/k(t), где t – параметр, напрямую следует групповая скорость u=dw/dk, что принципиально невозможно для нелинейной длины волны, поскольку классическая длина волны l пропорциональна скорости звука. Принцип суперпозиции для нелинейных волн не выполним, поэтому необходимо еще обосновать существование обратной функции для волнового числа, так как k=2pl^-1.

Наряду с ЛМС рассмотрим уравнение колебаний супергетеродина

(1)

b=1, AB - const, изученное A. Erdelyi [14, c. 383] для электромагнитных параметров, заданных в f. Так как механическим свойствам среды отвечает fºk² (будет показано далее), то только волновое число связывает электромагнитные параметры с механическими свойствами среды и, в том числе, упругие и электромагнитные волны. ЛМС 3 порядка можно свести в уравнение (1), если в силу закона сохранения кинетическая энергия элемента объема E=r₀v²/2=A – const, r – трижды, f – дважды дифференцируемая функция, а f²=±3B/2 – const, где знаки учитывает бифуркацию на зеркальные частицы, т.е. на левые и правые элементы объема.

Цель настоящей работы – доказательство того, что эффект рассасывания метастаз возникает на волне разрежения и его физической сутью является фазовый переход 1 рода.

Умножив сжимаемость c=-V₀^-1dV/dp на s, имеем sc=-w²rdV/dp. Объем V является многозначной функцией p. Петлю гистерезиса получаем, если нанесем

2 прямые линии (см. рис.) на график V(p). Эти линии проходят через точки A и D кривой V(p), что позволяет изучать среды с гистерезисом Вольтерра в рамках ЛМС. Считая j=sc, дифференцируем 3 раза левую и правую части выражения j=-w²rdV/dp:

(2)

(3)

(4)

где k²=w²(¶r/¶p)=w²/v², (k²)¢=w²(¶²r/¶p²), (k²)²=w²(¶³r/¶p³). В однородной среде плотность не зависит от r¢, поэтому a=w²r₀. Корень из k² дает пару параллельных векторов: k и –k, по абсолютной величине равных k.

Положим w=const, так как частота является фиксированным показанием прибора измерений. Тогда, дифференцируя k²=w²/v², получим

Поскольку (k²)¢=-2w²v^-3v¢, то это и есть связь с римановой волной: v³ получено дифференцированием, а не наложением l_n на l, как это сделано в [2]. Для (k²)²: 2k²v²/v-6k²(v¢/v)²<0, если v²<3v(ln v)¢²; 2k²v²/v-6k²(v¢/v)²>0, если v²>3v(ln v)¢². Поэтому инверсии знака (k²)² отвечает бифуркация на зеркальные частицы.

Лемма. Элемент объема dVÎR реальной среды, как правый элемент объема dV=+dV, но как левый элемент объема dV=-dV.

ДОКАЗАТЕЛЬСТВО. Усилим лемму внесением знаков под радикал. Так как dV=(±g)^1/2dx, x=(x₁, x₂, x₃) – криволинейные координаты, то ±dV²=dx², где квадрат якобиана g=±1. Знак "-" перед dV² отвечает мнимому элементу объема. Тогда элементы объема ±dV для правой среды берем со знаком "+", но для левой среды – со знаком "-", по определению. Лемма доказана.

Пока изотоп ¹⁵N не получил общего признания, как частица рака, будем считать ¹⁵N и его химические соединения элементами объема левой среды. В таком случае, если, согласно построению зеркальных изомеров [8], взять одинаковые атомы, и они совпадают с правой системой координат, система векторов x₁, x₂, x₃ образует правый элемент объема. Когда один из атомов замещен на атом с большой массой, то угол между двумя векторам x₁, x₂ будет тупым углом. Кратчайшим поворотом, теперь, будет обход по часовой стрелке. Следовательно, смешанное произведение, а им определяется объем через вычисление определителя, будет иметь отрицательный знак, так как косинус между векторам x₁, x₂ – это отрицательная величина. Такой элемент объема относим к левым или отрицательным элементам объема, согласно знаку.

ТЕОРЕМА 1. Пусть k²=w²(¶r/¶p), (k²)¢=w²(¶²r/¶p²), (k²)²=w²(¶³r/¶p³). Тогда в силу леммы "(+dV): k²>0, (k²)¢>0, (k²)²>0, но "(-dV): k²<0, (k²)¢>0, (k²)²<0.

ДОКАЗАТЕЛЬСТВО. Поскольку r¢=dm/dV, то путем подстановки +dV в k²=w²(¶r/¶p), (k²)¢=w²(¶²r/¶p²), (k²)²=w²(¶³r/¶p³) получаем k²>0, (k²)¢>0, (k²)²>0. Затем "(-dV) имеем: k²<0, (k²)¢>0, (k²)²<0. Итак, инверсия (k²)² зависит от знака ±dV, так как w и m > 0. Теорема доказана.

СЛЕДСТВИЕ 1. В левой среде фазовая v=w(t)/k(t)>0 и групповая u=dw/dk<0 скорости направлены друг против друга (v¯u), по определению [7, c. 440]. Производная (k²)¢=-2w²v^-3v¢ соответствует заднему фронту импульса – волне разрежения, где v¢>0. Для переднего фронта v¢<0, поэтому (k²)¢=2w²v^-3v¢. Эффект Доплера, теперь, зависит от римановой волны – v³ и групповой скорости v¢ºu=dw/dk. В силу теоремы 1 "(-dV) левые среды существуют не только в оптических средах [7], но и в механических средах.

Относительно вертикальной координаты z

где dv/dz – градиент скорости в касательном напряжении t=±mdv/dz, m - вязкость. Для слоистого движения dv/dz равно скорости сдвиговой деформации. Растяжение элемента объема ограничено его пределом прочности, после чего dV делится на 2 сферических элемента объема, но это зависит от производной (k²)². При бесконечном растяжении, помимо сдвига, для деления элемента объема пополам требуется приложить кручение, а это, вновь, зависит от (k²)². В гипертермии рака бесконечное растяжение возникает при критической температуре N₂O, равной 38.75 °C [9-13], которая больше порога гипертермии рака, установленного Европейским обществом иммунодефицита, на 0.25 °C.

Теорема 2. Пусть r₀v²/2=A – const, r – трижды дифференцируемая функция, (k²)²=±3B/2 – const. Тогда в точке перегиба система (2)-(4) "(-dV) описывается уравнением колебаний (1).

Доказательство. Подставим в систему (2)-(4) d⁴V/dp⁴=d²V/dp²=0 и получим в точке перегиба линейное (поэтому ЛМС) уравнение 3 порядка

(5)

Подстановка j¢=y, b=a/3 и f=k² в уравнение (5) дает уравнение 2 порядка

Поскольку "(-dV): f<0, f¢>0 и f²<0, то уравнение примет вид

(6)

Знак f²<0 уже учтен, а потому

и получим уравнение

Это уравнение описывает колебания "(k²)²<0, если AB<(k²)¢-k⁴/4b. Из условия, что f²º(k²)²=3B/2, меняем знак AB. Теперь на AB нет ограничения, поэтому получаем уравнение колебаний (1). Теорема доказана.

Таким образом, колебания зависят от знака (k²)². Как r связана с p, когда (k²)²=0? В этом случае w=0, так как r и m не равны нулю.

ТЕОРЕМА 3. Если (k²)²=0, то "(±dV) в пределах членов 3 порядка малости

(7)

ДОКАЗАТЕЛЬСТВО. Приравняв 2k²v²/v-6k²(v¢/v)² нулю, имеем уравнение

решение которого "v>0 имеет вид: v=|C₁p+C₀|^–1/2, cм. пример 6.125 в [14]. Однако v²=¶p/¶r, поэтому ¶r/¶p=|C₁p+C₀|, dr=|C₁p+C₀|dp. Тогда, соответственно v>0 и v<0, получаем 2 квадратных уравнения и их решения:

Они аналогичны решению для точек инверсии эффекта Джоуля–Томсона, следуя опытным данным которого, давление p<0, как нижняя точка инверсии, должно находиться в жидкости, а это отвечает отрицательному давлению в метастабильном состоянии. Корни p_1,2 лежат в области больших давлений, а точки инверсии в области малых давлений зависят от D=C₀²–2C₁(r+C₂)>0 корней p_3,4. А так как корни p_3,4 не комплексные величины, то

Поскольку r=r₀±dr+dr²±dr³>0, то получаем неравенство (7). Теорема доказана.

Начальные и краевые условия определяются константами C₀, C₁ и C₂, поэтому на них следует наложить ограничение, согласно неравенству (6), и если оно выполняется, то получаем уравнение колебаний (1), в котором AB=0. Корни p_1,2, p_3,4 дают отрицательные значения давления. Физическая суть комплексного значения p, когда D=C₀²–2C₁(r+C₂)<0, рассмотрена в работе [4] для объяснения прозрачных фантомов в волоконно-оптических линиях связи и в нелинейной диагностике рака [2, c. 92]. При этом надо всегда принимать во внимание, что элемент объема – это собственный параметр, в давление является внешним воздействием. Если элемент объема колеблется, например, пузырек газа в жидкой фазе, то периодическое решение, как собственная частота, относится к колебаниям элемента объема, а давление будет внешним периодическим воздействием. Параметры воздействия еще надо подобрать так, чтобы они совпали с собственной частотой элемента объема, и возник резонанс. Тогда пузырек газа из жидкой фазы будет выталкиваться в газовую фазу, т.е. будет совершаться фазовый переход, причем поведение элементов объема зависит знака элемента объема. Фактически это означает, что молекулы тяжелого азота ¹⁵N перейдут в газовую фазу, т.е. покинут клетку.

ТЕОРЕМА 4. Пусть выполнены условия теоремы 3 "(-dV) и DV=const. Тогда

(8)

ДОКАЗАТЕЛЬСТВО. Неравенство (8) получаем заменой r₀=m₀/V₀ и дифференциалов на приращения в неравенстве (7). Фазового перехода 1 рода нет, так как DV=const, поэтому члены Dm и D³m, обуславливают "сокращение" массы так, что частица с массой m₀ "проскальзывает" под определяемый неравенством (8) барьер и приобретает сверхтекучесть. В нашем случае сверхтекучестью обусловлено проникновение частицы сквозь мембрану. Это обусловлено тем, что производная dm/dV, аналогична u=dw/dk. Групповая скорость может превышать фазовую скорость, а в левой среде v¯u. Параметром в dm/dV является число частиц. Теорема доказана.

СЛЕДСТВИЕ 2. Для левых сред с u<0 выбор отрицательной массы не целесообразен [15, c. 142], поэтому получаем отрицательный элемент объема.

Рассмотрим поведение системы (2-4) "(+dV), когда k²>0, (k²)¢<0, (k²)²>0, и будем руководствоваться признаком левой среды v¯u.

ТЕОРЕМА 5. Пусть v>0, "(+dV): f>0, f¢<0, f²>0 и

(9)

Тогда в точке перегиба системы (2-4) "(-dV) имеем фазовый переход.

ДОКАЗАТЕЛЬСТВО. Уравнение (6) "(+dV): f>0, f¢<0 и f²>0 имеет вид

поскольку bf^-1f²=AB>0. Уравнение неустойчивое, так как f=w²/v²>0, поэтому колебаний не может быть, а потому рассмотрим одиночный импульс.

На ударном фронте импульса v¢ºu<0 и в этом случае условия теоремы не соблюдены, поскольку f¢>0. Однако, так как v¯u, то

Уравнение содержит особенность типа седло. На взаимодействие с элементом левой среды указывает v¯u. На заднем фронте условия теоремы выполнены в силу того, что v¢ºu>0, но v и u одинакового знака, поэтому получаем уравнение

корни которого

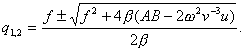
Если выполнено ограничение (9), то это особенность типа седло.

Колебания неограниченно растут, если

Тогда u должно быть больше v⁷, а это уже релятивистская область, причем требуется, чтобы u<с – скорости света. В нормальных условиях параметры импульса удовлетворяют неравенству (9), а это возможно, когда u<0, а, значит, v¯u. Следовательно, и передний, и задний фронты взаимодействуют с левым элементом объема. Поскольку y=sc¢, то неограниченный рост или скачок c¢, т.е. производной сжимаемости c, означает фазовый переход. Теорема доказана.

Таким образом, до настоящей работы температура, давление и масса были отрицательными величинами, среди которых только отрицательный или левый элемент объема имеет обоснование левой системой координат, когда один из атомов в правой системе координат замещен атомом с большой массой. Теорема 4 является теоретической базой проникновения молекул сквозь биологическую мембрану на основе квантового эффекта. При постоянной массе молекулы переменной величиной может быть только элемент объема. Поэтому вблизи критической точки растет -dV, что обуславливает сверхтекучесть, но рост ограничен фазовым переходом 1 рода. В силу теоремы 5, утверждение о том, что для рассасывания метастаз [1] надо наращивать крутизну ударного фронта, неверное. На ударном фронте наблюдается только взаимодействие переднего фронта с левым элементом объема. Эффект рассасывания метастаз – это фазовый переход, и он возникает на волне разрежения "(-dV), поскольку "(-dV) p<0. Именно волна разрежения, так как по данным [10] она обусловлена пиком отрицательного давления, вызывает растяжение левого или зеркального элемента объема и, в итоге, фазовый переход. Это означает, что надо направить ресурсы не на формирование все более крутых передних фронтов импульса. Требуется искать пути обрезания задних фронтов, чтобы усилить действие волны разрежения на метастазы.

ЛИТЕРАТУРА

1. Руденко О.В. Нелинейные волны: некоторые биомедицинские приложения // УФН. 2007. Т. 177. № 4. С. 374-383.

2. Руденко О.В. Гигантские нелинейности структурно-неоднородных сред и основы методов нелинейной акустической диагностики // УФН. 2006. Т. 176. № 1. С. 77-95.

3. Тукембаев Ч.А., Свиденко В.Н. Метод малого параметра в проблеме фазовых переходов // Исследования по интегро-дифференциальным уравнениям / Ин-т математики НАН КР. 2008. Вып. 38. (в печати).

4. Тукембаев Ч.А. Линейные модули сжимаемости 3 порядка в кроссмодуляции // Там же. Вып. 39. (в печати).

5. Ландау Л.Д., Лифщиц Е.М. Статистическая физика. М.: Наука, 1964. 568 с.

6. Ландау Л.Д., Лифщиц Е.М. Гидродинамика. М.: Наука, 1988. 736 с.

7. Блиох К.Ю., Блиох Ю.П. Что такое левые среды и чем они интересны? // УФН. 2004. Т. 174. № 4. С. 439-447.

8. Аветисов В.А., Гольданский В.И. Физические аспекты нарушения зеркальной симметрии биоорганического мира // УФН. 1996. Т. 166. № 8. С. 573-591.

9. Тукембаев Ч.А., Васильев И.А. Физика гипертермии и p^–-терапии рака // Известия вузов Кыргызской Республики. 2003. № 3-4. С. 54-58.

10. Тукембаев Ч.А. Значение ориентированного объема для оптической активности и фазовых переходов 3 рода // Математическая морфология / Математ. и медико-биолог. журнал / Смоленская гос. медицин. академия. 2007. Т. 6. Вып. 4. http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

11. Тукембаев Ч.А. Гипертермия, митогенетическое излучение и зеркальные изомеры в проблеме рака // Там же. Вып. 3. http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

12. Тукембаев Ч.А. Влияние критической концентрации тяжелого азота на обобщенную восприимчивость N₂O в открытой системе термодинамики // Физико-химический анализ многокомпонентных систем / Кубанский государственный технологический университет. 2007. Вып. V. http://kubstu.ru/fh/fams

13. Тукембаев Ч.А. Фазовый переход при образовании солитонов и трансформации замкнутой системы термодинамики в открытую систему // Там же. http://kubstu.ru/fh/fams

14. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М.: Наука, 1976. 576 с.

15. Гинзбург В.Л. Теоретическая физика и астрофизика. Дополнительные главы. М.: Наука, 1981. 504 с.

To a question on effect of eradication a metastasis on shock front of nonlinear lithitriptor

Tukembaev Ch.A.

In work the effect of eradication a metastasis is researched at their excitation by powerful shock front of a wave of ultrasound. Particles of a tumour are presented as negative elements of volume or as elements of the left-handed medium (LHM). It is proved; eradication of metastasis is caused not by shock front. The eradication is caused by a wave of underpressure which, in turn, causes first-order phase transition. For elements of LHM the resonance which throws out elements of LHM from a liquid phase in a gas phase. The formula is deduced; which explains osmose of molecules through a biological membrane. The formula allows to study osmose as superfluidity or as quantum effect.

Key words: left-handed medium, cancer, ultrasound, nonlinear wave, phase transition, osmose.

Pages – 13, figures – 1, bibliography – 15 references.

Department of applied computer science,

Kyrgyz state university of construction, transport and architecture,

34 “b”, Maldybaev Str., Bishkek, 720020, Kyrgyzstan,

tel.: +996(312) 549 223,

e-mail: choro@istc.kg

Автор: Тукембаев Чоро Абдылдаевич.

Кыргызский государственный университет строительства, транспорта и архитектуры,

кафедра прикладной информатики, старший преподаватель,

720020, Бишкек, ул. Малдыбаева, 34-б, Кыргызстан,

тел. +996(312) 549 223, e-mail: choro@istc.kg

Кафедра прикладной информатики

Кыргызский государственный университет строительства, транспорта и архитектуры.

Бишкек, Кыргызстан

Поступила в редакцию 24.11.2008.