Математическая морфология.
Электронный математический и медико-биологический
журнал. - Т. 8. -
Вып. 1. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/TITL-21.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/cont.htm
УДК 532.5+591.173+591.174
УСЛОВИЕ УДЕРЖАНИЯ ОПОРЫ В РУКЕ
Ó 2008 г. Покатилов А.Е., Загревский В.И., Попов В.Н.,
Максимова М.В.,
Чухмакова С.А.
Для многих спортивных дисциплин удержание контакта
со снарядом является определяющим фактором, влияющим в конечном итоге на оценку
упражнения и саму возможность его выполнения. Рассмотрены условия удержания
круглой опоры, типа перекладины в спортивной гимнастике. Предложено несколько
видов моделей. Проанализировано понятие круга трения и методов расчета
параметров фрикционного контакта с учетом значительной величины коэффициента
трения на контактной поверхности.
Особенностью
опорной кинематической пары «снаряд – рука» является наличие мягких биологических тканей, деформирующихся во время
движения спортсмена. Происходит смещение опорных реакций и сил трения по
аналогии с подшипниками скольжения технических устройств. Этот фактор оказывает
влияние на модели трения.
В общем виде описано влияние анатомии кисти на
распределение контактного давления между пальцами руки и ладонью. Показано смещение давления во время движения
человека для каждого пальца руки.
Ключевые слова: спортивная
гимнастика, биомеханика.
Введение
Трение в контакте человека со спортивным снарядом
играет важнейшую роль при целенаправленном движении. На практике для его
увеличения используют специальные присыпки и накладки для рук. При
теоретическом исследовании в уравнениях движения спортсмена, записанных
относительно опоры, появляются моменты сил трения. В ряде работ приведены
расчетные модели трения, которые можно использовать для анализа закономерностей
фрикционного контакта человека и снаряда во время движения [1-3].
Рассматривая трение руки о спортивный снаряд, в
качестве аналога можно использовать методики расчета подшипников скольжения с
поправкой на анатомию человека и свойства биологических тканей, участвующих в
контакте. В работе [4] рассмотрено трение во вращательной кинематической паре в
условиях сухого трения. Принятые допущения по трению в паре «рука – опора»
несколько отличаются от допущений, используемых при анализе трения в теории
механизмов и машин, но сам подход является весьма полезным и его можно взять на
вооружение.
Отметим, что еще одним аспектом задачи исследования
трения при контакте руки с опорой является вопрос сохранения контакта во время
спортивного упражнения. Данный момент актуален, как по причине особой
конструкции кисти руки (ее анатомии), так и по причине силовых возможностей
мышц, обеспечивающих хват.
Следующей особенностью фрикционного контакта
является большое значение коэффициента трения, что существенно меняет подходы к
расчетным моделям трения. Ряд допущений, используемых при расчете шарниров в
технике, нельзя применить для цилиндрических шарниров, моделирующих
кинематические пары биомеханической системы.
Ну и, конечно же, ткань руки не является абсолютно
твердым телом, и даже просто твердым, а проявляет вязко-упругие свойства [5].
Это влияет на распределение давлений на контактной поверхности, и как
следствие, на силы трения.
Условие удержания опоры в руке
Рассмотрим
случай сжатия опоры, когда силы, действующие с противоположных сторон, не лежат
на одной линии, или эта линия не проходит через центр поперечного сечения. Для
анализа возьмем два варианта:
1.
Внешняя
сила нормальна к поверхности контакта.
2.
Внешняя
сила параллельна горизонтальной оси координат (ординате OY).
|
|
|
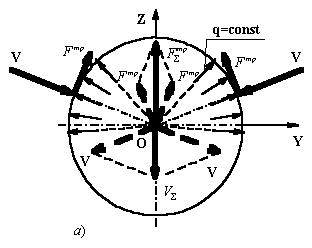
Рис. 1.
Частные случаи сжатия опоры рукой: а) – сжимающие силы нормальны опорной поверхности; б) – сжимающие силы
направлены по общей хорде |
Вариант действия
нормальной силы V показан на рисунке 1, а. Таких сил две. Приведем их к
центру O поперечного сечения. Сумма
сил дает результирующую силу ![]() , направленную вниз. Соответственно суммарная сила трения
, направленную вниз. Соответственно суммарная сила трения ![]() действует в
противоположную сторону. Она также приведена к центру O.
действует в
противоположную сторону. Она также приведена к центру O.
Понятно, что
условием отсутствия движения, т.е.
условием удержание опоры в захвате будет следующее соотношение между
внешней силой и силой трения
|
|
(1) |
Для удержания опоры
в руке необходимо, чтобы суммарная сила трения, возникающая на контактной
поверхности, превышала, или, в крайнем случае, была равна суммарной сжимающей силе.
На рисунке 1, б показан второй вариант, когда силы
лежат на одной линии, но эта линия является
хордой, а не диаметром круга. В случае шероховатой поверхности силу V можно представить как сумму
нормальной ![]() и касательной
и касательной ![]() сил составляющих
полную силу. Сила, находящаяся в касательной плоскости, является силой трения скольжения [4].
сил составляющих
полную силу. Сила, находящаяся в касательной плоскости, является силой трения скольжения [4].
Приведем силы к
центру O поперечного сечения. Сумма
нормальных сил дает результирующую силу ![]() , направленную вниз. Соответственно суммарная сила трения
, направленную вниз. Соответственно суммарная сила трения ![]() действует в противоположную
сторону. Она также приведена к центру O на рисунке 1, б. Способы
приведения сил к указанному центру влияния на результат не оказывают.
действует в противоположную
сторону. Она также приведена к центру O на рисунке 1, б. Способы
приведения сил к указанному центру влияния на результат не оказывают.
Условием
отсутствия движения будет отношение
|
|
(2) |
Сюда входит не вся
сжимающая сила, а только ее нормальная составляющая.
Круг трения
Рассмотрим
понятие круга трения применительно к задачам биомеханики. Анализ выполним для
спортсмена, находящегося в движении. Примем допущение об отсутствии смещения реакции
в контакте человека с опорой. Так как сумма удельного давления по всей площади
контакта при всестороннем охвате рукой опоры равна нулю (угол охвата опоры
равен ![]() ) по причине равномерного распределения в зоне контакта, то
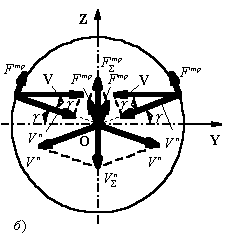
рассмотрим только случай, когда нормальная реакция N в опорном шарнире проходит через центр опоры, круглой в
поперечном сечении (рис. 2). В случае движения к руке приложен движущий момент Mдв. При этом возникают силы
трения F и момент трения MF. Сумма нормальной реакции N и силы трения F дают полную реакцию R,
которая отклонена от нормальной реакции на угол трения
) по причине равномерного распределения в зоне контакта, то
рассмотрим только случай, когда нормальная реакция N в опорном шарнире проходит через центр опоры, круглой в
поперечном сечении (рис. 2). В случае движения к руке приложен движущий момент Mдв. При этом возникают силы
трения F и момент трения MF. Сумма нормальной реакции N и силы трения F дают полную реакцию R,
которая отклонена от нормальной реакции на угол трения ![]() .
.
Записав сумму
моментов всех сил относительно оси опоры О,
получим
|
|
(3) |
|
|
где |
|
|
|
|
|
Рис. 2.
Круг трения |
Следовательно,
|
|
откуда
|
|
(4) |
Круг радиуса ![]() называется кругом
трения. Полная реакция всегда касается круга трения.
называется кругом
трения. Полная реакция всегда касается круга трения.
Можно
использовать форму записи выражения через приведенный коэффициент трения,
полученный для сжатия
|
|
(5) |
Отсюда имеем
|
|
(6) |
В технических
приложениях, например, для цилиндрических подшипников скольжения, ввиду малости трения упрощают формулы, в
конечном итоге заменяя функцию синуса угла
трения коэффициентом трения f.
Данный прием позволяет получить уравнения для сил и моментов сил трения,
выполнить расчеты по которым достаточно просто.
В биомеханике,
рассматривая фрикционные явления в зоне контакта руки с опорой, приходится
иметь дело со случаем значительной величины трения, поэтому все дальнейшие
преобразования в подобном ключе неправомерны.
Распределение давления на контактной поверхности
Для учета трения
в контакте спортсмена с опорой необходимо знание закона распределения давления
на контактной поверхности. Рассмотрим несколько случаев, взяв в качестве
аналога методы исследования подшипников скольжения, применяемые для технических устройств. Основываться
будем на работе [6].
|
|
|
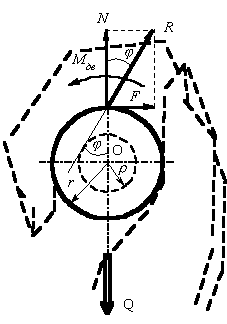
Рис..3. Распределение давления на опоре: а) рука неподвижна; б) рука в движении |
Опишем картину
контактного взаимодействия тел в паре «рука – опора» следующими случаями:
1. Рассмотрим
состояние виса. В неподвижном состоянии рука опирается на опору по цилиндрической
поверхности. Смазка отсутствует.
Линия действия
внешней силы будет проходить через центр опоры O (рис. 3, а).
Воспользуемся
решением контактной задачи теории упругости о сжатии цилиндрических
поверхностей с близкими радиусами (решение И. Я. Штаермана).
Приближенно
закон распределения давлений по контактной поверхности аппроксимируется
параболической зависимостью:
|
|
(7) |
|
|
где |
|
|
Закон
распределения давления в контакте показан на рисунке 3, а.
Составим
уравнение равновесия для одной руки, используя выражение (7). Проинтегрировав,
получим:
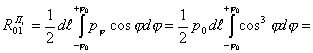
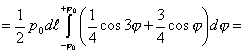
|
|
(8) |
откуда
|
|
(9) |
|
|
где |
|
|
2. В случае
вращения руки вокруг опоры картина взаимодействия человека и спортивного снаряда существенно
усложняется.
Под воздействием
сил трения рука обкатывает опору, и эпюра распределения давлений становится
асимметричной (рис. 3, б). Следует
учесть и сложное поведение тканей руки. Точное решение такой задачи сопряжено и
со значительными трудностями, и со многими неизвестными. Примем в первом
приближении, как и для случая подшипников скольжения, следующее распределение
давлений
|
|
(10) |
Подставив
значение ![]() из формулы (9), получим
из формулы (9), получим
![]()
|
|
(11) |
|
|
|
(12) |
|
|
где |
|
|
Данный вывод для
контакта руки с порой полностью базируется на тех же соображениях, что и выводы
для цилиндрических подшипников скольжения, применяемых в технических
устройствах и в этой части повторяет
материал, изложенный в работе [6]. Для получения более точных моделей трения,
пригодных к использованию в биомеханике, требуются более глубокие исследования
контактного взаимодействия биологических тканей с внешней средой.
Трение с учетом анатомии кисти
Кисть руки,
осуществляющая хват, представляет собой более сложную конструкцию, чем любой
подшипник скольжения.
Укажем, что движение
в суставах кисти и пальцев производят мышцы предплечья и кисти.
Отметим по
поводу мышц кисти, что они располагаются только на ее ладонной поверхности. Что
же касается тыльной поверхности, то на ней самостоятельных мышц нет – там проходят только сухожилия длинных
разгибателей пальцев и в глубине расположены межкостные мышцы [7].
На ладонной поверхности кисти располагаются
три группы мышц: латеральная, образующая возвышение большого пальца,
медиальная, образующая возвышение мизинца, и средняя группа мышц, расположенная
между ними. В состав возвышения большого пальца входят четыре коротких мышцы,
производящие сгибание, приведение, отведение и противопоставление большого
пальца.
Существуют и
другие группы мышц, вызывающие сгибание пальцев [8].
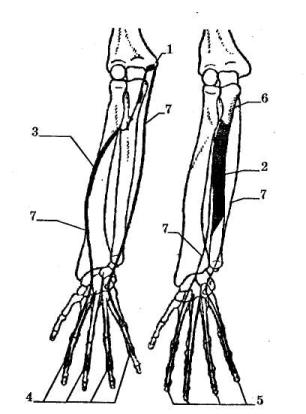
На рисунке 4
показаны схемы прикрепления мышц на ладонной поверхности правой руки.
Анализ строения
кисти и прикрепления мышц показывает, что хватательные движения руки
осуществляется целой группой мышц. Вполне допустимо предположить, что силы,
возникающие при удержании опоры в руке, будут различны в различных частях
контактной поверхности. Это подтверждается практикой. Так, например, в
различных видах единоборств известно, что самым слабым пальцем на руке является
мизинец.
Кроме различных
силовых возможностей пальцев, давление в контакте не будет распределено
равномерно еще и по той причине, что пальцы огибают опору, создавая
многоугольник по периметру.
|
|
|
Рис. 4.
Схемы прикреплений (правая
сторона, ладонная поверхность): а) поверхностного сгибателя пальцев; б) глубокого сгибателя пальцев; |
|
1, 2, 3, 4, 5 – места прикреплений (1 – на плечевой кости; 2 – на локтевой кости, вся зачерненная область; 3 – на лучевой
кости; 4 – на основании средних фаланг; 5 – на основании концевых
фаланг); 6 – место прикрепления на
локтевой кости (обозначено точками, т.к. находится на задней стороне локтевой кости и не
видно); 7 – свободные края мышц |
При этом кости руки
прижимаются к опоре через биологические ткани, распределяющие усилия прижатия
неравномерно под каждой фалангой и ладонной поверхностью, как в статике, так и
в динамике.
Неравномерное распределение нагрузки имеет место как в
продольном сечении (рис. 5), так и в поперечном.
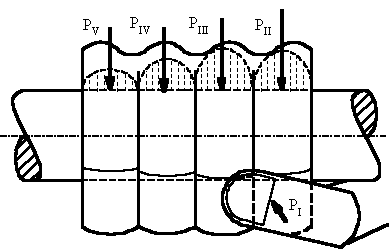
На рисунке 5
показано условное распределение усилий между всеми пальцами руки. Общие силы,
осуществляющие прижим каждого пальца, и тем самым, замыкающие кинематическую
пару «рука – опора» силовым способом, показаны как PI, PII, PIII, PIV, и PV.
Рассматривая хват рукой, необходимо обращать внимание на
отличное от других положение большого пальца I, что дает ему возможность
располагаться при необходимости с противоположной стороны опоры по отношению к
остальным пальцам.
Рисунок 5
показывает неравномерное распределение вдоль опоры усилий, развиваемых каждым
пальцем. Фаланги и пястные кости ладони прижимаются к опоре через ткани руки,
которые, во-первых, распределяют давление по поверхности, а во-вторых, дают
возможность руке смещаться из-за деформации этих тканей.
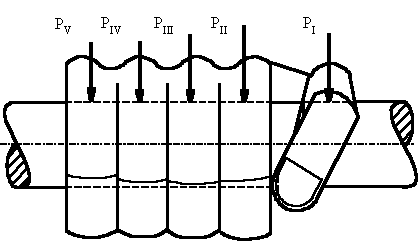
Возможен и другой вариант хвата, показанный на
рисунке 6. Здесь все пальцы находятся с одной стороны перекладины.
|
|
|
Рис. 5.
Распределение нагрузки по пальцам |
По поводу закона
распределения давлений на контактной поверхности без дополнительных
исследований сказать что-нибудь сложно. На данном этапе принимаем в качестве
гипотезы закон распределение давления, выведенный для цилиндрических
поверхностей с близкими радиусами (решение И. Я. Штаермана). Зависимость
используется в расчетах цилиндрических подшипников скольжения.
Другим моментом
является смещение эпюры давления при движении руки и соответственно
суммарной реакции в
каждом контакте пальцев и
ладони по причине
|
|
|
Рис. 6.
Хват пальцев с одной стороны |
податливости тканей кисти.
Это аналог смещения в цилиндрических шарнирах,
происходящего из-за наличия
зазора между подшипником и цапфой.
Величина такого зазора в технике составляет максимум несколько десятых долей
миллиметра. Ткань же смещается на значительную величину: достаточно нажать на
любое место своей руки и посмотреть, как сильно деформируется эта зона.
Кроме того, конструкция руки с точки зрения
механики представляет собой динамическую цепь, которая может подстраиваться под
охватываемую поверхность и перераспределять усилия между мышцами,
осуществляющими хват. Анализ показывает сложный характер контакта костей с охватываемой поверхностью по ряду
причин, одна из которых это криволинейность поверхности костей.
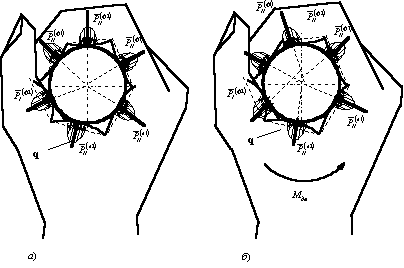
|
|
|
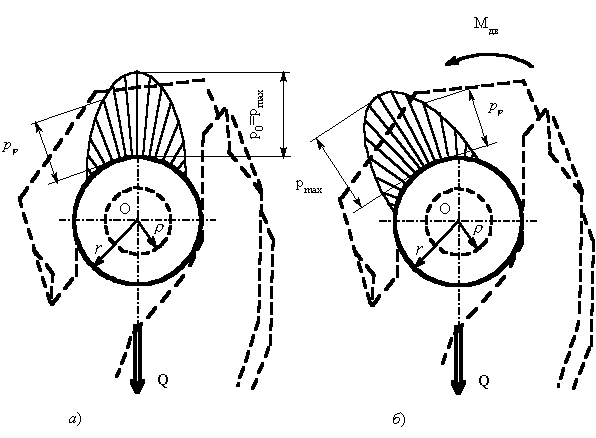
Рис. 7. Давление костей на опору: а) в статике; б) в движении |
На рисунке 7, а показано возможное распределение давления
на контактной поверхности в случае статического положения руки, а на рисунке 7,
б – в движении.
Заключение
Кроме наличия
трения как такового и его величины, необходимым моментом при осуществлении
движения спортсменом в контакте со снарядом является выполнение условий
удержания рукой опоры. В случае сжатия круглой опоры с разных сторон, условием
сохранения контакта является равенство или превышение суммарной силой трения
величины полной силой, с которой человек сжимает опору.
Значительная
величина коэффициента трения обуславливает разработку отдельной методики
расчета всех параметров трения, не совпадающую с принятой для расчета трения
цилиндрических шарниров. При этом анатомия кисти, свойства биологической ткани
руки, а также тип хвата, используемого во время выполнения спортивного
упражнения, оказывают влияние на
методы, применяемые для получения расчетных моделей.
ЛИТЕРАТУРА
1.
Коренев Г. В. Введение в механику
человека /Г.В. Коренев. - М.: Наука, 1977. - 264 с.
2.
Загревский В. И. Расчетные модели кинематики
и динамики биомеханических систем /В. И. Загревский. - Томск-Могилев:
Издательская лаборатория Томского педагогического университета, 1999. - 156 с.
3.
Покатилов А. Е. Биомеханика взаимодействия
спортсмена с упругой опорой /А. Е. Покатилов; под. ред. В.И. Загревского. – Минск: Изд. центр БГУ, 2006. – 351 с.
4.
Артоболевский И. И. Теория механизмов и машин:
учеб. для втузов /И. И. Артоболевский. – М.: Наука, 1988. – 640 с.
5.
Бегун П. И. Моделирование в
биомеханике: учеб. пособие / П. И. Бегун,
П. Н. Афонин. – М. : Высш. шк., 2004. – 390 с.
6.
Дмитриев В. А. Детали машин /В. А.
Дмитриев. – Л.: Судостроение, 1970. – 792 с.
7.
Боянович Ю. В. Атлас анатомии человека /
Ю. В. Боянович, Н. П.. Балакирев.
– Ростов на Дону.; Феникс, Харьков. : Торсинг, 2005. – 734, [1] с.
8.
Фениш Х. Карманный атлас анатомии
человека на основе Международной номенклатуры / Х. Фениш (при участии В.
Даубера). – Мн.: Вышэйшая школа, 2001. – 464 с.
CONDITION
OF DEDUCTION OF THE SUPPORT IN THE HAND
Pokatilov
A.E., Zagrevskij V.I., Popov V. N., Maksimova M.V., Chuhmakova S.A.
For many sports disciplines deduction of
contact to a shell is the determining factor influencing finally on an
estimation of exercise and a opportunity of its performance. Conditions of
deduction of a round support, type of a crossbeam in sports gymnastics are
considered. Some kinds of models are offered. The concept of a circle of
friction and methods of calculation of parameters of frictional contact in view
of significant size of factor of friction on a contact surface is analysed.
Feature of basic cinematic
pair «a shell - the hand» is presence of the soft biological fabrics deformed
during movement of the sportsman. There is a displacement of basic reactions
and forces of friction by analogy to bearings of sliding of technical devices.
This factor influences models of friction.
In a general view influence of anatomy of a brush on distribution of contact pressure between fingers of a hand and a palm is described. Displacement of pressure during movement of the person for each finger of a hand is shown.
Key words: sport gymnastic,
biomechanic.
Кафедра прикладной механики
Могилевский государственный
технологический институт
Поступила
в редакцию 5.12.2008.