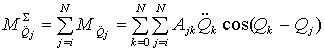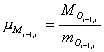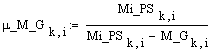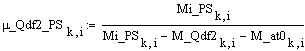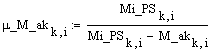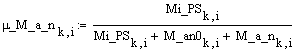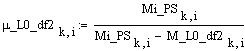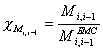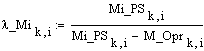Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 8. -

Вып. 1. - 2009. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ

http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/TITL-21.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/cont.htm

 

УДК 532.5+591.173+591.174

АНАЛИЗ ЦЕЛЕНАПРАВЛЕННОГО ДВИЖЕНИЯ ЧЕЛОВЕКА

 

Ó 2008 г. Покатилов А.Е., Попов В.Н., Загревский В.И., Кравцова И. М., Тржецецкая Л. О.

 

(popov-3.doc)

 

Представлен анализ управляемого движения спортсмена, определяемого как целенаправленное, на примере большого оборота назад на перекладине. Движение описывается теоретической моделью, в которой учтено влияние упругой опоры. Показано несколько вариантов моделей движения, в которых члены уравнений сгруппированы по видам ускорений, по силовым факторам, а также по принадлежности к механической и биомеханической системам. В предложенной методике анализа введены понятия коэффициентов влияния силовых факторов и коэффициентов опоры, позволяющие оценить долю исследуемого фактора в полной величине моментов управляющих сил, записанных относительно суставов тела и опорной кинематической пары. 

Ключевые слова: анализ движения спортсмена, биомеханическая система.

 

Введение

 

При исследовании движения спортсмена в первую очередь необходимо обратить внимание на целенаправленное движение человека, т.е. на движение при котором  для управления внутри тела вырабатываются мышечные силы [1].

Так как  ни величина, ни  направление,  ни точка  приложения  к звену каждой управляющей силы и в каждый момент времени неизвестны, то принято эти силы приводить к соответствующим шарнирам. При этом появляются пары управляющих сил (моменты управляющих сил). В такой постановке задача исследования движения имеет решение.

В результате использования указанного приема получаем приложенные к суставу силы реакции и управляющие силы, а также  действующий на звено момент управляющих сил относительно исследуемогошарнира .

Отметим, что одним из возможных методов анализа движения можно выбрать метод кинетостатики. Практика показывает, что его применение позволяет расширить ряд факторов, включаемых в исследование. В качестве примера можно привести трение в опорной паре, исследование которого с помощью уравнений Лагранжа второго рода требует использования дополнительных методов, так как выражения применимы только в случае идеальных связей [1-4]. 

Модели целенаправленного движения спортсмена

Исследовался большой оборот назад, выполняемый на перекладине олимпийского образца. В качестве примера из всего спортивного упражнения взят один оборот, составляющий примерно 360°. Движение человека фиксировалось видеокамерой с частотой съемки 25 кадров в секунду. Вторая видеокамера регистрировала перемещение спортивного снаряда.  Отметим, что методы сглаживания могут оказывать значительное влияние на начало и окончание сглаживаемой зависимости, по этой причине первоначально брался более широкий интервал с запасом в 10 кадров до начала исследуемого участка, и в 10 кадров после его окончания. Общее количество отобранных кадров составило 72, а для последующего биомеханического анализа из них взято 52. В дальнейшем для всех необходимых расчетов и графиков отсчет кадров на анализируемом участке начинается с 0, при этом отбрасывается запас в начале и в конце таблицы исходных данных.

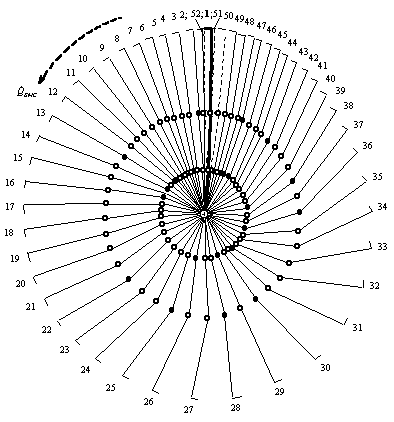
Кинетограмма упражнения показана на рисунке 1. Биомеханическая система моделируется трехзвенником – звеньями являются руки, туловище и ноги. Начальное положение биомеханической системы (БМС) выделено сплошной толстой линией, три последних – штриховой. Направление вращения спортсмена – против часовой стрелки. Оно считается положительным.

 

 

Рис. 1. Кинетограмма большого оборота на перекладине

При этом кинетограмма на рисунке 1 показывает движение спортсмена со стороны камеры,  фиксирующей перемещение спортивного снаряда.   Если рассматриваемая фаза упражнения для звена длится больше оборота, то это учитывается в значениях обобщенных координат – на втором круге угловые координаты больше 360°.

Взятое для исследования маховое упражнение выполнял мастер спорта Ю. К., 1980 г. р. Параметры тела, необходимые для кинематического и динамического анализов, рассчитаны по специальной методике, представленной в работе [5].

 

Анализ уравнений целенаправленного движения человека

 

Уравнение целенаправленного (управляемого) движения имеет вид [6]

.

(1)

Здесь коэффициенты, учитывающие массу звеньев и их размеры, равны:

        

                      ,          если , 

       =

                      ,                      если i>j,

 

(2)

i=1, 2, …, N;   j=0, 1, …, N;   .

 

 

Аналитическое выражение коэффициентов для вычисления момента управляющих сил N-звенной биомеханической системы в условиях упругой опоры построим, введя символ Кронекера. Последний равен

 

 

                          1,             если i=j,

         =

                          0,             если i¹j.  

 

(3)

 

Здесь i, j – буквенные индексы, соответствующие цифровым индексам коэффициентов Aij.

 

,

(4)

где

i=1, 2, …, N;  j=1, 2, …, N;  .

 

Коэффициенты, характеризующие опору, являются переменными , в отличие  от коэффициентов для биосистемы Aij=const, где , .

Уравнение целенаправленного движения (1) хорошо структурировано.

Рассмотрим этот момент подробнее. Формула (1) разбита на пять однотипных групп по видам ускорений. Обозначим:

1.  – сумма моментов от сил тяжести звеньев исследуемой части биомеханической системы. Характеризует влияние сил тяжести звеньев, начиная с текущего i-го звена и до крайнего (до ног). Имеем

.

(5)

2.  – сумма моментов от сил инерции звеньев исследуемой части биомеханической системы в поступательном движении при прогибе опоры (растяжении-сжатии пружины, моделирующей снаряд). Характеризует часть движения, определяемую через силы инерции звеньев при поступательном движении опоры (растяжение или сжатие пружины), начиная с текущего i-го звена в сторону крайнего. Запишем сумму как

.

(6)

3.  – сумма моментов от кориолисовых сил инерции, прикладываемых к звеньям исследуемой части биомеханической системы. Характеризует часть движения звеньев, начиная с текущего i-го звена в сторону крайнего, состоящую из одновременного поступательного движения их ЦМ за счет линейного перемещения опоры и вращения ее упругой линии  (точнее пружины, моделирующей упругие свойства спортивного снаряда), т.е. за счет обращения опоры. Имеем

.

(7)

4.  – сумма инерционных моментов, характеризующих неравномерность вращения звеньев. Появляется при наличии угловых ускорений звеньев биомеханической системы. Сумма равна

.

(8)

5.  – сумма моментов от центробежных сил инерции звеньев биомеханической системы через коэффициенты  примет вид

.

(9)

Запишем уравнение движения (1) через группы, отражающие виды ускорений при движении относительно любого сустава или опорного шарнира , как

.

(10)

Введем коэффициенты влияния моментов

,

(11)

где

 – коэффициент влияния исследуемого момента;

 – управляющий момент относительно шарнира, Н×м;

 – суммарный момент относительно шарнира без учета исследуемого силового фактора, Н×м.

 

Выполним анализ уравнения движения в математическом редакторе  Mathcad 14.0. Программа представлена в листинге 1.

 

Листинг 1. Анализ структуры уравнения движения

 

Коэффициенты влияния составляющих момента управляющих сил       

     по силам тяжести – 

           

     по инерционным силовым факторам, определяемым по угловому ускорению  –

         

     по кориолисовым  силам инерции – 

           

     по нормальным силам инерции –

                           

     по силам инерции в поступательном движении опоры (растяжение-сжатие пружины) –  

         

 

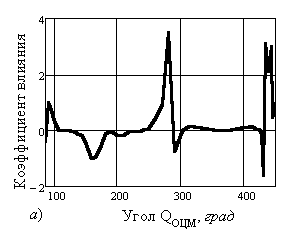
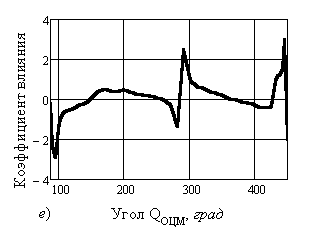
Рассмотрим изменение рассчитанных коэффициентов влияния силовых факторов по углам QОЦМ  общего центра масс БМС. В связи с большим объемом материала, здесь покажем влияние только моментов сил тяжести и инерционных моментов, определяемых по угловым ускорениям . К последним относятся как дополнительные моменты  сил инерции, так и моменты касательных сил инерции звеньев биомеханической системы. На рисунках 2, а–е представлены графики, показывающие изменение влияния рассматриваемых силовых факторов в зависимости от углового положения общего центра масс биомеханической системы.

Отметим следующий момент: все графики для коэффициентов влияния моментов силовых факторов относительно каждого шарнира показывают всплески и провалы в значениях коэффициентов. При этом каждый силовой фактор может в разы и даже в десятки раз менять значение управляющего момента (например, рис. 2, а  и рис. 2, г), что,  конечно же, вызывает вопросы.   Если каждый фактор так сильно влияет на результат, то, что получим в сумме? Вывод здесь следующий: во-первых, не обязательно всплески значений всех силовых факторов происходят одновременно, а во-вторых, возможно наложение всплесков и провалов в значениях, нивелирующее друг друга.

 

 

 

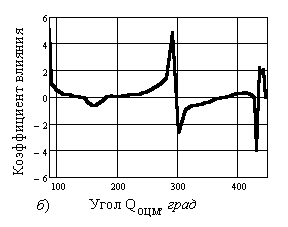
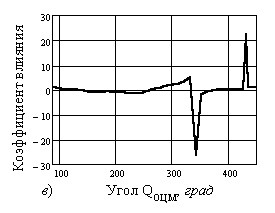
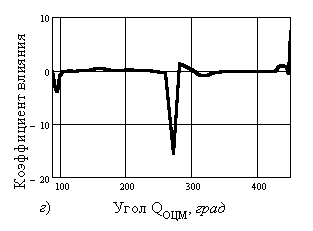
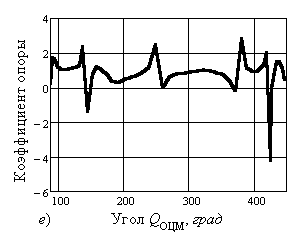
Рис. 2. Изменение коэффициентов влияния силовых факторов в

зависимости от угла QОЦМ  для моментов от:

– сил тяжести относительно:

    а) – опорного шарнира; б) – плечевого сустава;

    в) – тазобедренного сустава;

– инерции, определяемой по угловым ускорениям  

звеньев во вращении относительно:

   г) – опорного шарнира; д) – плечевого сустава;

   е) –тазобедренного сустава

 

Кроме того, силовые факторы, даже без резких скачков, могут быть разнонаправленными, т.е. иметь противоположные знаки. При суммировании каждой пары моментов полученное значение окажется меньше любого из слагаемых, хотя коэффициент влияния может иметь достаточно большое значение. 

Так же укажем на относительный, а не абсолютный характер коэффициентов, т.е. всплеску на графике не обязательно соответствует большое значение исследуемого фактора.

 

Динамическое усиление движения человека спортивным снарядом

 

Выделенные системы дают представление о динамическом усилении движения спортсмена упругой опорой в явной части, т.е. без учета влияния деформации спортивного снаряда на величину обобщенных координат биомеханической системы.

Используя уравнение целенаправленного движения (1), запишем выделенную опору как

.

(12)

Другая часть выражения показывает связь параметров движения непосредственно спортсмена с моментами управляющих сил. Это выделенная биомеханическая система, но с измененными упругой опорой параметрами движения, имеющая вид:

.

 

(13)

Управляющий момент мышечных сил на i-ом звене является суммой моментов, отражающих влияние движения биомеханической системы и деформации опоры (ее движения):

.

(14)

Выполненное разделение изучаемой характеристики движения по системам позволяет оценить влияние биомеханической системы на упругую опору через коэффициент опоры по моменту управляющих сил. Для каждого шарнира он имеет вид

.

(15)

Выполним анализ динамики полной системы через коэффициенты опоры по моментам управляющих сил  в листинге 2. Программа получается весьма компактной и легко читаемой.

 

Листинг 2. Оценка динамики полной системы при группировке

членов уравнения движения по видам ускорений

Коэффициент опоры по моменту управляющих сил:       

 

                           

 

Момент управляющих мышечных сил выделенной биомеханической системы определен через разность момента полной системы и момента выделенной опоры. Вычисления производятся по всем кадрам и относительно всех шарниров.

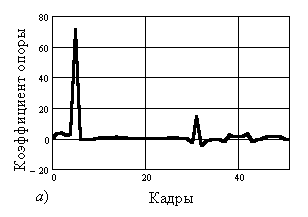
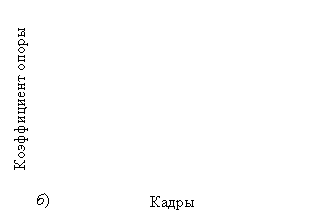
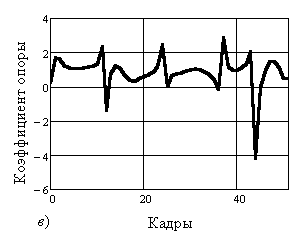
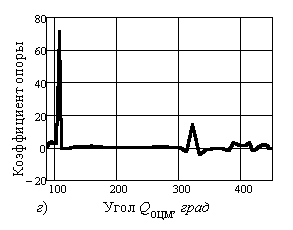
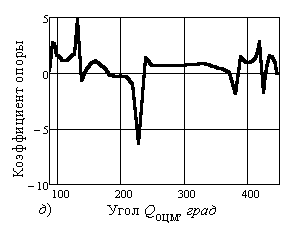
Рисунки 3, а–в  иллюстрируют изменение коэффициентов опоры по кадрам, а рисунки 3, г–е – в зависимости от углового положения общего центра масс биомеханической системы. Графики, показывающие зависимость коэффициентов от времени (по кадрам) и от углового положения ОЦМ спортсмена подобны друг другу, различаясь лишь масштабом.

Анализ показывает, что наибольшее влияние опора оказывает на управляющий момент относительно опорного шарнира, среднее – на момент относительно плечевого сустава, и наименьшее – на момент относительно сустава тазобедренного. Другими словами, чем дальше шарнир расположен от спортивного снаряда, тем меньшая доля управляющего момента приходится на упругую опору.

 

 

 

 

 

Рис. 3. Изменение коэффициентов опоры для момента

управляющих сил:

 по кадрам относительно:

а) – опорного шарнира; б) – плечевого сустава; в) – тазобедренного сустава; 

 по угловому положению ОЦМ относительно:

 г) – опорного шарнира; д) – плечевого сустава; е) – тазобедренного сустава 

 

Другой чертой являются всплески значений коэффициента. При этом для опорного сустава они так велики, что в остальные моменты кривая представляется в виде почти прямой линией из-за большого масштаба рисунка. Для управляющих моментов относительно плечевого и тазобедренного суставов резкие изменения моментов соизмеримы с их средними значениями за весь оборот.

 

Заключение

 

В зависимости от критерия, на основании которого группируют однотипные члены уравнения движения, оно разбивается на две пять или шесть групп. Использование коэффициентов влияния позволяет оценить воздействие каждого силового фактора, используемого в кинетостатических расчетах биомеханической системы, на моменты управляющих сил мышечной системы.

С другой стороны, движение спортсмена в условиях опоры является суммой движений двух разных систем: механической, представленной спортивным снарядом, и биомеханической, представленной самим человеком. Отмеченный момент позволяет модели движения разбить на две отдельные части, отражающие движение этих систем в явном виде. Таким образом, с помощью коэффициента опоры по управляющему моменту можно оценить динамическое усиление движения, вызываемое спортивным снарядом с упругими свойствами.

 

ЛИТЕРАТУРА

1.     Коренев Г. В. Введение в механику человека /Г.В. Коренев. - М.: Наука, 1977. - 264 с.

2.     Артоболевский И. И. Теория механизмов и машин: учеб. для втузов /И. И. Артоболевский. – М.: Наука, 1988. – 640 с.

3.     Бать М. И. Теоретическая механика в примерах и задачах : в 2 т. /М. И. Бать, Г. Ю. Джанелидзе, А. С. Кельзон; под общ. ред. Г. Ю. Джанелидзе и Д. Р. Меркина. – М. : Наука, 1991. – Т.2. – 640 с.

4.     Никитин Н. Н. Курс теоретической механики /Н. Н. Никитин. – М.: Высшая школа, 1990. – 608 с.

5.     Загревский В. И. Расчетные модели кинематики и динамики биомеханических систем /В. И. Загревский. - Томск-Могилев: Издательская лаборатория Томского педагогического университета,  1999. - 156 с.

6.     Покатилов А. Е. Биомеханика взаимодействия спортсмена с упругой опорой /А. Е. Покатилов; под. ред. В. И. Загревского. – Минск: Изд. центр БГУ, 2006. – 351 с.

 

THE ANALYSIS OF PURPOSEFUL MOVEMENT OF THE PERSON

 

 Pokatilov A.E., Popov V. N., Zagrevskij V.I., Kravtsov I.M., Trzhetsetskaja L.O.

 

The analysis of operated movement of the sportsman determined as purposeful, on an example of the big turn back on a crossbeam is presented. Movement is described by theoretical model in which influence of an elastic support is considered. Some variants of models of movement in which members of the equations are grouped by kinds of accelerations, under power factors, and also on an accessory to mechanical and biomechanical systems are shown. In the offered technique of the analysis concepts of factors of influence of power factors and factors of the support are entered, allowing to estimate a share of the researched factor in full size of the moments of the operating forces which have been written down concerning joints of a body and basic cinematic pair.

Key words: analysis of operated movement of the sportsman, biomechanical systems.

 

Кафедра прикладной механики

Могилевский государственный технологический институт

Поступила в редакцию 5.12.2008.