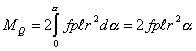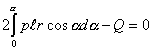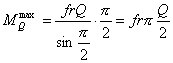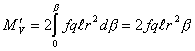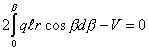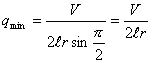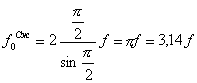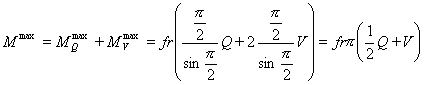Математическая морфология.
Электронный математический и медико-биологический
журнал. - Т. 8. -
Вып. 1. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/TITL-21.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/cont.htm
УДК 532.5+591.173+591.174
МОДЕЛИРОВАНИЕ ТРЕНИЯ В ОПОРНОЙ ЧАСТИ РУКИ
Ó 2008 г. Попов В. Н., Покатилов А. Е., Загревский В.
И., Максимова М. В.,
Чухмакова С. А.
При моделировании движения спортсмена часто
появляется задача математического описания контактного взаимодействия
человеческой руки со спортивным снарядом. Важнейшим аспектом такого
взаимодействия является трение. Показано влияние решаемых задач движения на модели трения. Анатомические особенности
кисти руки позволяют с одной стороны обеспечить контакт со снарядом во время
выполнения спортивного упражнения на перекладине в спортивной гимнастике, а с
другой стороны дополнительно сжимать опору вне зависимости от требования
силового замыкания опорной кинематической пары. Даны расчетные модели для обоих
случаев. Третий случай является суммой двух первых, учитывая сохранение
контакта в движении и возможное дополнительное всестороннее сжатие опоры.
Ключевые слова:
моделировании движения спортсмена, биомеханическая система.
Введение
В теоретической
механике по одному из признаков связи разделяют на удерживающие (налагаемые ими ограничения сохраняются при любом
положении системы) и неудерживающие, не
обладающие этим свойством (система от таких связей может «освобождаться»).
Связи,
реализуемые в суставах биомеханической системы (БМС), относят к неудерживающим, теория которых разработана
слабо [1].
По поводу же
руки, удерживающей опору, можно высказать следующие соображения:
- кинематическая
пара, образованная рукой при обхвате, например, грифа перекладины, имеет,
прежде всего, силовое замыкание, и только как следствие этого, при контакте
сохраняется замыкание геометрическое;
- состояние
данной связи зависит не только от силовых возможностей биомеханической системы,
но и от желания человека. Подобный пример в технике возможен лишь в устройствах
подобных манипуляторам, управление которых осуществляется специальными
системами. При этом в любом случае с позиции силового замыкания кинематической
пары между манипулятором и кистью существует
серьезное различие, обусловленное выносливостью мышечной системы.
Таким образом, в
определенные моменты времени кинематическая пара «рука – опора» может
представлять собой удерживающую связь, которую разорвать не получится. Зависит это как от желания человека, так и
от силовых возможностей мышц, а также их выносливости.
В другие же
моменты связь оказывается неудерживающей, что как может зависеть от воли
человека, так может и не зависеть, когда у спортсмена не хватает выносливости
или силы. В качестве примера можно привести выполнение виса. В первоначальный
момент у тренированного спортсмена связь, образованная кистью и опорой
необходимо отнести к удерживающей, если у спортсмена есть желание ее сохранить.
Но с течением времени, независимо от подготовки спортсмена, связь станет
неудерживающей. Ведь понятно, что сохранить ее удерживающей в течение
длительного времени не представляется возможным.
Таким образом,
мы пришли к заключению, что связь «рука – опора» в зависимости от
продолжительности действия и ряда дополнительных факторов, может менять свое
состояние, т.е. переходить от удерживающей к неудерживающей и наоборот. По сути
дела она является переходной, т.е. переменной. И несомненно, что на пару «рука
– опора» серьезное влияние оказывает трение.
Математические модели трения пары «рука – опора»
Так как явления,
реализуемые во фрикционном контакте, имеют весьма сложную природу, то начнем с
определенных ограничений, позволяющих установить основные закономерности трения руки о металл.
В триботехнике
выработаны определенные подходы при изучении трения в технических устройствах.
Возьмем из данной области некоторые
идеи, приложение которых к биологическим объектам не вызывает возражений.
При описании процессов фрикционного взаимодействия
человека и спортивного снаряда применим ряд упрощенных моделей.
В разделах механики, занимающихся исследованием
механизмов и машин, имеются устройства, которые могут служить если и не в качестве
аналогов, то, по крайней мере, в качестве отправных точек для наших
исследований трения. Это всевозможные подшипники скольжения, изучаемые в
деталях машин [2], теории механизмов и машин [3] и в триботехнике [4]. Введем ограничения. Считаем, что:
1.
объемные
деформации спортивного снаряда (опоры) пренебрежимо малы по сравнению с
объемными деформациями тела (руки);
2.
площадь
контакта в паре «рука – опора» в общем случае является величиной переменной;
3.
деформации контр-тела (руки) упругие;
4.
сила
трения имеет молекулярно-механическую природу;
5.
сила
трения равномерно распределена по ширине ладони;
6.
фрикционное
взаимодействие руки с опорой происходит в отсутствии смазки.
В работе [5] рассмотрено трение во вращательной
кинематической паре в условиях сухого трения. Принятые здесь допущения по
трению в паре «рука – опора» несколько отличаются от допущений, используемых
при анализе трения в теории механизмов и машин, но сам подход является весьма
полезным и его можно взять на вооружение.
|
|
|
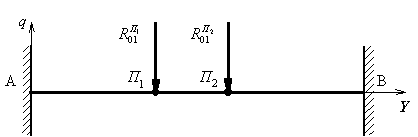
Рис. 1. Силы, действующие на опору со стороны двух рук |
На опору в
шарнирах 
и 
со стороны каждой
руки действует реакция 
(рис. 1). Так как имеем
два таких шарнира (по числу рук), то возникающие реакции обозначим как 
и 
. Здесь 
и 
– это левый и правый
шарниры.
В общем случае,
когда не надо конкретизировать пару,
реакцию будем записывать с верхним индексом 
. Те же цифровые индексы относятся и к соответствующим
параметрам трения. Для анализа возьмем случай равенства реакций в обоих
шарнирах «рука – опора». Также отметим, что опорные реакции вращаются из-за
вращения самой биомеханической системы, вызывая обращение рабочей части
спортивного снаряда [6].
Реакции в каждом
опорном шарнире компенсированы 
. Здесь 
есть сила, действующая
со стороны опоры 0 на руку 1 спортсмена
в шарнире 
, а реакция 
– результат действия руки 1 на опору 0 в том же шарнире.
Рассматривая направление сил, будем считать в первом приближении, что реакции связей
действуют на балку со
стороны вогнутости упругой линии, так как именно они и вызывают этот прогиб.
Анализ различных
случаев контакта руки человека с опорой в виде балки круглого поперечного
сечения дает возможность выделить два варианта контакта. Рассмотрим их на
примере виса спортсмена на перекладине.
|
|
|
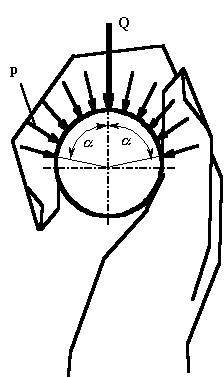
Рис. 2.
Контакт руки с опорой в случае виса спортсмена |
1. Считаем, что при
осуществлении виса достаточно, чтобы рука охватывала гриф перекладины
наполовину или даже несколько меньше. Такую связь необходимо удерживать как в статике, так и в динамике. В качестве
общего случая рассмотрим контакт руки с опорой, когда угол охвата составляет
величину 
(рис. 2), при этом
выполняется условие 
.
2. Охват рукой
круглой опоры и ее удержание также возможно осуществить сжатием последней с
произвольным усилием. При этом внешняя нагрузка может отсутствовать.
Реальный случай
на практике часто является суммой обоих вариантов. Рассмотрим их по порядку.
Первый случай. Применим гипотезу Вейсбаха о
постоянном давлении. Исходя из нее, считают, что удельное нормальное давление
распределено равномерно по всей площади контакта, т.е. 
.
Покажем действие
силы Q, направленной со стороны
руки на спортивный снаряд (рис. 2) при висе спортсмена, и возникновение
элементарной реакции dN
со стороны опоры. Для этого выделим на
опоре полоску вдоль образующей цилиндра длиной 
. Это ширина ладони. Пусть полоска имеет бесконечно малую
ширину 
(рис. 3). Площадь
полоски равна
|
|
(1) |
Нормальное
давление на эту полоску равно
|
|
(2) |
Сила трения на
полоске
|
|
(3) |
Момент трения на
такой элементарной полоске равен
|
|
(4) |
Полный момент 
сил трения по всей поверхности
найдем как сумму элементарных моментов трения по всему контакту
|
|
(5) |
|
|
|
||
|
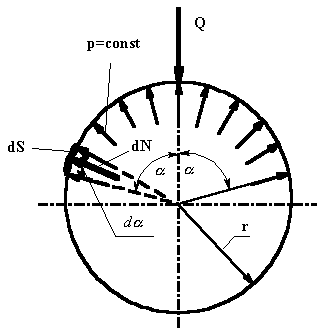
Рис. 3. Расчетная схема в случае виса спортсмена |
||
В предельном
случае при 
имеем
|
|
(6) |
Для определения
нормального удельного давления p
возьмем сумму проекций всех сил на вертикаль (рис. 3):
|
|
(7) |
Проинтегрировав,
получим
|
|
(8) |
,и тогда запишем
|
|
(9) |
Нами получено,
что удельное давление равно силе, деленной на площадь проекции опорной части
цилиндра [3].
Подставим
удельное нормальное давление p в
уравнение момента трения (5). Получим
|
|
(10) |
или
|
|
(11) |
|
|
где |
|
|
При 
, т.е. в случае, когда охват рукой составляет собой
полуокружность, приведенный коэффициент трения равен
|
|
(12) |
а сам момент запишем как
|
|
(13) |
Рассмотренный
здесь вариант имеет своим аналогом в теории механизмов и машин цилиндрический
подшипник скольжения [3, 5].
Второй случай. В случае охвата и
сжатия рукой опоры будем исходить из
следующих предположений:
- применима
гипотеза Вейсбаха о постоянном давлении;
- рука
охватывает боковую поверхность опоры с противоположных сторон таким образом,
что контактные зоны располагаются симметрично относительно обеих координатных
осей: ординаты и аппликаты. Другие случаи здесь не рассматриваются.
|
|
|
Рис. 4.
Сжатие рукой опоры |
Охват рукой рукой
всего периметра поперечного сечения опоры представлен на рисунке 4. Это частный
и предельный случай.
Все шаги по
выводу необходимых уравнений повторяются, как и для первого варианта.
Начнем анализ
при охвате рукой опоры на угол 
, но зон контакта с таким углом две и расположены они с
противоположных сторон. Именно в этом случае обеспечивается фиксация
рассматриваемого предмета в руке. С противоположных сторон на опору действуют
равные силы 
, создавая на контактных поверхностях руки с опорой
равномерное давление q.
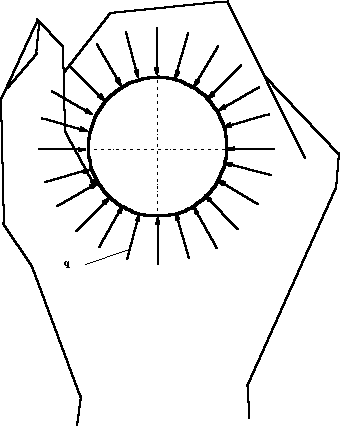
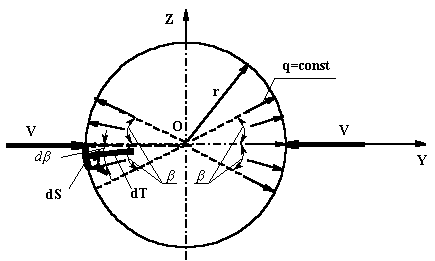
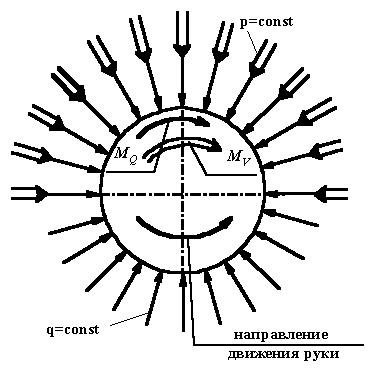
На рисунке 5
дана расчетная схема для случая сжатия опоры с противоположных сторон. Пятна
контакта имеют размеры, ограниченные углом
с каждой стороны
опоры.
|
|
|
Рис. 5. Расчетная схема в случае сжатия рукой
опоры |
Для элементарной
полоски по образующей цилиндра, длиной равной ширине ладони 
и бесконечно малой в
поперечном сечении шириной 
(рис. 5). Площадь
полоски определяется по уравнению (1). Нормальное давление на нее равно
|
|
(14) |
Силу трения и
момент трения на полоске определяют аналогично выражениям (3) и (4)
|
|
(15) |
Момент трения на
такой элементарной полоске равен
|
|
(16) |
Отметим, что при
удержании в руке опоры способом, показанным на рисунке 5, внешние для опоры
силы сжатия V могут быть обе активными, или одна из них активной,
а вторая пассивной. Например, опору можно сжать пальцами, приложив силы с
противоположных сторон, а можно теми же пальцами прижать опору к ладони и т. д.
На анализе это не скажется.
Рассмотрим
равновесие руки по расчетной схеме рисунка 5. Для анализа необходимо взять
каждое пятно контакта в отдельности друг от друга. Для определения момента сил
трения с одной стороны опоры, возникающего при давлении и движении руки,
выполним сложение по контактной поверхности всех элементарных моментов трения.
Здесь угол 
изменяется в пределах
. Получим
|
|
(17) |
Так как
существует два пятна контакта, то полный момент сил трения будет в два раза
больше
|
|
(18) |
Максимальное значение
момента трения получим при 
. Подставив данный предельный угол, запишем
|
|
(19) |
Для определения
нормального удельного давления q достаточно
рассмотреть одно из пятен контакта. Запишем величину давления через проекцию
всех сил на горизонтальную ось OY
|
|
(20) |
Проинтегрировав,
получим
|
|
(21) |
.Отсюда выразим
|
|
(22) |
При максимальном
охвате рукой опоры уравнение примет вид
|
|
(23) |
Отметим, что это
минимальное из всех возможных давлений, так как оно определенно по максимально
возможной площади контакта.
Подставляя выражение
(22) в уравнение момента трения (18), получим
|
|
(24) |
или
|
|
(25) |
Здесь 
равно
|
|
(26) |
При 
, т.е. в случае, когда происходит всесторонний охват рукой
опоры, получим
|
|
(27) |
а момент трения станет
равным
|
|
(28) |
Это максимальное
значение момента сил трения при всестороннем сжатии рукой опоры.
Третий случай. Третий случай является суммой первых двух, т.е. спортсмен
выполняет вис, при этом дополнительно сжимает опору. Расчетная схема показана
на рисунке 6. Тогда получим формулу
для полного момента трения, суммируя
случай виса и случай полного обхвата опоры рукой, выраженные уравнениями (5) и
(18)
|
|
(29) |
При полном
обхвате рукой опоры, согласно формулам
(6) и (19) выражение для максимального значения момента сил трения окажется
равным
|
|
(30) |
Если выразить
момент через силы, а не давления, то получим для общего случая
|
|
(31) |
При 
и 
запишем величину
максимально возможного момента сил трения для третьего случая
|
|
(32) |
|
|
|
||
|
Рис. 6. Силы в контакте спортсмена с опорой в
условиях виса и одновременного и всестороннего сжатия рукой всей
опоры |
||
Уравнение включает в себя суммарную внешнюю
силу 
, в остальной части, не отличаясь от уравнения (13) для полного максимального момента в
случае виса, и от уравнения (28) для всестороннего сжатия опоры.
Назовем эту силу
условной, так как она включает половину внешней нагрузки, возникающей при висе
спортсмена, и одну из двух равных и противоположно направленных сил от сжатия
руки.
Обозначим
условную внешнюю силу как
|
|
(33) |
Тогда формула
(32) примет вид
|
|
(34) |
Учитывая равенство
(27), перепишем выражение через приведенный коэффициент трения. Получим
|
|
(35) |
Подкорректируем
форму записи уравнения (11) для случая виса БМС,
используя приведенный коэффициент трения 
. Запишем
|
|
(36) |
Таким образом,
во всех трех случаях можно использовать приведенный коэффициент трения для
сжатия.
Заключение
Биомеханические
исследования движения спортсмена требуют знания закономерностей фрикционного контакта
человека со снарядом. Уравнения целенаправленного движения в условиях жесткой
[7] и упругой опоры [6] при записи
относительно контакта рук со снарядом содержат момент сил трения. При этом
спортсмены предпринимают меры для его увеличения: используют специальные
накладки и присыпки. Принятые методы оптической регистрации движения с
последующей расшифровкой и определением в вычислительном эксперименте
параметров кинематики и динамики фиксируют движение с учетом внешнего трения.
Конкретная
реализация вида контакта человека со спортивным снарядом зависит от конкретной
фазы упражнения, желания спортсмена и пр. На контакт также оказывает влияние
анатомические особенности строения кисти.
Рассмотренные
здесь модели трения получены исходя из ряда допущений, не учитывающие
особенности поведения мягких биологических тканей [8], распределения усилия
сжатия между отдельными областями руки, кривизны костей [9] и пр.
ЛИТЕРАТУРА
1.
Коренев Г. В. Введение в механику
человека /Г.В. Коренев. - М.: Наука, 1977. - 264 с.
2.
Дмитриев В. А. Детали машин / В. А.
Дмитриев. – Л.: Судостроение, 1970. – 792 с.
3.
Машков А. А. Теория механизмов и машин
/А. А. Машков. – Мн.: Вышэйшая школа. 1971. – 472 с.
4.
Мур Д. Основы и применения
трибоники /Д. Мур. – М.: Мир, 1978. –
488 с.
5.
Артоболевский И. И. Теория механизмов и машин:
учеб. для втузов /И. И. Артоболевский. – М. : Наука, 1988. – 640 с.
6.
Покатилов А. Е. Биомеханика взаимодействия
спортсмена с упругой опорой /А. Е. Покатилов; под. ред. В. И. Загревского. –
Минск: Изд. центр БГУ, 2006. – 351 с.
7.
Загревский В. И. Расчетные модели кинематики
и динамики биомеханических систем /В. И. Загревский. - Томск-Могилев:
Издательская лаборатория Томского педагогического университета, 1999. - 156 с.
8.
Бегун П. И. Моделирование в биомеханике
/П. И. Бегун, П. Н. Афонин. – М.:
Высшая школа, 2004. – 390 с.
9.
Боянович Ю. В. Атлас анатомии человека /
Ю. В. Боянович, Н. П. Балакирев. –
Ростов на Дону.; Феникс,
Харьков: Торсинг, 2005. – 734, [1] с.
MODELLING OF
FRICTION IN THE BASIC PART OF THE HAND
Popov V. N., Pokatilov A.E., Zagrevskij
V.I., Maksimova M.V., Chuhmakova S.A.
At modelling movement of the sportsman often there is
a problem of the mathematical description of contact interaction of a human
hand with a sports shell. The major aspect of such interaction is friction.
Influence of solved problems of movement on models of friction is shown.
Anatomic features of a brush of a hand allow to provide on the one hand contact
to a shell during performance of sports exercise on a crossbeam in sports
gymnastics, and on the other hand in addition to compress a support without
dependence from the requirement of power short circuit of basic cinematic pair.
Settlement models for both cases are given. The third case is the sum of two
first, considering preservation of contact in movement and possible additional
all-round compression of a support.
Key words: modelling movement of the sportsman, biomechanical systems.
Кафедра прикладной механики
Могилевский государственный технологический институт
Поступила
в редакцию 5.12.2008.