Математическая морфология.
Электронный математический и медико-биологический
журнал. - Т. 8. -
Вып. 1. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTМ
http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/TITL-21.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-21-html/cont.htm
удк
537.1
Принцип ферма в проблеме пастера и левых средах
Ó 2009 г. Тукембаев Ч. А.
В работе доказано, что сущность левой среды, в частности,
метаматериала является копией левого изомера в хиральности. Три теоремы и следствие
объясняют, что левые среды определяются элементами левого-l
кручения, а не отрицательными значениями диэлектрической и магнитной
проницаемостей, как в гипотетической среде Веселаго. Вызвано необходимостью
обеспечения невидимости метаматериала в поле радара и решается заданием
элементов l-кручения в конструкции метаматериала. Гипотеза
Веселаго ошибочная, так как не удовлетворяет законам сохранения энергии и
момента импульса. Левые среды идентичны левым элементам в математике, химии,
биологии и, главное, в проблеме Пастера. Неотъемлемым свойством левой среды
является асимметрия, которая определяется отрицательной кривизной или кручением
в пространстве. Элементы длины l-кручения обладают
свойствами плазмы, как в физических, так и в биологических объектах.
Ключевые слова: хиральность, левые среды, отрицательный элемент
объема, метаматериал, отрицательная рефракция.
Введение
Отрицательный коэффициент преломления
света (рефракция) n2 приобрел
особый статус в связи с левыми средами [1-8], которые необходимо связывать с
асимметрией природы, проблемой Пастера или хиральности, так как это
краеугольный камень в естествознании [9-11]. Требует объяснения: почему живые
существа состоят из L-аминокислот и D-углеводов, а объекты неживой природы – из D-аминокислот и L-углеводов. В оптике проблема обособилась в оптическую
активность: вращение плоскости поляризации света вправо-d или влево-l,
соответственно чему имеем D- или L-изомер, т.е. выделилась в изучение стереоизомеров[1]
[12, 13]. В химии и биологии это зеркальные изомеры, а также оптически
неактивные R-изомеры [9-13]. В [13] доказано,
что в рассматриваемой среде плоскость поляризации поворачивается влево,
согласно левой молекулярной спирали, и вправо, – согласно правой спирали.
Особенностью данных проблем следует считать поведение на границе раздела двух
сред, в критической точке [12]. Накопление хирального избытка в критической
точке под действием сильного поля Ландау изучалось в [11], но прекратилось
после критики [9]. Для теоретической физики проблема Пастера, пока, неразрешима[2]
[14]: не объясняет левые и правые изомеры, в чем противоречит химии, биологии, механике и математике, аппарат
которой дает возможность решения. В этой связи суть создания метаматериала [2]
заключается в том, что впервые по нанотехнологии синтезирована левая среда с
отрицательной рефракцией; она содержит резонаторы в наноразмерах [8].
Противоречие состоит в том, что
существование левого, т.е. отрицательного[3]
элемента объема dV<0 в физике не принято. Практически всем физическим
величинам разрешили быть отрицательными, кроме элемента объема. Без внимания
осталось замечание В.Л. Гинзбурга о нецелесообразности отрицательной массы, так
как не соблюдается закон сохранения энергии [15, c.142]. Когда стали считать отрицательными
диэлектрическую e и магнитную m проницаемости среды, чтобы, тем самым, объяснить n2<0 в левых средах Веселаго [1-8], то появились
трудности объяснения отрицательной групповой скорости. Однако, периодически
неоднородные среды на спектральных интервалах, в которых групповая скорость
меньше нуля, нельзя обосновывать значениями e и m меньше нуля, так как оперирование эффективными показателями
преломления обременено риском потери для оптики новых, интереснейших и
необычных свойств среды [6]. Физики США [2], приняв за основу гипотезу Веселаго
[1], допустили ошибку[4],
так как пренебрегли зависимостью e и m от плотности r=m/V, ее производных r¢ и r² в пондеромоторных силах [16, cc. 128, 315] и, особенно, не инвариантностью вторых
производных.
Законы сохранения в физике связаны с
именем Нильса Бора, который отстоял законы сохранения импульса и энергии, как первые
физические принципы. Вместе с ними сохранение момента импульса определяет
вращение, согласно собственной ориентации или спину. Поэтому ±dV имеет
место, пока существует спин. В квантовой физике закон сохранения момента
импульса связан с ориентацией частиц и фундаментальными топологическими явлениями
– фазой Берри и оптическим эффектом Магнуса, позволяющих различать d- и l-поляризацию
и групповые скорости [17]. Они зависят от ориентации элемента объема, в том числе,
в левых средах [8], где был выбран правильный путь сохранения момента импульса,
но по непонятной причине авторы вернулись к гипотезе Веселаго. В целом, из-за
отсутствия понимания ориентации ±dV в
исследованиях выпадают производная по направлению, бинормаль сопутствующего
трехгранника, что приводит к неразрешимости левых сред и хиральности и словесному
толкованию отрицательной групповой скорости.
2. Теория и
методы решения
Изменение времени в пространстве всегда
больше нуля, чтобы не нарушалась причинность. Меньше нуля может быть элемент (дифференциал)
длины дуги dl между двумя соседними точками, где dl2=dx2+dy2+dz2. Тогда
положительным дугам соответствует пространство с положительной кривизной K>0, но
отрицательным дугам – пространство с отрицательной кривизной K<0, когда
проецируем на плоскость, поэтому знак дуги определяется параметром – кривизной.
Примером служат двояковыпуклая и двояковогнутая линзы. Прикосновению
поверхностей двояковогнутой линзы соответствует особая точка соприкосновения на
плоскости. Далее могут появиться и другие особые точки (самопересечения),
исследование которых вызывает трудности. В трехмерном пространстве (x, y, z) используют
другое определение, по Френе, и согласно формулам Френе кривизну заменяют
кручением, а кривизна берется по абсолютной величине. Поэтому, теперь, dl имеет
знак минус, если кручение t<0, поэтому отрицательные элементы длины будем называть элементами
левого-l кручения. Элемент объема ±dV – это ориентированный объем элементарного
параллелепипеда. Знак dV предусматривает выполнение закона сохранения момента
импульса. Знак ориентации ±dV
определяется спином, магнитными моментами изотопов, образующих молекулу, до тех
пор, пока не наступит фазовый переход 1 рода. В состоянии газа расстояние между
изотопами молекулы и молекулами столь велико, что молекулы подчиняются
распределению Максвелла, а потому знак ориентации не существенный. Тем не
менее, о состоянии газа мы можем судить по нормальному содержанию изотопов химического
элемента [19]. В конденсированном состоянии образование молекул зависит от направлений
спина и магнитных моментов изотопов. В этом состоянии проявляется фаза Берри,
оптическая активность молекул, и определяющее значение приобретает знак ориентации
±dV.
В настоящей работе сосредоточимся на
определении силы, обратной решетке и линии особых точек термодинамических величин
[12, cc. 59, 492, 319] на основе решения в особых точках [20,
21]. Чтобы гипотетическая среда Веселаго [1] с e,m=–1 стала теорией, нужна реформа законов физики:
Кулона, Ампера и Био-Савара-Лапласа. Эта среда, как левая среда, принята в [2]
для объяснения n2<0 в
метаматериалах из-за пренебрежения топологией. Однако у физиков сложилось
понимание существования левых сред, причем, это понимание пришло в обход
асимметрии. Казалось бы, последовательность принятия ряда физических величин с
отрицательным знаком приведет (через отрицание) к признанию левого элемента
объема с учетом его отрицательности. Осталось остановиться на отрицательном
элементе объема, так как научные принципы требуют всестороннего изучения
проблемы. Это было предпринято в [20], где математически обоснованно введен
отрицательный элемент объема [18] в связи с проблемой фазовых переходов [22].
Независимыми переменными в
термодинамических неравенствах Ландау являются приращения энтропии dS и объема dV [12, c. 81-84], а в растворах к этим переменным добавляется
дифференциал по числу частиц [12, c.
353-357]. Пригожин опирался в своих выводах на то, что отдельные члены скорости
возникновения энтропии на единицу объема в химических реакциях могут быть
отрицательными, но в сумме все члены больше нуля. В этом работа [20],
аналогична теории Пригожина, так как левые элементы объема составляют малую
часть общего числа элементов объема вблизи поверхности с отрицательной кривизной.
Рассмотрим обратную решетку по
определению [18]. Периоды решетки b1=(a2´a3)/dV, b2=(a3´a1)/dV и b3=(a1´a2)/dV. Векторные произведения (a1´a2) и т.д. равны площадям трех граней элементарного
параллелепипеда, элемент объема которого dV=[a1a2a3] – это смешанное
произведение данных векторов. Период решетки отрицательный, если грани вогнутые,
т.е. K<0, а когда вещество содержит и левый, и правый
изомер, то жидкость не имеет центра симметрии
[12, c. 479]. Так как изомеры различной
ориентации, то в малых, локальных областях вблизи поверхности с K<0
получаем мнимое изображение объекта. Это значит, что наблюдается
зеркально-асимметричный объект – двояковогнутая линза внутри правой среды, но
сама линза – реальный объект. Обозначив dV<0 в виде dV¢, обнаруживаем, что производная ¶2E/¶V2 в
термодинамических неравенствах Ландау (см. 21,2 в [12, c. 82]) должна быть смешанной производной. Тогда ¶2E/¶V¶V¢¹¶2E/¶V¢¶V и ¶2E/¶V¢¶S¹¶2E/¶S¶V, что учитывается
в наших исследованиях [23-29].
Наконец, в статье Веселаго [7] была
предпринята попытка теоретического обоснования гипотетической среды Веселаго на
основе принципа Ферма. Данное толкование поставило вариационный принцип в один
ряд с пренебрежением первых физических принципов. С учетом разъяснений сути
левых сред [5, 6] стало окончательно ясно, что причина заключена в отрицании левого
элемента объема. Поэтому в [21] доказаны три теоремы о строгой положительности e и m в любых средах на основе закона Ампера, которые приведены ниже. При
этом, левая среда определяется не e и m, а элементом dl левого кручения, которому принадлежит знак минус.
Отрицательный элемент объема, в свою очередь, однозначен элементу dl левого
кручения и в векторном элементе площади ds=dV/dl зависит от выбора знака минус в элементе dl, где dl-1=b. Поэтому "K>0 ds>0, но "K<0 ds<0.
В физике ограничиваются решением
обыкновенного дифференциального уравнения (ОДУ) 2 порядка с постоянными коэффициентами.
Это решение справедливо в отношении сохранения импульса. Согласно сохранению
энергии надо найти потерянное решение. Для этого достаточно искать его в виде
квадрата скорости – v2, так как
закон сохранения массы в таких случаях выполнен [21]. Так было найдено
аналитическое решение многочастотного резонанса в [20], где резонансы
определены собственными волновыми векторами k путем решения нелинейного ОДУ 2 порядка типа Абеля.
Фазовая скорость v2=¶p/¶r для жидкости и газа, v2=G/r для твердого тела, G – модуль сдвига, p – давление. Для ЭМ-волны v2=с2/n, где n2=em, но в пондеромоторных силах дифференцирование e и m по r приводит к производной
по направлению [16], поворот которой в обратную сторону меняет знак групповой
скорости.
Боковая волна это наблюдаемое явление
отрицательной рефракции. Исследования боковой волны электромагнитного типа
изложены в обзоре [20]. Ее применение в Красноярской РЛС и в ХААРП (HAARP) на Аляске дано в открытой публикации [30]. Найденное
решение многочастотного резонанса – это теоретическое обоснование
кроссмодуляции – люксембург-горьковского эффекта, изучавшегося Гинзбургом,
эффекта Гетманцева [30], акустического аналога кроссмодуляции [31],
структурно-неоднородных сред [32, 33] и резонанса в периодически неоднородных
структурах [6].
Боковой волне была посвящена статья [34]
и один параграф в [35]. Она образуется в ионосфере, как в многокомпонентной
плазме. Исследования боковой волны связаны с комплексностью волнового вектора,
т.е. второй вязкости, которой в i-компонентной плазме соответствует i-волновых
векторов [35]. Своевременно с публикацией [30] на открытую полку МГУ поступила
монография [36], где еще в 1973 г. были изучены свойства боковой волны, как каустики
– огибающей. Это стало подсказкой сути появления i-волновых векторов в структурно-неоднородных
(периодических) средах, и было получено решение для i-компонентной среды [37]. Наконец, решение задачи
кроссмодуляции и обобщение закона Ампера на случай 2i-проводников [21] позволило понять принципы управления
резонансом на заданной гармонике с
помощью возбуждения соседней гармоники. Найдена ошибка в определении
структурной нелинейности через нелинейные модули упругости III порядка Ландау [32, 33]: уравнения гидродинамики
связаны тензором напряжения, а не тензором деформации. Ошибка внесена в [33] из
более ранней работы [32]. Следовательно, структурную нелинейность надо
определять сжимаемостью, а не упругостью, а потому в [20, 21] выведены модули
сжимаемости III порядка, по аналогии с
модулями упругости Ландау для устранения указанной ошибки. Некорректность
следует из не инвариантности второй производной, которая и обусловила трудности
определения нелинейной длины и римановой волны как функции от классической
длины волны l=2p/k [33].
3.
Результаты и их обсуждение
Исследование боковой волны, особенно ее
каустики, дало возможность обобщить ее с левой средой: боковая волна и отрицательный
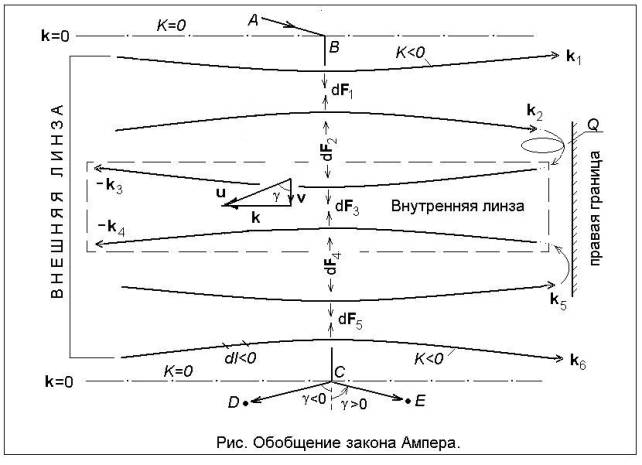
коэффициент преломления света отличаются порядком расстояния (см. рис.), так
как путь ABCD боковой волны соответствует n2<0. Согласно 6 собственным волновым векторам kj (j=1, …, 6, плюс 2 прямые k=0) кроссмодуляции, для изучения левых сред в [21] был
обобщен закон Ампера на вложенные внутрь пары k1 и k6 векторы k2, k3, k4 и k5, которые есть решение многочастотного резонанса на
высших гармониках – каустика [20]. Каждой паре kj
соответствует ri –
компонента плотности, i=1, 2, 3; j=2i [37]. Поясним геометрию и физические процессы в такой
системе.
Векторы k1 и k6 образуют внешнюю двояковогнутую линзу, поскольку
векторы k1, k2 и k5, k6 направлены в одну сторону. Поэтому проводники каждой
из пар k1, k2 или k5, k6 притягиваются силой Ампера F1 или F5. Векторы
–k3 и –k4, также, направлены в одну сторону, но притягиваются
силой F3. Между
парами разнонаправленных векторов k2, –k3 и –k4, k5 действуют силы отталкивания F2 и F4. В этой
связи, векторы k3 и k4 обособлены от внешней линзы и образуют внутреннюю
двояковогнутую линзу. Проводники k2 и k5 натягиваются, как струны, при росте силы тока I в
проводниках k1, k6 и –k3, –k4. Векторам k3 и k4 соответствуют обратные волны, когда "(-dV) k2<0, так как в среде находятся левые элементы
объема, чувствительные к колебаниям. Комплексные векторы k3 и k4 имеют
действительные части меньше нуля, и при резонансе наступает кроссмодуляция на
частоте w3,
соответствующей k3. Она
обусловлена натяжением проводников, а потому колебания низкой частоты на
внешних проводниках k1 и k6
преобразуются в колебания высокой частоты на проводниках k2 и k5,
вложенных в k1 и k6, а затем и на проводниках k3 и k4. Притяжение проводников k1, k6 и k3, k4 сообщает кривизну K<0, dl<0 обеим двояковогнутым линзам. Кривизна волновых
векторов k=0 равна нулю. Значит, кривизна среды, как собственное
значение, определяется силой Ампера, а потому знаком dl. Сейчас, лучшие
метаматериалы – это уже двояковогнутая линза [3] и многослойная среда [4], где
используют подложку и достигнут резонанс на 2 частотах: w=1.0 и 1.2 ТГц, а это следует из теории [21].
После отражения k2 и k5 от
правой границы сумма k3 и k4 равна k. Поэтому получаем вычитание векторов v-k=u, а когда u<0, то получаем левую среду или боковую волну. Падение
v вызвано поглощением среды на пути от B до
внутренней линзы в проводниках k1 и k2. Путь преломленной или боковой волны ABCD в
точку наблюдения D под углом g<0 дает преломление n2<0. В
правой среде боковой волны нет, так как k>0, а потому n2>0 и
вектор v+k=u>0 направлен в точку наблюдения E под углом g>0. В правой среде групповая скорость u есть
сложение v и k, но в левой среде – их вычитание, когда v<k.
Ошибка [7], внесенная в принцип Ферма,
заключается в следующем. Путь ABCE это кратчайшая траектория (рис.) сквозь правую среду,
где e и m > 0. Для левых сред получается максимум, но надо
не забывать, что для боковой волны скорость во второй среде больше, чем во
внешней (первой) среде на частоте резонанса, т.е. в таком спектральном
интервале, в котором групповая скорость u<0 [6]. Для боковой волны и поляритонов с u<0
кратчайшей траекторией на плоскости будет путь ABCD, если он проходит сквозь среду, состоящую из
элементов dV<0. В [1-8] принято, что
в левой среде e и m меньше нуля. Однако и
без такого предположения, левая среда потому и левая среда, потому что кривизна
K<0,
что доказано в [21] следующими теоремами.
ТЕОРЕМА 1. В левой среде e меньше нуля только потому, что элемент расстояния dl<0
определяет левую систему координат.
ДОКАЗАТЕЛЬСТВО. Для рассматриваемых сред
F=Fe,
чтобы e=FK/F не самоопределялась силой Кулона FK. Fe
сила, действующая на диполь с зарядом q=|q| и плечом l диполя.
Подставим выражения для FK и Fe в e=FK/Fe
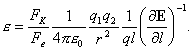
Напряженности E –электрического поля и H
– магнитного поля вместе с
волновым вектором k определяет ортогональную тройку E, H, k среды
Веселаго [1-8], которая является правой (средой) тройкой, если e, m > 0, но левой (средой) тройкой, – если e, m < 0. Из формулы следует, что e однозначно знаку элемента расстояния ±dl:
знак определяет направление силы, а dl=0 отделяет правую систему координат от левой системы.
Иных переменных, обуславливающих инверсию нет, а пондеромоторные силы в другом
виде [16] приводят к тому же результату, так как выражаются через градиент.
Докажем, что и знак вектора k зависит от
знака элемента ±dl. Для заданной частоты w риманову волну v3 дает
дифференцирование волнового вектора: (k2)¢=(w2v-2)¢=w2v-3v¢. Так как v=w/k, то, дифференцируя v по параметру t, получаем v¢ºu, т.е. групповую скорость u=dw/dk. Вторая
производная (k2)²=2k2v²/v-6k2(v¢/v)2 зависит от разности, может быть отрицательной,
положительной или равной нулю в точке инверсии, поэтому меняет знак производная
по направлению. Поскольку v=dl/dt, v¢=d2l/dt2 –
ускорение, то v²=d3l/dt3 это есть реакция среды или излучения. Она вызывает
перемену знака и эффект Террела [38, c. 296].
Излучение попадает на объект с тыльной стороны и подсвечивается тем сильнее, чем
больше реакция излучения. Наблюдение объект с тыла представляет изображение
объекта отрицательной рефракцией или вращением плоскости поляризации света.
Таким образом, и знаки ±k, и знаки ±u имеют тот
же знак, что и знак элемента ±dl. Теорема доказана.
Итак, реакцией среды или излучения
обусловлена инверсия и поворот вектора k. Тем самым, меняет знак производная по направлению,
что обуславливает вихри, турбулентность. Элементы объема dV<0 в ОДУ [20, 21] имеют смысл, если формулы не
содержат элементы dl в явном виде. Физика отрицательного элемента dl заключена
в том, что такое значение dl выражает свойства плазмы. Заданная частота w означает, что после измерения на этой частоте можно
последующими измерениями на других частотах обнаружить изменение частоты в
эффекте Доплера.
ТЕОРЕМА 2. Пусть dl-1=ds/dV – период
обратной решетки. Тогда в левых и поглощающих средах с дисперсией, подчиняющихся
закону Кулона
![]()
элемент расстояния dl<0, а e всегда положительная величина.
ДОКАЗАТЕЛЬСТВО. По определению e=F0/F, но здесь
сила F в среде определяется самим же законом Кулона для силы F0 в
вакууме. Найдем, при каких условиях сила
F<0. Для этого выразим F в виде механической силы [12, c. 59 и сноска на этой странице], которая
уравновешивается силой Fe [16]:
![]()
при S=const. Давлению p
соответствует ds>0, если K>0, но оно становится натяжением q [16] "K<0, для
которого векторный элемент площади ds=dVdl-1<0.
Давление p и натяжение q – это внешние воздействия, а dl, ds и dV – собственные
значения частицы или системы частиц вместе со знаком своей ориентацией, которые
задаются или подлежат определению.
В интеграле суммируем все элементы ±ds. Что
касается элементов ds=0, то им отвечает коллинеарность и несобственный
интеграл, а потому элементам dV=0 соответствует граница раздела фаз. Тогда сила Fm<0, если ds<0, т.е. когда dl<0 при натяжении линии l. Например,
dl<0
для поверхности с кривизной K<0. Поэтому элементы объема dV<0 в ОДУ [20, 21, 37] обретают смысл, если формулы
не содержат элементы dl в явном виде. Иначе получаем уравнение в частных
производных. Теорема доказана.
Равновесие пондеромоторной и
механической сил [16] приводит к e=F0/(Fm+Fe)®¥, так как (Fm+Fe)®0 обуславливает, видимо, электрический разряд. Максимального
значения в материалах e достигает в сегнетоэлектриках, которые играют главную роль в
биосенсорах учетом изотопов с дробным спином в триглицинсульфате, образующегося
из глицина.
ТЕОРЕМА 3. Пусть среда определяется
формулами Френе-Серре [18, c. 377-380].
Тогда левая среда задается элементом dl<0 с кручением t=½K-2½[l¢l²l¢²]<0 кривой l.
Доказательство. В соответствии с принципом Ферма для закона Ампера
[16] в точках преломления на отрезке BC найдем min dFA=I[dl´B], как для элементарной
силы Ампера, приравняв второй дифференциал нулю:
![]()
Независимые переменные – это элементы ±dl,
которые находим из уравнения
![]()
![]()
![]()
где берется криволинейный интеграл, r –
радиус-вектор до точки наблюдения, а замыкание интеграла вызвано силой Ампера.
Для кривых правого кручения, примером тому правая спираль, t>0 и, соответственно, dl>0. Поэтому, в точках
преломления "dl>0 имеет место минимум (принцип Ферма), поскольку
![]()
С учетом того, что вблизи критической
точки, т.е. в точке перегиба d2l=0, то
![]() (1)
(1)
Так как d2FA>0, то между парой проводников действует сила
отталкивания "dl>0. Значит, получаем двояковыпуклую
линзу с кривизной K>0 и углом g>0.
После замены dl=-dl левой
спирали соответствует максимум, если
![]()
Тогда между парой проводников действует сила
притяжения. Она образует двояковогнутую линзу (t<0 и dl<0), где K<0 дает измеряемое зеркальное отражение угла g, и получаем g<0 (см. рис.), соответственно боковой волне на
частоте резонанса. Значит, кратчайшей траектории отвечает максимум на частоте
резонанса или высших гармониках второй среды. Однако в точке перегиба d2l=0, поэтому
получаем минимум:
![]() (2)
(2)
с учетом перемены знака неравенства "<"
на ">". Тогда в точке перегиба неравенство (2) удовлетворяет
принципу Ферма. Теорема доказана.
Вблизи критической точки (перегиба) неравенства
(1) и (2) имеют одинаковый вид, но содержащийся в них знак ±dl определяется
по знаку ±g<0 в измерениях. Если F в e=F0/F задана
силой Ампера, то e и m выражаются нелинейной
обратной зависимостью от l, определяемой через интеграл
![]()
где m определяется знаком проводника l в
векторном произведении (dl(m)´r).
СЛЕДСТВИЕ. Докажем, что знак m однозначен знаку элемента dl. Так как B=m0mH, а dB
определяется законом Био-Савара-Лапласа, то нелинейная зависимость m от dl и r выражает
нелинейные свойства магнитного поля, где r – радиус-вектор до точки наблюдения. Запишем закон
Био-Савара-Лапласа с учетом того, что B=m0mH, и
преобразуем его:
![]()
![]()
![]()
где a – угол между векторами dl и r, L – длина проводника, по которому течет ток I. Получили
обратную нелинейную зависимость m от dl, определяемую последовательными приближениями метода
Ньютона к регистрируемому значению измеряемого угла g.
Задав в правой части начальные значения m и H, равные mm и Hm, и шаг Dl, получим
схему последовательного уточнения значений m и B
![]()
![]()
![]()
![]()
где m=1, 2, … . Так как первое значение m1=m0, то mm+1 никогда не будет равно m=–1, так как ±m отделены точкой экстремума, соответствующей точке
инверсии. Когда угол a измеряем в направлении максимального значения магнитной индукции B, то вектор
r направлен по нормали к dl, поэтому угол a равен p, а sin a=1. Тогда произведение m0m в B=m0mH означает
насколько B смещено относительно H. Именно этот факт обнаруживается по измерению и
только по измерению угла g, следовательно, знак H однозначен знаку dl.
Измерения в метаматериалах аналогичны
измерениям оптической активности и зависят от природы и частоты облучения вещества.
Угол вращения плоскости поляризации (ПП), равный p, соответствует max t [23-29], по разные стороны от которого правые и левые
изомеры выражают свою оптическую активность. При вращении ПП вправо предельным
будет угол p, согласно dV>0, а
при вращении влево предельным будет, также, угол p, но согласно dV<0. Когда углы равны 0 или p, то правая и левая пара прямых или знак кратчайшего
расстояния между двумя прямыми теряют смысл, так как прямые параллельны или
перпендикулярны[5] между собой.
Знак вращения ПП соответствует знаку кручения t и не может быть больше p в плоскости наблюдения (подробнее [23-29]). Поэтому
вращение ПП влево испытывает левый изомер, а этому его вынуждает собственная
ориентация dV<0.
Полученные
результаты служат отправной точкой изучения геометрии элементов dl
для обеспечения невидимости метаматериала в поле радара. Когда меняет знак
кручение или бинормаль, или производная по направлению, но поверхность и поверхностное
натяжение остаются неразрывными, а объемный интеграл теряет смысл, то получаем
одностороннюю поверхность (Мебиуса) с периодом 4pr, а не 2pr. Это дает
красное смещение отраженного сигнала в 2 раза и воспринимается как радиопомеха
на побочных частотах. Лист Мебиуса описывает поверхностную электромагнитную
волну Ценнека, которая имеет практическое значение [39] до тех пор, пока
существует отрицательная групповая скорость. В волоконной оптике вырождение
объема в лист Мебиуса означает появление помех в виде фантомов, как доказано в
[20, 21]. Линии самопересечения листа Мебиуса соответствует особая точка в
теореме 3. Односторонние поверхности служат наглядной геометрией метаматериалов,
потенциала двойного слоя [16] и спинов противоположной ориентации в виде бутылки
Клейна или улитки Паскаля. Наиболее простое решение – это линия задержки,
встроенная в точку самопересечения Q на правой границе (рис.), где можно поместить иные
элементы управления. Учет знака элемента dl и второй
и третьей производных в теореме 2 подчеркивает тонкость измерений, которой надо
придерживаться при оценке новых явлений. Метаматериал, по сути, есть набор
резонансных контуров. Сравнивая с боковой волной на частоте резонанса [20, 21],
нетрудно понять с учетом рекомендаций [6], что в метаматериале реализуется резонанс,
так как фаза смещена на угол p на выходе резонансного контура. Этим пренебрегли физики США в [2],
выбрав легкий путь обоснования метаматериала гипотезой Веселаго [1], которая,
по сути, оказалась следствием инверсии знака элемента длины. Отраженная волна
(см. рис.) в многослойной мембране дает инверсию волнового вектора на соседних
слоях, что соответствует перемене знака на листе Мебиуса или улитке Паскаля
(кардиоиде) и объясняет появление разноименных потенциалов на разных
поверхностях клетки.
Максимум (2)
указывает на резонанс в принципе Ферма, поэтому от нанотехнологий понадобиться
синтезировать элементы левого кручения в метаматериалах. Это не означает, что
правовинтовые линии надо заменить левовинтовыми линиями. Линия l-кручения,
как показывает боковая волна [20, 21], это химическое соединение в виде длинной
молекулы, обладающей свойствами плазмы, чего не позволяет определить гипотеза
Веселаго. Такие молекулы природа создала в живых существах, поэтому существует
иной путь обеспечения невидимости: создание плазменного облака вокруг тела. Для
нас же важно то, что, во-первых, минимум (2) для элементов левого кручения
реализуется в критической точке, т.е. в точке перегиба, где вторая производная
равна нулю. Во-вторых, накопление хирального избытка [11] происходит в
критической точке как разделение изотопов [25, 29], которое исполнено в
согласии с теорией для управления частицами [40].
3.1. Резонансный механизм хиральности. Для многочастотного резонанса надо найти комплексные
векторы k. Это возможно в случае, когда ¶r/¶P<0 или ¶P/¶V<0 на
изотерме Ван-дер-Ваальса, если dm<0 по числу частиц, поскольку k2=w2¶r/¶P, ¶P/¶r=v2, а
частота w – заданная величина. Так как (¶P/¶V)(¶V/¶r)=v2, ¶P/¶V=v2(dm/dV2), а dV2>0, то "¶P/¶V<0
суммарная масса Sm элемента
объема убывает на величину dm<0, так как дифференцируем по числу частиц. При
таком вычете массы Sm убывает до нуля и сравнивается с массой фотона.
Условие: k2<0, (k2)¢=-2w2v-3v¢>0,
(k2)²=2k2v²/v-6k2(v¢/v)2>0 приводит к резонансу (теорема 4 в [21]).
Здесь выбор (k2)²>0 обусловлен изучением взаимодействия элемента
объема dV<0 с элементами объема dV>0 окружающей среды (правой решетки). В режиме
резонанса происходит отдача в окружающую среду тех частиц (изотопов) элемента
объема dV<0, которые имеют дробный спин. Поэтому в
рассматриваемом элементе объема после вычета фермионов dV<0
остаются бозоны, составляющие хиральный избыток [11]. Элемент объема,
содержащий бозоны, становится теперь положительным, т.е. dV>0.
Значит, механизм хиральности достигается через резонанс и возможен на побочных
частотах. Суть хиральности заключается в удалении из клетки изотопов, которые
имеют дробный спин, т.е. являющихся фермионами.
В крови изотопам с
дробным спином отвечает Fe-57, Mn-55, т.е. в металлах жизни ведущая роль принадлежит
изотопам и, особенно, фермионам. В оксиде азота, биологическая роль которого
освящена в обзоре [25], фермионом является тяжелый изотоп N-15, поступающий в кровь вместе с атмосферным азотом,
где его содержание равно 0.365 %. Вязкость 15N16O равна 192.85×10–7 кг/(м×сек), а вязкость 14N16O – 189.9×10–7 кг/(м×сек) при 20°С [19], поэтому тяжелый оксид азота 15NO прилипает к стенкам сосудов и внедряется внутрь
клетки. Большее значение вязкости тяжелого оксида азота обуславливает сдвиговые
напряжения. После внедрения в клетку химически активный 15NO образует с ионами хлора хлористый нитрозил 15NOCl, который поддается фотохимическому разложению под
действием митогенетических лучей и переходного излучения [26, 27]. Поэтому хлор
превращается в молекулы и выводится из организма. В свою очередь, переходное
излучение зависит от принципа Ферма (теоремы 1-3) в спектральном интервале с
отрицательной групповой скоростью, если срабатывает резонансный механизм хиральности
так, что содержание 15N в клетке
убывает и становится меньше 0.365 %.
3.2.
Молекулярные токи в многослойной мембране. В обеих петлях улитки Паскаля токи текут в одну сторону, что приводит
к их слиянию за счет силы притяжения Ампера. Однако, внутренняя петля
отталкивается от внешней петли потому, что векторы ЭМ-поля в разных петлях
направлены в противоположные стороны после того, как ЭМ-волна проходит линию
самопересечения в узловой точке. Для молекулярного тока в разных петлях станут
антипаралелльными спины в квантовом состоянии l¹0, что обуславливает взаимодействие между разными
петлями. Это демонстрирует движение по внутренней петле улитки Паскаля с
отрицательной групповой скоростью без отражения от границ [6]. Поскольку
решение j-кратного резонанса [20] дано для 2 частиц разной
ориентации, то оно отвечает теории бильярда [41] и модели Изинга [42]. Но в
модели Изинга оставлена только пара частиц с антипараллельными спинами. Для
2-атомной молекулы угол j=p соответствует антипараллельным магнитным моментам
атомов (разных изотопов) с проекцией на плоскость в виде лемнискаты [28]. По
сравнению с [8] представление левых среда лемнискатой включает обменное
взаимодействие в веществе и поясняется следующей схемой, в том числе, для ферромагнетиков
и памяти металлов [43].
Молекулярные токи в классической схеме текут по
окружностям [16]. В каждой окружности направление тока положительное.
Окружности помещены в цилиндр, внутри которого токи соседних атомов взаимно
компенсируются, так как направлены друг против друга. Вблизи боковой
поверхности цилиндра токи не компенсируются и обуславливают намагниченность ферромагнетика.
Однако, атомы, расположенные внутри цилиндра, не отвечают своими свойствами
молекуле ферромагнетика (l=0), так как уменьшают магнитное поле. Решение [20]
устраняет этот недостаток, поскольку траектории молекулярных токов трансформируются
из окружностей в улитку Паскаля или в другой проекции в лемнискату (l¹0, терм Lz¹0). Для ряда лемнискат (888) надвиг одной лемнискаты
на другую приводит к тому, что соответствующие любым соседним лемнискатам токи
текут в одном направлении и многократно усиливают магнитное поле. Такое же
однонаправленное течение токов соседних атомов образуется, если лемнискаты
упакованы в шахматном порядке так, что выпуклость лемнискаты входит в
вогнутость соседней лемнискаты. Это соответствует памяти металлов и квантовой
схеме молекулярных токов в ферромагнетике [16] и свойствам различных органов
организма.
Выводы
Итак, метаматериалы
зависят только от знака элемента dl. Это согласуется с опытом, поскольку знак dl отвечает
хиральности, ДНК, стереизомерам и оптической активности [9-13]. Так как
плоскость поляризации вращается по левой или правой спирали [13, 18] в силу
сохранения момента импульса, то левый или правый элемент объема единственным
образом определяет хиральность по содержащейся в элементе объема линии левого
или правого кручения. Значит, отрицательный элемент объема имеет
фундаментальной значение в теоретической физике для объяснения левых сред и,
главным образом, проблемы Пастера (см. сноску3), а найденное решение
послужит новому пониманию таких объектов как лист Мебиуса и бутылка Клейна в
связи с резонансом на побочных частотах. Таким образом, изучение левых сред
Веселаго привело к тому, что теоретическая физика сомкнулась с проблемой
Пастера, чему способствовали отрицательная рефракция в метаматериалах и работа [2], оказавшейся аналогом левого
вращения в оптической активности изомеров. Теперь, физика вынуждена
присоединиться к решению краеугольной проблемы естествознания Пастера совместно
с другими науками.
ЛИТЕРАТУРА
1.
В.Г. Веселаго, УФН 92, 517 (1967).
2. D.R. Smith, W.J. Padilla, D.C. Vier et al., Phys. Rev. Lett. 84, 4184 (2000).
3. C. Metz, Phased
array metamaterial antenna system, US Patent 6958729 (2005).
4. Y. Yuan, C. Bingham,
T. Tyler et al., Optics Express 16,
No. 13, 9746 (2008).
5.
В.М. Агранович, Ю.Н.
Гартштейн, УФН 176, 1051 (2006).
6.
С.Г. Раутиан, УФН 178,
1017 (2008).
7.
В.Г.
Веселаго, УФН 172, 1216 (2002).
8.
А.В. Иванов, А.И.
Шалыгин, А.В. Ведяев и др., Письма в ЖЭТФ 85,
694 (2007).
9.
В.А. Аветисов, В.И.
Гольданский, УФН 166, 573 (1996).
10. В.Е. Островский, Е.А. Кадышевич, УФН 177,
183 (2007).
11. D.K.
Kondepudi, G.W. Nelson, Nature 314,
438 (1985).
12. Л.Д. Ландау, Е.М. Лифшиц, Статистическая физика, Наука, Москва (1964).
13. A.V. Glazer, K. J.
Stadnicka, Appl. Cryst. 19, 108 (1986).
14. В.Л. Гинзбург, О
физике и астрофизике, Наука, Москва (1985).
15. В.Л. Гинзбург,
Теоретическая физика и астрофизика.
Дополнительные главы, Наука, Москва (1981).
16. И.Е. Тамм, Основы
теории электричества, Наука, Москва (1989).
17. К.Ю. Блиох, Ю.П. Блиох, Письма в ЖЭТФ 79, 647 (2004).
18. Н.В. Ефимов, Э.Р. Розендорн, Линейная алгебра и многомерная геометрия, Наука (1974).
19. Таблицы физических величин. Ред. И.К. Кикоин,
Атомиздат, Москва (1976).
20. Ч.А. Тукембаев, В.Н. Свиденко, Исследования по
интегро-дифференциальным уравнениям (Ин-т математики НАН КР, Илим, Бишкек),
вып. 38, 145 (2008).
21. Ч.А. Тукембаев, Там же, вып. 39, 92 (2008).
22. В.Л. Гинзбург,
УФН 174, 1240 (2004).
23. Ч.А. Тукембаев,
Гипертермия, митогенетическое излучение и зеркальные изомеры в проблеме рака //
Математическая морфология / Смоленская государственная медицинская академия, т. 6, вып. 3, (2007). URL: http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
24. Ч.А. Тукембаев,
Значение ориентированного объема для
оптической активности и фазового перехода 3 рода // Там же, вып.
4, (2007).
25. Ч.А. Тукембаев,
В. Н. Свиденко, Структурная нелинейность в изотопном механизме рака // Там же, т. 7, вып. 2 (2008).
26. Ч.А. Тукембаев,
Роль переходного излучения в фотосинтезе //
Там же, вып. 3 (2008).
27. Ч.А. Тукембаев,
Влияние
критической концентрации тяжелого азота на обобщенную восприимчивость N2O в
открытой системе термодинамики // Физико-химический анализ свойств многокомпонентных
систем (Кубанский государственный технологический ун-т), вып. V, (2007). URL: http://kubstu.ru/fh/fams
28. Ч.А. Тукембаев,
Фазовый переход при образовании солитонов
и трансформации замкнутой системы термодинамики в открытую систему // Там же.
29. Ч.А. Тукембаев Разделение зеркальных
частиц в нелинейной среде // Там же,
вып. VI, (2008).
30. В.Л. Фролов, Н.В. Бахметьева, В.В. Беликович и др., УФН 177,
330 (2007).
31. В.Ю. Зайцев, В.Е. Назаров, В.И. Таланов, УФН 176, 97 (2006).
32. Liu A.J., Nagel S.R., Nature
396, 21 (1998).
33. О.В. Руденко,
УФН 176, 77 (2006).
34. В.В. Курин,
Б.Е. Немцов, В.Я. Эйдман, УФН 147, 157 (1985).
35. Л.Д. Ландау, Е.М. Лифщиц, Гидродинамика, Наука, Москва (1988).
36. Л.М. Бреховских,
Волны в слоистых средах, Наука,
Москва (1973).
37. Ч.А. Тукембаев,
Исследования по интегро-дифференциальным уравнениям (Ин-т математики НАН КР,
Илим, Бишкек), вып. 38, 155 (2008).
38. В.Г. Левич, Курс
теоретической физики, в 2-х т., Наука, Москва (1969).
39. В.Н. Дацко, А.А. Копылов, УФН 178, 109 (2008).
40. С. Чу, УФН 169,
274 (1999).
41. А.Ю. Лоскутов, УФН
177, 986 (2007).
42. Р. Фольк, Ю. Головач, Т. Яворский, УФН 173, 175 (2003).
43. В.Д. Бучельников, А.Н. Васильев, В.В. Коледов и др.,
УФН 176, 900 (2006).
fermat's Principle in pasteur'S problem and left-handed medium
Tukembaev Ch. A.
In work it is proved, that an essence of Left-Handed
Medium, in particular, a metamaterial is a copy of
the left-hand isomer in chirality. Three
theorems and corollary explain that the left-handed mediums are determined by
elements of the left-l torsion, instead of negative values of
permittivity and permeability, as in hypothetical Veselago's environment. It is
caused by maintenance of invisibility of a metamaterial at his scanning by
radar. Elements of l-torsion
are necessary for invisibility in a design of a metamaterial. The Veselago's hypothesis erroneous as does
not satisfy to laws of conservation of energy and the angular momentum. Left-Handed
Medium identical to the left elements in the mathematician, chemistry, biology
and, the main thing, in Pasteur's problem. The integral property of the left
environment is asymmetry which is determined by negative curvature or torsion
in space. Elements of length of the left torsion
possess properties of plasma, both in physical, and in biological objects.
Keywords: chirality, Left-Handed Medium, metamaterial,
negative index of refraction, negative element of volume.
Fig. - 1, bibliography - 43 references.
Кыргызский государственный университет строительства, транспорта и архитектуры
720020, Бишкек, Кыргызстан
Kyrgyz state university of construction, transport and
architecture
Bishkek, Kyrgyzstan
Поступила в редакцию
10.03.2009.
Исправлена 22.03.2009.