Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 8. -

Вып. 3. - 2009. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/TITL-23.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/cont.htm

УДК 581.5

К ВОПРОСУ ОБ ИСПОЛЬЗОВАНИИ ГАРМОНИЧЕСКОГО АНАЛИЗА В ФЕНОГЕНЕТИЧЕСКИХ ИССЛЕДОВАНИЯХ

Ó 2009 г. Баранов С.Г., Малеев А.В.

(baranov.doc)

Обсуждается возможность использования гармонического анализа циклических фигур при описании общей билатеральной асимметрии плоских билатерально-симметричных биологических объектов. В качестве модели выбраны листовые пластины березы повислой (Betula pendula Roth.). Для сканирования данных создана компьютерная программа, рассчитывающая гармонические параметры и критерий диссимметричности, как меры отклонения формы от некоторой интегральной симметричной формы. Предложен алгоритм качественного и количественного описания формы листовой пластины. Метод может использоваться для объяснения связи между формой и различными видами билатеральной асимметрии, имеющих генетическую и фенотипическую природу.

Ключевые слова: билатеральная асимметрия (направленная, флуктуирующая асимметрия, антисимметрия), диссимметрия, гармонические колебания, анализ средовых факторов.

Введение.

В последние годы наблюдается повышенный интерес к изучению асимметрии для оценки антропогенного воздействия на биологические системы. Одна из разновидностей билатеральной асимметрии - флуктуирующая асимметрия (ФА) широко используется как проявление феногенетической изменчивости для оценки воздействия на окружающую среду (Захаров В.М.,1993 – 2003, Кряжева Н.Г., 1996, Valkama J., 2001, Васильев А.Г., 2007). Под флуктуирующей асимметрией (ФА) понимают незначительное ненаправленное отклонение от «идеальной» симметричной формы, при нормальном распределении разности величин правого и левого признаков вокруг нуля (Palmer, Strobeck, 1986). Предлагаемые индексы рассчитываются по некоторым признакам, как счётным, так и мерным. Признаки представляют собой геометрические параметры, выбор которых зачастую трудно строго определить, так как эти параметры должны, не только полно отражать морфологию изучаемого объекта, представляющего собой целостную биологическую систему в виде организма или его органа, но и, с другой стороны, быть независимыми друг от друга.

Последние работы в области билатерально-симметричной изменчивости и наследственности показали, что другие виды билатеральной асимметрии направленная асимметрия (НА) и антисимметрия (АнС)) также могут отвечать на стрессовые воздействия со стороны среды и, являясь выражением генотипических свойств, наследоваться (Moller, 2003). Следовательно, билатеральная асимметрия представляет собой комплекс наследующихся и не наследующихся видов асимметрии.

Существует немало подходов к определению величины индекса билатеральной асимметрии и ее разновидностей. Практика биотестирования показывает, что общее влияние факторов, включая и антропогенные, как правило, представляет собой влияние на биологические объекты совокупности факторов, трудно поддающихся количественной оценке. Но все-таки, наибольшей трудностью является выбор признаков для определения асимметрии. Об этом свидетельствуют многочисленные публикации, посвященные флуктуирующей асимметрии, среди представителей различных групп растений и животных (Захаров В.М., 1987, Palmer, A. R., 1992 - 1997, Van Dongen S., 2002, Lens, L., 2002 и др.). У листовых пластин растений трудно провести строгую билатеральную ось. Поэтому существует необходимость более детального объяснения общей многоосевой асимметрии, включающей все или по возможности большее количество компонентов формы.

Для преодоления этих трудностей используется комплексный морфологический анализ. Например, морфометрический (морфогеометрический) подход к форме биологического объекта используется в различных прикладных программах (Rohlf, 1996, 1999; Dryden, Mardia, 1998; Monteiro, Reis, 1999; Costa, Cesar, 2000; Pavlinov, 2001). Так, анализ билатеральной асимметрии при этом основан на учёте фактора формы зубов, костей у млекопитающих, жилкования крыльев у насекомых и т.д. и, как правило, используется для выявления генетического родства или различия между таксономическими группами (Павлинов И.Я., Микешина Н.Г., 2002, Klingenberg C.P., Baluenga M., Meyer A., 2002). Используемые при этом методы разнообразны. Часто используется построение лево- и правосторонних зеркальных отображений, минимизация расстояния между полученными левыми и правыми изображениями, построение эталонной фигуры, сравнение её с реальной. Проводят различные виды оценок билатеральной асимметрии (дисперсионные виды анализа, дискриминантный, кластерный, др.).

В настоящей работе нами предпринята попытка применения для оценки общей асимметрии критерия диссимметричности, предложенного для анализа собственной симметрии циклических молекул в органической кристаллохимии (Малеев А.В. и др.,1995 - 1996) .

Выделяя на контуре биологического объекта, например, листовой пластины, ряд ключевых точек, можно охарактеризовать форму листа некоторым многоугольником (рис.1), вершины которого (ключевые точки в полярной системе координат) описываются двумя координатами R_j и φ_j. Разложение в гармонический ряд функции R_j дает постоянную составляющую р₀, амплитуды р_m , и фазовые углы δ_m, которые были названы параметрами выпуклости цикла. Особым образом выбранное положение начала координат приводит к исключению из гармонического разложения первой гармоники, поэтому m = 2,3…., (N – 1)/2, если число вершин в многоугольнике N нечетно, и m = 2,3,…., N /2, если число вершин четно.

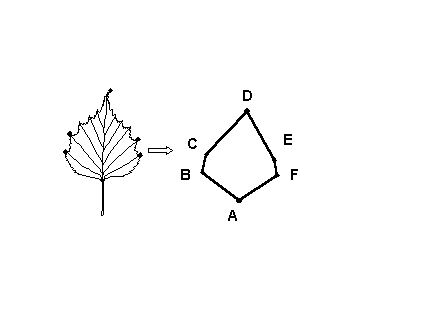
Рис.1. Построение цикла, отражающего форму листовой пластины

Кроме того, в случае четного N у последней гармоники фазовый угол δ_N_/2не определен. Аналогично коэффициенты гармонического разложения t_m и ω_m функции D_j= R_j(φ_j - 2π (j –1 )/N), были названы параметрами неравномерности ( m = 1, 2,3,…, (N – 1)/2 для нечетных N, и m = 1, 2, 3,… N/2 для четных N; в случае четного N ω_N_/2 не определен). Особым выбором направления полярной оси добиваются исключения из гармонического разложения постоянной составляющей. Параметры выпуклости и неравномерности однозначно определяют взаимное расположение вершин плоского многоугольника, поэтому содержат полную информацию о форме многоугольника. Подробно алгоритм расчета параметров выпуклости и неравномерности представлен в работе А.В. Малеева, О.И Левиной, К.А. Потехина и др., 1995. По параметрам выпуклости и неравномерности могут быть рассчитаны критерии диссимметричности для всех элементов симметрии возможных в многоугольнике, в том числе и относительно оси, соединяющей основание и верхушку листа. Кроме того, гармонические параметры позволяют проводить качественное и количественное сравнение форм многоугольников (Малеев А.В., Потехин К.А., Стручков Ю.Т., 1995) а, значит, и форм листовых пластин. Целью работы является апробация гармонического конформационного анализа листовой пластины на предмет возможности его использования при выявлении и описании качественных и количественных отклонений формы билатерально симметричных листовых пластин от идеально симметричных.

Методы и материалы

В качестве программного обеспечения использовался комплекс программы HARPAR на языке Паскаль для ПЭВМ типа IBM PC, разработанный и используемый для конформационного анализа циклических молекул в области органической кристаллохимии. Разработанная программа предполагает анализ формы циклической фигуры. На каждой из измеренных листовых пластин было выбрано шесть точек: основание черешка, крайние точки первой и второй жилок второго порядка (слева и справа), а также вершина листа. Для более детального описания формы листа можно использовать и большее число точек. Таким образом, анализ формы листовой пластины сводится к анализу формы многоугольника с использованием гармонических параметров выпуклости и неравномерности. Гармоники неравномерности (1-я, 2-я и 3-я) описывают степень и характер отклонения точек от шести лучей, отложенных от центра цикла и образующих друг с другом угол 60º. Две гармоники выпуклости (2-я и 3-я) описывают степень и характер отклонений точек цикла от среднего расстояния до начала координат (центра многоугольника).

Результаты.

Для сравнения формы двух листовых пластин были выбраны два листа примерно одинакового размера. Для каждого из них были измерены координаты шести ключевых точек и рассчитаны гармонические параметры полученных циклов (Рис.1).

Анализ этих параметров показывает, что наиболее существенное различие в форму циклов вносят первые гармоники неравномерности. Несмотря на не сильно отличающиеся амплитуды гармоник t₁ = 0,84 см для первого листа и t₁ = 0,92 cм для второго, эти гармоники значительно отличаются по фазовым углам ω₁=109º для первого и ω₁= 262º для второго. Это отражает тот факт, что в первом листе имеется тенденция к некоторому сближению точек 6,1,2 и удалению точек 3,4,5 по циклу, а во втором листе наоборот, сближены точки 3,4,5, а удалены 6,1,2 (Рис.2).

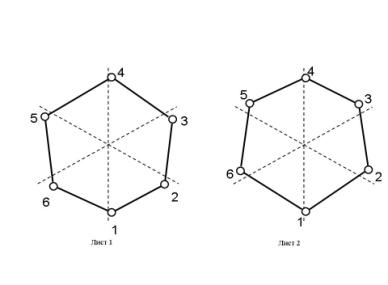
Рис.2. Первые гармоники неравномерности

Среднеквадратичное отклонение этих гармоник составляет 0,70 см. Заметно отличаются вторые гармоники выпуклости. При почти одинаковом среднеквадратичном отклонении соответствующих точек в этих гармониках, фазовом угле δ₂ = 0 для первого листа и δ₂ = 358º для второго, большая амплитуда р₂ = 1,09 см для второго листа по сравнению с р₂= 0,67 для первого, отражает большую вытянутость второго листа вдоль оси 1- 4 (Рис. 3).

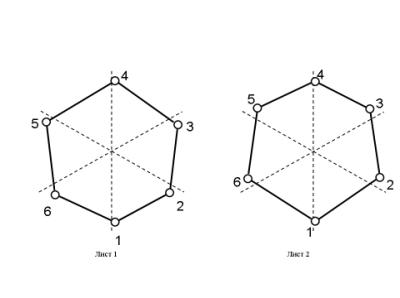
Рис.3. Вторые гармоники выпуклости

Среднеквадратичное отклонение этих гармоник составляет 0,17 см. Примерно такое же среднеквадратичное отклонение имеют и третьи гармоники выпуклости, что отражает тот факт, что в первом листе точки 1,2,3,5 имеют тенденцию к некоторому приближению к центру цикла, а точки 2,4,6 к удалению от него (рис.4).

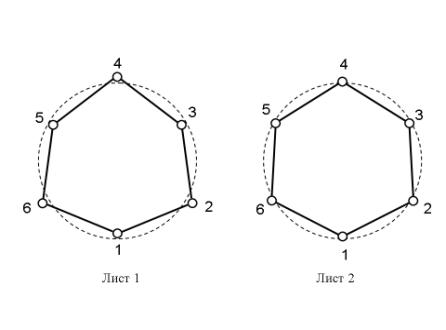
Рис.4. Третьи гармоники выпуклости

Несмотря на самые большие амплитуды вторых гармоник неравномерности t₂ = 1,85 см для первого листа и t₂= 1,97 для второго, их небольшое отличие, а также близость фазовых углов ω₂ = 270º для первого, ω₂ = 275º для второго, показывают, что эти гармоники отличаются существенно меньше (Рис. 5).

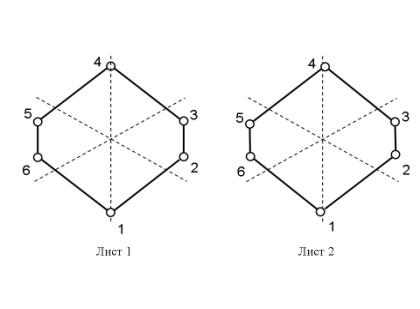
Рис.5. Вторые гармоники неравномерности

Таблица 1

Гармонические параметры двух листовых пластин, изображенных на рис. 6

Номер гармоники m	Параметры выпуклости				Параметры неравномерности
	Амплитуда p_m (см)		Фазовый угол δ_m (град.)		Амплитуда t_m (см)		Фазовый угол ω_m (град.)
	Лист 1	Лист 2	Лист 1	Лист 2	Лист 1	Лист 2	Лист 1	Лист 2
1	-	-	-	-	0.84	0.92	109	262
2	0.67	1.09	0	358	1.85	1.97	270	275
3	-0.63	-0.22	-	-	0.00	0.19	-	-

Среднеквадратичное отклонение вершин циклов этих гармоник составляет 0,09см.

Общее среднеквадратичное отклонение циклов, соответствующих сравниваемым листьям составляет 0,79 см, что свидетельствует о существенном различии форм листовых пластин (Рис. 6 и табл.1). Было проведено сравнение критерия диссимметричности и билатеральной асимметрии двух образцов листьев. Листья имели явное различие в форме. Было использовано пять билатерально-симметричных признаков, используемых для определения стабильности развития березы повислой. Значение индекса билатеральной асимметрии находилось отношением модуля разности величин правого и левого признаков к их сумме (В.М. Захаров, 2003). У первой листовой пластины наибольшее значение этого индекса имел признак – длина второй от основания жилки, а во втором листе – расстояние между основаниями первой и второй жилок. Критерий диссимметричности был выше у первого листа (1,04), чем у второго (0,55см).

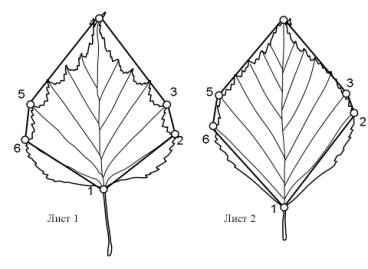
Рис.6. Внешний вид и циклы листовых пластин 1 и 2

Выводы

1. Предварительный анализ показал, что вклад неравномерности и выпуклости в диссимметрию имеет стохастический характер, т.к. расположение листовых пластин гелиочувствительных видов относительно источника освещения, также как и действие физико-химических факторов среды, микробиотических агентов серьёзно влияют на морфологические особенности пластин.

2. Предложенный метод морфометрического анализа позволяет получить интегральную характеристику общей асимметрии (в терминах кристаллографии - «диссимметричности») с учетом пространственных морфологических характеристик, следовательно, более полно дает представление об асимметрии объекта, с учётом компонента формы.

3. Методы линейного традиционного анализа билатеральной асимметрии могут быть дополнены сведениями об общей асимметрии (диссимметричности). Форма (диссимметричность) может быть объяснена различием в величине билатеральной асимметрии различных признаков. Например, в географически природо-зональных разобщенных популяциях с различной формой органов можно судить о различной степени влияния билатерально-симметричных признаков. Наиболее целесообразным мы считаем применение дискриминантного анализа, который позволяет классифицировать разные совокупности значений диссимметричности по вкладу, который вносят, входящие в них переменные (билатеральные признаки). Так же можно, используя характеристики билатеральной асимметрии (ФА, НА, АнС) классифицировать форму совокупностей (например, форму, свойственную популяциям) с учётом генотипических и фенотипических проявлений.

Литература

1. Захаров В.М. Асимметрия животных (популяционно-феногенетический подход). - М., Наука, 1987. - 216 с.

2. Захаров В.М., Чубинишвилли А.Т., Дмитриев С.Г. и др. Здоровье среды: практика оценки. Центр экологической политики, Москва, 2000.

3. Захаров В.М. Методические рекомендации по выполнению оценки качества среды по состоянию живых существ. Утв. Росэкологии от 16.10. 2003, № 460–р. М., 2003

4. Кряжева Н.Г., Чистякова Е.К., Захаров В.М. Анализ стабильности развития березы повислой в условиях химического загрязнения. Экология. 1996. N6. с. 441-444.

5. Малеев А.В., Левина О.И, Потехин К.А. и др. Гармонический конформационный анализ циклических молекул. Химия. Доклады академии наук, 1995, том 340, №4, с.449 - 504.

6. Малеев А.В., Потехин К.А., Стручков Ю.Т. Исследование диссимметричности молекулярных циклов, Химия, Доклады академии наук, 1995, том 345, №3, с.348-353.

7. Малеев А.В., Левина О.И. Сравнительный конформационный анализ двух молекулярных циклов. Кристаллография, 1996, том 41, №6, с.998 – 1005.

8. Павлинов И.Я., Микешина Н.Г. Принципы и методы геометрической морфометрии, Журнал общей биологии.2002, том.63, №6, с.473-493.

9. Васильев А.Г., Васильева И. А., Большаков В.Н. Феногенетическая изменчивость и методы ее изучения. Екатеринбург. Издательство Уральского университета, 2007.

10. Klingenberg C.P., Baluenga M., Meyer A. Shape analysis structures: quantifying variation among individuals and symmetry. Evolution 52 (10), 2002. pp.1909 – 1920.

11. Lens L., Van Dongen S., Matthysen, E. Fluctuation asymmetry as an early warning system in the critically endangered taita trush. Conservation Biology 16, 479 - 487 (2002).

12. Palmer, A. R., Strobeck C. Fluctuating asymmetry: Measurement, Analysis, Patterns. Ann.Rev.Ecol.Syst.1986.17: 391 – 421.

13. Palmer A. R., Strobeck C. Fluctuating asymmetry as a measure of developmental stability: Implications of non-normal distributions and power of statistical tests// Acta Zool. Fennica 191:57-72 Helsinki 30 June 1992.

14. Palmer A. R., Strobeck C. Fluctuating asymmetry and developmental stability: Heritability of observable variation vs. heritability of inferred cause/ Journal of Evolutionary Biology, 1997 - 10:39-49.

15. Valkama J., Kozlov M. V. Impact of climatic factors on the developmental stability of mountain birch growing in a contaminated area // J. of Appl. Ecol. — 2001. — Vol. 38. — p. 665—673.

16. Van Dongen S. The heritability of fluctuating asymmetry: a Bayesian hierarhial model .Ann. Zool. Fennici 37. 15-23, Helsinki, 14 April 2000.

TO THE USE OF HARMONIC ANALYSIS IN PHENOGENETIC STUDY

Sergey Baranov, Andrew Maleev

The possibility of the use the harmonic analysis of the cyclic figures within observes general bilateral asymmetry of the flat bilaterally-symmetrical biological object is discussed. As a model Birch (Betula pendula Roth.) leaves were chosen. The computer program scanning and calculating harmonic parameters and criteria dissymmetry as measures of the deflection of the original form in comparison to integral symmetrical form was made. The algorithm of the qualitative and quantitative description of the form of the leaves is offered. Method can use for challenge correlation among form and some types bilateral asymmetry having genetic and phenotypic origin.

Key words: bilaterally-symmetrical biological object.

Sergey Baranov*

доцент кафедры экологии и безопасности жизнедеятельности, канд. биол. наук.

Владимирский государственный гуманитарный университет.

600024, г.Владимир, пр-т Строителей, 11, Е-mail:ecobar@vtsnet.ru

*Vladimir State University for the Humanities, kafedra Ecology, natural-geographical faculty. Russia, Vladimir, 600024, pr.Stroiteley,11, 305

ecobar @ vtsnet.ru

Andrew Maleev**

доцент кафедры теоретической физики, кандидат физ.-мат. наук.

Владимирский государственный гуманитарный университет.

**Vladimir State University for the Humanities

kafedra Theoretical physics, physical-mathematical faculty

Поступила в редакцию 6.07.2009.