Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 8. -

Вып. 3. - 2009. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/TITL-23.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/cont.htm

 

 

УДК 621.391.161

 

МОДЕЛИ ЦЕЛЕЙ, ИСПОЛЬЗУЕМЫЕ В ЦИФРОВОЙ ИМИТАЦИОННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ РЛС МЕТРОВОГО ДИАПАЗОНА ДЛИН ВОЛН

 

Ó 2009 г. Панов Д. В., Юдин В. А., Мурашкин А. В.

 

(panov-1.doc)

 

Разработана методика создания моделей целей, используемых в цифровой имитационной математической модели РЛС метрового диапазона длин волн, основанная на фацетном представлении поверхности летательного аппарата и использующая компьютерную программу 3D Studio Max, что позволит получать радиолокационные характеристики различных воздушных объектов и проводить исследования новых способов обработки радиолокационной информации, повышающие эффективность работы РЛС.

Проведенные исследования поддержаны РФФИ (грант № 09-07-97519).

Ключевые слова: модели воздушных целей

 

Методики расчета характеристик вторичного излучения воздушных объектов могут быть классифицированы по методам описания поверхности аэродинамического объекта и методам расчета рассеянного электромагнитного поля.

Среди методов описания поверхности выделяют проволочные, фацетные, эллипсоидальные, простейших компонентов и др. [1]. Расчет рассеянного электромагнитного поля в сантиметровом и дециметровом диапазонах длин волн производится с использованием приближенных лучевых (методы геометрической оптики и геометрической теории дифракции) и токовых (методы физической оптики, параболического уравнения и физической теории дифракции) методов.

Основным достоинством фацетного представления поверхности летательного аппарата является отсутствие ограничений на геометрию моделируемого объекта, однако при проведении расчетов необходимы значительные вычислительные затраты. Метод простейших компонентов, напротив, при малых вычислительных затратах дает менее точное описание поверхности сложного объекта, но требует больших временных затрат для аппроксимации реальной геометрии цели простейшими геометрическими фигурами.

Необходимо отметить, что применительно к задаче исследования радиолокационных характеристик летательных аппаратов в метровом диапазоне длин волн метод простейших компонентов не пригоден из-за специфичности аналитических выражений для расчета эффективной поверхности рассеяния (ЭПР) простых тел. В метровом диапазоне длин волн не будет выполняться условие, необходимое для применения приближенных методов расчета рассеянного электромагнитного поля, а именно – размеры тела должны быть много больше длины волны зондирующего сигнала. В связи с чем, в этой области исследования наиболее предпочтительным является фацетное представление поверхности объекта.

При создании фацетной модели цели использовалась система автоматизированного проектирования 3D Studio Max. Эта система позволяет синтезировать виртуальную геометрическую модель любого сложного объекта и представлять внешнюю его поверхность в виде совокупности однотипных и пристыкованных друг к другу плоских элементов. В соответствии с фацетным представлением геометрической модели объект описывается путем задания локальных рассеивающих элементов, совокупность которых образует поверхность, а совокупность поверхностей образует объект (рис. 1). Описание локальных элементов осуществляется с использованием объектно-ориентированных структур – «треугольник», «ребро» и «точка».

 

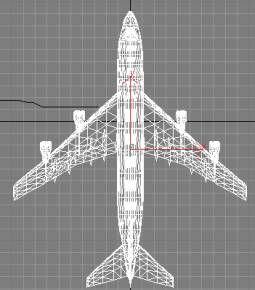
Рис. 1. Пример фацетного представления поверхности

воздушного объекта

 

Объектно-ориентированная структура «ребро», описывающая участки, находящиеся на изломах гладкой поверхности объекта, в рассмотрение не принималась, так как данные участки оказывают влияние на деполяризующие свойства цели, не проявляющиеся при измерении ее ЭПР.

Структура «точка» описывает простейший элемент, представляющий собой точку, принадлежащую поверхности объекта и являющуюся вершиной плоского треугольного элемента. Внутренними данными этой структуры являются три координаты точки в системе координат объекта.

Структура «треугольник» описывает плоскую треугольную пластину (фацет), вершины которой лежат на поверхности объекта. Элементы этой структуры – номера трех вершин треугольника в списке всех точек модели (в массиве экземпляров структур «точка») и вектор нормали к плоскости треугольника, имеющий координаты в единой системе координат объекта. Средняя точка треугольника – это экземпляр структуры «точка», образуемая пересечением трех медиан треугольника. Массив элементов структуры «треугольник» образует список всех треугольных пластин, образующих поверхность рассматриваемой геометрической модели.

Таким образом, в качестве исходной информации для работы модели, основанной на фацетном методе представления поверхности сложного объекта, используется структура «треугольник», вернее, массив, содержащий координаты вершин и номера треугольных элементов.

Фацетная модель в своем составе имеет:

модуль исходных данных (несущая частота зондирующего сигнала, возможные диапазоны наблюдения исследуемой цели и массивы, содержащие координаты вершин фацетов);

модуль определения ракурса наблюдения цели;

модуль расчета ЭПР и координат фацетов;

модуль расчета эффектов затенения.

Расчет ЭПР фацета начинается с определения координат его средней точки :

,  ,  ,

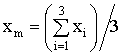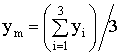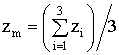где  – координаты i-ой вершины фацета.

Координаты вектора нормали  определяются из уравнения плоскости, проходящей через три точки,

.

Для определения локального рассеянного поля фацета выбирается система координат в соответствии с рис. 2. Началом локальной системы координат служит средняя точка фацета М. В качестве оси  выбирается единичный вектор нормали  к плоскости фацета. Ось  проводится из средней точки в первую из вершин фацета и определяется единичным вектором , компоненты которого определяются по выражениям

,  ,  ,

где .

Ось Z определяется векторным произведением двух векторов .
 

 

 

 

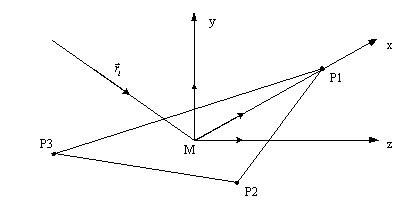
Рис. 2. Локальная система координат фацета

 

Далее координаты вершин фацета из системы координат объекта пересчитываются в локальную систему координат

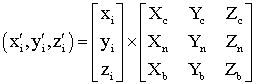
и определяется средняя точка  в системе координат фацета.

В качестве метода расчета поля рассеяния фацета используется метод физической оптики, в основе которого лежит интеграл Стреттона-Чжу. С помощью метода Гордона при решении интеграла физической оптики выражение для рассеянного поля фацета можно записать в виде [2]:

,

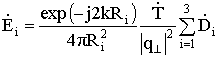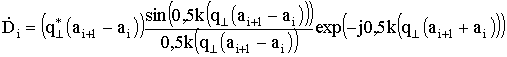, (1)

где  – волновое число падающего излучения;

*– расстояние от средней точки фацета до антенны РЛС;

– вектор, проведенный из средней точки фацета в одну из его вершин (рис. 2);  – проекция вектора распространения ЭМВ  на плоскость фацета, причем ;

 – множитель, функционально зависящий от поляризации падающей волны и электродинамических параметров фацета.

Для расчета  в выражении (1) необходимо найти векторы, проведенные из средней точки фацета в его вершины , и проекцию вектора распространения электромагнитной волны  на плоскость фацета. Вектор  в локальной системе координат имеет компоненты

,

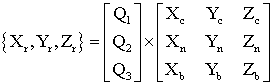где  – направляющие косинусы [3], характеризующие положение линии визирования цели в пространстве.

Проекция вектора q на плоскость фацета соответственно будет .

ЭПР локального источника вторичного излучения, образуемого одним фацетом, определяется как квадрат модуля его поля рассеяния

.

Результирующая ЭПР σ цели определяется из выражения [1]:

,

где σi(j) – ЭПР блестящей точки, образующейся в результате отражения электромагнитной волны от фацета, видимого с данного ракурса наблюдения;

f – несущая частота ЗС;

Dri(j) – смещение i(j)-ой блестящей точки вдоль линии визирования РЛС относительно первого элемента;

 B – число блестящих точек на «освещенной» поверхности цели;

  с – скорость распространения ЭМВ.

Определение видимых с определенного ракурса облучения фацетов производится путем вычисления скалярного произведения вектора нормали к плоскости фацета и вектора распространения ЭМВ. Если скалярное произведение отрицательно – принимается решение о затененности данного фацета.

Разработанная таким образом модель реальной воздушной цели несколько упрощена и адаптирована только для определения ЭПР наблюдаемой цели.

В процессе доказательства адекватности фацетной модели сравнивались результаты моделирования по средней ЭПР, распределению радиального размера, количеству и расположению наиболее интенсивных блестящих точек по корпусу планера с известными экспериментальными данными и результатами, полученными на апробированных моделях. По всем показателям, полученным на разработанной модели, результаты моделирования имеют хорошую сходимость, ошибки находятся в пределах допустимых погрешностей статических измерений.

Пример представления отражающих элементов моделей самолетов типа В-52, F-16C и F-117, основанных на фацетном методе представления поверхности, и соответствующие им диаграммы обратного вторичного излучения приведены на рис. 3–5.

В настоящее время запрограммированы описания целей следующих типов: бомбардировщики В-52, B-1, B-2, самолеты F-16C, F-117, противорадиолокационная ракета HARM, крылатая ракета Тоmahawk, управляемая ракета AGM-65, позволяющие проводить исследования эффективности различных методов распознавания классов воздушных целей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

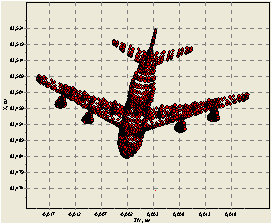
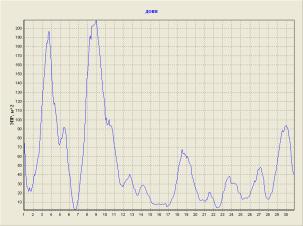
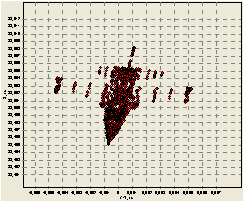
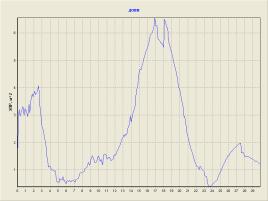
а
 

б
 
 

 


Рис. 3. Отражающие элементы модели самолета типа В-52 (а), и соответствующая ей  ДОВИ (б) (λ=1,8 м)

 

 

 

 

 

 

 

 

 

 

 

а
 

б
 
 

 


Рис. 4. Отражающие элементы модели самолета F-16C (а), и соответствующая ей ДОВИ (б) (λ=1,8 м)

 

 

 

 

 

 

 

 

 

 

 


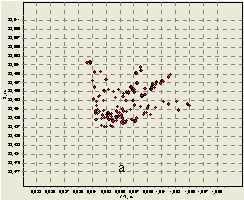
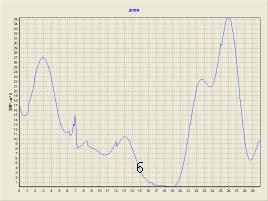
Рис. 5. Отражающие элементы модели самолета F-117 (а), и соответствующая ей ДОВИ (б) (λ=1,8 м)

 

ЛИТЕРАТУРА

 

1. Ширман Я. Д., Горшков С. А., Лещенко С. П. и др. Методы радиолокационного распознавания и их моделирование//Зарубежная радиоэлектроника. № 11, 1996. – С. 3–63.

2. Методы цифрового моделирования радиолокационных характеристик сложных объектов на фоне природных и антропогенных образований//Вопросы перспективной радиолокации. Коллективная монография. Под ред. А. В. Соколова. М.: Радиотехника, 2003. – 512 с.

3. Семин А. И. Радиолокационная математическая модель вертолета//Труды ГосНИИАС. Выпуск 1. Информационные технологии в разработках сложных систем, 1999.

 

THE MODELS OF THE PURPOSES USED IN DIGITAL IMITATING MATHEMATICAL MODEL RADAR STATION OF THE METER RANGE OF LENGTHS OF WAVES

 

Panov D.V., Yudin V. A., Murashkin A.V.

 

The technique of creation of models of the purposes used in digital imitating mathematical model radar station of a meter range of lengths of waves, based on фацетном representation of a surface of the flying device and using the computer program 3D Studio Max is developed, that will allow to receive radar-tracking characteristics of various air objects and to carry out researches of new ways of processing of the radar-tracking information, raising overall performance radar station. Carried out researches are supported by the Russian Federal Property Fund (the grant № 09-07-97519).

Кеу words: models of the air purposes.

 

Академия войсковой ПВО Вооруженных Сил РФ

им. Маршала Советского Союза А. М. Василевского, г. Смоленск

Поступила в редакцию 10.09.2009.