Математическая морфология.
Электронный математический и медико-биологический
журнал. - Т. 8. -
Вып. 3. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/TITL-23.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-23-html/cont.htm
УДК 621.391.161
МОДЕЛИ ЦЕЛЕЙ, ИСПОЛЬЗУЕМЫЕ В ЦИФРОВОЙ ИМИТАЦИОННОЙ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ РЛС ДЕЦИМЕТРОВОГО И САНТИМЕТРОВОГО ДИАПАЗОНОВ ДЛИН ВОЛН
Ó 2009 г. Панов Д. В., Юдин В. А., Караваев С. А.
Разработана методика создания моделей целей,
используемых в цифровой имитационной математической модели РЛС дециметрового и
сантиметрового диапазонов длин волн, основанная на методе простейших
компонентов представления поверхности летательного аппарата, что позволит
получать радиолокационные характеристики различных воздушных объектов и
проводить исследования новых способов обработки радиолокационной информации,
повышающие эффективность работы РЛС. Проведенные исследования поддержаны
РФФИ (грант № 09-07-97519).
Ключевые
слова: модели воздушных целей
Анализ разновидностей расчетных методов перехода от геометрии реальных целей к их радиолокационным моделям показал, что для сантиметрового и дециметрового диапазонов длин волн наиболее целесообразно использовать метод простейших компонентов [1], который при малых вычислительных затратах обеспечивает приемлемую точность описания радиолокационных характеристик целей.
При таком подходе каждый из базовых компонентов,
аппроксимирующих элементы конструкции аэродинамической цели, будет представлен
несколькими «блестящими» точками (БТ) (рассеивающими центрами (РЦ)), положение
и рассеивающие свойства которых рассчитываются аналитически.
Расчет эффективной поверхности рассеяния (ЭПР) сложных радиолокационных объектов методом простейших компонентов включает в себя три этапа:
1. Тело сложной формы разбивается на составные элементы, каждый из которых геометрически можно аппроксимировать телом простой формы (сегменты сфер или сфероидов; сегменты объектов оживальной формы или конусов; сегменты цилиндров или отрезки тонких проволок; сегменты проволочных петель; совокупности полостей; плоские пластины и клинья; разрывности), так что при этом ЭПР тела простой формы достаточно точно совпадает с ЭПР элемента реальной цели, замещаемого этим телом.
2. Для полученных на первом этапе тел простой формы, замещающих соответствующие элементы реальной цели, вычисляются значения ЭПР. Значения ЭПР каждого простого тела определяют по полуэмпирическим выражениям, полученным на основании законов геометрической оптики, физической оптики, методе краевых волн, геометрической теории дифракции.
3. На основании результатов, полученных на первом и втором этапах, находится величина ЭПР всего рассматриваемого тела. Производится суммирование ЭПР отдельных элементов (по методу случайной фазы, либо по методу относительной фазы).
На рис. 1–3 представлены модели самолетов B-52, F-16 и крылатой ракеты Tomahawk, выполненные по методу простейших компонентов.
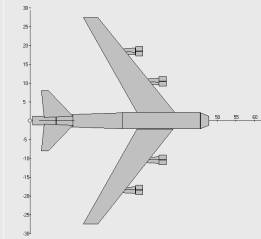
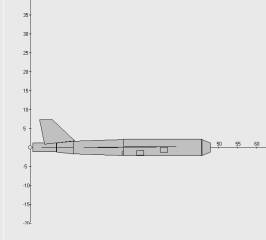
Рис. 1. Модель самолета B-52 в виде простейших компонентов
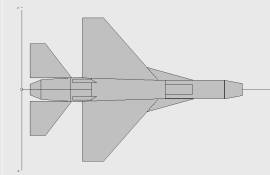
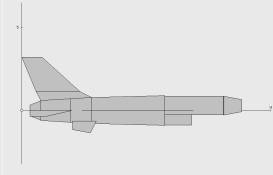
Рис. 2. Модель самолета F-16 в виде простейших компонентов
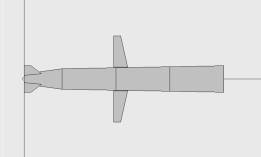
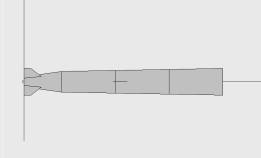
Рис. 3. Модель крылатой ракеты Tomahawk в виде простейших компонентов
Расчёт ЭПР и координат БТ аппроксимирующих тел (простейших компонентов) ведётся в системе координат, изображённой на рис. 4.
В качестве углов, определяющих ракурсы облучения цели,
выбраны курсовой угол на РЛС ![]() и угол места цели
и угол места цели ![]() .
.

Рис. 4. Обозначение осей, основных углов и точек связанной с целью системы координат
Связь между углами ![]() ,
, ![]() и углами
и углами ![]() задаётся выражением
задаётся выражением
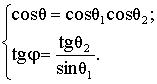 (1)
(1)
Сектора изменения углов ![]() и
и ![]() , при которых обеспечивается облучение цели вкруговую, составляют
0°
, при которых обеспечивается облучение цели вкруговую, составляют
0°![]() 360° и –90°
360° и –90°![]() 90°.
90°.
Однако в силу симметричности радиолокационной цели
(РЛЦ) относительно вертикальной плоскости, проходящей через продольную ось
самолёта, и, следовательно, в силу идентичности рассеивающих свойств левой и
правой части цели, сектор изменения угла ![]() принят
принят ![]() 180°.
180°.
ЭПР и координаты РЦ каждого из аппроксимирующих элементов определяется в пределах диапазонов ракурсов, где данный элемент даёт существенный вклад в общую ЭПР
![]()
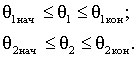 (2)
(2)
За
пределами этих диапазонов ЭПР элемента полагается равной нулю. Значения ![]() ,
, ![]() ,
, ![]() ,
, ![]() для каждого из элементов
индивидуальны и приводятся при расчёте ЭПР и координат РЦ данного элемента.
Такой порядок позволяет сократить потребные вычислительные затраты при расчёте
ЭПР и координат РЦ цели [2].
для каждого из элементов
индивидуальны и приводятся при расчёте ЭПР и координат РЦ данного элемента.
Такой порядок позволяет сократить потребные вычислительные затраты при расчёте
ЭПР и координат РЦ цели [2].
Расчёт отражений методом геометрической оптики
проводится для больших выпуклых идеально проводящих аппроксимирующих тел,
имеющих конечные главные радиусы кривизны ![]() и
и ![]() , для которых выполняется условие
, для которых выполняется условие
![]() . (3)
. (3)
Напряжённость отражённого поля в точке наблюдения вычисляется по выражению
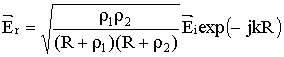 , (4)
, (4)
где ![]() – главные радиусы
кривизны фронта волны в качестве отражения (
– главные радиусы
кривизны фронта волны в качестве отражения (![]() ,
, ![]() );
);
![]() – расстояние от точки
отражения до точки наблюдения;
– расстояние от точки
отражения до точки наблюдения;
![]() – волновое число (
– волновое число (![]() );
);
![]() – напряжённость поля подающей
волны в точке отражения.
– напряжённость поля подающей
волны в точке отражения.
Задача определения ЭПР тела в рамках геометрической
оптики сводится к чисто геометрической задаче определения точки стационарной фазы,
расположенной на поверхности тела, где, в случае моностатической локации,
плоскость фронта падающей плоской волны является касательной к данной
поверхности, а также определения главных радиусов закругления в ней (![]() и
и ![]() ).
).
Пусть поверхность тела описывается выражением ![]() . Тогда в точке с координатами
. Тогда в точке с координатами ![]() вектор нормали
вектор нормали ![]() к поверхности будет
иметь координаты
к поверхности будет
иметь координаты
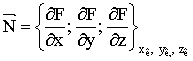 . (5)
. (5)
Для определения координат точки стационарной фазы при облучении
с ракурса ![]() ,
, ![]() надо решить систему
надо решить систему
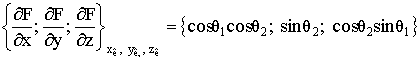 . (6)
. (6)
ЭПР точки зеркального отражения определяется по
формуле
![]() ,
(7)
,
(7)
где
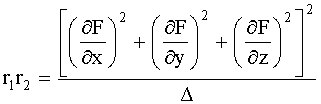 , (8)
, (8)
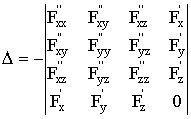 . (9)
. (9)
С помощью метода геометрической оптики могут быть рассчитаны ЭПР и координаты РЦ эллипсоида и веретена.
Уравнение эллипсоида (рис. 5) имеет вид
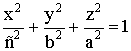 , (10)
, (10)
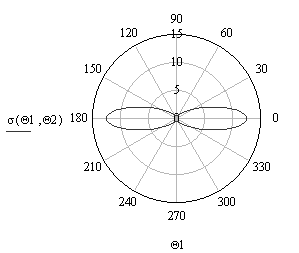
а его ЭПР (рис. 6) определяется по формуле
 ,
(11)
,
(11)
где ![]() – полуоси эллипса
соответственно вдоль осей Z,
Y, X.
– полуоси эллипса
соответственно вдоль осей Z,
Y, X.
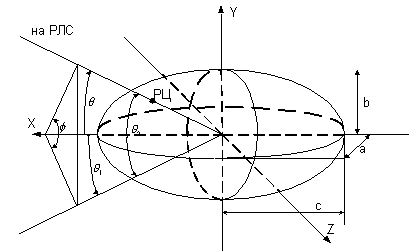
Рис. 5. Рассеяние на эллипсоиде
|
а |
б
![]() , м2
, м2
![]() , рад
, рад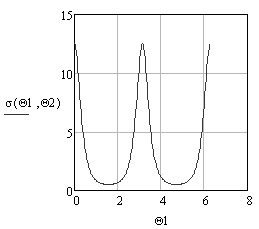
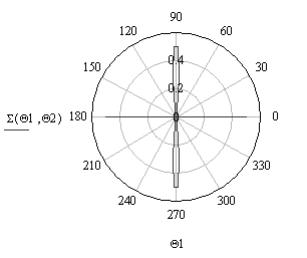
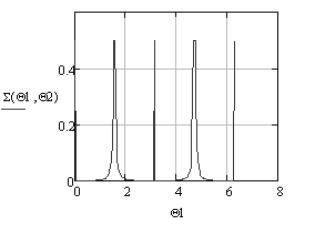
Рис. 6. ЭПР эллипсоида в полярной (а) и декартовой (б)
системах координат при а = 1 м, b
= 1 м, с = 0,5 м, λ = 0,03 м, ![]() = 0, а
= 0, а ![]() изменяется в пределах
[0, 2π] с шагом 0,01π
изменяется в пределах
[0, 2π] с шагом 0,01π
Выражение (11) строго справедливо, когда размеры эллипсоида много больше длины волны РЛС, однако его можно пользоваться и когда размеры эллипсоида сравнимы с длиной волны [2].
Координаты блестящих точек (рис. 7) находятся из соотношений
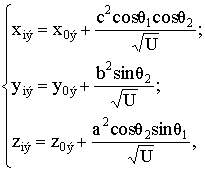 (12)
(12)
где
![]() ,
, ![]() ,
, ![]() – координаты центра
эллипсоида в связанной с целью системе координат;
– координаты центра
эллипсоида в связанной с целью системе координат;
![]() . (13)
. (13)

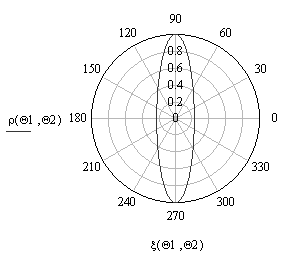
а б
Рис.
7. Индикатрисы перемещения БТ по поверхности эллипсоида в зависимости от ракурса
облучения при а = 1 м, b
= 1 м, с = 0,5 м, λ = 0,03 м, ![]() , изменяющемся в пределах [0, 2π] с шагом 0,01π,
, изменяющемся в пределах [0, 2π] с шагом 0,01π, ![]() = 0 (а),
= 0 (а), ![]() =π/4 или
=π/4 или ![]() = –π/4 (б)
= –π/4 (б)
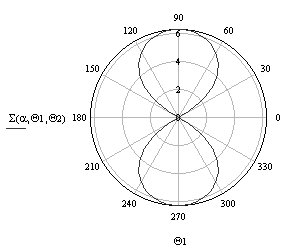
ЭПР веретена (оживала), ось которого совпадает с осью Х (рис. 8), рассчитывается по следующей формуле (рис. 9) [2]:
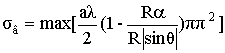 , (14)
, (14)
где
2a – диаметр миделя
веретена; ![]() – полуугол при вершине веретена;
– полуугол при вершине веретена;
![]() . (15)
. (15)
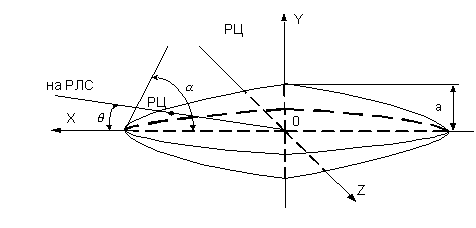
Рис. 8. Рассеяние на веретене
|
|
|
|
а б
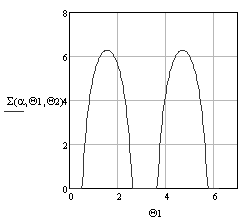
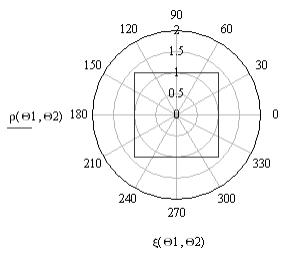
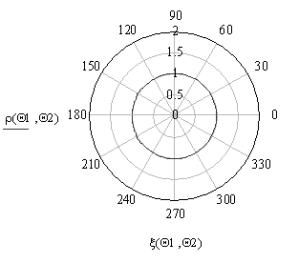
Рис. 9. ЭПР веретена (оживала) в полярной (а) и декартовой
(б) системах координат при а = 1 м, α = π/3, λ = 0,03 м, ![]() = 0, а
= 0, а ![]() изменяется в пределах
[0, 2π] с шагом 0,01π
изменяется в пределах
[0, 2π] с шагом 0,01π
Координаты рассеивающего центра веретена находятся из выражения
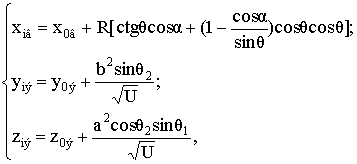 (16)
(16)
где
![]() ,
, ![]() ,
, ![]() – координаты центра
веретена в связанной с целью системе координат.
– координаты центра
веретена в связанной с целью системе координат.
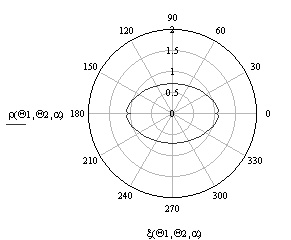
Индикатрисы перемещения блестящей точки по поверхности веретена (оживала) приведены на рис. 10.
|
|
![]() , град
, град
![]() , м
, м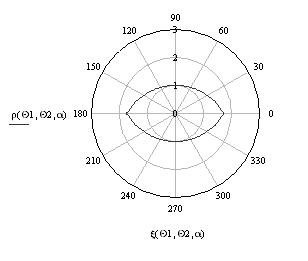
а б
Рис.
10. Индикатрисы перемещения блестящей точки по поверхности веретена (оживала) в
зависимости от ракурса облучения при а = 1 м, α= π/3, λ = 0,03
м, ![]() , изменяющемся в пределах [0, 2π] с шагом 0,01π,
, изменяющемся в пределах [0, 2π] с шагом 0,01π, ![]() = 0 (а),
= 0 (а), ![]() =π/4 или
=π/4 или ![]() = –π/4 (б)
= –π/4 (б)
Расчет отражений от тел с резкими перепадами поверхности или имеющих один или два бесконечных радиуса кривизны производится методом физической оптики.
ЭПР цилиндра длиной ![]() (рис. 11), ось
которого направлена по оси
(рис. 11), ось
которого направлена по оси ![]() , а в основании лежит эллипс, определяемый уравнением
, а в основании лежит эллипс, определяемый уравнением
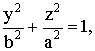 (17)
(17)
где
![]() – полуоси эллипса
соответственно вдоль осей Z
и Y, при a>>
– полуоси эллипса
соответственно вдоль осей Z
и Y, при a>>![]() , b>>
, b>>![]() , рассчитывается по формуле (рис. 12)
, рассчитывается по формуле (рис. 12)
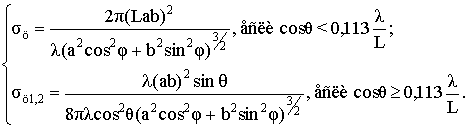 (18)
(18)
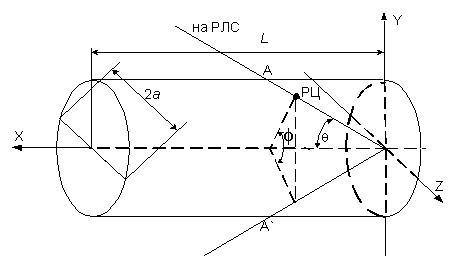
Рис. 11. Рассеяние на цилиндре
Как видно из выражения (18) при косом падении волны на образующую ЭПР цилиндра определяется двумя РЦ, расположенными на его краях.
Для кругового цилиндра выражение (18) примет вид
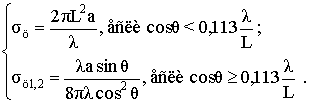 (19)
(19)
|
а |
б |
Рис.
12. ЭПР цилиндра в полярной (а) и декартовой (б) системах координат при а = 1
м, b = 2 м, L = 1 м, λ = 0,03 м, ![]() = 0, а
= 0, а ![]() изменяется в пределах
[0, 2π] с шагом 0,01π
изменяется в пределах
[0, 2π] с шагом 0,01π
При аппроксимации цилиндром средней части фюзеляжа
учитывается ЭПР его боковой поверхности при ![]()
![]() .
.
Координаты РЦ кругового цилиндра в этом случае (рис. 13) находятся из соотношений:
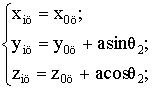 если
если ![]() (20)
(20)
где
![]() ,
, ![]() ,
, ![]() – координаты середины
дальнего от РЛС основания цилиндра;
– координаты середины
дальнего от РЛС основания цилиндра;
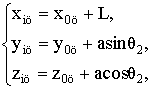 если
если ![]() (21)
(21)
|
а |
б |
Рис.
13. Индикатрисы перемещения блестящей точки по поверхности кругового
цилиндра в зависимости от ракурса
облучения при а=1 м, b=1
м, λ = 0,03 м; ![]() , изменяющемся в пределах [0, 2π] с шагом 0,01π,
, изменяющемся в пределах [0, 2π] с шагом 0,01π, ![]() = 0 (а);
= 0 (а); ![]() , изменяющемся в пределах [0, 2π] с шагом 0,01π,
, изменяющемся в пределах [0, 2π] с шагом 0,01π, ![]() = 0 (б)
= 0 (б)
При аппроксимации кромок крыльев, стабилизаторов и
киля используются круговые цилиндры, образующие которых не параллельны оси Х, а
ориентированы в пространстве в соответствии с конструкцией самолета, и, кроме
того, их радиусы не всегда удовлетворяют условию a>>![]() , b>>
, b>>![]() .
.
ЭПР усеченного кругового конуса (рис. 14) с радиусами
малого и большого оснований а1 и а2 соответственно, длиной
образующей L и осью,
совпадающей с осью Х при a>>![]() ,
, ![]() определяется из выражения
определяется из выражения
![]()
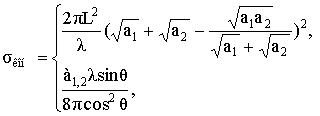
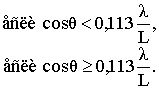 (22)
(22)
где
![]() – угол между осью усеченного
конуса и направлением локации.
– угол между осью усеченного
конуса и направлением локации.
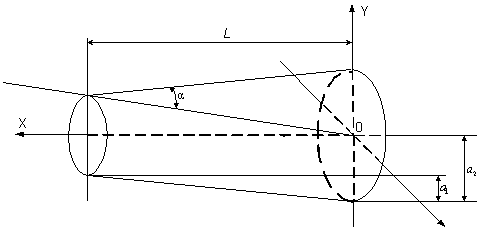
Рис. 14. Рассеяние на усеченном конусе
ЭПР полного конуса может быть получена из формулы (22) при а1=0. Координаты РЦ усеченного конуса определяется из выражений (20) и (21), где вместо угла θ используется разность (θ – α) (рис. 15).
Модель усеченного конуса позволяет решать следующие задачи: осуществить переход от реальной геометрии цели к ее математической модели при наличии радиальных участков переменного диаметра, рассчитывать характеристики вторичного излучения отдельных конусоподобных элементов, которыми представлена поверхность воздушного объекта, а также учитывать эффекты затенения.
б а
![]() , град
, град
![]() , град
, град
![]() , м2
, м2
![]() , м2
, м2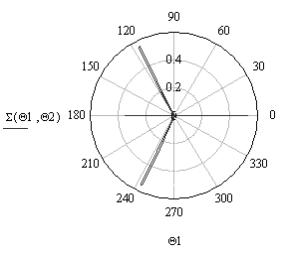
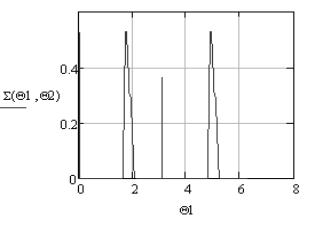
Рис.
15. ЭПР усеченного конуса в полярной (а) и декартовой (б) системах координат
при а1 = 1 м, а2 = 0,5 м, L = 10 м, λ = 0,03 м, ![]() = 0, а
= 0, а ![]() изменяется в пределах
[0;2π] с шагом 0,01π
изменяется в пределах
[0;2π] с шагом 0,01π
Тором аппроксимируются кромки круглых воздухозаборников и сопел моделируемых РЛЦ [2].
ЭПР тора (рис. 16) диаметром
2а и толщиной «губы» 2b,
нормаль которого совпадает с осью Ох при ![]() рассчитывается по
формулам
рассчитывается по
формулам
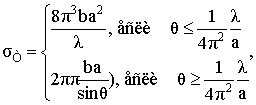 (23)
(23)
причем при ![]() отражение от
внутренней стороны тора отсутствует из-за затенения. Если в основании тора
лежит не окружность, а парабола, то вместо b в (23) необходимо подставить bЭ:
отражение от
внутренней стороны тора отсутствует из-за затенения. Если в основании тора
лежит не окружность, а парабола, то вместо b в (23) необходимо подставить bЭ:
bЭ = b/cos3![]() . (24)
. (24)
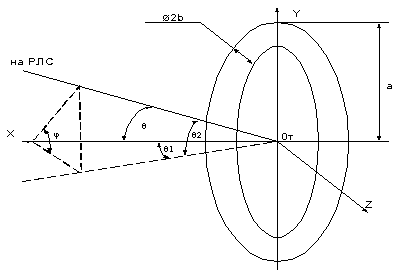
Рис. 16. Рассеяние на торе
Если b/λ<0,18, что выполняется для воздухозаборников истребителей и выхлопных сопел всех самолетов, то тор переходит в проволочную рамку, ЭПР которой рассчитывается по следующим формулам:
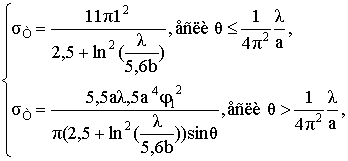 (25)
(25)
где φ1 – угол между вектором Е падающего поля и плоскостью, которая составлена направлением падения волны и нормалью к поверхности рамки.
Координаты рассеивающего центра тора или рамки в этом случае определяются из соотношений
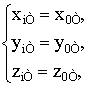 при
при ![]() . (26)
. (26)
Модель расчета ЭПР цели по методу простейших компонентов состоит из следующих модулей (рис. 17):
1. Модуль исходных данных, предназначенный для ввода характеристик планера исследуемой цели. Характеристики цели вводятся в виде формуляра, в котором указываются координаты и некоторые параметры простейших компонентов, на которые разбита данная цель. Кроме того, исходными данными являются рабочая длина волны РЛС и возможный диапазон углов наблюдения исследуемой цели.
2. Модуль определения ракурса наблюдения цели, предназначенный для расчета углового положения цели относительно приемной антенны. Выходными параметрами блока являются направляющие косинусы углов ракурса цели. Направляющие косинусы получают из матрицы перехода от сферической системы координат к прямоугольной и от прямоугольной к связанной системе координат.
3. Модуль расчета координат и ЭПР БТ, вычисляющий для аппроксимирующих поверхностей координаты и интенсивность всех блестящих точек.
4. Модуль расчета эффектов затенения, учитывающий затенение потенциальных блестящих точек аппроксимирующими поверхностями. Блестящие точки, находящиеся в области тени, из дальнейшего анализа исключаются.
Выходными параметрами модели является массив, содержащий координаты и ЭПР видимых блестящих точек цели.
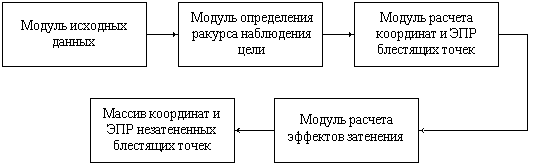
Рис. 17. Структурная схема модели радиолокационной
цели,
основанной на методе простейших компонентов
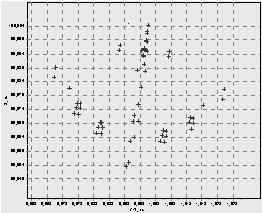
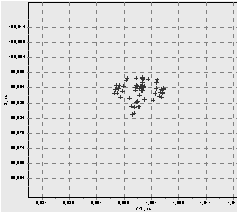
Отражающие элементы моделей самолетов В-52H, F-16C и крылатой ракеты Tomahawk приведены на рис. 18, а соответствующие им диаграммы обратного вторичного излучения (ДОВИ) – на рис. 19–21.
Известно, что ширина лепестков ДОВИ Δθ зависит от отношения линейных размеров цели L (поперечный размер) к длине волны λ, т.е. Δθ≈λ/L [3]. Для модели самолета В-52H минимальная ширина лепестка ДОВИ на боковом ракурсе составляет Δθ=0,06° (Δθ=0,0021 рад) (рис. 19), а значит L≈48 м; для модели самолета F-16C Δθ=0,2° (Δθ=0,0069 рад) (рис. 20) L≈15 м; для модели КР Tomahawk Δθ=0,6° (Δθ=0,02 рад) (рис. 21) L≈5 м.
б а
в
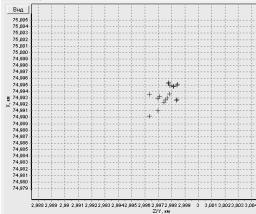
Рис. 18. Отражающие элементы моделей самолетов В-52H (а), F-16C (б) и крылатой ракеты Tomahawk (в)

Рис. 19. ДОВИ модели самолета В-52H (λ=0,1 м)
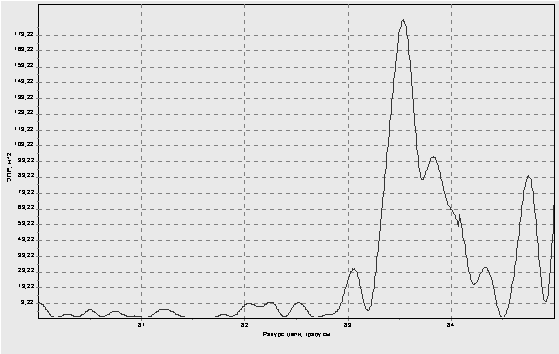
Рис. 20. ДОВИ модели самолета F-16C (λ=0,1 м)
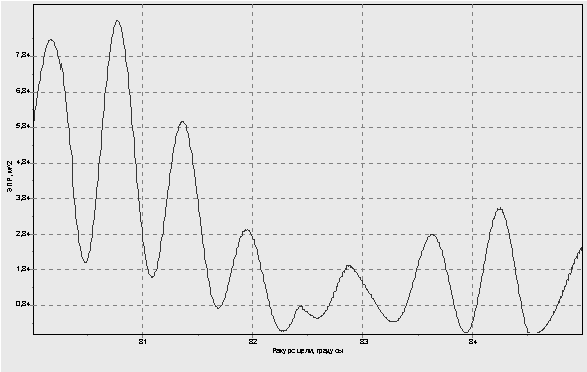
Рис. 21. ДОВИ модели КР Tomahawk (λ=0,1 м)
Таким образом, ширина лепестков полученных ДОВИ моделей целей соответствует их линейным размерам, что свидетельствует об адекватности разрабатываемых моделей целей.
ЛИТЕРАТУРА
1. Ширман Я. Д., Горшков С. А., Лещенко С. П. и др. Методы радиолокационного распознавания и их моделирование//Зарубежная радиоэлектроника 1996 г. №11. С. 3–63.
2. Радиолокационные характеристики СВКН/ Н. А. Алексеев, В. А. Белякова, Ю. А. Гращенко и др.; Под ред. Ю. И. Любимова. – ЦАГИ, 1987. – 209 с.
3. Теоретические основы радиолокации//Под ред. Ширмана Я. Д. М.: Сов. радио, 1970. – 560 с.
THE MODELS OF THE
PURPOSES USED IN DIGITAL IMITATING MATHEMATICAL MODEL RADAR STATION OF
DECIMETER AND CENTIMETRIC RANGES OF LENGTHS OF WAVES
Panov
D. V., Yudin V. A., Karavaev S. A.
The technique of creation of models
of the purposes used in digital imitating mathematical model radar station of
decimeter and centimetric ranges of lengths of waves is developed, based on a
method of the elementary components of representation of a surface of the
flying device that will allow to receive radar-tracking characteristics of
various air objects and to carry out researches of new ways of processing of
the radar-tracking information, raising overall performance radar station. Carried
out researches are supported by the Russian Federal Property Fund (the grant №
09-07-97519).
Кеу words: models
of the air purposes
Академия войсковой ПВО Вооруженных Сил РФ
им. Маршала Советского Союза А. М.
Василевского, г. Смоленск
Поступила в редакцию 10.09.2009.