Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 8. -
Вып. 4. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm
УДК
621.391.161
математическое
обоснование показателя скрытности сверхширокополосных сигналов для систем связи
различного назначения
Ó 2009 г. Иванов Д. Н., Сеньков М. А.
Представлено математическое основание применения
сигналов, энергия которых равномерно распределена в широком диапазоне частот,
для повышения скрытности систем передачи данных военного и гражданского назначения.
Ключевые слова: скрытности
сверхширокополосных сигналов.
Для военной аппаратуры
передачи данных важным свойством является скрытность, которую она может
обеспечить системе передачи данных (СПД). Высокая скрытность СПД позволяет
избежать постановки прицельных помех, препятствует вскрытию позиционных районов
и снижает вероятность перехвата информации средствами радиоэлектронной разведки.
Выбор показателя скрытности
сигнала начнём с понятного с физической точки зрения утверждения: сигнал
обладает наибольшей скрытностью, если его энергия равномерно распределена в
широком диапазоне частот, т. е. спектр сигнала равномерен в заданной полосе
частот. Если спектр сигнала равномерен, то все гармоники в спектре используются
на полную мощность, тогда противнику сложно выявить участки спектра с
повышенной (пониженной) энергией, следовательно, сложно запеленговать наличие
передачи или поставить прицельную помеху.
Спектр – это функция,
имеющая сложную закономерность, что не позволяет сравнивать между собой спектры
различных сигналов с точки зрения их равномерности. Таким образом, необходимо
решить задачу сведения функции к показателю, который достигал бы максимума в
случае, когда спектр равномерно распределён в заданной полосе частот.
Сформулируем данную задачу
следующим образом:
,
(1)
где К2 –
показатель скрытности;
– функционал преобразования функции в
показатель.
Функционал (1) представляет
собой переменную величину, значение которой зависит от вида функции,
описывающей амплитудный спектр исследуемого СШП сигнала заданной формы. Для
получения целевой функции (функционала) воспользуемся неравенством Иенсена:
,
(2)
где y = f(x)
– функция, выпуклая на некотором интервале;
х1, х2,
…, хn – произвольные числа из этого интервала;
α1, α2,
…, αn – произвольные положительные числа, сумма которых
равна единице.
Докажем,
что данное неравенство справедливо для любой выпуклой функции.
Под
выпуклой функцией f(x) (в некоторых источниках
выпуклая снизу функция) будем понимать функцию, для которой выполняется условие
(рис. 1):
f˝(x) > 0 (3)
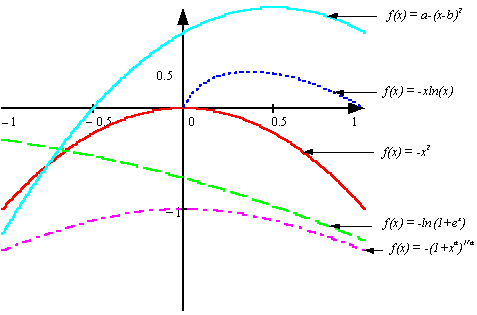
Рис. 1. Выпуклые функции.
Условимся, что функция y = f(x)
выпуклая на некотором интервале (рисунок 2), х1, х2,
…, хn – произвольные числа из этого интервала, α1,
α2, …, αn – произвольные положительные
числа, сумма которых равна единице.
Для доказательства
воспользуемся понятием полной (математической) индукции, которое формулируется
следующим образом.
Пусть А(n) –
зависящее от 
утверждение. Если
доказано, что А(1) выполняется и при условии, что А(n)
справедливо для некоторого n, верно также A(n +
1) (шаг индукции), то А(n) справедливо для всех 
.
Для n =
2 выражение (2) примет вид:
. (4)
Геометрически выражение (4)
можно представить в виде рис. 2.
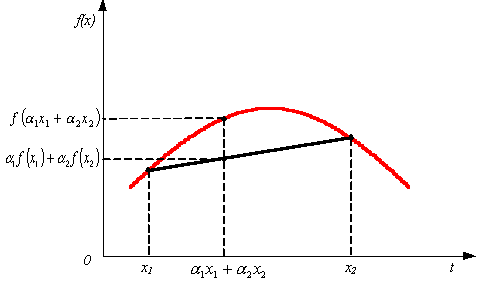
Рис. 2. Геометрический смысл
теоремы Иенсена для n = 2
Как показано на рисунке 2,
прямая, образованная точками x1, x2, лежит ниже графика функции
f(x), а значит, выполняется (2).
Зададим в качестве базы
индукции выражение (4).
Проведём индукционный
переход, для этого воспользуемся индуктивным предположением, поскольку (2)
справедливо для n = 2, значит справедливо и для n –
1, т.е. имеем
. (5)
Рассмотрим случай n –
переменных:
.
Поскольку 
, то
,
т.е.
,
тогда
;
.
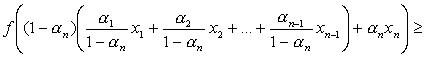
Что и требовалось доказать.
С
помощью неравенства Иенсена докажем, что выпуклая функция принимает максимальное
значение в случае равенства переменных х1, х2,
…, хn, т.е.
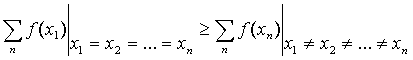. (6)
Пусть
. (7)
Т.к.
, (8)
то
. (9)
Если
(10)
и
, (11)
то
.
В качестве исходного
выражения имеем
. (12)
С учётом (9) и (10), выражение (12) примет вид
. (13)
. (14)
Из (14) следует, что при 
функция f(x) принимает максимальное значение.
Рассмотрим случай, когда
;
(15)
, (16)
тогда выражение (12) примет вид:
. (17)
С учётом (11), выражение
(17) можно записать в виде
;
.
(18)
Из выражения (2.21) видно,
что в случае, когда 
, функция f(x) может
принимать значения меньше максимального 
.
Из данного доказательства и
выражений (14) и (19) можно сделать вывод, что
.
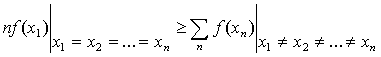А значит утверждение (6)
верно. Что и требовалось доказать.
Из проведённого
доказательства следует, что для определения степени равномерности спектра можно
использовать функционал вида (1), поскольку, когда все гармоники в спектре
сигнала буду иметь одинаковые амплитуды (случай, когда выполняется условие
(10)), функционал вида (19) примет максимальное значение.
.
(19)
где 
– выпуклая функция.
Перейдём к интегральной
форме записи неравенства Иенсена (для непрерывного спектра):
;
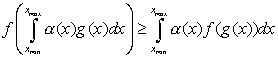(20)
(21)
где g(x) и
α(x) – функции, определённые на интервале от xmin до xmax и удовлетворяющие условию (21).
С учётом (20) показатель (19) запишем в виде
.
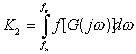(22)
Для получения показателя,
имеющего аналогию в теории информации, выберем в качестве выпуклой функцию вида
,
тогда, выражение назовём
энтропийным показателем скрытности.
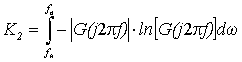(23)
Энтропией системы называется
сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей,
взятая с обратным знаком
,
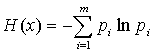где m –
число состояний системы (возможностей);
pi – вероятность i –
го состояния (возможности).
Впервые в работах Л.
Больцмана и Дж. К. Максвелла, выкладки из которых приведены в различных
публикациях по теории информации [1,2], было доказано, что энтропия имеет
максимальное значение (24), когда состояния системы (возможности) равновероятны.
. (24)
Таким
образом, имеем энтропийный показатель скрытности единичного сигнала, характеризующий
равномерность спектра кодовой последовательности в заданном диапазоне частот.
Чем более равномерен (прямоуголен) спектр кодовой последовательности в заданном
диапазоне частот, тем выше значение показателя скрытности, а значит выше скрытность
радиопередатчика.
Литература
1.
Дмитриев
В. И. Прикладная теории информации: Учебник для вузов. М.: Высшая школа, 1989.
–325с.
2.
Стратонович
Р. Л. Теория информации. М.: Советское радио, 1975. –424с.
THE
MATHEMATICAL BASIS OF THE INDEX OF THE OVERWIDEBAND SIGNAL SECRECY OF THE ANY
FUNCTIONAL COMMUNICATIONS.
Ivanov D., Senkov M.
In this article is presented the mathematical basis of
the application of the signals (the energy of which is equally arranged in the
ultra band) for the increase of the secrecy of the data transmission systems
for the military and civil purpose.
Key words: overwideband signal secrecy.
Кафедра радиотехники
Кафедра радиоэлектроники
Академия
войсковой ПВО Вооруженных Сил РФ
им. Маршала Советского Союза А. М.
Василевского, г. Смоленск
Поступила в редакцию 17.11.2009.