Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 8. -
Вып. 4. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm
УДК
621.396.969
Обработка
сигналов с большой частотой
Ó 2009 г. Крисенко Ю.Ю., Вашкевич С. А.
Статья посвящена вопросам оптимальной обработки сигналов при
использовании радиолокационных сигналов, записанных в цифровом виде.
Ключевые слова: оптимальная обработка, модуль корреляционного интеграла,
дискретная свертка.
Одним
из важных вопросов обработки радиолокационных сигналов является извлечение
полезной информации о цели.
Для
удобства преобразований радиолокационный сигнал записывался в цифровом виде с
помощью аналого-цифрового преобразователя на типовой радиолокационной станции,
использующей импульсный широкополосный сигнал с линейным частотно-модулированным
сжатием и преобразовывался в изображение (рис. 1, а, б) размером
64×3 000 отсчетов.
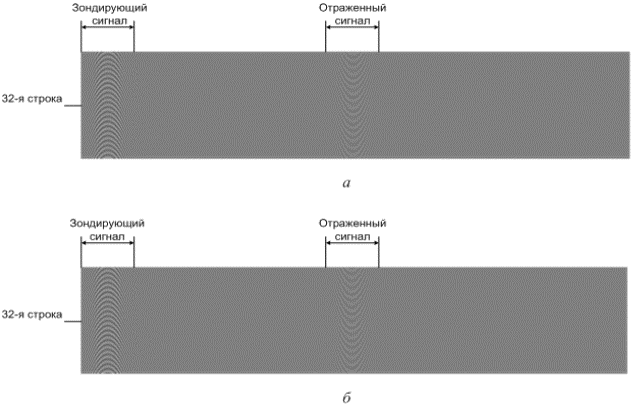
Рис. 1. Двумерное
графическое изображение синусной а и
косинусной б
составляющих зондирующего и
отраженного сигналов
Для
обработки использовалась 32-я строка изображений. Первые 300 отсчетов двумерного
изображения являются зондирующим сигналом, а именно его синусной и косинусной
составляющей.
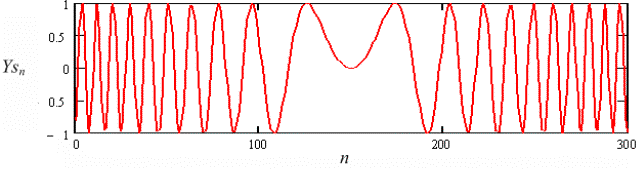
Графики этих составляющих
(зависимость амплитуды синусной составляющей сигнала Ysn и амплитуды косинусной составляющей
сигнала Ycn от отсчета n в изображении) показаны на
рис. 2, а, б.
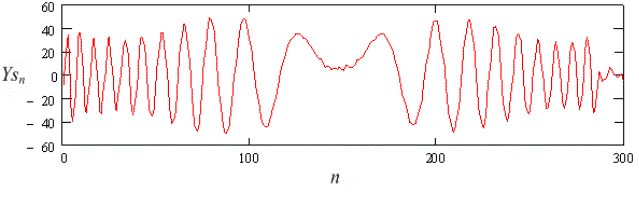
а
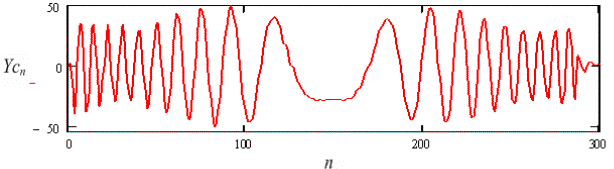
б
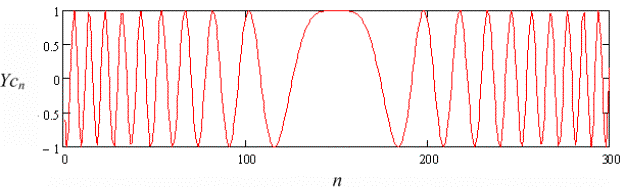
Рис. 2. Зависимость амплитуды
синусной Ysn а и
косинусной Ycn б
составляющих зондирующего
сигнала от номера отсчета в его двумерном изображении
Зондирующий
сигнал Yn в комплексной форме записывается в виде
Yn = Ycn + iYsn,
(1)
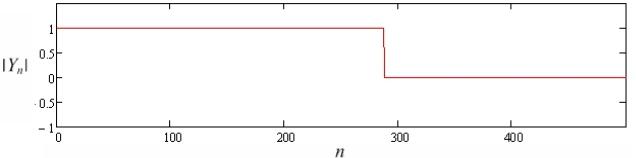
а его огибающая показана на рис. 3, где ׀Yn׀ – модуль комплексного числа.
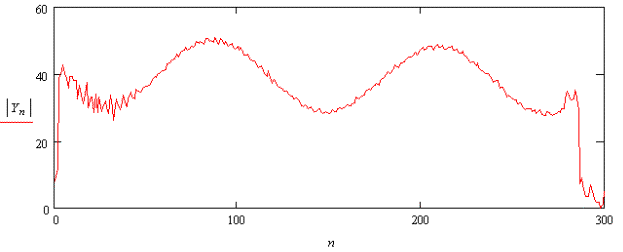
Рис. 3. Огибающая
зондирующего сигнала
Как
известно [1, 2], сущность оптимальной обработки сигнала заключается в вычислении
модуля корреляционного интеграла с последующим сравнением его с пороговым
значением. Следовательно, необходимо вычислить модуль корреляционного интеграла,
характеризующий степень связи между принятым и опорным сигналами:
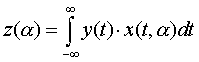 , (2)
, (2)
где x(t,α) –
зондирующий (опорный) сигнал, y(t) –
принятый.
Поскольку цифровой сигнал
является разновидностью дискретного, то для обработки изображений необходимо
вычислять не интеграл, а сумму, соответствующую дискретной свертке сигналов:
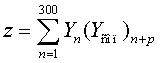 , (3)
, (3)
где Yn – значение зондирующего сигнала на n-м отсчете,
(Yсоп)n+p – комплексно сопряженное
число, соответствующее отсчету n+p,
p – текущий номер отсчета.
Таким образом, при
вычислении суммы произведений значений зондирующего сигнала на комплексно
сопряженные значения по всей шкале отсчетов получим зависимость модуля значения
дискретной свертки от номера отсчета в изображении сигнала (рис. 4).
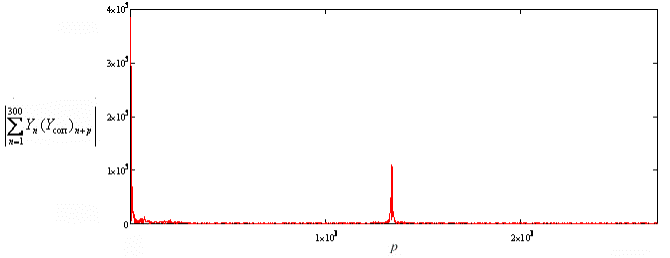
Рис. 4. Модуль дискретной
свертки 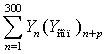
По графику можно сделать
вывод о наличии радиолокационной цели. Это видно по наличию «пика» на графике,
показывающему максимальную степень связи между зондирующим (опорным) и принятым
сигналами.
Вычислим
модуль дискретной свертки (3) для «идеального» зондирующего сигнала (рис. 5, а, б,
в).
а
б
в
Рис. 5. Синусная а и косинусная б составляющие «идеального»
зондирующего сигнала и его
огибающая в
Результат вычислений (рис.
6) значительно отличается от предыдущего, четко выраженный «пик» (рис. 4)
отсутствует.
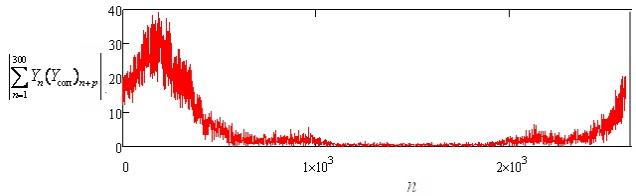
Рис. 6. Результат дискретной
свертки «идеального» зондирующего
и принятого сигналов
Можно
сделать вывод, что для оптимальной обработки радиолокационного сигнала с целью
выделения полезной информации целесообразно использовать зондирующий сигнал,
просачивающийся на вход приемной системы, что позволит повысить вероятность
правильного обнаружения цели и уменьшить значение вероятности ложной тревоги.
Литература
1. Охрименко А. Е. Основы радиолокации и радиоэлектронная
борьба. Часть 1. Основы радиолокации. М., Воениздат, 1983. 456 с.
2. Теоретические
основы радиолокации. Под ред. Я. Д. Ширмана. М., Советское радио, 1970. 560 с.
PROCESSING HIGH-FREQUENCY SIGNAL
Krisenko Y. Y., Vashkevich S. A.
The Article is dedicated to questions of the optimum processing signal
when use radar signal, recorded in digital type.
Key words: optimum processing signal.
Кафедра радиоэлектроники
Академия
войсковой ПВО Вооруженных Сил РФ
им. Маршала Советского Союза А. М. Василевского, г. Смоленск
Поступила в редакцию
2.12.2009.