Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 8. -
Вып. 4. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm
УДК
519.711.3
Применение методов
абстрактной алгебры для математического описания объектов данных на
этапах информационного моделирования Компьютерных моделей
Ó
2009 г. Маманович К. А.
В данной работе рассматривается объектно-ориентированный подход,
применяющийся в настоящее время для информационного моделирования сложных
программных комплексов. Излагается
способ математического описания и семантического представления данных,
основанный на методах абстрактной алгебры. За математическую основу выбрана алгебраическая система. Ее
применение основано на ключевом понятии объектного подхода - объединении в
единой информационной структуре
множества данных, как базовых свойств объекта и операций, выполняемых над ними,
как функций, описывающих поведение объекта в реальном мире. Такой подход
позволяет математически точно описать информационные модели, в части касающихся
абстрактных типов данных, что в свою очередь позволит выполнить верификацию
элементов полученных информационных моделей.
Ключевые слова: абстрактная алгебра,
информационное обеспечение, компьютерные модели.
В настоящее время, принципы
абстрактных типов данных (АТД), такие как инкапсуляция данных, определение
данных через операции [1-4], наследование и полиморфизм применяются в современной
методологии проектирования информационного и программного обеспечения.
Главная особенность
концепции АТД заключается в понятии типа как множества значений,
характеризуемого посредством одного набора операций. Создание значений типа
данных, а также все манипуляции ими производятся посредством операций из заданного
списка. Главным принципом построения абстрактных типов данных является достижение
независимости со значениями данного типа от их конкретного представления [3,4].
Математический подход к определению АТД формально соответствует понятию объекта,
как информационной единицы.
Формально с математической
точки зрения абстрактный тип данных определяется как многосортная алгебра
[5-7].
Семантика абстрактного типа
данных определяется с помощью алгебраической спецификации, которая представляет
собой тройку:
,
где 
- сигнатура алгебры
, а 
- конечное множество аксиом. В алгебраическом подходе
абстрагирования типы данных описываются в терминах многосортной алгебры путем
установления соответствия сортам переменных множеств значений данных. Таким
образом данный метод сводится к заданию:
имени 
определяемого типа данных;
других типов 
, необходимых для определения 
;
функций 
, определяемых на множествах значений данных 
;
областей определения и
областей значений, обозначаемых функций 
;
отношений между функциями 
, задаваемых в форме аксиом.
Операции или функции,
определяющие абстрактный тип данных имеют следующую классификацию:
1. Функции создания
(инициальные функции или первичные конструкторы) в области определения которых
нет операндов, принадлежащих определенному типу, но определяемый тип
присутствует в области значений.
2. Функции модификации
(конструкторы, или комбинированные конструкторы), имеющие определяемый тип в
области определения и в области значений.
3. Функции доступа или
анализаторы которые имеют определяемый тип в области определения, но тип 
отсутствует в области
значений.
При построении спецификации
нового типа данных на основе имеющейся системы типов необходимо, чтобы выполнялось
важнейшее свойство - достаточная полнота спецификации, то есть чтобы не
порождалось новых значений исходных типов. Если спецификация АТД недостаточно
полна, то есть не все операции в ней заданы, то несколько различных множеств
может быть замкнуто относительно этих операций.
Еще одна особенность состоит
в строгом контроле над операциями, входящими составной частью в объект при этом
обеспечивается высокую степень независимости и целостности данных.
Применение принципов
абстрактных типов данных, принципа информационной локализованности и наличие
математической спецификации в разработке информационного и программного
обеспечения систем автоматизированной разработки компьютерных моделей позволяет:
1. Использовать методы
разработки формальных спецификаций АТД и математически корректно описывать
информационные объекты САРПО. Использование алгебраических конструкций дает
возможность применения к семантическому описанию данных математических методов.
2. Совместно хранить данные
и процедуры их обработки, что позволяет повысить уровень пользовательского
интерфейса, приблизить операторы работы с данными к операциям, с которыми
привычно работать разработчику (проектировщику).
3. Позволяет локализовать
компоненты ИО и ПО, доступные к быстрым изменениям, и за счет этого облегчить
адаптацию ИО и ПО к условиям внешней среды (предметной области). Для разработки
компьютерных моделей с помощью инструментальных систем особенно важна
локализация в отдельных модулях комплекса возможных ограничений (педагогических,
эксплуатационных) для объектов проектирования. Это необходимо для настройки
системы на широкий класс объектов проектирования и адаптации к изменениям в
конструкциях и технологиях создания объектов проектирования.
4. Определение данных через
набор операций доступа и независимость от их физического представления
позволяет обеспечивать настройку на информационные структуры баз данных САРПО
за счет подключения структур баз данных в модули реализации АТД и/или
организовывать информационный интерфейс через операции АТД.
5. Принципы АТД дают
возможность создания множества взаимозаменяемых программных реализаций АТД и
позволяют достигать требуемой производительности работы с данными и знаниями
САРПО за счет многовариантности и взаимозаменяемости реализаций АТД.
6. Определение в качестве АТД
информационных объектов сложной семантики позволяет разрабатывать алгоритмы проектирования
ПО с использованием операций манипулирования данными более высокого уровня, операций,
несущих смысловую нагрузку проектирования.
7. Совместное использование
концепций типовых объектов и алгоритмов и принципов АТД позволяет отдельно
разрабатывать библиотеку типовых алгоритмов и библиотеку реализаций АТД,
определяющих информационные объекты проектирования и различающихся полнотой и
точностью отдельных операций.
8. На основе инвариантных
объектно-ориентированных операций и модулей АТД создавать компоненты
инструментальной системы, используемые при разработке компьютерных моделей
войсковой ПВО.
Однако при всех достоинствах
объектного подхода на сегодняшний день не существует (автору неизвестны работы
в этой области) методик, строго описывающих последовательность применения ОП и
принципа АТД для информационного моделирования программных систем.
После построения
концептуальной модели классов, необходимо применить семантическое описание
классов. Такой подход обеспечивает корректное представление формализуемой
информации в виде данных, и делает возможным в дальнейшем исследовать полученные
вычислительные структуры на непротиворечивость и достаточную полноту.
Для семантического
представления классов воспользуемся теорией алгебраических систем, которую
применяют также для описания семантики АТД.
Как исходное условие при построения методики необходимо принять то, что в объектном подходе класс рассматривается не только как структура с совместным хранением атрибутов и операций их обработки, но и его жизненный цикл, при котором взаимодействие с другими объектами происходит на основе реляционных моделей.
В качестве основного
математического описания объектов и классов, как базовых информационных
компонент объектного подхода будем применять конструкции абстрактной алгебры и
алгебраических систем. В [5-8] приводятся примеры применения этого подхода.
Применим понятие алгебраической системы (АС) [9,10]. АС типа 
называется объект 
, состоящий из трех множеств: некоторого непустого множества 
, множества операций 
, и множества предикатов 
, заданных на множестве 
. Исходя из свойств алгебраических систем систему 
будем считать
алгеброй, если 
, и моделью (реляционной моделью) если 
. Таким образом, понятие АС позволит при моделировании
семантически описывать классы, а их моделирование будет сводиться (рисунок. 1)
(обобщенная схема) к:
заданию и описанию основного
множества 
;
определению множества
операций 
;
заданию множества предикатов
для моделирования
поведение объектов и отношений между ними.
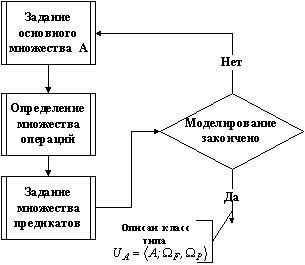
Рис. 1. Обобщенная схема последовательности семантического
описания классов.
Для представления класса
моделируемого пространства как абстракцию атрибутов и операций их обработки
будем применять систему 
, где 
- основное множество
алгебры и 
- совокупность частичных
операций, определенных на 
. Такая система будет иметь тип 
и сигнатуру 
. Необходимо заметить, что если каждая из операций,
принадлежащих сигнатуре 
, всюду определена на множестве 
, то алгебра 
будет универсальной.
Это является очень важным свойством абстрактных алгебр, так как по определению
класса согласно [11,12] все абстракции операций, соответствующие семейству 
, должны иметь свой функциональный смысл для множества
атрибутов, представленных множеством 
.
При моделировании классов
следует также иметь в виду, что класс, как вычислительная структура [5-8]
описывается в виде многоосновной алгебры (МА), которая представляет собой
систему 
. Последняя включает семейства основных множеств 
и сигнатуры операций 
, определенных на семействе 
следующим образом:
каждой 
местной операции 
однозначно сопоставлен
кортеж 
- схема данной операции,
так что 
является отображением
декартова произведения 
в множество 
где 
. Таким образом, в многоосновных алгебрах вместо основного
множества будем использовать семейство 
основных множеств, и
операции 
, которые являются 
местными функциями 
, аргументы которых 
определены на
множествах 
. Сама же функция 
принимает значения из
множества 
. Причем каждая нульарная операция 
фиксирует в множестве
некоторый элемент
(константу) 
. Необходимо отметить, что элементами многоосновной алгебры 
являются элементы ее
основных множеств 
. Если семейство 
состоит из одной
компоненты 
, то алгебра будет универсальной, то есть 
. В дальнейшем при моделировании классов будем учитывать, что
на многоосновные алгебры распространяются все определения и конструкции универсальных
алгебр.
На основании изложенного
сделаем вывод о том, что алгебра, состоящая из некоторого семейства множеств 
, где 
- основное множество
со свойствами, описанными выше, является конструкцией для семантического описания
классов. Очевидно, что аналогия состоит в том, что если система 
объединяет основные
множества с операциями 
, определенными на них, то класс это набор атрибутов,
принимающих собственные значения в одном из объектов, населяющих этот класс.
Все операции для объектов класса универсальны.
Таким образом, для
моделирования классов, состоящих из множества объектов, применим многоосновные
алгебры 
, а для моделирования объектов, как компонентов класса -
алгебраическую систему 
.
Одним из основных действий
при моделировании класса является задание имени класса 
(рисунок 1). Для
этого будем использовать стандартные обозначения или изображения [7,8]. Задание
имени происходит в произвольной форме, но чаще всего в символьном виде,
например строчной буквой или набором из букв (русского, английского) алфавита,
т.е. в виде, удобном для уяснения смысла понятия, абстрагированного в классе.
При этом имя класса, как правило, записывают с применением кавычек с обеих
сторон записи или скобок (фигурных, квадратных, угловых).
Описанный подход
устанавливает строгую математическую связь между данными и операциями, что
доказывает справедливость концептуальной основы объектного подхода –
совместного хранения свойств и функций моделируемого объекта реального мира. Такую
математическую формализацию целесообразно применять в тех случаях, если требуется
выполнить проверку получаемых данных на этапах информационного моделирования.
Предложенные математические выводы рекомендуется реализовать в виде алгоритмов
в системах автоматизированной разработки программного обеспечения.
ЛИТЕРАТУРА
1.
Мальцев А.И. Алгоритмы и рекурсивные функции. - М.: Наука. Гл. ред. физ.-мат.
лит., 1986. - 368 с.
2.
Мальцев А.И. Алгебраические системы. - М.: Наука. Гл. ред. физ.-мат. лит.,
1970. - 392 с.
3.
Бауэр Ф. Л., Гооз Г. Информатика. Вводный курс: в 2-х ч. Ч. 1: Пер. с нем. -
М.: Мир, 1990. - 336 с., ил.
4.
Бауэр Ф. Л., Гооз Г. Информатика. Вводный курс: в 2-х ч. Ч. 2 Пер. с нем. - М.:
Мир, 1990. - 423 с., ил.
5.
Агафонов В.Н. Типы и абстракции данных в языках программирования (обзор)//
Данные в языках программирования. м.: Мир, 1982. - с. 265-327.
6.
Агафонов В.Н. Объектно-ориентированное программирование и абстрактные типы
данных//Программирование. - 1990 № 6. - с.- 27-31
7.
Глотова Т.В. Информационное и программное обеспечение топологического проектирования
электронной аппаратуры на основе абстрактных типов данных. Диссертация ... канд.
техн. наук. Пенза. ППИ. 1992.
8.
Тыугу Э. Х. Объектно-ориентированное программирование. //Программирование. -
1990 № 6. - с. 16-26.
9.
Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л.
Алгебра языки программирование. К.,”Наукова думка”, 1978. - 312 с.
10.
М.Гросс, А.Лантен. Теория формальных грамматик. Пер. с фр.- М.: Мир. 1971. -
294 с.
11.
Буч Г. Объектно-ориентированное проектирование с примерами применения: Пер. с
англ. - М.: Конкорд, 1992. - 519 с.
12.
Шлеер С., Меллор С. Объектно-ориентированный анализ: Моделирование мира в состояниях./Пер.
с англ.- К.:Диалектика, 1993.-240 с.
Application of methods of abstract algebra
In working out of a supply with information
of systems
The automated working out of computer models
Mamanovich К.
In the given work the object-oriented approach applied now for information modeling of difficult program complexes is considered. The way of the mathematical description and the semantic data presentation, based on methods of abstract algebra is stated. For a mathematical basis the algebraic system is chosen. Its application is based on key concept of the objective approach - association in uniform information structure of set of data, as base properties of object and the operations which are carried out over them, as the functions describing behavior of object in the real world. Such approach allows mathematical to describe precisely information models, regarding concerning abstract types of data, that in turn will allow to execute verification of elements of the received information models.
Key
words: abstract
algebra, information models.
Кафедра вычислительной
техники
Военная академия войсковой
ПВО
Вооруженных Сил Российской Федерации
имени Маршала Советского Союза А.М. Василевского
(ВА ВПВО ВС РФ)
Поступила в редакцию 2.12.2009.