Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 8. -
Вып. 4. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm
УДК
621.396.969
Измерение
радиолокационными многоканальными измерителями координат отдельных целей из состава
групповых при использовании пространственно-временной корреляционной матрицы
сигнала
Ó 2009 г. Васильченко О. В.
Рассмотрен подход решения задачи определения числа источников
излучения, образовавших входной сигнал многоканального измерителя, основанный
на формировании и анализе пространственно-временной корреляционной матрицы
принимаемого сигнала. Суть предлагаемого подхода раскрыта на примере
многоканального измерителя построенного на базе активной фазированной антенной
решетки, в котором осуществляется согласованная пространственно-временная
обработка сигнала.
Ключевые слова: многоканальный измеритель координат, корреляционная матрица, активная
фазированная антенная решетка.
Известно, что задачей радиолокационного измерителя является определение
параметров (угловых координат, дальности, скорости и других) источников сигналов, поступающих на его
вход. В зависимости от типа радиолокационного измерителя его входной сигнал
может представлять собой переотраженный зондирующий, или излученный некоторыми
сторонними источниками.
В настоящей статье будет рассматриваться первая ситуация, характерная для
широко распространенных систем активной локации с пассивным ответом [1].
Для определенности будем считать, что многоканальный измеритель построен
на базе радиолокационной станции (РЛС) с активной фазированной антенной
решеткой (АФАР). АФАР представляет собой совокупность приемо-передающих модулей
(ППМ), каждый из которых соединен с
независимым антенным элементом решетки, определенным образом ориентированным в
пространстве. В режиме передачи все ППМ излучают зондирующий сигнал в
определенном направлении, причем
направление излучения определяется параметрами амплитудно-фазового распределения
по раскрыву антенны. В режиме приема напряжения на выходах приемных частей ППМ
одновременно при помощи аналого-цифровых преобразователей (АЦП) преобразуются в
цифровой код и обрабатываются совместно в универсальных или специализированных
ЭВМ. Преимуществами АФАР являются [2, 3]:
за счет преимуществ пространственной многоканальности и электронного
сканирования проводить быстрый обзор широкого сектора пространства;
за счет использования цифровой
техники обрабатывать сигнал параллельно несколькими методами с последующим
объединением результатов, что позволит получать высокие точности при измерении координат воздушных целей;
одновременно измерять параметры большого числа целей, находящихся в зоне
разведки;
обеспечивать разрешение воздушных целей, находящихся в одном импульсном
объеме;
эффективно адаптироваться к помеховой обстановке, создаваемой большим
количеством постановщиков помех;
измерять параметры прикрываемых помехопостановщиками целей, даже если помехопостановщик и цель находятся
в одном импульсном объеме;
значительно повысить уровень унификации РЛС различного назначения и
частотных диапазонов.
Среди всего многообразия
антенных решеток наиболее широкое применение имеют линейные и плоские
эквидистантные решетки. Объяснением этому является простота формирования
диаграмм направленности антенн (ДНА) в режимах передачи и приема. Сигнал,
сформированный М источниками
переизлучения и измеренный в пространственном канале линейной АФАР с номером r в
дискретный момент времени s будет иметь вид:
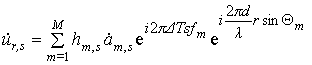, (1)
где 
– амплитуда сигнала m-го источника в s-й момент времени; fm - частота сигнала m-го источника;Θm – направление прихода
сигнала m-го источника; λ –
длина волны зондирующего сигнала; d –
расстояние между элементами; ΔT –
период дискретизации АЦП; hm,s – функция включения сигнала
m-го источника, равная единице в дискретные отсчеты времени
tзm≤sΔT< tзm +τИ ,
(2)
где tзm – время запаздывания
сигнала m-го источника, определяемое его дальностью; τИ
– длительность импульса.
Наиболее часто в качестве метода измерения угловых координат, частот и времен запаздывания сигналов используют функцию правдоподобия (ФП) вида
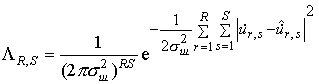, (3)
или ее различные модификации [1]. Причиной этого
является возможность получения близких к потенциальным точностных характеристик
при определенных распределениях помеховых и шумовых составляющих. Непременными
условиями возможности использования выражения (3) для решения задач измерения
координат целей являются известность модели (оценки) сигнала 
и достаточно высокая
степень соответствия ее истинным измеренным напряжениям вида (1).
Однако, даже при выполнении
этих условий, практическое использование ФП вида (2) связано со значительными
трудностями, обусловленными зачастую неприемлемыми объемами вычислительных
затрат при больших R и S, а также сложностью построения алгоритмов, обеспечивающих надежное
отыскание максимума ФП.
По этим причинам на практике
чаще всего используются квазиоптимальные методы и способы измерения координат и
параметров движения целей, причем, как правило, измерительные алгоритмы реализуются
раздельно в пространственной и временной областях.
При этом практически всегда
возникают сложности с разрешением групповых целей по угловым координатам и измерению
направлений прихода их сигналов. Объясняется это тем, что линейные расстояния
между отдельными целями из состава групповых в плоскости, перпендикулярной
линии визирования, как правило, много меньше ширины ДНА в этой плоскости. Этот
фактор затрудняет правильное определение числа отдельных целей в составе
групповой и измерение их угловых координат в ситуациях, когда они не
разрешаются по дальности или радиальной скорости.
Для преодоления этого
фактора в статье предлагается подход, основанный на формировании
пространственно-временной корреляционной матрицы принимаемого сигнала (КМС), и
извлечении из этой матрицы информации о числе и параметрах отдельных целей из
состава групповой.
Суть предлагаемого подхода рассмотрим на примере
многоканального измерителя построенного на базе АФАР, в котором осуществляется
согласованная пространственно-временная обработка сигнала, суть которой
заключается в следующем:
1. В каждом канале АФАР выполняется согласованная
внутрипериодная обработка сигнала, в результате которой формируются комплексные
отсчеты взаимокорреляционных функций принятого и зондирующего сигнала.
2. В каждом отсчете дальности каждого канала АФАР по
пачкам из S импульсов осуществляется когерентное накопление сигнала
(межпериодная обработка), в результате которой формируются сигналы S частотных фильтров.
3. По выходным сигналам одноименных частотных фильтров
всех R каналов АФАР выполняется согласованная пространственная
обработка (когерентное накопление, или формирование многолучевой ДНА).
С учетом сказанного, сигнал пространственного канала с
номером r, сформированный М
целями и измеренный в дискретный момент времени с номером s на выходе частотного фильтра с
номером k будет иметь вид:
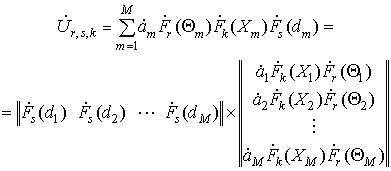, (4)
где 
– значение
характеристики направленности (ХН) антенны r-го канала в направлении
прихода сигнала m-го источника; 
– взаимокорреляционная функция (ВКФ) сигнала и его цифровой
копии, которая связывает дискретный отсчет дальности с номером s, в котором начинается цифровая
копия сигнала с дискретными отсчетами дальности dm, в которых начинаются сигналы
каждой отдельной цели из состава групповой.
Далее, в пространственном канале с наивысшим уровнем
сигнала, из напряжений вида (4), измеренных в одноименных отсчетах дальности и
в частотных фильтрах с максимальным уровнем сигнала любым известным из
литературы способом определяется число целей М, дальности до них dm, вычисляются значения 
. Одним из свойств и достоинств АФАР является высокая
идентичность значений 
и 
для всех пространственных
каналов, обусловленная формированием их в цифровом виде при помощи одинаковых
алгоритмов. Это позволяет использовать свойство их идентичности для определения
направлений прихода сигналов всех М
целей.
Для этого при помощи М
напряжений в отсчетах дальности с номерами n1…nM пространственного канала с
номером rmax и
вычисленных значений 
составляются системы
уравнений вида:
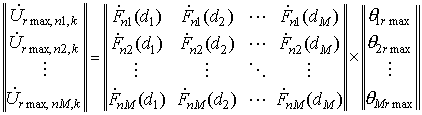(5)
Сравнение системы уравнений (5) с уравнением (4)
показывает, что элементы формально введенного вектор-столбца неизвестных
║θ║ представляют собой не что иное, как произведения
амплитуд сигналов целей на значения частотных характеристик фильтра k и характеристик направленности
пространственного канала rmax:
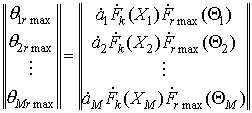(6)
Далее, основываясь на свойстве одинаковости 
и 
для всех пространственных
каналов, системы уравнений вида (5) составляются в любом другом пространственном
канале с номером r (предпочтительнее всего, в соседнем с rmax).
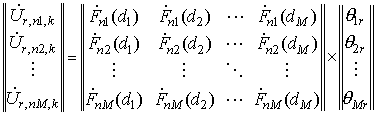(7)
Решения этой системы уравнений представляют собой
величины вида
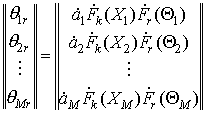(8)
Отношение одноименных элементов вектор-солбцов (8) и (6)
позволяет получить пеленговые направления на цели (по аналогии с моноимпульсными системами с заданной формой
пеленгационной характеристики) в виде отношений значений характеристик направленности
двух пространственных каналов в направлении на m-й источник излучения.
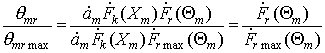(9)
Очевидно, что при использовании двумерной антенной
решетки, перечисленные выше действия позволят определять две угловые координаты
каждой цели перпендикулярных плоскостях.
Аналогично можно показать, что в ситуациях, когда
сигналы различных целей отличаются частотами (скоростями полета), то
определение числа целей и их частот целесообразно выполнять по корреляционной
матрице сигнала, составленной описанными выше способами в частотной области,
после чего, основываясь на перечисленных выше свойствах обработки сигналов в
АФАР, вычислять дальности каждой цели и ее угловые координаты.
Таким образом, предложенный подход предполагает
формирование КМС во временной области, определение числа целей, имеющих
различную дальность или скорость, определение дальности (скорости) каждой цели
и последующее вычисление амплитуд и направлений прихода сигналов целей при
помощи напряжений соседних пространственных каналов.
Следует заметить, использование предлагаемого подхода
возможно в ситуациях, когда сигналы целей не разрешаются ни по одной из
измеряемых координат.
ЛИТЕРАТУРА
1. Ширман Я. Д., Манжос В. Н. Теория и техника обработки радиолокационной
информации на фоне помех. М.: Радио и связь, 1981. 416 с.
2. Воскресенский Д. И. Канащенков
А. И. Активные фазированные
антенные решетки. М.: Радиотехника ,2004. 488 с.
3. Варюхин В. А. Основы теории многоканального анализа. - Киев:
ВА ПВО СВ, - 1993.
- 171 с.
Radar multichannel indicators
dimension of coordinates of separate objects in composition of groups in use of
space-time correlation signal matrix
Vasilchenko
O. V
The
approach to the decision of the definition task of the numbers of emitting
sources is examined; the emitting sources formed an input signal of
multichannel indicator, based on the formation and analysis of space-time correlation
matrix of the accepted signal. The suggested access essence is expanded on the
example of multichannel indicator based on active phased antenna array, in
which matched space-time signal processing is carrying out.
Key words: multichannel indicator, correlation
matrix, active phased antenna array.
Научно-исследовательский
отдел
Военная академия войсковой
ПВО
Вооруженных Сил Российской
Федерации
имени Маршала Советского Союза А.М. Василевского
(ВА ВПВО ВС РФ)
Поступила в редакцию 2.12.2009.