Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 8. -

Вып. 4. - 2009. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm

 

УДК 621.396.96

 

АНАЛИТИЧЕСКОЕ ОПИСАНИЕ КОРРЕЛЯЦИОННОГО МНОГОЧАСТОТНОГО СПОСОБА ОЦЕНКИ РАДИАЛЬНЫХ РАЗМЕРОВ ВОЗДУШНЫХ ЦЕЛЕЙ

 

Ó 2009 г. Юдин В. А.

 

(yudin-2.doc)

 

Получена математическая модель отклика устройства обработки, вычисляющего среднее значение модуля разности сигналов, разнесенных по частоте, при отражении от групповой сосредоточенной цели, что необходимо для оценки радиальных размеров воздушных объектов.

Ключевые слова: многочастотный способ распознавания

 

Одним из сигнальных признаков распознавания воздушных целей (ВЦ) является параметр e, характеризующий частотную корреляцию флюктуаций эффективной поверхности рассеяния (ЭПР) цели при дискретной перестройке частоты сигнала РЛС, определяемый выражением [1, 2]

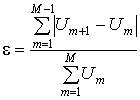,                                                         (1)

где Um и Um+1 – амплитуды отраженных от цели составляющих многочастотного сигнала (МЧС) соответственно на m-й и (m+1)-й частотах; М – число частот в многочастотном сигнале РЛС.

Применение МЧС в этом признаке распознавания необходимо для получения среднего значения модуля разности отраженных от цели сигналов, разнесенных по частоте на величину DF, и его нормировки. Исходя из этого, выражение (1) можно переписать в виде:

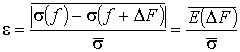                   ,                                            (2)

где s – мгновенная ЭПР цели; f – несущая частота зондирующего сигнала (ЗС);  – средняя ЭПР цели.

Обозначение

                                               (3)

принято для того, чтобы подчеркнуть зависимость признака распознавания e от разноса частоты многочастотного ЗС.

Сложный характер зависимости параметра e от числа, положения и интенсивности блестящих точек (БТ) объекта затрудняет изучение закономерностей его изменения при изменении разноса частот МЧС DF и радиального размера целей. Для моделей сложных радиолокационных целей (РЛЦ) с произвольным числом БТ это возможно только статистическими методами.

Для уяснения общих закономерностей изменения параметра e при рассеянии объектами сложной формы МЧС проследим главные из них на простейшей модели цели, состоящей из двух БТ с s1=s2=s (гантельная модель цели). Для этого получим аналитическое выражение  для гантельной модели цели, для которой

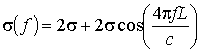,                                                (4)

где L – радиальный размер цели; с – скорость распространения электромагнитных волн.

Подставляя (4) в (3), можно записать:

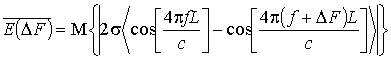.                            (5)

После преобразования разности тригонометрических функций и приняв , (где f0 – центральная несущая частота ЗС), выражение (5) перепишется в виде:

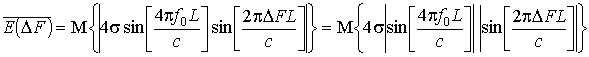. (6)

Вынося за знак математического ожидания (МОЖ) медленно изменяющийся член выражения (6) (принят постоянным), запишем:

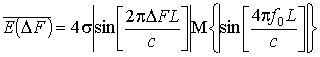.                                 (7)

Для равномерно распределенного аргумента фазового множителя 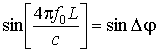 на интервале [0, 2p) можно найти:

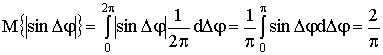.                        (8)

Подставляя (8) в (7), для гантельной модели цели окончательно получим:

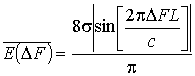.                                                (9)

Подставляя (9) в (2), при средней ЭПР для гантельной модели цели  можно получить выражение для параметра e:

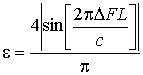.                                                    (10)

Анализ выражений (9) и (10) показывает, что при увеличении разноса частот характер изменения параметра e определяется для гантельной модели цели только ее радиальным размером (пространственным смещением по дальности БТ относительно друг друга).

Для цели, состоящей из множества БТ, аналогично как для гантельной модели цели можно получить:

 

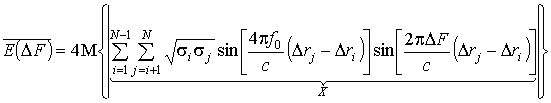,      (11)

где Dri(j) –  смещение i(j)-й блестящей точки вдоль линии визирования РЛС относительно первой БТ; N – число БТ на «освещенной» поверхности цели.

Нахождение МОЖ модуля суммы большого числа слагаемых является непростой аналитической задачей. Возможным путем ее решения является следующий.

Обозначим в (11) выражение, стоящее под знаком модуля, за Х, тогда (11) сведется к виду:

,                                                      (12)

где Х – случайная величина, в силу центральной предельной теоремы [3] распределенная по нормальному закону с МОЖ М{Х}=0 и дисперсией D{Х}=D, плотность распределения которой

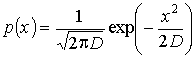.                                               (13)

Согласно теореме о МОЖ функции случайного аргумента [3] можно записать

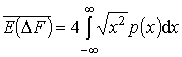.                                                 (14)

Подставляя (13) в (14), найдем:

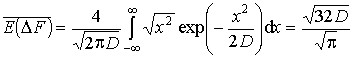.                           (15)

Используя теоремы о дисперсии функции случайных величин [3], можно найти:

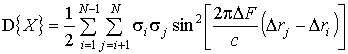.                            (16)

Подставляя (16) в (15), для цели, состоящей из множества БТ, получим:

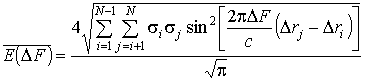.                        (17)

Для гантельной модели цели выражение (17) преобразуется к виду

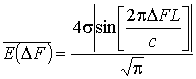.                                               (18)

Вычисление значения  для гантельной модели цели по выражению (18) дает относительную ошибку 11% по сравнению с вычислением по выражению (9). Эта незначительная ошибка объясняется тем, что в (11) обозначенное за Х выражение для гантельной модели цели сводится к одному слагаемому вида

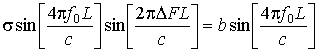
(где b = const), имеющему распределение, отличное от нормального:

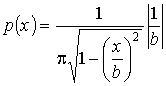.                                                   (19)

Подставляя (19) в (14), заменяя пределы интегрирования на от –b до b, можно найти:

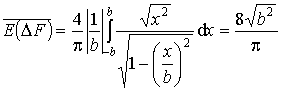.                                   (20)

Подставляя в (20) 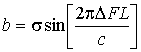, получим точное выражение для гантельной модели цели (9), что подтверждает правомерность предложенной методики нахождения величины  для цели, состоящей из множества БТ.

При увеличении количества БТ N, т. е. при увеличении числа слагаемых в выражении (11), принятом за Х,  будет постепенно стремиться к виду (17).

Таким образом, учитывая, что 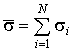 и подставляя (17) в (2), можно окончательно получить математическую модель признака распознавания классов ВЦ корреляционным многочастотным способом, приведенную к единой модели сложной радиолокационной цели

.

 

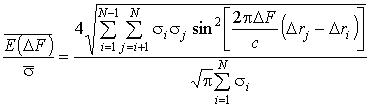ЛИТЕРАТУРА

 

1.     Трубицин Е. Г., Ермоленко В. П. Алгоритмы распознавания сложных воздушных целей//Зарубежная радиоэлектроника, 1992. № 10. - С. 82–84.

2.     Ермоленко В. П., Митрофанов Д. Г., Коваленков Н. Н. Учет вида зондирующего сигнала и архитектурных особенностей радиолокационных целей при определении потенциальных возможностей их распознавания//Зарубежная радиоэлектроника, 1996. № 11. - С. 73–76.

3.     Вентцель Е. С. Теория вероятностей. М., Высш. шк., 2001. - 576 с.

 

THE ANALYTICAL DESCRIPTION OF THE CORRELATION MULTIFREQUENCY WAY OF THE ESTIMATION OF THE RADIAL SIZES OF THE AIR PURPOSES

 

Yudin V. A.

 

The mathematical model of the response of the device of the processing calculating average value of the module of a difference of signals, carried on frequency is received, at reflection from the group concentrated purpose that is necessary for an estimation of the radial sizes of air objects.

Кеу words: a multifrequency way of recognition

 

Проведенные исследования поддержаны РФФИ (грант № 09-07-97519).

Кафедра радиотехники

Академия войсковой ПВО Вооруженных Сил РФ

им. Маршала Советского Союза А. М. Василевского, г. Смоленск

Поступила в редакцию 18.11.2009.