Математическая морфология.

Электронный математический и медико-биологический журнал. - Т. 8. -

Вып. 4. - 2009. - URL:

http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM

http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm

http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm

 

УДК 621.396.96

 

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАДИОЛОКАЦИОННОГО КАНАЛА  ИМИТАЦИОННОЙ МОДЕЛИ СИСТЕМЫ РАСПОЗНАВАНИЯ КЛАССОВ ВОЗДУШНЫХ ЦЕЛЕЙ ДЛЯ РЛС ОБНАРУЖЕНИЯ

 

Ó 2009 г. Панов Д. В., Юдин В. А., Чижов А. А., Васильченко О. В.

 

(yudin-3.doc)

 

Разработана цифровая имитационная математическая модель системы распознавания классов ВЦ РЛС обнаружения, учитывающая режим работ РЛС, ее реальные технические характеристики, статистику флюктуационных помех, динамику полета цели (в том числе траекторные нестабильности). Модель позволяет исследовать вероятностные характеристики системы распознавания классов воздушных целей при использовании двух- и многочастотных методов оценки радиальных размеров воздушных объектов в РЛС обнаружения различного диапазона длин волн.

Ключевые слова: цифровая имитационная модель

 

Задачей разработки цифровой имитационной математической модели системы распознавания классов воздушных целей (ВЦ) является исследование с ее использованием различительных свойств двух- и многочастотных методов оценки радиальных размеров ВЦ в РЛС различного диапазона длин волн.

Обобщенная структурная схема цифровой имитационной математической модели приведена на рис. 1 [1, 2].

 

 

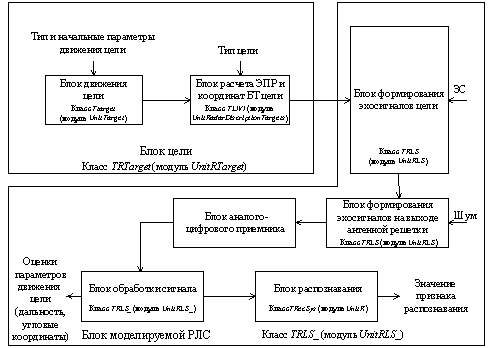
Рис. 1. Обобщенная структурная схема цифровой имитационной математической модели системы распознавания классов ВЦ

 

Функционирование имитационной модели начинается с выбора реализуемого метода распознавания, количества используемых M обзоров, S частот МЧС и Nстат циклов для набора статистики. Исходные данные для процесса моделирования задаются с помощью окна InitialWindow, описанного в модуле RS_Initial (класс TInitialForm). В этом же модуле хранятся используемые по умолчанию значения всех параметров моделирования.

Управление процессом вычислений (запуск и приостановка) осуществляется через органы управления, расположенные в окне мониторинга (класс TMonitorForm, описанный в модуле Monitor), кроме того, в данном окне отображаются текущие результаты моделирования (рис. 2).

 

 

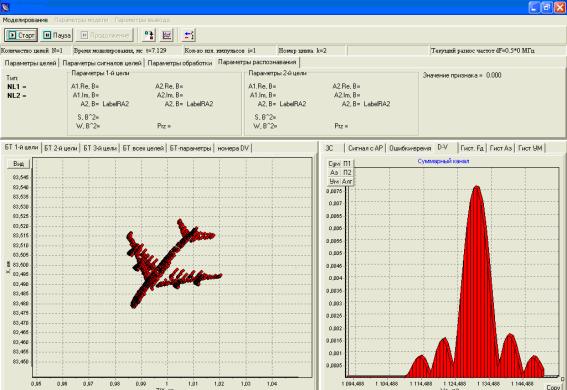
Рис. 2. Вид окна управления процессом вычислений

 

Процесс вычислений программно реализован в виде отдельного потока вычислений (класс TProcess=class(TThread), описанный в модуле UnitProcess) и осуществляется в следующем порядке [3]. Из заданных диапазонов координат, скоростей, углов тангажа и рыскания случайным образом формируются характеристики траекторий цели (рис. 3). Координаты и параметры движения цели в зависимости от типа маневра и начальных установок рассчитываются на каждом интервале временной дискретизации модели в блоке движения цели (метод TTarget.Outy класса TTarget, описанного в модуле UnitTarget).

В отсутствии маневра цель движется прямолинейно и равномерно в заданном направлении. Маневр № 1 подразумевает незначительные случайные траекторные нестабильности (нормальные ускорения в плоскостях вертикального и бокового движения задаются винеровскими процессами). Маневры №№ 2, 3, 4, 5 отличаются характером дополнительных регулярных составляющих нормальных ускорений.

 

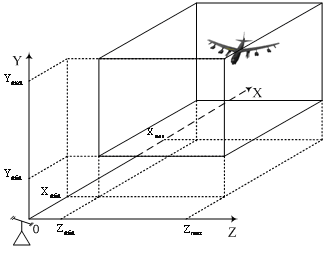
Рис. 3. Иллюстрация выбора координат цели из заданных диапазонов

 

По рассчитанным углам визирования цели может быть установлен максимум диаграммы направленности антенны (ДНА) или имитироваться процедура сканирования ДНА. ДНА задается таблицами, расчет значений которых производится по специальной методике.

Класс TLIVI, соответствующий совокупности блестящих точек (БТ) цели, имеет метод Outy, в котором в зависимости от типа цели и ракурса ее облучения рассчитываются эффективные поверхности рассеяния (ЭПР) (массив A) и координаты БТ в связанной системе координат цели (массивы X1, Y1, Z1 для координат по осям x, y и z соответственно) (рис. 4).

На каждом интервале временной дискретизации модели координаты цели () рассчитываются относительно начала земной системы координат.

Для расчета ЭПР БТ используются определяющие ракурсы облучения цели, курсовой угол на РЛС  и угол места цели , а также углы  и . Значения углов  и определяются, исходя из координат цели в параметрической системе координат Sп, Hп и Pп:

 

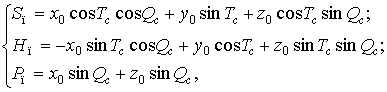                   (1)

 

где  и  – курс и угол наклона траектории цели.

 

 

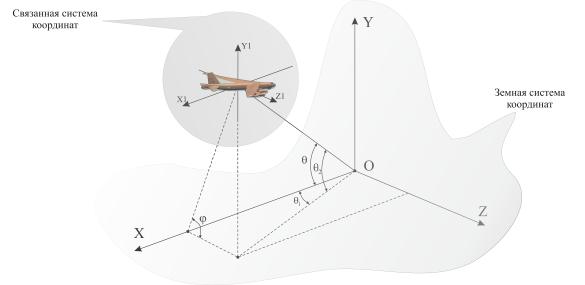
Рис. 4. Иллюстрация вычисления координат цели в связанной и земной

системах координат

 

Связь между углами ,  и ,  определяется выражениями

 

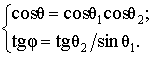                                             (2)

При изменении ракурса облучения цели больше установленного значения

 

,                                                (3)

 

где  – минимальное значение изменения углов  и , учитываемое при расчете ЭПР БТ, производится вызов процедуры LIVI.Outy и осуществляется пересчет ЭПР (массив A) и координат БТ цели (массивы X1, Y1, Z1).

Методом TRTarget.LIVIOutZemlya осуществляется пересчет координат всех БТ в земную систему координат (массивы X, Y, Z) (рис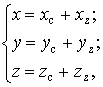. 4)

 

                                                      (4)

где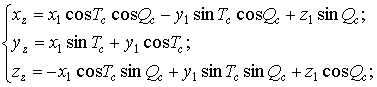

 – координаты начала отсчета связанной системы координат относительно земной системы координат;

 – координаты БТ в связанной системе координат.

Блоку формирования эхосигналов цели (рис. 1) соответствует метод TRLS.XSignalForm класса TRLS, описанного в модуле UnitRLS. В методе TRLS.XSignalForm для каждой БТ цели, ЭПР которой превышает задаваемое в установках минимальное значение , определяются:

дальность Д и время tз прохождения электромагнитной волны (ЭМВ) до БТ

 

напряжение зондирующего сигнала (ЗС), облучавшего БТ (текущее значение ЗС, облучавшего цель хранится в одномерном массиве ZS, соответствующем используемому зондирующему сигналу),

коэффициент усиления антенны по напряжению и ослабление ЭМВ;

значение набега фазы;

пеленг БТ;

комплексный множитель ДНА на передачу;

комплексный множитель ДНА на прием.

С учетом вышеуказанных факторов вычисляется мгновенное значение комплексной огибающей (КО) эхосигнала БТ для момента времени ti его приема

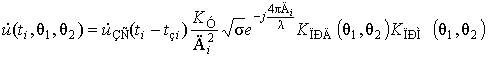,       (5)

 

где

–

коэффициент усиления антенны по напряжению;

 

–

длина волны зондирующего сигнала;

 

–

ЭПР БТ;

 

 

–

–

комплексный множитель ДНА на передачу;

комплексный множитель ДНА на прием.

 

 

 

 

 

 

 

Значения КО эхосигнала для каждой БТ записываются с помощью метода AddSpace аддитивно в буфер Space в ячейку, соответствующую моменту приема данных значений КО (в ячейку, чтение из которой будет выполняться в момент времени, соответствующий моменту приема данного значения КО). Буфер Space является кольцевым. Количество столбцов буфера равно максимальному времени запаздывания эхосигнала. Указатель буфера (поле TRLS.NSp), определяющий некоторый номер столбца, ассоциирован с текущим моментом времени. Соответственно для каждой БТ запись значений КО ее эхосигналов производится в ячейку (столбец), отстоящую от текущей (от значения указателя) на время запаздывания эхосигнала этой БТ.

Кольцевая структура буфера объясняется следующим. В случае, если номер ячейки N, в которую производится запись, превышает размер буфера (поле NSpaceMax), то запись производится в ячейку с номером N–NSpaceMax, что позволяет реализовать неограниченное время моделирования (поскольку значение указателя буфера NSp – текущего момента времени – также сбрасывается (становится равным единице) при превышении им значения NSpaceMax). Таким образом, буфер Space имитирует физические процессы запаздывания и интерференции эхосигналов БТ в среде распространения ЭМВ.

Блок формирования сигналов на выходе антенной решетки реализован с помощью метода TRLS.YSignalFormAndProcessing. Метод выполняет чтение значений КО эхосигнала из ячейки буфера Space (метод GetSpace), номер которой (NSp) соответствует текущему моменту времени, и записывает значения в массив AR. Для уменьшения вычислительных затрат оцифровывается не весь временной интервал возможного прихода эхосигнала, а только его часть в окрестности эхосигнала цели, соответствующая τи±10 мкс. Таким образом, количество ячеек массива AR соответствует вышеуказанному временному интервалу. Значения КО эхосигнала записываются в ячейку массива AR, номер которой соответствует времени, прошедшему от начала цикла обработки. Ячейки буфера Space, из которых произведено чтение, обнуляются для обеспечения возможности повторного (многократного) их использования методом AddSpace. К принятому антенной решеткой сигналу (сигналу, считанному из буфера Space) прибавляется дискретное значение белого гауссовского шума с нулевым математическим ожиданием и заданной дисперсией.

Таким образом, к концу цикла обработки массив AR представляет собой массив комплексных огибающих сигналов на выходе антенной решетки, принятых на фоне шумовых помех в данном цикле. В конце цикла вызывается метод TRLS.Processing, соответствующий блокам аналого-цифрового приемника и стандартной обработки (рис. 1).

В модели принято, что аналого-цифровой приемник идеальным образом оцифровывает комплексные огибающие сигналов в приемном канале с заданной частотой дискретизации. Оцифрованные комплексные огибающие эхосигналов суммируются в пределах стробов (дискретность расстановки которых может варьироваться), результаты суммирования поступают в блок обработки сигнала (рис. 1). В блоке обработки осуществляется корреляционная обработка эхосигнала, пороговая обработка, выделение максимума отклика и оценивание параметров радиолокационной цели.

Математическая модель комплексной огибающей копии используемого в РЛС ЛЧМ зондирующего сигнала имеет вид:                   

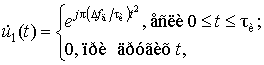                                     (6)

где  – девиация частоты.

Математическую модель комплексной огибающей отраженного от точечной цели ЛЧМ сигнала можно представить как

.                                    (7)

Аналитическая запись корреляционного интеграла для дискретных значений сдвигов опорных сигналов имеет вид:

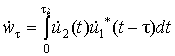.                                       (8)

На рис. 5 приведены результаты корреляционной обработки (формы откликов приемника), полученные по имитационной модели (а) и по выражению (8) (б) для РЛС обнаружения.

Совпадение вышеуказанных форм откликов приемников свидетельствует об адекватности модели радиолокационного канала разработанной имитационной модели системы распознавания классов ВЦ реальным условиям.

 

 

 

 

 

 

 

 

 


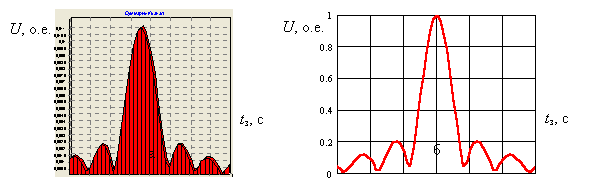
Рис. 5. Результаты корреляционной обработки, полученные по имитационной модели (а) и по выражению (8) (б)

 

Результаты обработки заносятся в массив OutMatr. В блоке распознавания на основе измеренных комплексных амплитуд отраженных сигналов (рис. 1) могут быть реализованы различные алгоритмы распознавания, что позволяет сформировать текущие оценки сигнальных признаков распознавания.

Процесс вычислений завершается выполнением метода System.Outy (описанного в модуле UnitSystem), где рассчитывается системное время моделирования и осуществляется организация набора статистических данных.

Таким образом, разработанная цифровая имитационная математическая модель системы распознавания классов ВЦ РЛС обнаружения учитывает режим работ РЛС, ее реальные технические характеристики, статистику флюктуационных помех, динамику полета цели (в том числе траекторные нестабильности).

 

 

ЛИТЕРАТУРА

 

1. Чижов А. А., Панов Д. В., Юдин В. А., Васильченко О. В., Мурашкин А. В. Цифровая имитационная модель системы распознавания классов воздушных целей РЛС обнаружения метрового диапазона длин волн. Федеральное агентство по образованию. ФГНУ «Государственный координационный центр информационных технологий». Отраслевой фонд алгоритмов и программ. Свидетельство об отраслевой регистрации разработки № 12332, 2009.

2. Чижов А. А., Панов Д. В., Юдин В. А., Васильченко О. В., Караваев С. А. Цифровая имитационная модель системы распознавания классов воздушных целей РЛС обнаружения дециметрового диапазона длин волн. Федеральное агентство по образованию. ФГНУ «Государственный координационный центр информационных технологий». Отраслевой фонд алгоритмов и программ. Свидетельство об отраслевой регистрации разработки № 12333, 2009.

3. Чижов А. А., Панов Д. В., Краснов П. В. Цифровая имитационная модель распознавания классов радиолокационных целей многоканальной станцией наведения ракет типа 9С32. Депонированная рукопись. № А 28804. Сер. А. Вып. 3 (92). М.: ЦВНИ МО РФ, 2006. – 15 с.

 

 

MATHEMATICAL MODEL OF THE RADAR CHANNEL OF IMITATING MODEL OF SYSTEM OF RECOGNITION OF CLASSES OF THE AIR PURPOSES FOR RADAR DETECTION

 

Panov D. V., Yudin V. A., Chizhov A. A., Vasilchenko O. V.

 

The digital imitating mathematical model of system of recognition of classes the air purposes radar of the detection, considering a mode of works radar, its real characteristics, statistics handicapes, dynamics of flight of the purpose (including trajectory instability) is developed. The model allows to investigate likelihood characteristics of system of recognition of classes of the air purposes at use two -and multifrequency methods of an estimation of the radial sizes of air objects in radar detection of a various range of lengths of waves.

Key words: digital imitating model

 

Проведенные научные работы поддержаны президентом РФ (грант № МК-6.2008.10) и РФФИ (гранты № 09-07-97519, 08-07-97503).

 

Академия войсковой ПВО Вооруженных Сил РФ

им. Маршала Советского Союза А. М. Василевского, г. Смоленск

Поступила в редакцию 18.11.2009.