Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 8. -
Вып. 4. - 2009. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/TITL-24.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-24-html/cont.htm
УДК
621.391.161
Алгоритм
двумерной пространственной фильтрации разработанный на основе корреляционного
способа компенсации фона
Ó 2009 г. Жендарев М. В.
На основе корреляционного способа обнаружения тепловых объектов
разработан алгоритм двумерного пространственного фильтра, который может быть
реализован программно в видеопроцессоре теплопеленгатора. Алгоритм позволяет
автоматизировать процесс обнаружения воздушных целей (самолетов, вертолетов,
крылатых ракет, беспилотных летательных аппаратов и т. д.) и обеспечить вывод
их видеоизображений на монитор видеоконтрольного устройства в бинарном виде.
Ключевые слова: корреляционный способ, алгоритм двумерной пространственной
фильтрации, диагональная корреляционная матрица, массив изображения.
Основой алгоритма пространственной фильтрации, построенного
на основе способа корреляционной компенсации фона, является расчет диагональной
корреляционной матрицы 
по строкам и матрицы 
по столбцам для
массива 
ФЦИ [1]. Первая (центральная) диагональ каждой
корреляционной матрицы содержит элементы, равные единице, поскольку они
получены путем вычисления коэффициентов корреляции строки (столбца) с самим
собой. Вторая диагональ матрицы показывает, каков коэффициент взаимной корреляции
первой строки со второй, второй с третьей и т. д. Из элементов вторых диагоналей
корреляционных диагональных матриц 
и 
получают векторы 
и 
. Вектора 
, 
используются для
формирования массивов 
, в каждый элемент, (имеющий индексы n и m) которого
записывался результат умножения в соответствии с формулой 
, где 
и 
-
величины n-го и m-го элементов векторов 
и 
соответственно. По
адаптивному порогу 
, в соответствии с решающим правилом в элемент 
записывается 1, если
в соответствующем элементе массива 
. В элемент 
записывается 0, если
в соответствующем элементе массива 
. Таким образом, окончательно формируется массив 
. Массив 
используется для создания
бинарного изображения на мониторе ВКУ. По номерам строк и столбцов элементов, в
которых находятся единичные значения, определяется пространственное положение
цели в сегменте полусферы поиска. Изображение на мониторе теплокадра до и после
пространственной фильтрации представлено на рис. 1.
Для решения задачи предлагается использовать пространственную фильтрацию принятых сигналов. Блок-схема теплопеленгатора, реализующая предлагаемую пространственную фильтрацию, представлена на рис 2.
Пространственный фильтр предлагается реализовать программно в видеопроцессоре в соответствии с предлагаемым алгоритмом пространственной фильтрации [1,2].
|
|
|
|
|
а) |
|
б) |
Рис. 1. Изображение теплокадра на мониторе ВКУ, полученное до (а) после фильтрации (б)
Рассмотрим алгоритм пространственной фильтрации, построенный на основе метода корреляционной компенсации фона:
1. Получение массива
изображения 
из
аналогово-цифрового преобразователя видеопроцессора размером 
, где N - число строк, а M - число столбцов массива.
2. Расчет диагональной
корреляционной матрицы 
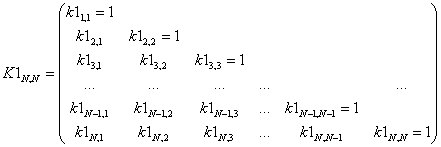, (1)
по строкам массива 
, элементы которой рассчитываются по формуле:
,
(2)
где 
- нормированный
коэффициент взаимной корреляции между n-ой и (n+k)-ой строками массива
изображения; 
, 
- напряжение, снимаемое с выхода элементарного
приемника, пропорциональное энергетической яркости излучения, расположенного в
n-ой и (n+k)-ой строках; 
, 
- математическое
ожидание напряжения в n-ой и (n+k)-ой строках; 
, 
- среднеквадратические
отклонения энергетических яркостей в n-ой и (n+k)-ой строках; M - количество элементов в столбце; k - шаг расчета нормированных коэффициентов
корреляции 
[3].
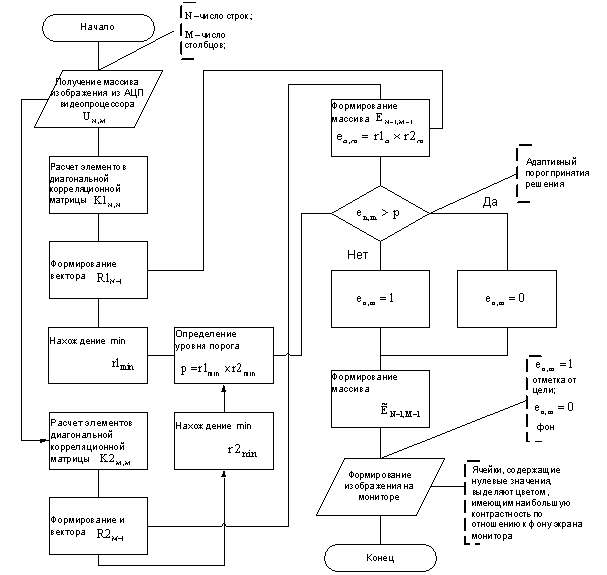
Рис. 2. Блок схема алгоритма
двумерной пространственной фильтрации,
построенного на основе способа
корреляционной компенсации фона
3. Формирование вектора
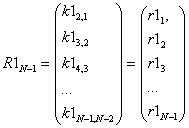(3)
из элементов второй
диагонали корреляционной диагональной
матрицы 
.
4. Расчет диагональной
корреляционной матрицы 
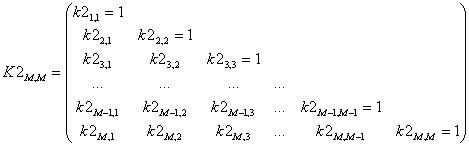, (4)
по столбцам массива 
, элементы которой рассчитываются по формуле:
,
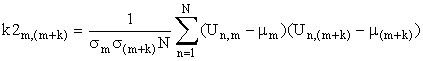(5)
где 
- нормированный коэффициент
взаимной корреляции между m-м и (m+k)-м
столбцами массива изображения; 
, 
- напряжение, снимаемое с выхода элементарного
приемника, пропорциональное энергетической яркости излучения, расположенного в
m-м и (m+k)-м столбце; 
, 
- математическое
ожидание напряжения в m-м и (m+k)-м столбце; 
, 
- среднеквадратические
отклонения энергетических яркостей в m-м и (m+k)-м столбце (строке); N - количество элементов в строке; k - шаг расчета нормированных коэффициентов
корреляции 
[3].
5. Формирование вектора
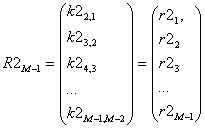, (6)
из элементов второй
диагонали корреляционной диагональной матрицы 
.
6. Формирование массива 
, в каждый элемент, имеющий индексы n и m, которого
записывают результат умножения в соответствии с формулой
, (7)
где 
и 
- величины n-го и m-го элементов векторов 
и 
соответственно.
7. Определение порога принятия
решения состоит из двух этапов. Первый этап имеет цель поиска минимальных
элементов 
и 
векторов 
и 
соответственно.
Второй этап заканчивается нахождением адаптивного порога принятия решения
рассчитывается по формуле:
. (8)
8. Пороговая обработка, в процессе которой сравнение величин элементов
массива 
с адаптивным
пороговым значением, равным p. Формирование массива принятия решения 
в соответствии с правилом:
при превышении величиной
элемента массива 
порогового значения,
величину элемента обнуляют;
если значение элемента
массива 
меньше или равно
пороговому значению, ему присваивают единичное значение.
9. Формирование фоноцелевого
изображения на мониторе видеоприемного устройства с использованием массива 
. Прямоугольный экран монитора видеоконтрольного устройства
делят на прямоугольные ячейки по числу строк и столбцов массива 
. Ячейки 
, содержащие единичные значения, выделяют цветом, имеющим
наибольшую контрастность по отношению к фону экрана монитора.
Для проверки
работоспособности предложенного способа двумерной пространственной фильтрации
было проведено предварительное математическое моделирование с использованием
математического пакета MathCAD [4-6]. Примерный вид теплокадра,
получаемого на мониторе ВКУ теплопеленгатора при наличии ВЦ по которому
предлагается проводить обнаружение цели, представлен на рис. 1, а. Изображение
получено в соответствии с массивом изображения 
, каждый элемент 
которого содержит
информацию о напряжении, пропорциональном яркости излучения фона, снятого с
ячейки многоэлементного приемника в n-й строке на m-м шаге. Массив 
с изображением ВЦ и
массив без него использовались для проведения математического моделирования.
Для массивов 
были рассчитаны
диагональные корреляционные матрицы 
по строкам и матрицы 
по столбцам. По ним
были получены вектора 
и 
из элементов вторых
диагоналей корреляционных диагональных матриц 
и 
. Примерные виды массивов 
, 
и векторов 
, 
, полученные для случаев наличия и отсутствия изображения ВЦ,
представлены в таблицах 1–10 [3].
Таблица 1 - Корреляционная матрица 
, рассчитанная для массива 
по строкам при отсутствии
ВЦ
|
№ стр. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
N-1 |
N |
|
1 |
1 |
|
|
|
|
|
|
|
… |
|
|
|
2 |
0,8256 |
1 |
|
|
|
|
|
|
… |
|
|
|
3 |
0,7912 |
0,8603 |
1 |
|
|
|
|
|
… |
|
|
|
4 |
0,7901 |
0,7837 |
0,8456 |
1 |
|
|
|
|
… |
|
|
|
5 |
0,7699 |
0,7498 |
0,7897 |
0,8534 |
1 |
|
|
|
… |
|
|
|
6 |
0,7905 |
0,7633 |
0,7822 |
0,8155 |
0,8563 |
1 |
|
|
… |
|
|
|
7 |
0,7931 |
0,7453 |
0,7887 |
0,7889 |
0,8028 |
0,8502 |
1 |
|
… |
|
|
|
8 |
0,7954 |
0,7738 |
0,7969 |
0,7929 |
0,7781 |
0,8082 |
0,8441 |
1 |
… |
|
|
|
9 |
0,7874 |
0,7699 |
0,7851 |
0,7855 |
0,7738 |
0,7869 |
0,7936 |
0,8618 |
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
N-1 |
0,8175 |
0,7616 |
0,7964 |
0,7883 |
0,7849 |
0,7953 |
0,7817 |
0,7950 |
… |
1 |
|
|
N |
0,7772 |
0,7791 |
0,7791 |
0,7664 |
0,7649 |
0,7670 |
0,7509 |
0,7675 |
… |
0,8588 |
1 |
Таблица 2 - Корреляционная матрица 
, рассчитанная для массива 
по строкам при наличии
ВЦ
|
№ стр. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
N-1 |
N |
|
1 |
1 |
|
|
|
|
|
|
|
… |
|
|
|
2 |
0,8256 |
1 |
|
|
|
|
|
|
… |
|
|
|
3 |
0,7912 |
0,8603 |
1 |
|
|
|
|
|
… |
|
|
|
4 |
0,7901 |
0,7837 |
0,8456 |
1 |
|
|
|
|
… |
|
|
|
5 |
0,4409 |
0,4500 |
0,4674 |
0,5162 |
1 |
|
|
|
… |
|
|
|
6 |
0,7905 |
0,7633 |
0,7822 |
0,8155 |
0,5251 |
1 |
|
|
… |
|
|
|
7 |
0,7931 |
0,7453 |
0,7887 |
0,7889 |
0,4733 |
0,8502 |
1 |
|
… |
|
|
|
8 |
0,7954 |
0,7738 |
0,7969 |
0,7929 |
0,4611 |
0,8082 |
0,8441 |
1 |
… |
|
|
|
9 |
0,7874 |
0,7699 |
0,7851 |
0,7855 |
0,4833 |
0,7869 |
0,7936 |
0,8618 |
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
N-1 |
0,8175 |
0,7616 |
0,7964 |
0,7883 |
0,4504 |
0,7953 |
0,7817 |
0,7950 |
… |
1 |
|
|
N |
0,7772 |
0,7791 |
0,7791 |
0,7664 |
0,4537 |
0,7670 |
0,7509 |
0,7675 |
… |
0,8588 |
1 |
Таблица 3 - Корреляционная матрица 
, рассчитанная для массива 
по столбцам при
отсутствии ВЦ
|
№ ст. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
M-1 |
M |
|
1 |
1 |
|
|
|
|
|
|
|
… |
|
|
|
2 |
0,9982 |
1 |
|
|
|
|
|
|
… |
|
|
|
3 |
0,9971 |
0,9978 |
1 |
|
|
|
|
|
… |
|
|
|
4 |
0,9967 |
0,9975 |
0,9981 |
1 |
|
|
|
|
… |
|
|
|
5 |
0,9969 |
0,9969 |
0,9974 |
0,9981 |
1 |
|
|
|
… |
|
|
|
6 |
0,9968 |
0,9972 |
0,9975 |
0,9981 |
0,9982 |
1 |
|
|
… |
|
|
|
7 |
0,9965 |
0,9967 |
0,9970 |
0,9974 |
0,9976 |
0,9984 |
1 |
|
… |
|
|
|
8 |
0,9956 |
0,9955 |
0,9962 |
0,9963 |
0,9966 |
0,9974 |
0,9984 |
1 |
… |
|
|
|
9 |
0,9951 |
0,9953 |
0,9959 |
0,9961 |
0,9960 |
0,9971 |
0,9975 |
0,9981 |
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
M-1 |
0,9883 |
0,9888 |
0,9891 |
0,9896 |
0,9894 |
0,9906 |
0,9914 |
0,9918 |
… |
1 |
|
|
M |
0,9871 |
0,9878 |
0,9879 |
0,9885 |
0,9882 |
0,9895 |
0,9907 |
0,9911 |
… |
0,9987 |
1 |
Таблица 4 - Корреляционная матрица 
, рассчитанная для массива 
по столбцам при наличии
ВЦ
|
№ ст. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
M-1 |
M |
|
1 |
1 |
|
|
|
|
|
|
|
… |
|
|
|
2 |
0,9982 |
1 |
|
|
|
|
|
|
… |
|
|
|
3 |
0,9971 |
0,9978 |
1 |
|
|
|
|
|
… |
|
|
|
4 |
0,9967 |
0,9975 |
0,9981 |
1 |
|
|
|
|
… |
|
|
|
5 |
0,9969 |
0,9969 |
0,9974 |
0,9981 |
1 |
|
|
|
… |
|
|
|
6 |
0,9855 |
0,9862 |
0,9873 |
0,9882 |
0,9873 |
1 |
|
|
… |
|
|
|
7 |
0,9965 |
0,9967 |
0,9970 |
0,9974 |
0,9976 |
0,9872 |
1 |
|
… |
|
|
|
8 |
0,9956 |
0,9955 |
0,9962 |
0,9963 |
0,9966 |
0,9873 |
0,9984 |
1 |
… |
|
|
|
9 |
0,9951 |
0,9953 |
0,9959 |
0,9961 |
0,9960 |
0,9870 |
0,9975 |
0,9981 |
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
M-1 |
0,9883 |
0,9888 |
0,9891 |
0,9896 |
0,9894 |
0,9802 |
0,9914 |
0,9918 |
… |
1 |
|
|
M |
0,9871 |
0,9878 |
0,9879 |
0,9885 |
0,9882 |
0,9792 |
0,9907 |
0,9911 |
… |
0,9987 |
1 |
|
Таблица
5 -
Вектор |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
Таблица
6 -
Вектор |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
Таблица
7 -
Вектор |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
|
Таблица 8 - Вектор налчии ВЦ |
||||||||||||||||||||||||
|
, полученный из второй диагонали корреляционной матрицы 
, рассчитанной по массиву 
, полученный из второй диагонали корреляционной матрицы 
, рассчитанной по массиву 
, полученный из второй диагонали корреляционной матрицы 
, рассчитанной по массиву 
, полученный из второй диагонали корреляционной матрицы 
, рассчитанной по массиву 
Таблица 9 - Массив 
при отсутствии ВЦ
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
M-1 |
|
1 |
0,8241 |
0,8238 |
0,8240 |
0,8240 |
0,8241 |
0,8243 |
0,8243 |
0,8240 |
… |
0,8245 |
|
2 |
0,8588 |
0,8584 |
0,8587 |
0,8587 |
0,8588 |
0,8589 |
0,8589 |
0,8587 |
… |
0,8592 |
|
3 |
0,8441 |
0,8437 |
0,8440 |
0,8440 |
0,8441 |
0,8442 |
0,8442 |
0,8440 |
… |
0,8445 |
|
4 |
0,8519 |
0,8515 |
0,8518 |
0,8518 |
0,8519 |
0,8520 |
0,8520 |
0,8518 |
… |
0,8523 |
|
5 |
0,8548 |
0,8544 |
0,8547 |
0,8547 |
0,8548 |
0,8549 |
0,8549 |
0,8547 |
… |
0,8552 |
|
6 |
0,8487 |
0,8483 |
0,8486 |
0,8486 |
0,8487 |
0,8488 |
0,8488 |
0,8486 |
… |
0,8491 |
|
7 |
0,8426 |
0,8422 |
0,8425 |
0,8425 |
0,8426 |
0,8427 |
0,8427 |
0,8425 |
… |
0,8430 |
|
8 |
0,8602 |
0,8599 |
0,8602 |
0,8602 |
0,8602 |
0,8604 |
0,8604 |
0,8602 |
… |
0,8607 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
N-1 |
0,8573 |
0,8569 |
0,8572 |
0,8572 |
0,8573 |
0,8574 |
0,8574 |
0,8572 |
… |
0,8577 |
Таблица 10 - Массив 
при наличии ВЦ
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
M-1 |
|
1 |
0,8241 |
0,8238 |
0,8240 |
0,8240 |
0,8151 |
0,8150 |
0,8243 |
0,8240 |
… |
0,8245 |
|
2 |
0,8588 |
0,8584 |
0,8587 |
0,8587 |
0,8494 |
0,8493 |
0,8589 |
0,8587 |
… |
0,8592 |
|
3 |
0,8441 |
0,8437 |
0,8440 |
0,8440 |
0,8349 |
0,8348 |
0,8442 |
0,8440 |
… |
0,8445 |
|
4 |
0,5153 |
0,5151 |
0,5152 |
0,5152 |
0,5096 |
0,5096 |
0,5154 |
0,5152 |
… |
0,5155 |
|
5 |
0,5242 |
0,5239 |
0,5241 |
0,5241 |
0,5184 |
0,5184 |
0,5243 |
0,5241 |
… |
0,5244 |
|
6 |
0,8487 |
0,8483 |
0,8486 |
0,8486 |
0,8394 |
0,8393 |
0,8488 |
0,8486 |
… |
0,8491 |
|
7 |
0,8426 |
0,8422 |
0,8425 |
0,8425 |
0,8334 |
0,8333 |
0,8427 |
0,8425 |
… |
0,8430 |
|
8 |
0,8602 |
0,8599 |
0,8602 |
0,8602 |
0,8509 |
0,8508 |
0,8604 |
0,8602 |
… |
0,8607 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
N-1 |
0,8573 |
0,8569 |
0,8572 |
0,8572 |
0,8479 |
0,8478 |
0,8574 |
0,8572 |
… |
0,8577 |
Полученные вектора 
, 
были использованы для
получения массивов 
, в каждый элемент, имеющий индексы n и m, которого записывался
результат умножения в соответствии с формулой 
, где 
и 
- величины n-го и
m-го элементов векторов 
и 
соответственно.
Примерные виды массивов 
, полученные для случаев наличия и отсутствия ВЦ,
представлены в таблицах 11, 12.
В соответствии с решающим
правилом в элемент 
записывали 1, если в
соответствующем элементе массива 
. В элемент 
записывали 0, если в
соответствующем элементе массива 
. Таким образом, окончательно сформировали массив принятия решения 
. Фрагменты массива 
при отсутствии
отметки от ВЦ представлен в таблице 11, а фрагмент массива 
с отфильтрованной
отметкой от ВЦ, представлен в таблице 12.
Таблица 11 - Массив 
на выходе порогового
устройства при отсутствии ВЦ
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
M-1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
N-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
Таблица 12 - Массив 
на выходе порогового
устройства при наличии ВЦ
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
… |
M-1 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
4 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
… |
0 |
|
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
N-1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
Массив 
был использован для
создания фоноцелевого изображения на мониторе видеоприемного устройства. Для
этого прямоугольный экран монитора видеоконтрольного устройства делили на
прямоугольные ячейки по числу строк и столбцов массива 
. Ячейки 
, содержащие нулевые значения, выделяли цветом, имеющим наибольшую
контрастность по отношению к фону экрана монитора. Считали, что в элементах
массива со значениями 
находились отметки
ВЦ. По номерам строк и столбцов элементов, отличающихся по цвету от фона экрана
монитора, определяли пространственное положение цели в сегменте полусферы
поиска. Изображение теплокадра на мониторе ВКУ с отфильтрованной отметкой ВЦ
представлено на рисунок 12, б.
Литература
1.
Жендарев М. В. Корреляционный способ обнаружения тепловых объектов
теплопеленгаторами на атмосферном фоне. ВА ВПВО ВС РФ. г. Смоленск. Вестник войсковой
ПВО. Выпуск №1. 2009. Стр. 91-94.
2. Жендарев М. В., Бирюков С.И.
Разработка математического обеспечения для проведения натурных измерений
собственных излучений воздушных целей в инфракрасном диапазоне длин волн.
Статья. Конкурс молодых ученых Смоленской области, 2009.
3. Жендарев М. В., Якименко И. В. , и
др. Способ селекции тепловых объектов. г. Москва. Федеральная служба по интеллектуальной
собственности, патентам и товарным знакам (Роспатент), Федеральный институт
промышленной собственности. Заявка на изобретение (регистрационный №
2008143830).
4. Дьяконов В. П. Энциклопедия Mathcad
2001i, 11. Библиотека профессионала. М.: Солон-Пресс.- 2004.- 832 с.
5. Дьяконов В. П. Mathcad 8-12 для
студентов. М.: СОЛОН-Пресс.- 2005.
6. Дьяконов В. П. Mathcad 11/12/13 в
математике. Справочник. М. Горячая линия. Телеком. – 2007.
ALGORITHM to TWO-DIMENSIONAL
SPATIAL FILTERING DESIGNED ON BASE KORRELYACIONNOGO MEDIA COVERAGE of the
BACKGROUND
Zhendarev M.V.
On the basis of correlation way is developed the algorithm of the bidimentional spatial filter which can be realized programmatically in the video processor of the heat direction finder. The algorithm allows automating process of the air targets detection (planes, helicopters, cruise missiles, unpiloted aircraft, etc.) and to provide the display of their video images to the monitor of the video control device in the binary kind.
Key word: correlation way, algorithm
of the bidimentional spatial filter.
Кафедра радиотехники
Академия
войсковой ПВО Вооруженных Сил РФ
им.
Маршала Советского Союза А. М. Василевского, г. Смоленск
Поступила в редакцию 18.11.2009.