Математическая морфология.
Электронный математический и
медико-биологический журнал. - Т. 9. -
Вып. 1. - 2010. - URL:
http://www.smolensk.ru/user/sgma/MMORPH/TITL.HTM
http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/TITL-25.htm
http://www.smolensk.ru/user/sgma/MMORPH/N-25-html/cont.htm
УДК 517.927
Краевая задача
общей структуры для системы ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
© 2010 г. Исраилов С. В. Сагитов А. А.
В работе ставится и изучается
краевая задача новой структуры для системы обыкновенных дифференциальных
уравнений, из которой получаются при некоторых значениях присутствующих
параметров многие известные и ранее исследованные задачи (Коши, Валле Пуссена,
Николетти и др.). Приводится две теоремы о существовании и единственности
решения, полученных путем преобразования данной задачи и другим задачам.
Ключевые слова: краевая задача общей структуры, линейные отображения,
эквивалентные краевые задачи, существование и единственность решения.
1. Задача
для системы обыкновенных дифференциальных уравнений (ОДУ)
, (1)
с
краевыми условиями
, (2)
сформулированная
в области 
, где 
, данные числа, 
,как для непрерывных правых частей 
, по совокупности аргументов, так и для сингулярных по
независимый переменный 
и по фазовым координатам 
, изучена многими авторами и называется по разному: задача
Николетти 
, задача не типа Коши 
, задача Коши-Николетти 
и т.д. Различные ее
вариации рассматривались и для функционально-дифференциальных и дифференциально-алгебраических
систем. Получены достаточно тонкие признаки существования и единственности решения
.
Множество неразрешенных проблем, в
эпицентре которых оказалась Чечня в годы русско-чеченской смуты, в моем
сознании ассоциировалась со сложными задачами для системы ОДУ с многоточечными
краевыми условиями ранее неизученных структур, над которыми размышлял, чтобы отвлечься
от реальной действительности, в холодных подвалах разрушенных домов Грозного
военных зим 1994-1995, 1999-2000 годов под грохот артобстрелов, ракетных атак и
бомбежек. В то же время более сложную задачу спасения чеченского народа решал
политик А.Кадыров, позже первый президент Чечни. Его памяти и посвящается
скромные результаты изысканий тех времен по разрешимости специальной
многоточечной граничной задачи для системы (1) с условиями:
, (3)
где
Для наглядного обозрения расшифруем
структуру (3) и запишем их в равносильном виде:
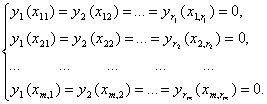(4)
Из-за равенства 
при 
имеем 
и в равенствах (4)
остается только первая строка, означающая условие задачи Николетти, т.е. при 
задача (1), (3) совпадает с задачей Николетти (1), (2), если
положить 
в частности, когда 
, получаем задачу Коши.
Если в (3) или (4) одно или несколько
из чисел 
равняется нулю, то из
условий (4) выпадают строки, соответствующие им; при 
из равенства 
следует 
в случае 
, и имеем задачу Вале-Пуссена 
При 
имеем 
и если ни одно из
чисел 
не равняется нулю, то
в равенствах (4) остаются только первые
две строки, при 
получается 
и если 
то в условиях (4) остается только первые три строки и т.д.
Таким образом, придавая различные
натуральные числовые значения 
и комбинируя числами 
из граничных условий (3), получаем как ранее изученные
краевые задачи, так и краевые задачи новых типов, что подтверждает
оригинальность и неповторимость задачи (1), (3), как граничной задач наиболее
общей структуры для системы ОДУ с охватом большого количества точек из сегмента
.
Дальнейшее содержание работы касается
разрешимости задачи, единственности решения и метода их получения.
2.
Обозначим через 
- множества п-мерных
вектор-функций с непрерывно-дифференцируемыми
элементами на 
множество матриц из п-строк
и п-столбцов с
непрерывно-дифференцируемыми элементами
на 
.
Вектор-функция 
называется решением
задачи (1), (3), если она удовлетворяет системе (1) и граничным условиям (3).
В дальнейшем будем считать, что функции
, непрерывны по совокупности аргументов в области D и для
любых векторов 
имеет место условие
Липшица.
, (5)
где
-пространство непрерывных векторов – функций.
Пусть задана матрица 
такая, что
(6)
. (7)
Рассмотрим вектор-функцию 
числовые значения
которой при 
не выходят из области 
:
, где 
-некоторые числа, о которых будут специальные оговорки.
Установим между вектор-функциями 
и 
соответственно со
значениями из области 
и 
взаимно-однозначное соответствие с помощью линейных равенств:
, (8)
что
вполне возможно из-за (6). Обозначим
, (9)
и
будем считать, что числа 
и 
таковы, что выполняется неравенства
. (10)
Тогда
равенства (8) отображают числовые значения вектор-функции 
в область 
.
Пусть вектор-функция 
удовлетворяет
условиям (3). Тогда вектор функция 
будет удовлетворят условиям
, (11)
где
, (12)
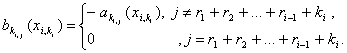(13)
Считая функции 
, из (9) решением
системы (1), построим относительно функций 
, систему ОДУ:
, (14)
где
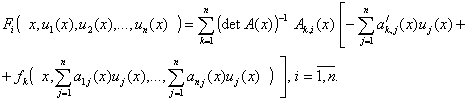(15)
Здесь 
-алгебраические дополнения элементов матрицы 
.
Для любых векторов 
из области 
с учетом (5) из (15) получим:
, (16)
где
, (17)
Возьмем подмножество 
вектор-функций 
со значениями из области 
. Нетрудно проверить, что в подмножестве 
краевая задача (14),
(11) эквивалентны системе интегральных уравнений.
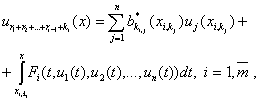(18)
.
Для ясности
распишем систему (18): при 
имеем 
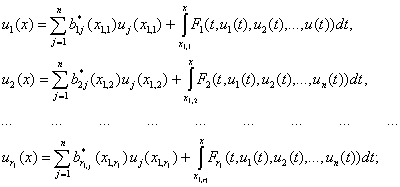
(19)
при
имеем:
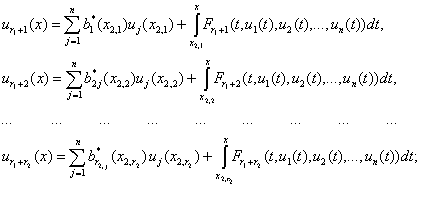(20)
и
т.д. при 
получим:
,
,
… … … … … … … … … … … …
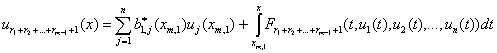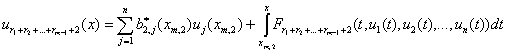(21)
.
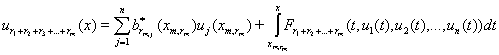Если
положить
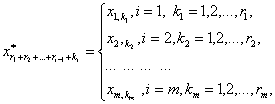
то
система нагруженных интегральных уравнений (19)-(21) запишется в компактном
виде
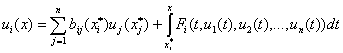, (21)
,
, т.е имеем систему из
n-нагруженных интегральных уравнений.
3.
Наряду с системой (21) рассмотрим еще систему
, 
.
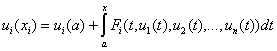(22)
Найдем
, 
, так, чтобы системы (21), (22) совпали,
для
этого в (22) положим 
, 
, и полученное выражение
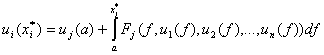(23)
подставим
в (21):
, 
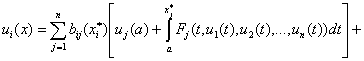
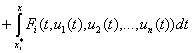. (24)
При
из (24) имеем
, 
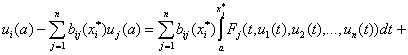
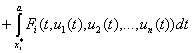(25)
или
алгебраическо - функциональную систему
, 
, (26)
где
через 
обозначены правые
части системы (25) и
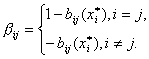
Будем
считать, что матрица 
такова, что
(27)
Из
(26) находим
, 
(28)
и
систему (22) перепишем в виде
, 
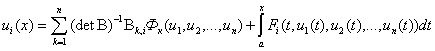, (29)
где
- алгебраические дополнения элементов матрицы 
.
Интегральную систему (29) будем изучать в подмножестве
.
Функции
ограничены в области D из-за их непрерывности, поэтому
, 
,
(30)
где
- некоторые числа. Функции 
, 
, обладают такими же свойствами, что и у функции 
и элементы матрицы 
в области D
и так же ограничены
некоторыми числами 
:
, 
. (31)
Тогда
функционалы 
оцениваются просто в
той же области D
:
, 
, (32)
и
в свою очередь можно оценить функции 
из (29):
, 
. (33)
Теперь,
если предположить
, 
. (34)
то
интегральные операторы в правых частях (29) отображают множества 
в себя. Взяв соответствующую норму в пространстве 
, по схеме, не раз примененной в монографии 
. доказывается полная непрерывность интегральных операторов
из правых частей, что обеспечивает существование решения задачи (14), (11).
Поэтому по методу построения системы (14) с краевыми условиями (11) путем
использования матрицы 
из линейных
преобразований (8) с привлечением системы (1) и краевых условий (3) следует,
что любое решение задачи 
приводит к решению 
задачи (1),(3) в силу равенств (8).
Пусть задача (14),(11) имеет два
решения 
. Из (29) получим оценки:
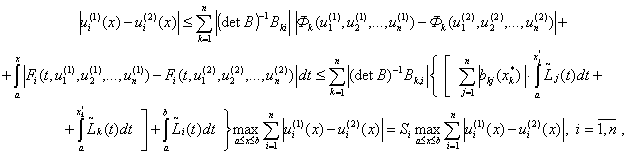(35)
где
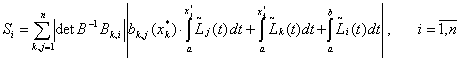. (36)
Суммируя
левые и правые части неравенств (36), получим:
(37)
и
при
(38)
решение
будет единственным.
4.
Может случится, что неравенство (27) не
выполняется и тогда система (21) не переводится в систему (29). В этом случае в
множестве
рассматривают непосредственно саму систему (21) с ее
нагруженными правыми частями и на числа 
из области 
налагаются
дополнительные ограничения в виде неравенств:
где
, обеспечивающие отображения правыми частями (21) множества 
в себя, после чего можно применить один из методов, предложенных для доказательства
теорем существования и единственности в монографии 
.
Таким
образом, доказаны две теоремы:
Т
е о р е м а 1. Для разрешимости задачи (1),(3) необходимо и достаточно, чтобы
была разрешима задачи (14),(11).
Т
е о р е м а 2. При перечисленных допущениях относительно правых частей 
и матрицы 
задача (1),(3) имеет
решение, причем единственное.
Литература
1.
Nicoletti О Sulle condizioni
iniziali che determiniano gli integrali della diffenziali ordinazie – Att della
R. Acc. Sc. Torino. 1897, 1898. 748-759.
2.
Найшуль А.Б. Решение
системы обыкновенных дифференциальных уравнений с начальными данными не типа
Коши //Доклад АН СССР. 1949. Т.67. №6. С-969-972
3.
Исраилов С.В. О
сингулярной многоточечной краевой
задаче //Уч. записки Азербайджанского госуниверситета. Серия ф-м. науки 1963.
№3. С. 63-71.
4.
Кигурадзе И.Т. Некоторые
сингулярные краевые задачи для обыкновенных дифференциальных уравнений.
Издательство Тбилисского университета, 1975.
5.
Исраилов С.В., Юшаев
С.С. Многоточечные и функциональные краевые
задачи для обыкновенных дифференциальных уравнений. Нальчик, издательский центр
«Эльфа». 2004. С.445.
6.
Исраилов С.В.
Многоточечная краевая задача Коши-Николетти для системы дифференциальных уравнений с запаздывающим аргументом и
некоторые вопросы колеблемости решений
// Издательство Северокавказского научного центра высшей школы. Естественные
науки. 1974. №4. С.72-76.
7.
Ешуков Л.Н., Веков А.А.,
Степанов Л.Н. Проблемы и библиография теории краевых задач обыкновенных
дифференциальных уравнений // Тр. Рязанского радиотехнического института. 1979.
Вып. 42. С. 164-192.
8.
Васильев Н.И., Клоков
Ю.А. Основы теории краевых задач обыкновенных дифференциальных уравнений. Рига:
Зинетне, 1978. С.184.
Boundary value problem of
generic structure for ordinary differential equation system
Israilov S.V., Sagitov A. A.
In this work there is set and studied boundary value problem of new structure for singular differential
equations system from which comes out at some values of present parameters many
known and earlier investigated solutions (Cauchy, de la Vallee-Poussin,
Nickoletti, etc.) is put and studied. There is shown two theorems of existence
and uniqueness of the solution which are received by transformation of the
given problem and other problems.
Keywords: boundary
value problem of generic structure, linear mapping, equivalent boundary
value problem, existence and uniqueness of the solution.
Домашний адрес:
364000, г.Грозный , поселок Калинина, улица Дарвина № 67, Исраилов Сейдахмед Вахидович.
Исраилов Сейдахмед Вахидович, профессор кафедры «Алгебра и геометрия» Чеченского государственного университета
Darvin Street, 67
Kalinina Settlement
Grozny / 364 000 / Israilov Seidakhmed
Vakhidovich
Тел. Моб.: 89284766402.
Электронный адрес: segitov@mail.ru
Israilov Seidakhmed Vakhaevich, professor of
"Algebra and Geometry Department" of the Che chen State University
Домашний адрес:
366701, Чеченская Республика, Сунженский район, станица Серноводская, улица Наги Асуева №79,
Сагитов Адам Аюпович
Электронный адрес:segitov@mail .ru
Homeaddress: Chechen Republic. Naggi Asueva Street, 79
Sernjvodskaya District Sungenski Region 366 701
E-mail:
segitov@mail.ru
Кафедра алгебры и геометрии
Чеченский государственный
университет
г. Грозный
Поступила в редакцию 23.03.2010.